Тригонометрические функции, их свойства и графики. Периодичность тригонометрических функций

1. Тригонометрические функции, их свойства и графики. Периодичность тригонометрических функций. Понятие обратной функции, ее

свойства.

2.

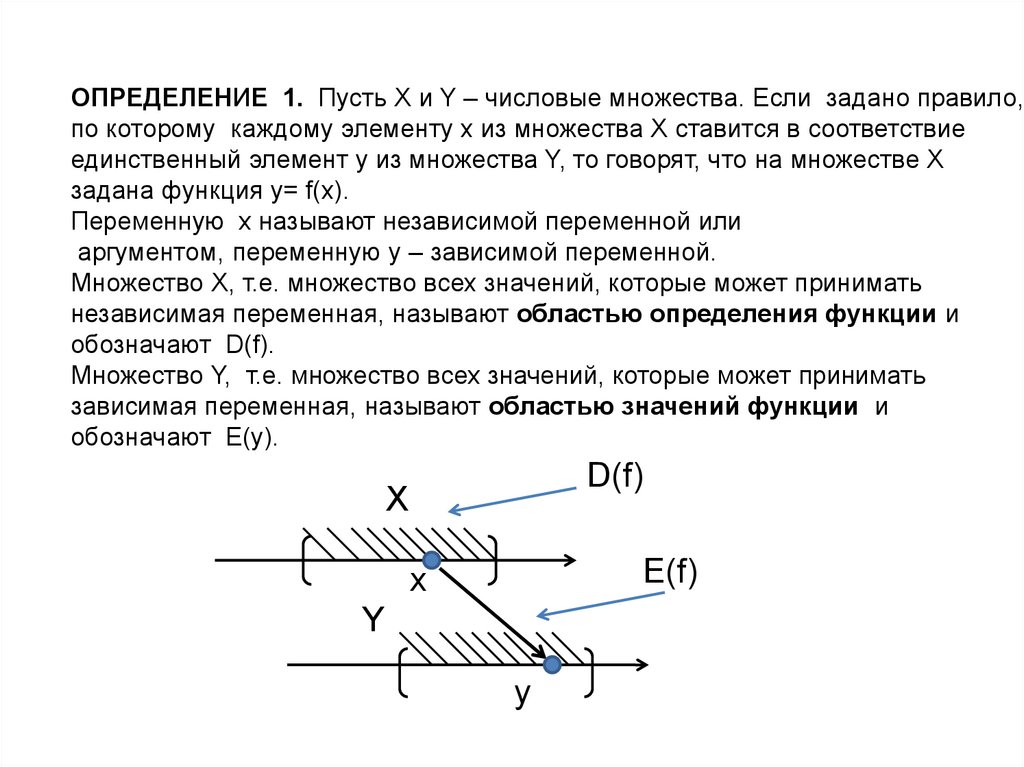
ОПРЕДЕЛЕНИЕ 1. Пусть X и Y – числовые множества. Если задано правило,
по которому каждому элементу х из множества Х ставится в соответствие
единственный элемент y из множества Y, то говорят, что на множестве Х
задана функция y= f(x).
Переменную х называют независимой переменной или
аргументом, переменную у – зависимой переменной.
Множество Х, т.е. множество всех значений, которые может принимать
независимая переменная, называют областью определения функции и
обозначают D(f).
Множество Y, т.е. множество всех значений, которые может принимать
зависимая переменная, называют областью значений функции и
обозначают E(y).
D(f)
X
E(f)
x
Y
y

3.

ОПРЕДЕЛЕНИЕ 2. Функция y = f(x) называется четной, если ее область
определения симметрична относительно 0 и для любого значения х из
области определения выполняется равенство f(- x) = f(x).
Функция y = f(x) называется нечетной, если ее область
определения симметрична относительно 0 и для любого значения х из
области определения выполняется равенство f(- x) = - f(x)
График четной функции симметричен относительно оси Оу.
График нечетной функции симметричен относительно начала координат,
т.е. относительно точки (0; 0).
Верно и обратное: если график функции симметричен относительно оси
Оу, то функция четная,
если график симметричен относительно начала координат,
то функция нечетная.

4.

ОПРЕДЕЛЕНИЕ 3. Функция y = f(x) называется возрастающей на
промежутке Р, принадлежащим области определения функции, если
для любых значений аргумента х1 и х2 из промежутка Р, таких, что х1 < х2
выполняется неравенство f(х1) < f(х2 ).
Функция y = f(x) называется убывающей на промежутке Р,
принадлежащим области определения функции, если для любых
значений аргумента х1 и х2 из промежутка Р, таких, что х1 < х2
выполняется неравенство f(х1) > f(х2 ).
Функция y = f(x) называется неубывающей на промежутке Р,
принадлежащим области определения функции, если для любых
значений аргумента х1 и х2 из промежутка Р, таких, что х1 < х2
выполняется неравенство f(х1) ≤ f(х2 ).
Функция y = f(x) называется невозрастающей на промежутке Р,
принадлежащим области определения функции, если для любых
значений аргумента х1 и х2 из промежутка Р, таких, что х1 < х2
выполняется неравенство f(х1) ≥ f(х2 ).
Функция называется возрастающей, если она возрастает на всей
области определения. Функция называется убывающей, если она
убывает на всей области определения.

5.

ОПРЕДЕЛЕНИЕ 4. Функция y = f(x) называется
ограниченной снизу, если существует число m, такое, что
f(x) ≥ m для всех значений аргумента х из области
определения функции.
Функция y = f(x) называется ограниченной сверху, если
существует число М, такое, что f(x) ≤ М для всех значений
аргумента х из области определения функции.
Если функция ограничена и сверху, и снизу, то ее называют
ограниченной
ОПРЕДЕЛЕНИЕ 5. Нули функции – это значения аргумента, при которых
Функция обращается в 0.
На графике это абсциссы точек пересечения с осью Ох.

6.

Определение. Говорят, что функция у = f (x) имеет период Т,
если для любого х ϵ D(f) числа х + Т и х – Т также принадлежат
D(f) и при этом выполняется равенство
f(x – T) = f( x) = f(x + T)
Определение. Функцию, имеющую отличный от нуля период Т,
называют периодической.
Если функция имеет период Т, то любое число кратное Т
(т.е. число вида кТ, к ϵ Z) также является ее периодом.
Наименьший положительный период называют основным
периодом

7.

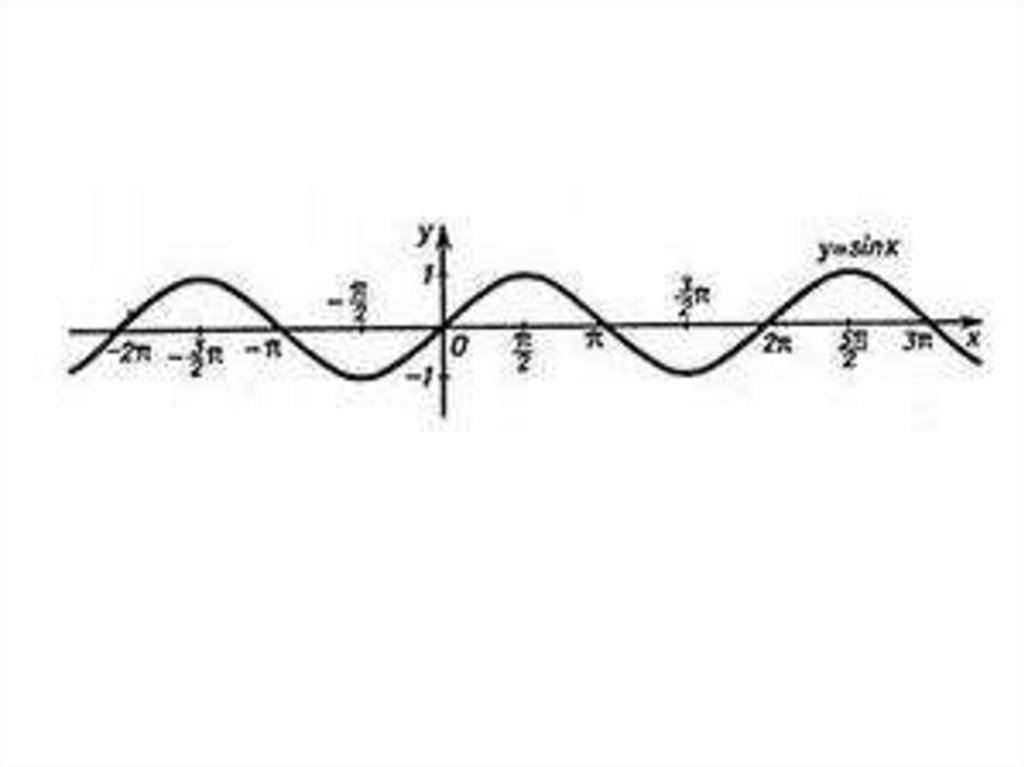
Функция y = sin x, ее свойства и
график

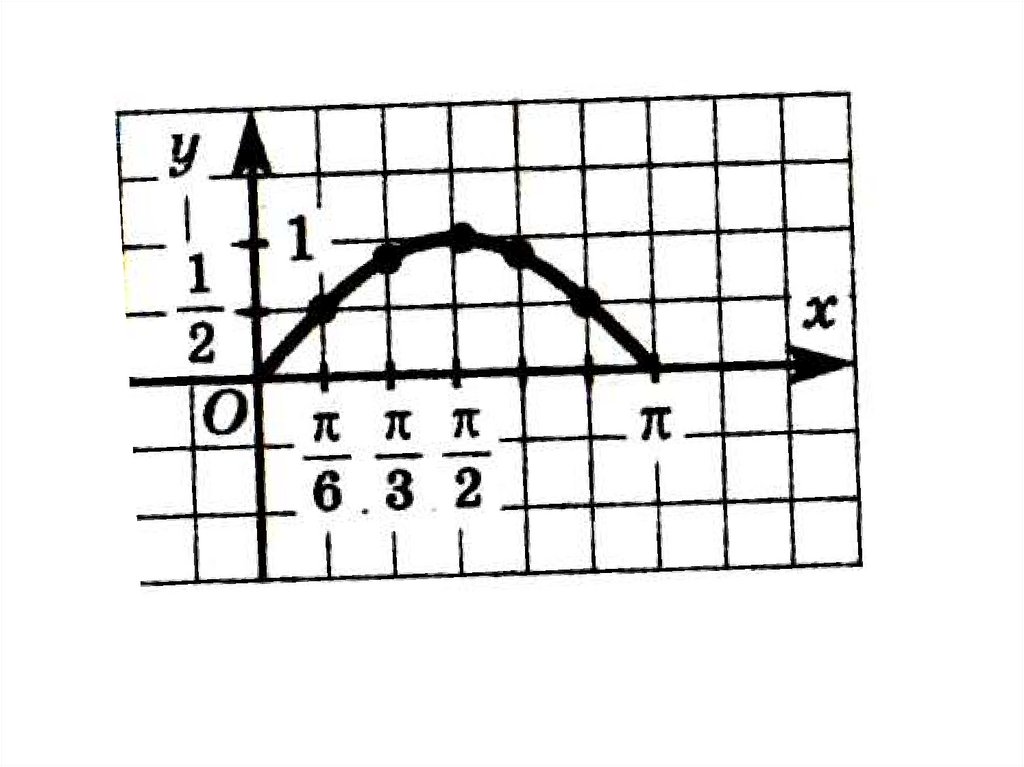
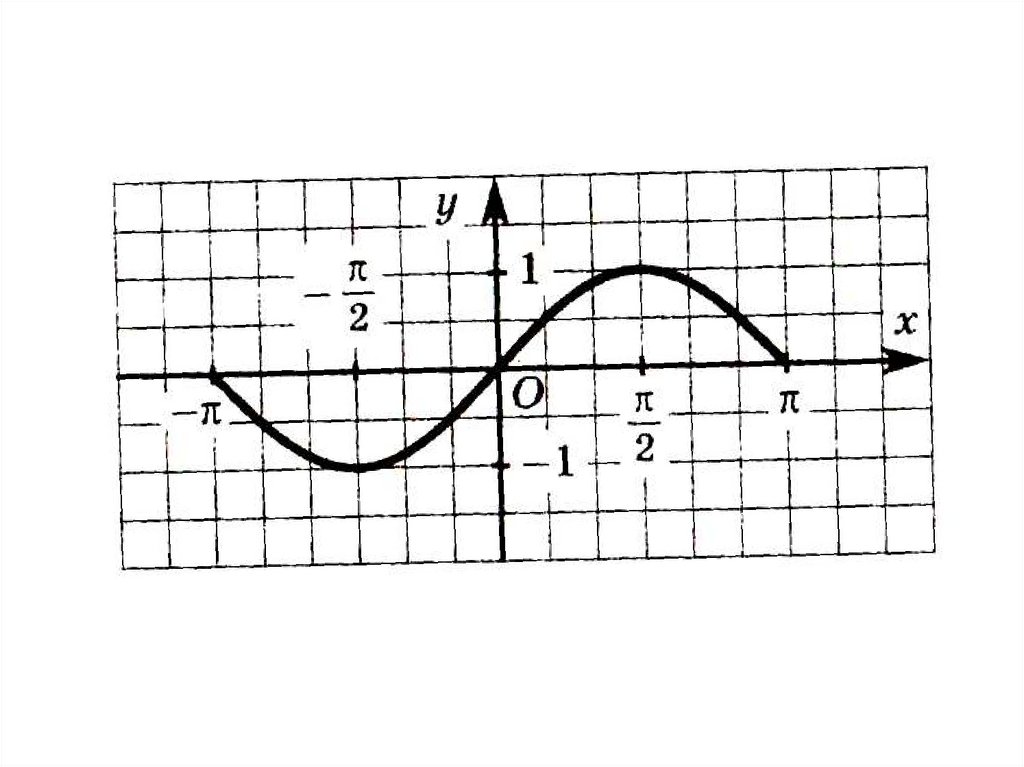
8.

1. D(sin) = ( - ∞; + ∞)
2. Функция у = sin x нечетная: sin( х) sin х
3. Нули функции
x k , k Z
4. Функция периодическая, основной период 2π
5. Функция возрастает на любом отрезке
2 2 k ; 2 2 k , k Z
вида
и убывает на любом отрезке вида
3
2
k
;
2
k
, k Z
2
2

9.

6. Функция ограничена снизу и сверху
1 sin х 1
7. Наименьшее значение yнаим. 1
достигается при
х
2
2 k , k Z
Наибольшее значение унаиб. 1
достигается при
х
2
2 k , k Z

10.

8. Функция y = sin x - непрерывная функция
9. Область значений
Е(sin)=[-1; 1]

11.

12.

13.

14.

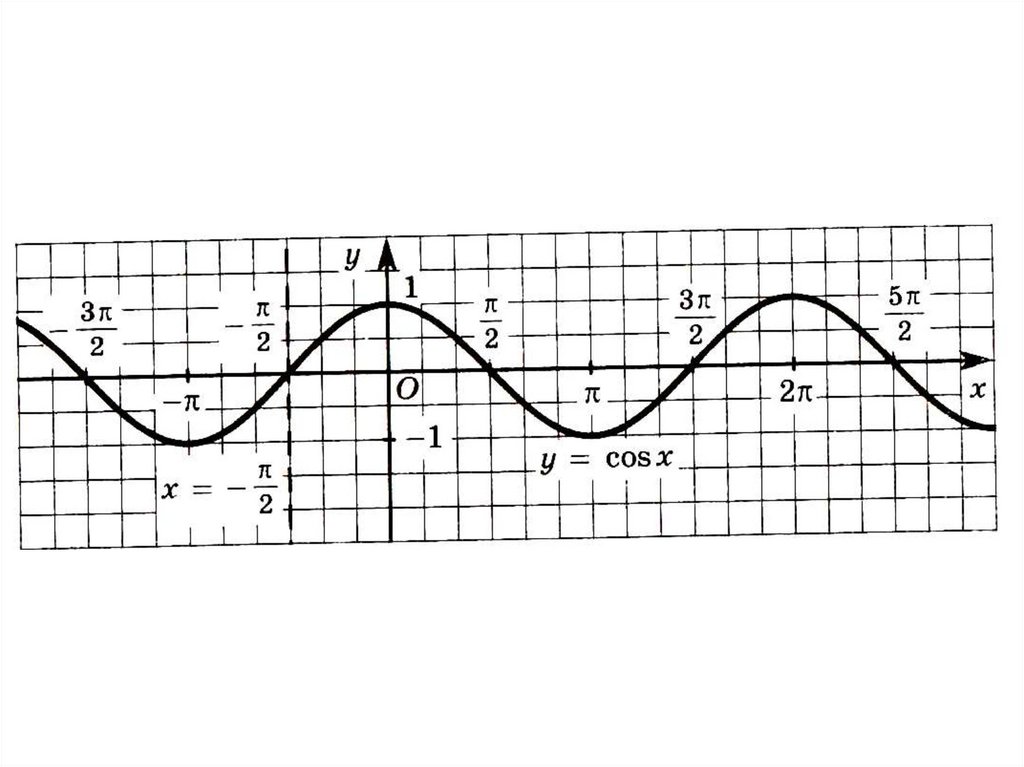
Функция y = cos x, ее свойства и
график

15.

cos х sin(
2
x)

16.

17.

1. D(cos) = ( - ∞; + ∞)
2. Функция у = cos x четная cos( х) cos x
3. Нули функции
x
2
k , k Z
4. Функция периодическая.
Основной период равен 2π.

18.

5. Функция возрастает на любом отрезке
вида 2 k; 2 2 k , k Z
и убывает на любом отрезке вида
0 2 k; 2 k , k Z

19.

6. Функция ограничена снизу и сверху
1 cos х 1
7. Наименьшее значение
достигается при
yнаим. 1
х 2 k , k Z
Наибольшее значение унаиб. 1
достигается при
х 2 k , k Z

20.

8. Функция y = cos x - непрерывная функция
9. Область значений функции y = cos x:
Е(cos)=[-1; 1]

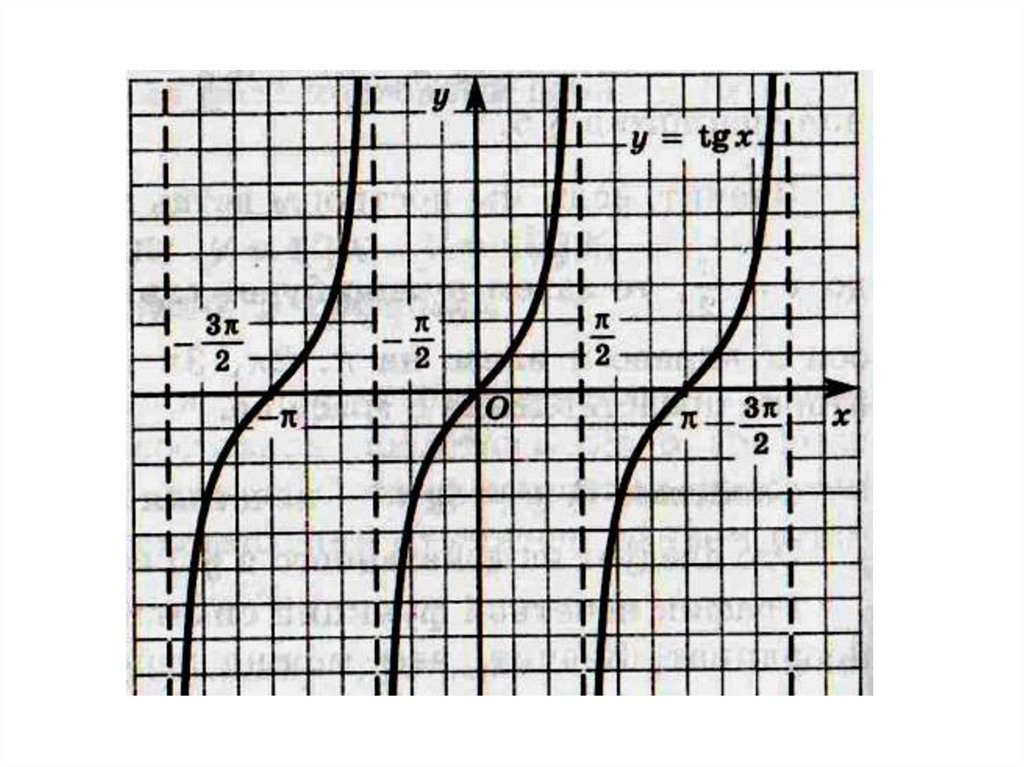
21. Функции y = tg x, y = ctg x, их свойства и графики

22.

Свойства функции y = tg x
1. D(tg): x k , k Z
2
2. Функция у = tg x нечетная. График
симметричен относительно начала координат
tg ( х) tg x
3. Функция у = tg x периодическая.
Основной период равен π
tg ( x ) tg x tg ( x )
4. Нули функции
x k , k Z

23.

5. Функция возрастает на любом интервале
вида
k ; k , k Z
2
2
6. Функция y = tg x не ограничена ни снизу,
ни сверху
7. Функция y = tg x не имеет ни
наибольшего, ни наименьшего значения

24.

8. Функция y = tg x – непрерывна на любом
интервале вида k ; k , k Z
2
2
Прямые x
k , k Z
2
являются вертикальными асимптотами
9. Область значений функции y = tg x:
Е(tg) = (-∞; +∞)

25.

26.

27.

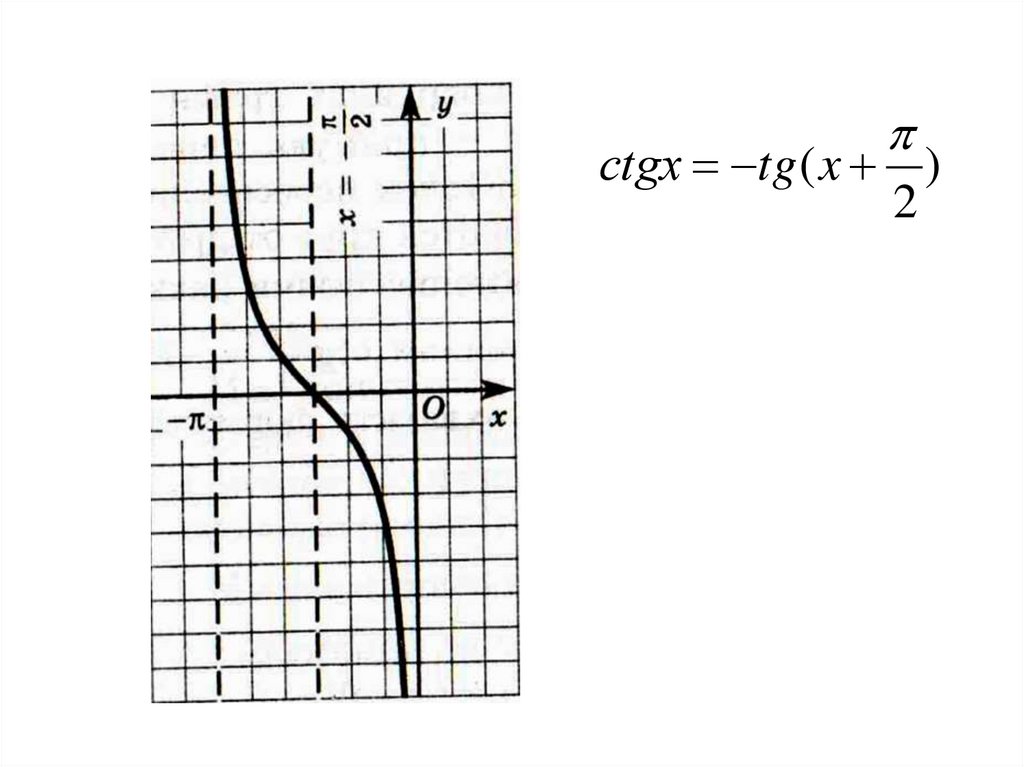
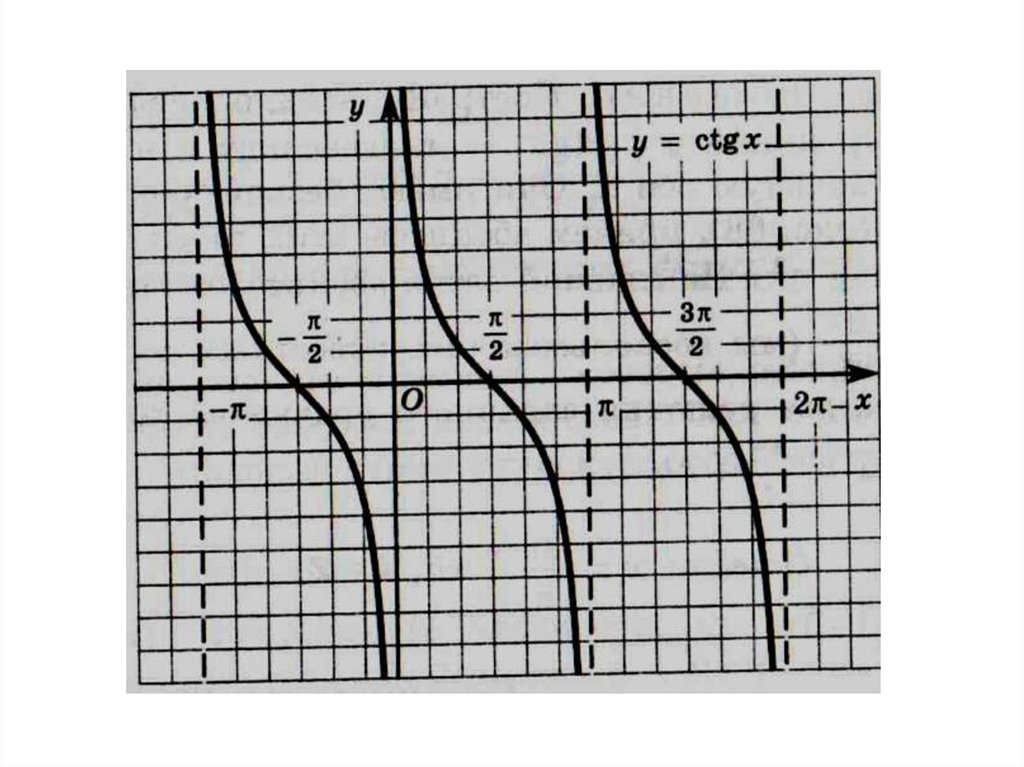
Свойства функции y = ctg x
1. D(ctg):
x k , k Z
2. Функция у = ctg x нечетная.
сtg ( х) сtg x
3. Функция у = ctg x периодическая.
Основной период равен π
сtg ( x ) сtg x сtg ( x )
4. Нули функции
x
2
k , k Z

28.

5. Функция убывает на любом интервале
вида
k; k , k Z
6. Функция y = сtg x не ограничена ни снизу,
ни сверху
7. Функция y = сtg x не имеет ни
наибольшего, ни наименьшего значения

29.

8. Функция y = сtg x – непрерывна на любом
k; k , k Z
интервале вида
Прямые
x k , k Z
являются вертикальными асимптотами
9. Область значений функции y = сtg x:
Е(сtg) = (-∞; +∞)

30.

сtgx tg ( x )
2

31.

32.

Определение. Функцию у = f (x) называют обратимой на
множестве Х, если любое свое значение она принимает только в
одной точке множества Х (т.е. разным значениям аргумента
соответствуют разные значения функции)
Теорема. Если функция y = f (x) монотонна на множестве Х,
то она обратима на Х.
Определение. Пусть обратимая функция y = f (x) определена на
множестве Х и Е(f) = Y. Поставим в соответствие каждому у ϵ Y
то единственное значение х, при котором f( x ) = y. Тогда получим
Функцию, которая определена на Y, а Х – область значений
функции. Эту функцию называют обратной к функции y = f (х ) и
обозначают y = f -1(x).
Теорема. Если функция = f(x) возрастает (убывает) на множестве
Х, а Y – область значений функции, то обратная функция
возрастает (убывает ) на Y.