Similar presentations:
Четность и нечетность тригонометрических функций
1.
Четность и нечетностьтригонометрических
функций
2. Определение:
Функция f(х) называется чётной, если длякаждого х из области определения этой
функции выполняется равенство:
f(-х)=f(х)
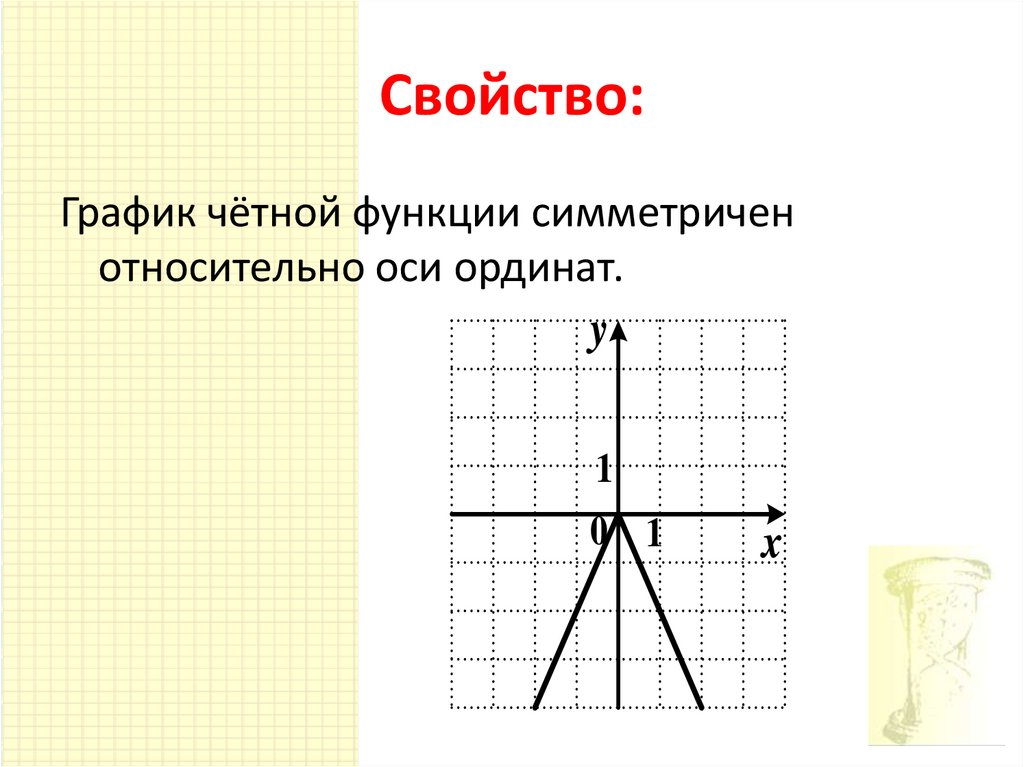
3. Свойство:
График чётной функции симметриченотносительно оси ординат.
y
1
0 1
x
4. Определение:
Функция f(х) называется нечётной, если длякаждого х из области определения этой
функции выполняется равенство:
f(-х)=-f(х)
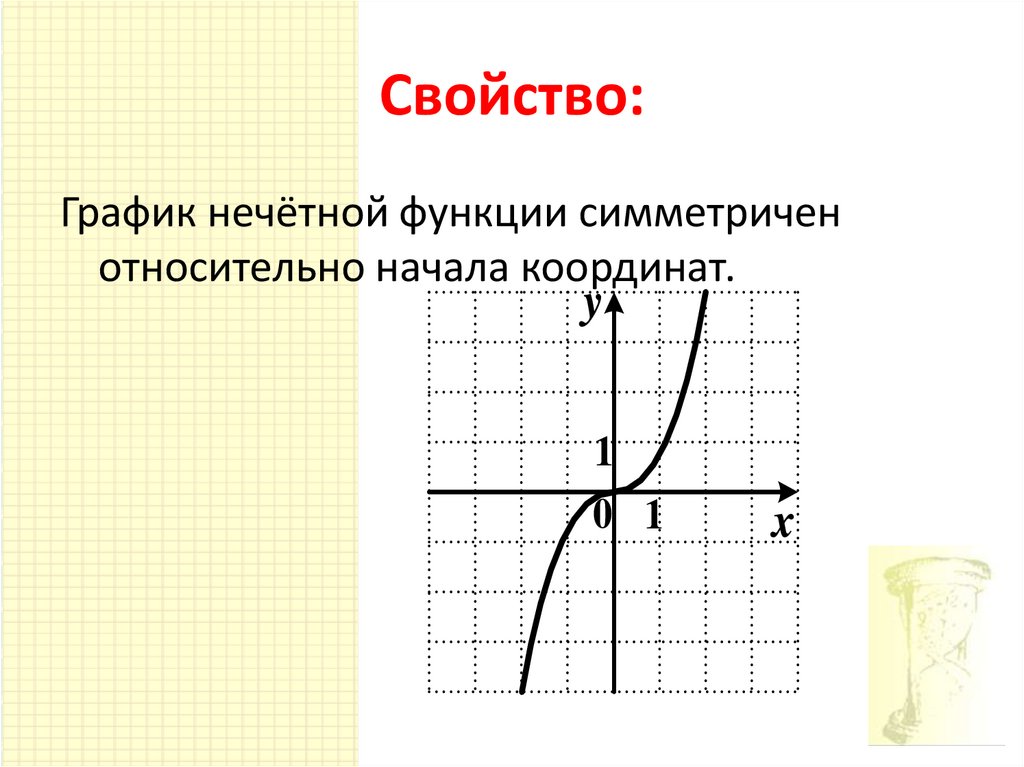
5. Свойство:
График нечётной функции симметриченотносительно начала координат.
y
1
0 1
x
6.
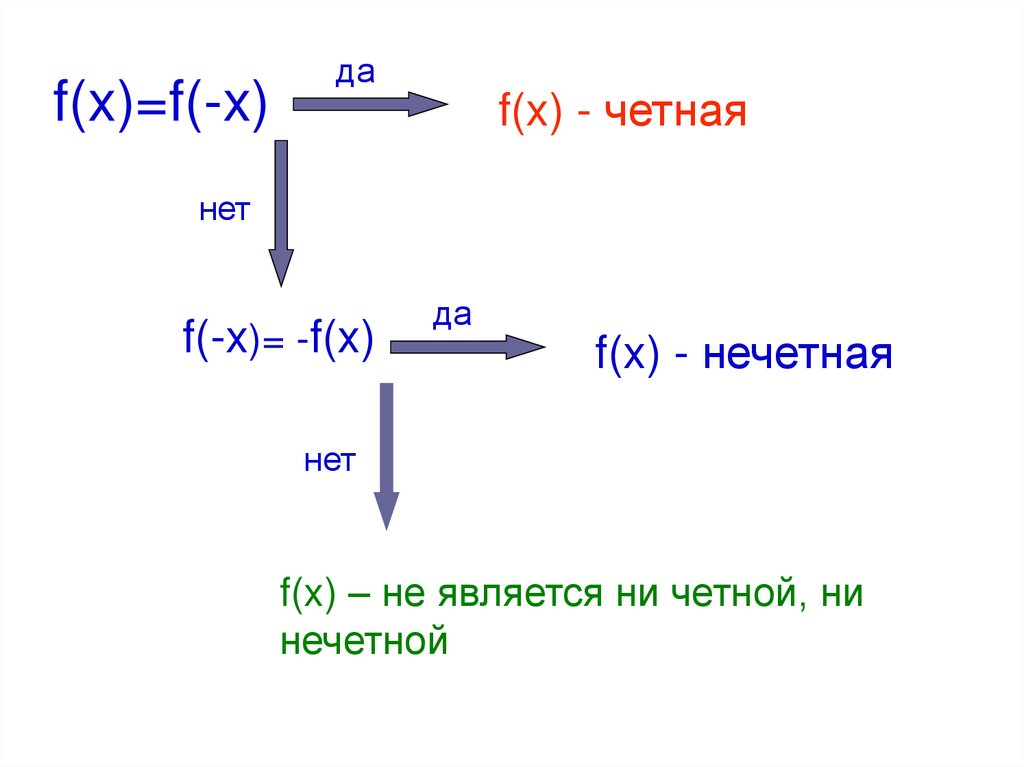
f(x)=f(-x)да
f(x) - четная
нет
f(-x)= -f(x)
да
f(x) - нечетная
нет
f(x) – не является ни четной, ни
нечетной
7.
y=f(x), x 0У
у=f(x) - четная
О
у=f(x) - нечетная
Х
8. Задание 1: Укажите график нечетной функции.
yy
1
1
0 1
x
y
1
0 1
x
0 1
x
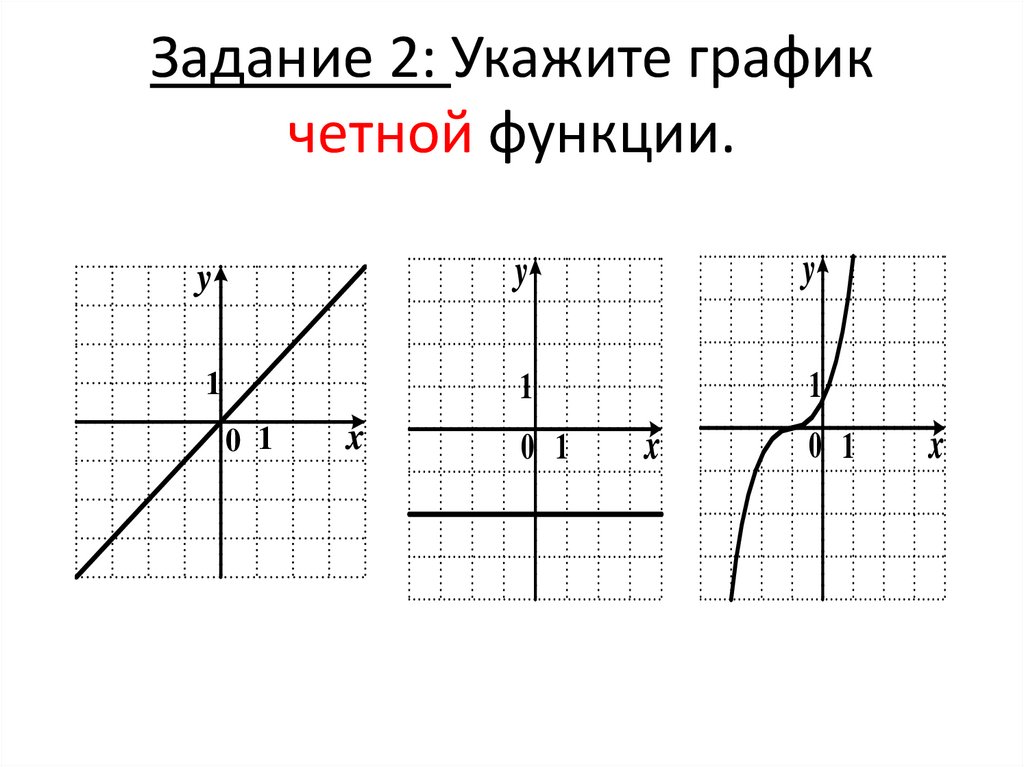
9. Задание 2: Укажите график четной функции.
yy
y
1
1
1
0 1
x
0 1
x
0 1
x
10.
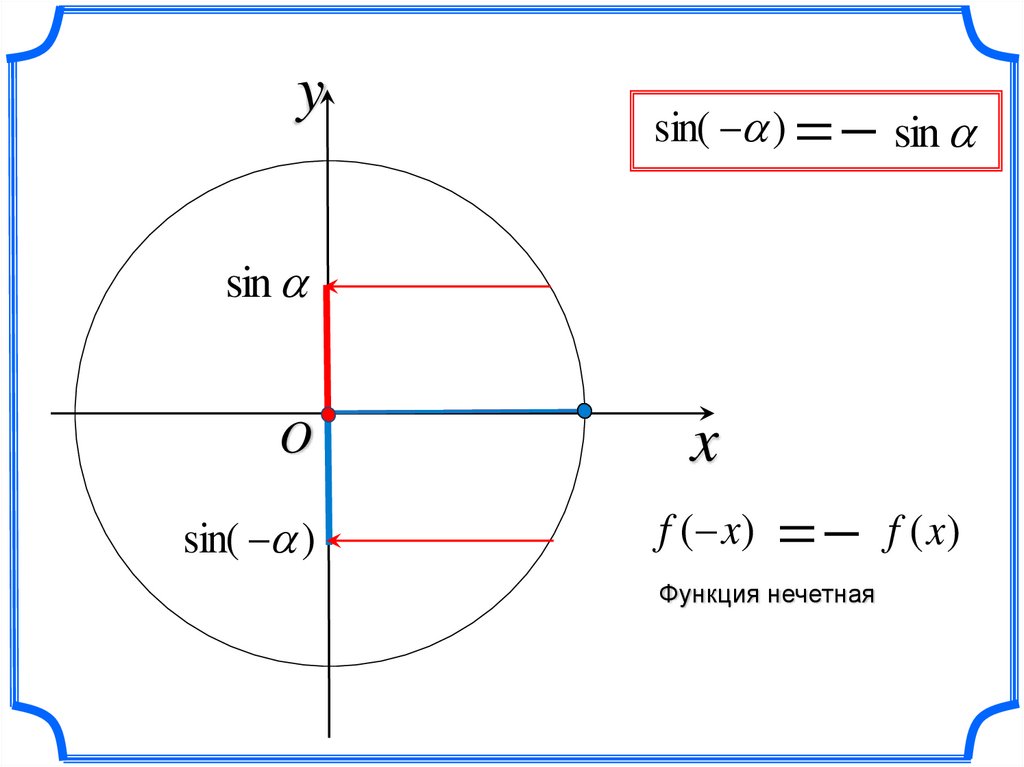
ysin( ) sin
sin
O
sin( )
x
f ( x)
Функция нечетная
f (x)
11.
ycos( )
cos
f (x)
cos
O
x
cos( )
f ( x)
Функция четная
12.
sintg
cos
sin
sin ( ) sin
tg( )
tg
cos
cos
cos( )
f ( x)
Функция нечетная
f (x)
tg( ) tg
ctg( ) ctg
13.
f ( x)f (x)
Функция четная
cos( )
f ( x)
f (x)
Функция нечетная
cos
sin( ) sin
tg( ) tg
ctg( ) ctg
14. Формулы сложения
1.sin(x + y)= sinx·cosy + siny·cosx2.cos(x + y)= cosx·cosy - sinx·siny
3.sin(x – y)= sinx·cosy - siny·cosx
4.cos(x – y)= cosx·cosy + sinx·siny
5.
6.
15. Самостоятельная работа
I вариантII вариант
Вычислить
1 4 sin( ) 2 cos( 3 ) 3ctg ( )
1
2
3
6
2
4
sin 20 cos 10 cos 20 sin 10
8
8
sin
cos sin cos
7
7
7
7
4 sin 73 cos 17 cos 73 sin 17
5 sin 7 cos sin cos 7
12
12
12
12
2
3
4
5
6 cos( ) 4 sin 7tg ( )
3
4
cos 20 cos 40 sin 20 sin 40
4
5
tg
tg
9
9
4
5
1 tg
tg
9
9
sin 73 cos17 cos 73 sin 17
5
5
sin
cos sin
cos
12
12
12
12










 mathematics
mathematics








