Свойства функции: нечетность и четность

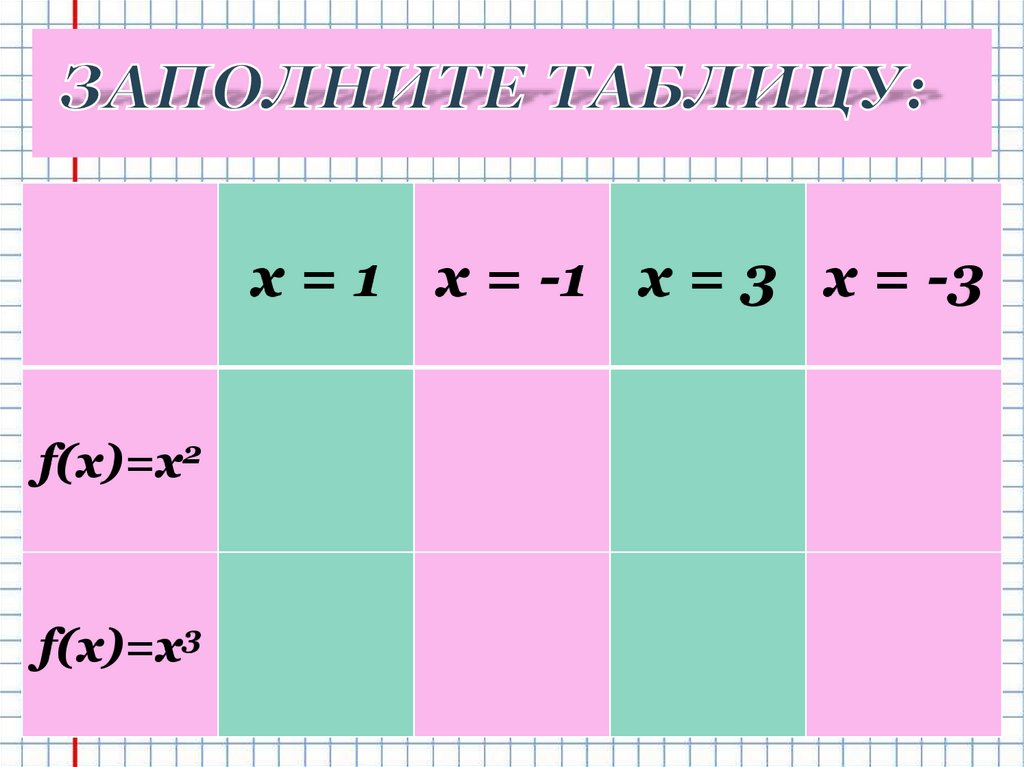
1.

x = 1 x = -1 x = 3 x = -3
f(x)=x2
f(x)=x3

2.

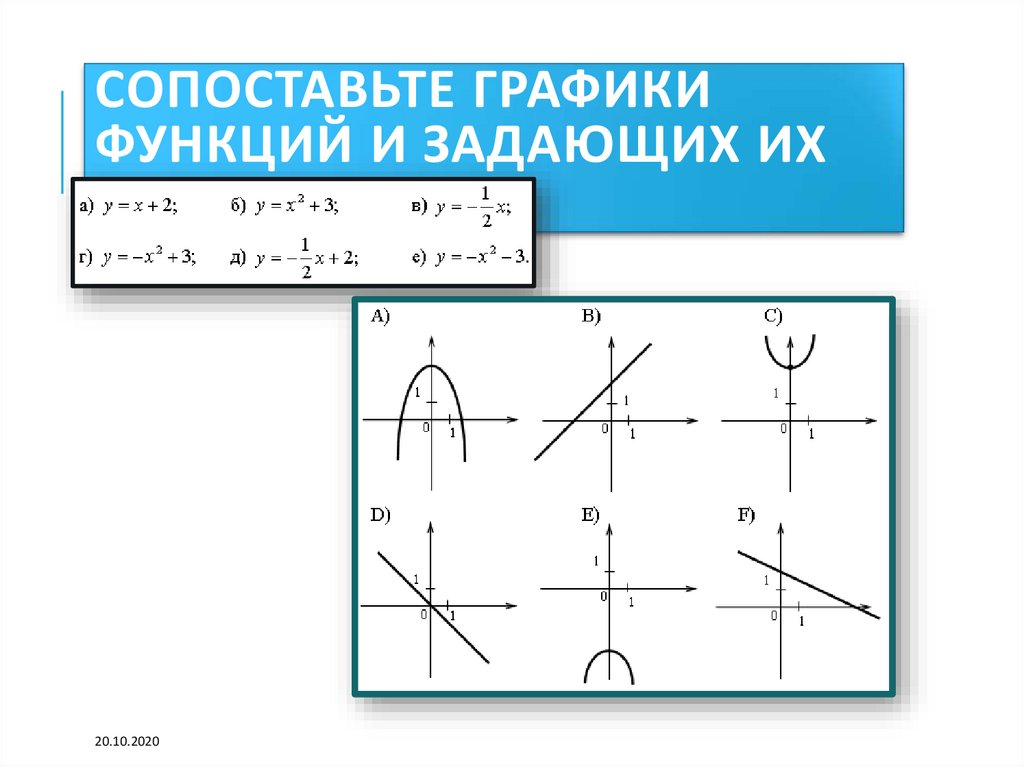
СОПОСТАВЬТЕ ГРАФИКИ
ФУНКЦИЙ И ЗАДАЮЩИХ ИХ
ФОРМУЛ.
20.10.2020

3.

НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ
ФУНКЦИИ, ЗАДАННОЙ
ФОРМУЛОЙ.
20.10.2020

4.

5.

Формирование знаний свойств четности и нечетности функций;
Выработка навыков использования четности и нечетности для
построения графиков функций.

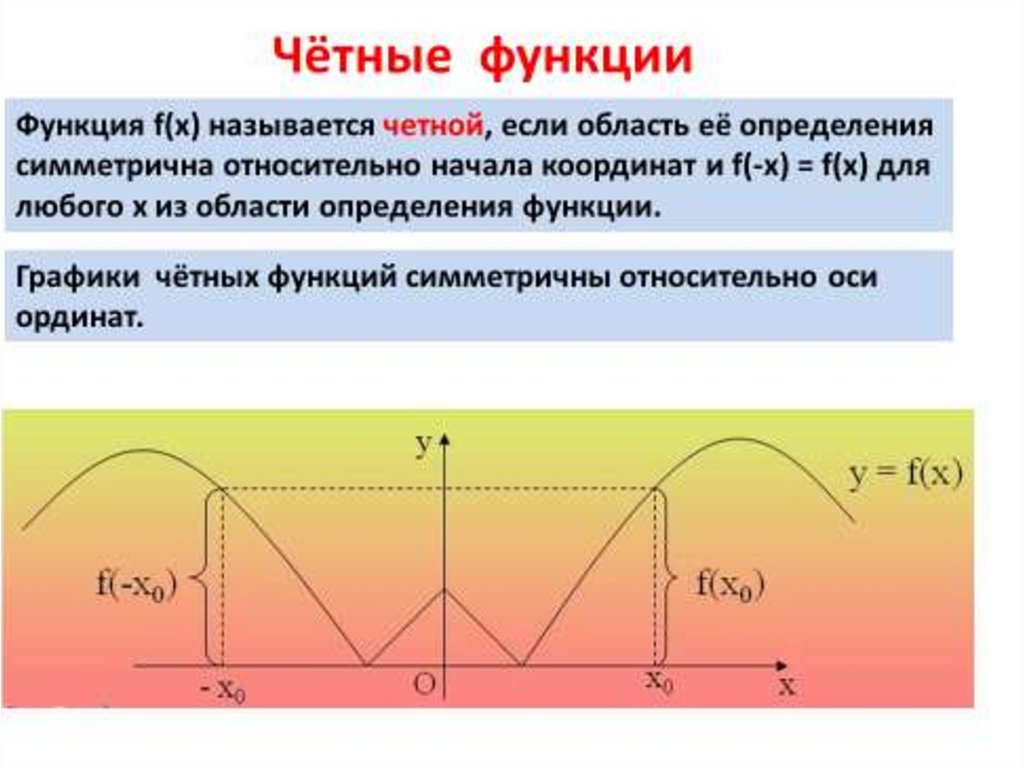
6.

7.

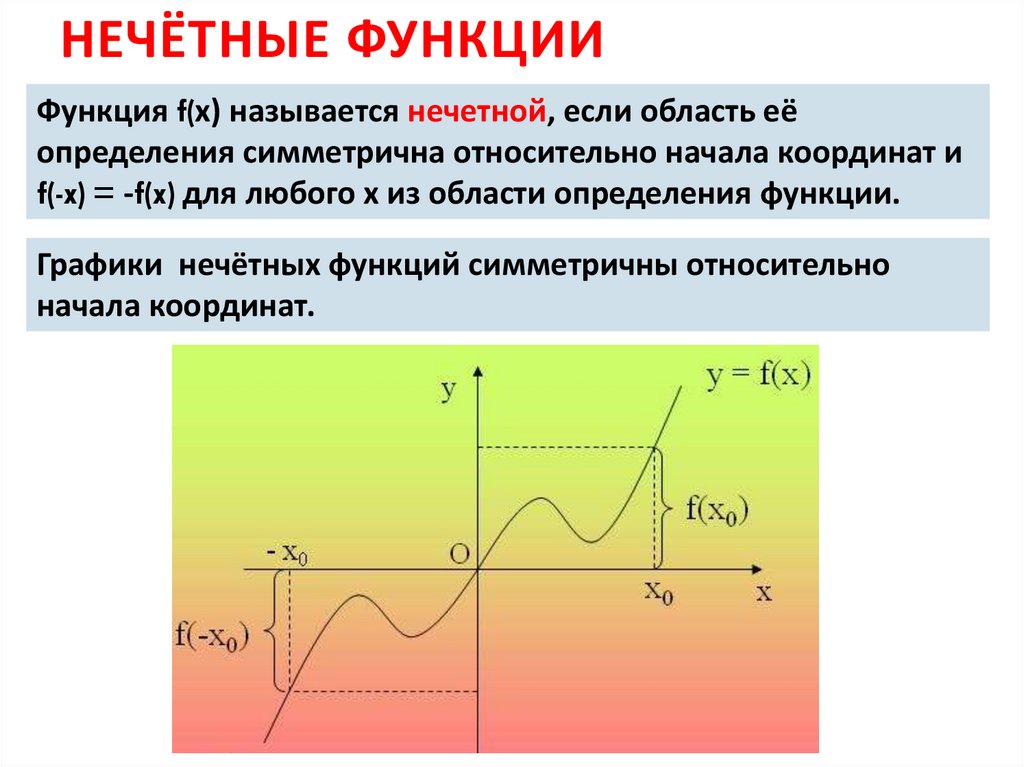
НЕЧЁТНЫЕ ФУНКЦИИ
Функция f(х) называется нечетной, если область её
определения симметрична относительно начала координат и
f(-x) = -f(x) для любого х из области определения функции.
Графики нечётных функций симметричны относительно
начала координат.

8.

Алгоритм исследования функции
на чётность.
1. Установить, симметрична ли область
определения функции. Если нет, то функция
не является ни чётной, ни нечётной. Если да,
то перейти к шагу 2 алгоритма.
2. Составить выражение для f(-х).
3. Сравнить f(-х) и f(х):
– если f(-х) = f(х), то функция чётная;
– если f(-х) = - f(х), то функция нечётная;
– если f(-х) ≠ f(х) и f(-х) ≠ - f(х), то функция не
является ни чётной, ни нечётной.

9.

Определите, являются ли заданные
множества симетричными?
А) (-2;2)
Б) (-2;2]
В)
Г)
Д) [0; ∞)
Е)

10.

Определите
среди
приведенных
множеств, те
которые
являются
симметричными.
а
б
в
г
2
-3
0
-3
0
3
x
-3
0
3
x
-3
0
3
x
д -∞
0
x
x
+∞

11.

Исследуйте функцию на
четность.
f(x)= 4х6 -х2.

12.

Исследуйте функцию на четность.
f(x)= 4х6 -х2.
Решение:
D(f)=R
f(-x)= 4·(-х)6 -(-х)2 =4х6 – х2
f(-x)=f(x).Функция четная

13.

Исследуйте функцию на четность.
f(x)= 7х5 -х3.
Решение:

14.

Исследуйте функцию на четность.
f(x)= 7х5 -х3.
Решение:
D(f)=R
f(-x)= 7·(-х)5 -(-х)3 =-7х5 + х3
=-(7x5-x3)=-f(x)
f(-x)=-f(x). Функция нечетная

15.

16.

17.

18.

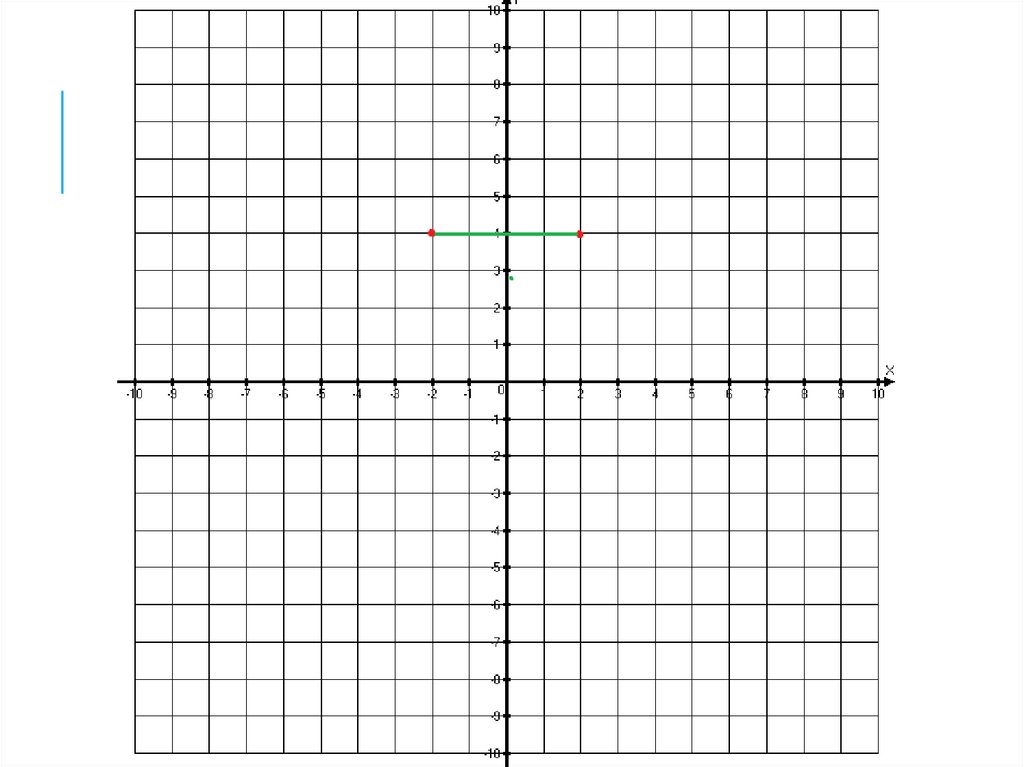
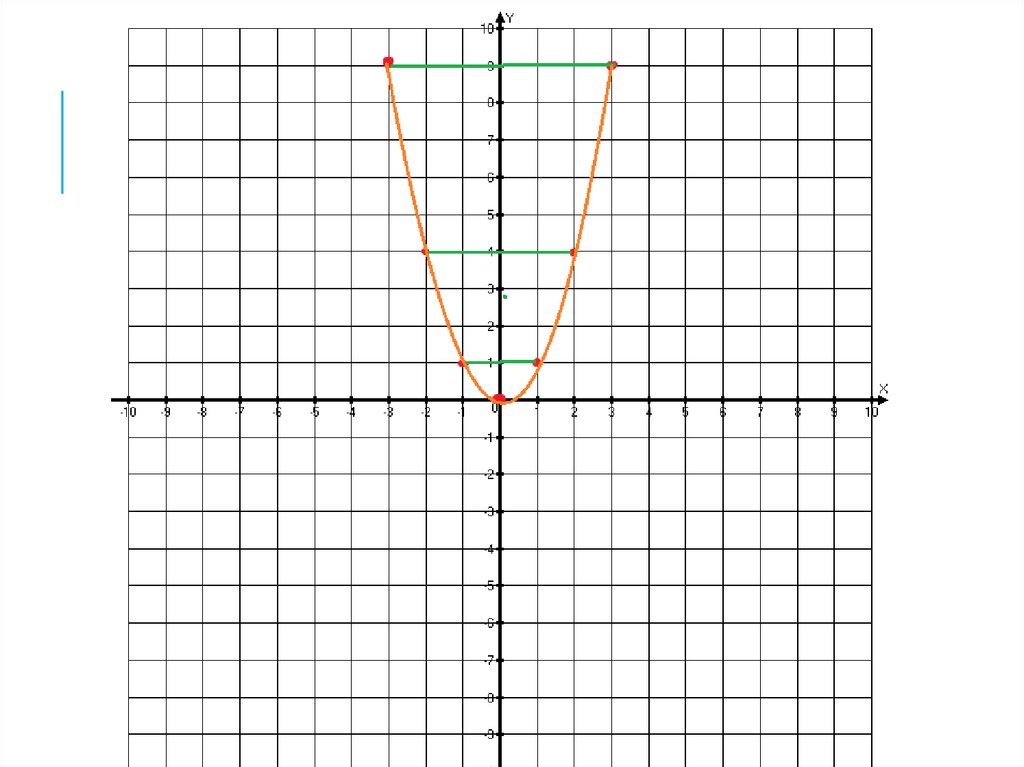
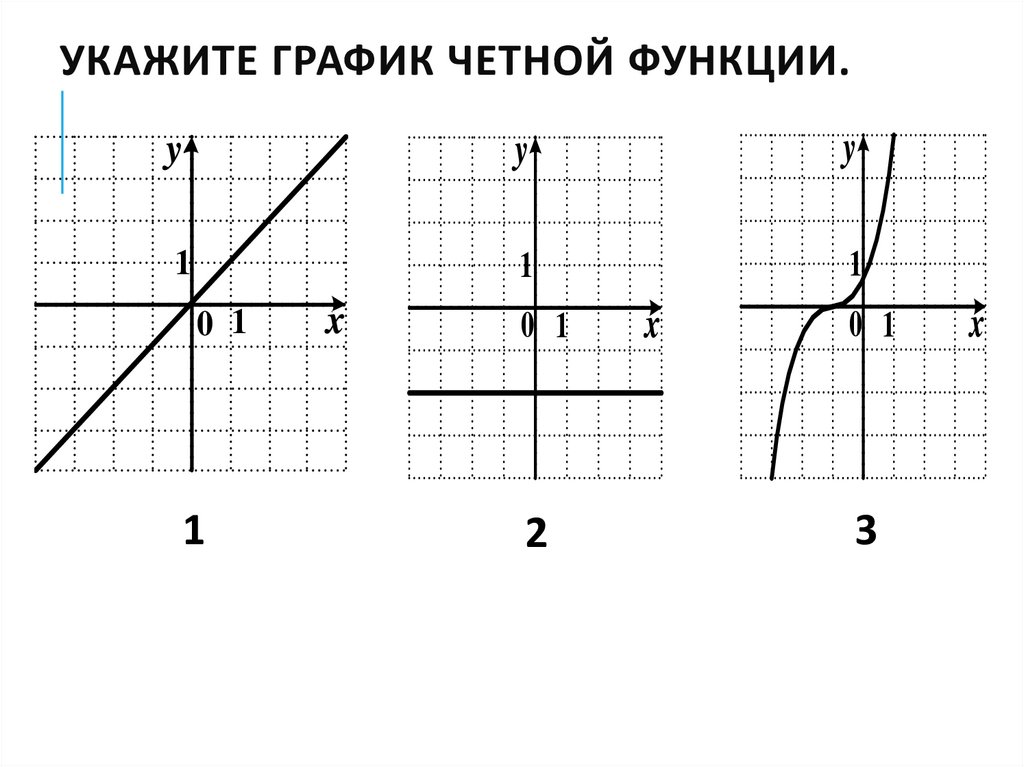
УКАЖИТЕ ГРАФИК ЧЕТНОЙ ФУНКЦИИ.
y
y
y
1
1
1
0 1
1
x
0 1
2
x
0 1
3
x

19.

УКАЖИТЕ ГРАФИК ЧЕТНОЙ
ФУНКЦИИ.
y
y
1
1
0 1
1
y
1
0 1 x
0 1
2
3
x
x

20.

21.

22.

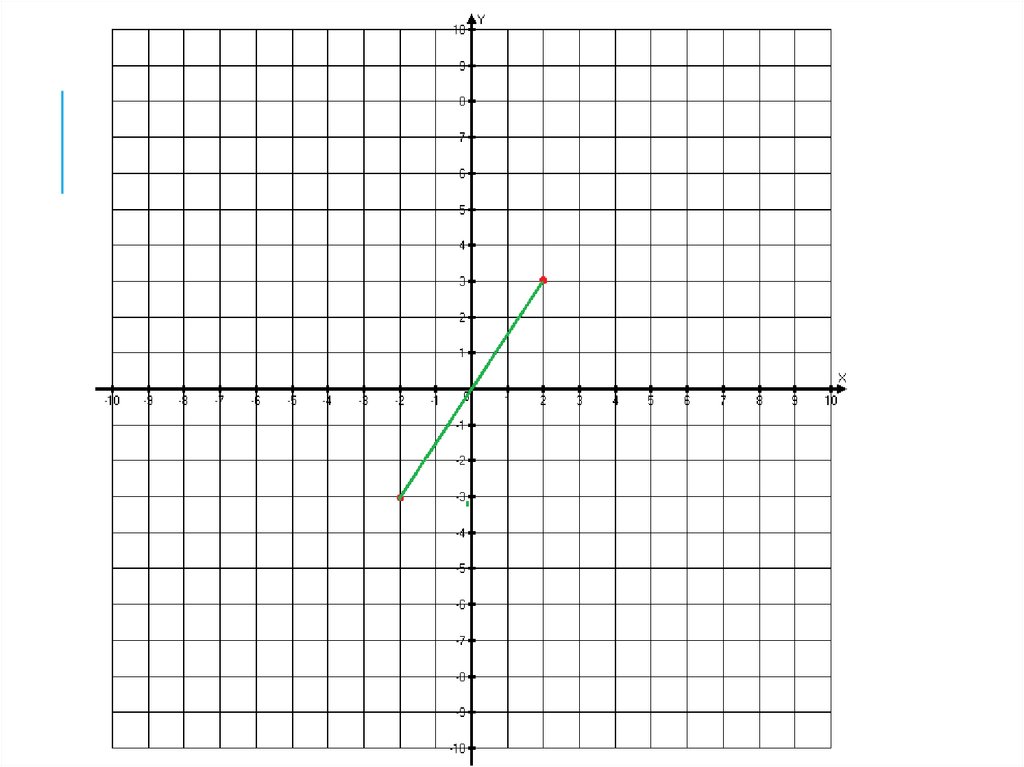
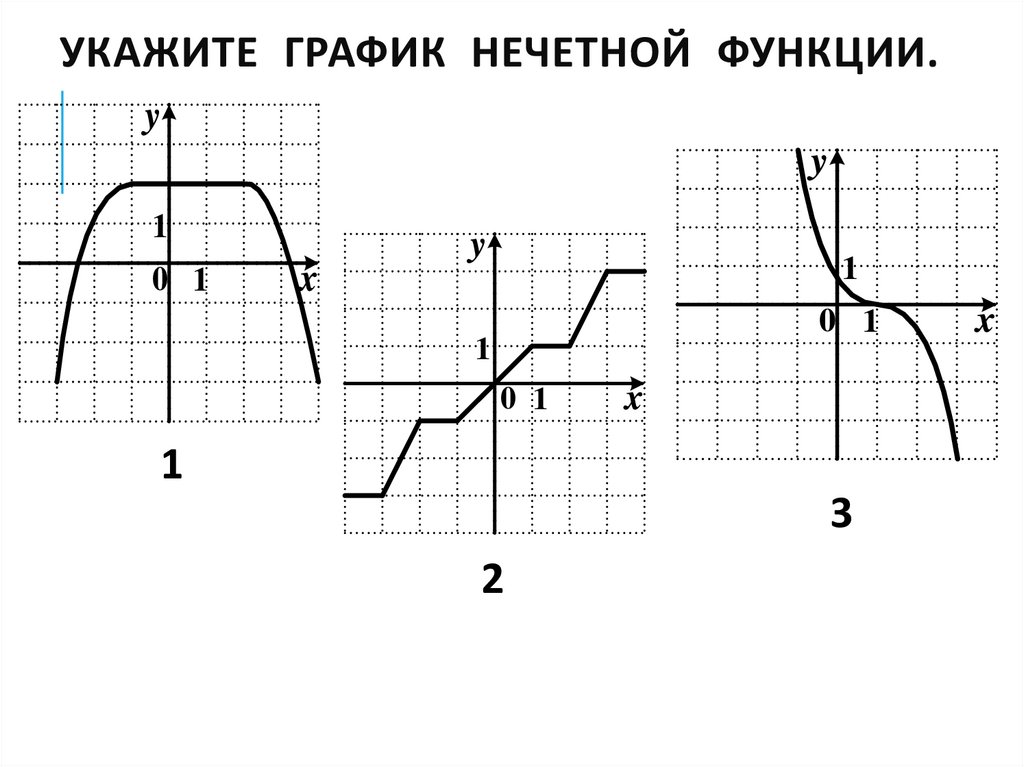
УКАЖИТЕ ГРАФИК НЕЧЕТНОЙ ФУНКЦИИ.
y
y
1
0 1
y
1
x
0 1
1
0 1
x
1
3
2
x

23.

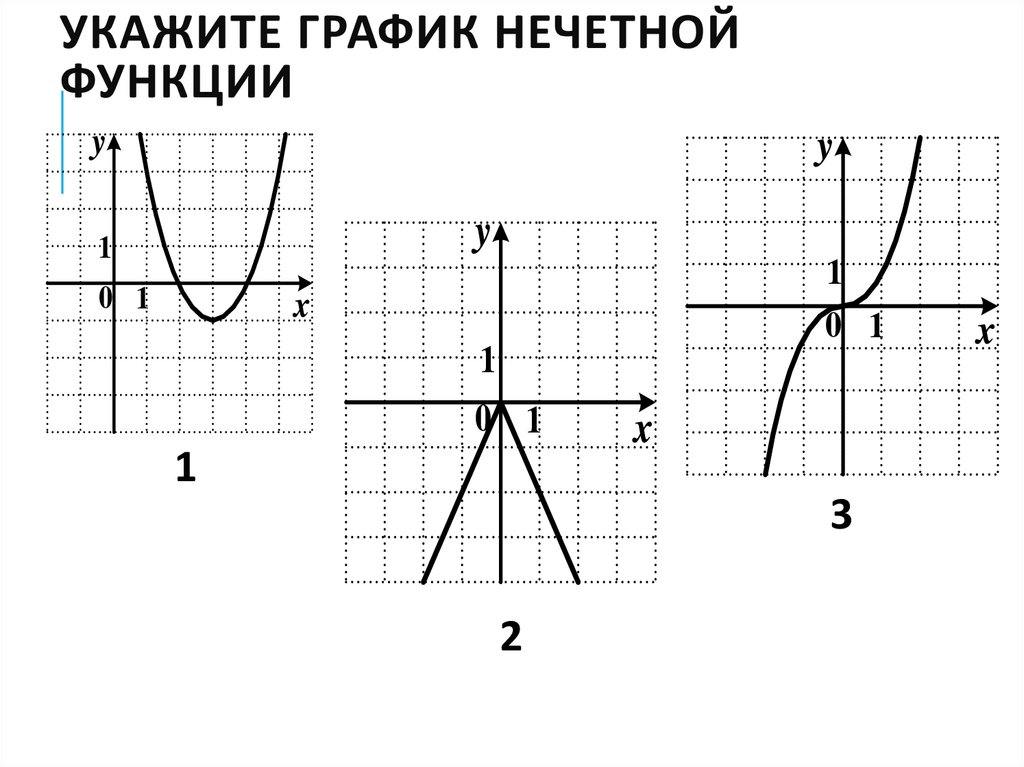
УКАЖИТЕ ГРАФИК НЕЧЕТНОЙ
ФУНКЦИИ
y
y
y
1
0 1
1
0 1
x
1
0 1
1
x
3
2
x

24.

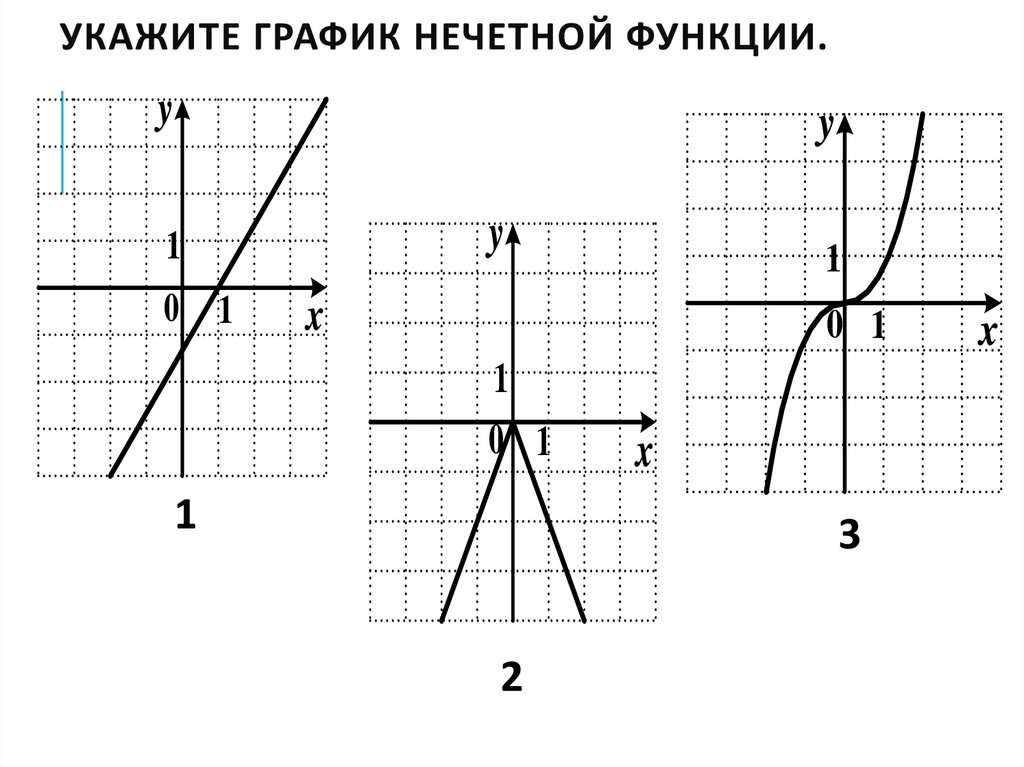
УКАЖИТЕ ГРАФИК НЕЧЕТНОЙ ФУНКЦИИ.
y
y
y
1
0 1
1
x
0 1
1
0 1
1
x
3
2
x

25.

26.

27.

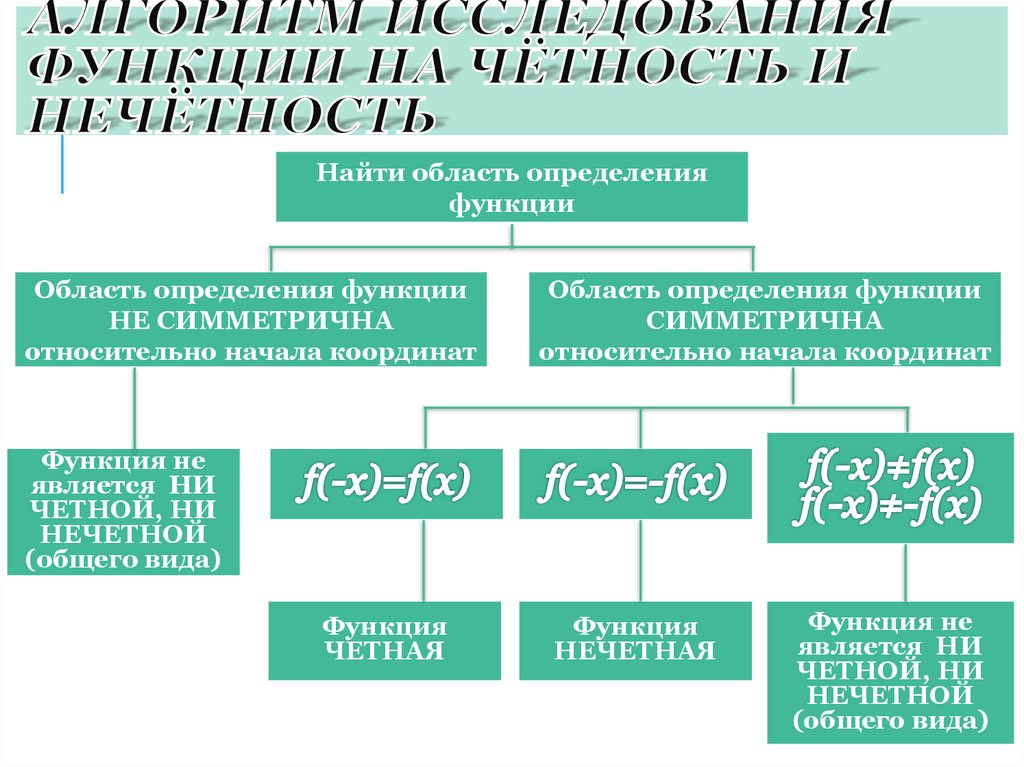
Найти область определения
функции
Область определения функции
НЕ СИММЕТРИЧНА
относительно начала координат
Область определения функции
СИММЕТРИЧНА
относительно начала координат
Функция не
является НИ
ЧЕТНОЙ, НИ
НЕЧЕТНОЙ
(общего вида)
Функция
ЧЕТНАЯ
Функция
НЕЧЕТНАЯ
Функция не
является НИ
ЧЕТНОЙ, НИ
НЕЧЕТНОЙ
(общего вида)

28.

ИНСТРУКЦИЯ К РЕШЕНИЮ
Для того чтобы выяснить четная или нечетная функция
необходимо:
- найти область определения функции D(f) (значения для x)
и показать, что эта область
симметрична относительно 0.
-найти f(-x) и если: f(-x)= f(x), то функция четная, а если
f(-x)=-f(x), то функция нечетная.

29.

10
График четной
функции
симметричен
относительно
оси ординат:
9
8
7
6
5
4
3
2
1
0
-4
-3
-2
-1
0
1
2
3
4
При построении графиков четных функций используется
осевая симметрия относительно оси ординат.

30.

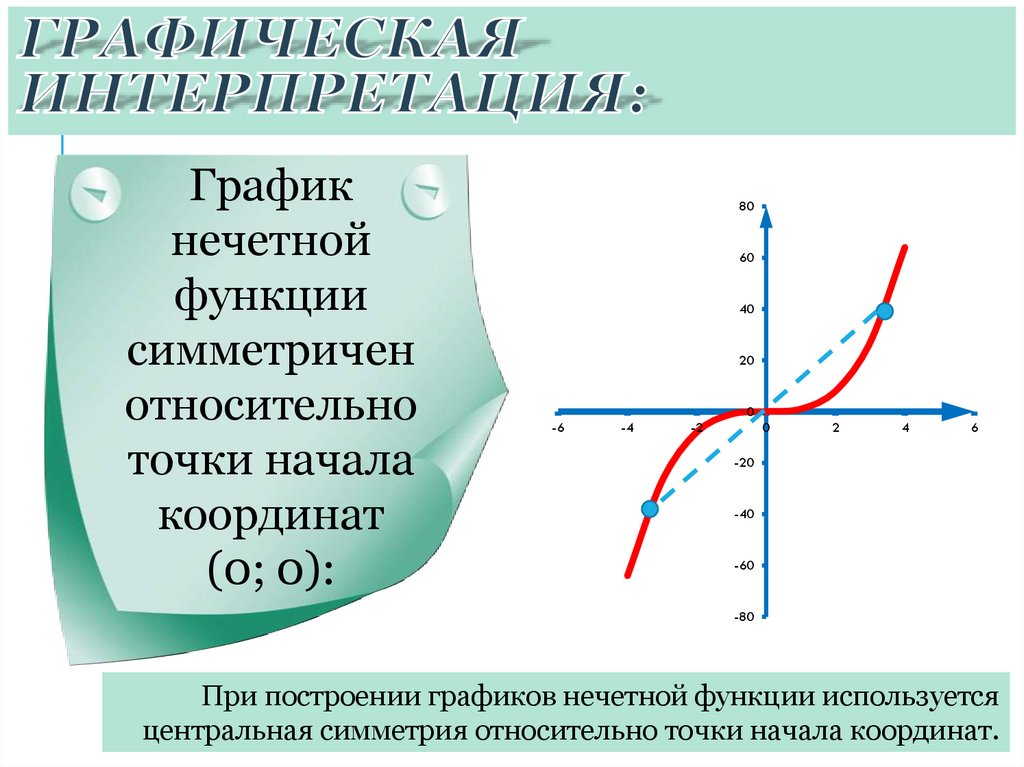
График
нечетной
функции
симметричен
относительно
точки начала
координат
(0; 0):
80
60
40
20
0
-6
-4
-2
0
2
4
6
-20
-40
-60
-80
При построении графиков нечетной функции используется
центральная симметрия относительно точки начала координат.

31.

Является ли множество [−10;10) симметричным?
a.
нет
b.
да

32.

Выберите чётную функцию
1.
f(x)=x2-2/x4
2.
y=-x5
3.
g(x)=21+9x
Областью определения данной функции является
a.
D(y)=(−∞;0)∪(0;+∞)
b.
D(y)=(−1;5)
c.
D(y)=(−∞;+∞)

33.

Определите, чётная ли данная функция f(x)=-x2
a.
Данная функция нечётная
b.
данная функция чётная
c.
Данная функция ни чётная, ни нечётная

34.

Даны функции:
1. y=-x/7
2. y=x7-2x
3. y=9x+10
4. y=2x5−7x+10
Из них нечётными являются функции
a.
1; 3; 4.
b.
все
c.
1; 2.
d.
ни одна
e.
4.
f.
y=-x/7

35.

На рисунке изображён
a.
График нечётной функции
b.
График чётной функции
c.
График функции общего вида

36.

Представьте функцию f(x) = 2x6+11x9+12x4+7x в виде суммы
чётной и нечётной функций.
Ответ:
x
+
x
+
x
+

37.

На координатной плоскости нарисуйте ломаную, ABC с координатами
A(0;0);B(−2;−3);C(−4;2).
Продолжите рисовать ломаную так, чтобы получился график чётной
функции. Запишите координаты, которые необходимы для построения
графика чётной функции.
А1 =
В1 =
С1 =
;
;
;

38.

На координатной плоскости нарисуйте ломаную ABC с координатами
A(0;0),B(−4;4),C(−6;-2).
Продолжите рисовать ломаную так, чтобы получился график нечётной
функции. Запишите координаты, которые необходимы для построения
графика нечётной функции.
А1 =
В1 =
С1 =
;
;
;

39.

40.

41.

Чаще всего функция выражается суммой, произведением или
отношением двух и более чётных или нечётных функций или
представляет собой сочетание нескольких чётных и нечётных
функций. Как быстро доказать чётная функция или нечётная?
Чтобы ответить на эти вопросы проведите дома исследование
различных функций и сформулируйте правила, которые
позволят нам сразу определять чётная функция или нечётная.
—сумма двух чётных функций –
—сумма двух нечётных функций –
—произведение двух нечётных функций —произведение двух чётных функций –
—отношение двух чётных функций —отношение двух нечётных функций —сумма нечётной и чётной функций —произведение нечётной и чётной функций —отношение нечётной и чётной функций -