Четность, нечетность, периодичность тригонометрических функций

1. Четность, нечетность, периодичность тригонометрических функций

2.

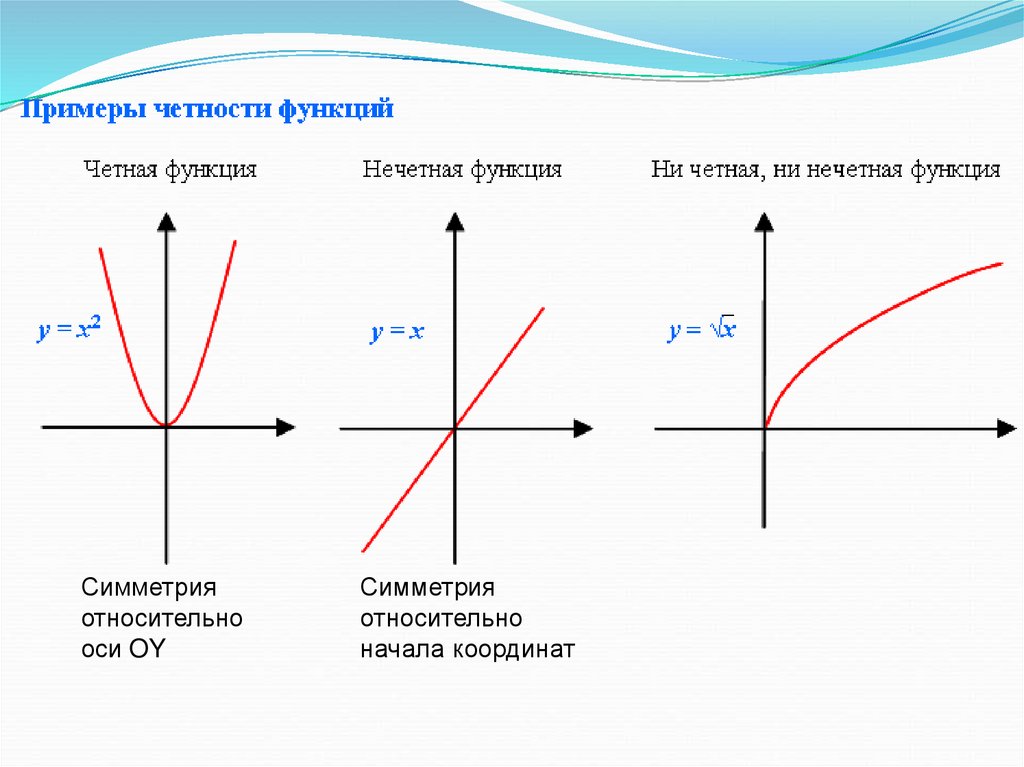
Четная и нечетная функция
Функцию y = f(x), x ∈ X, называют чётной, если для
любого значения x из множества X выполняется
равенство f(−x) = f(x).
Функцию y = f(x), x ∈ X, называют нечётной, если для
любого значения x из множества X выполняется
равенство f(−x) = −f(x)
Периодическая функция
Функция называется периодической, если для всех х
из области определения функции выполняется
равенство f ( x) f ( x Т ) f ( x T )
Т- некоторое число, называемое периодом функции.

3.

Симметрия
относительно
оси OY
Симметрия
относительно
начала координат

4. Функции y = sin x, y = tg x, y = ctg x — нечетные, y = cos x — четная. sin (- x) = - sin x cos (- x) = cos x tg (- x) = - tg x

5.

Решить в классной работе № 700(1,3,5), 701(1)

6.

Решить в классной работе № 702(1,3,5), 703(1,3)
Наименьший положительный период функции
y=sinx
y=cosx
T=2π
y=tgx
y=ctgx
T=π

7.

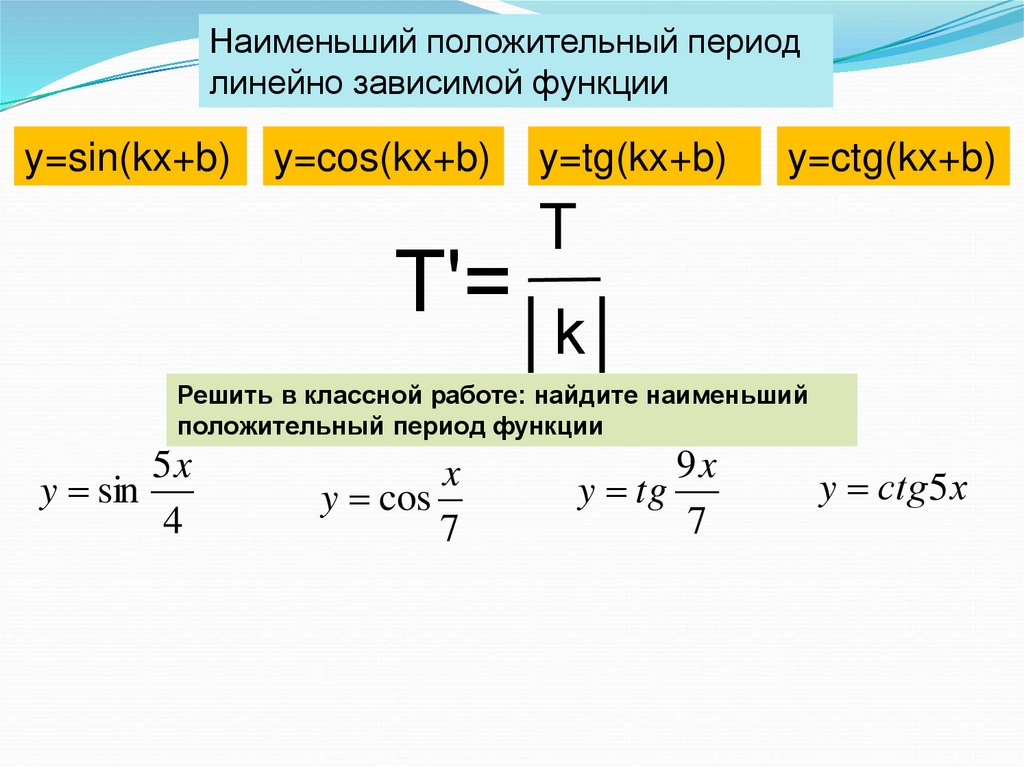
Наименьший положительный период
линейно зависимой функции
y=sin(kx+b)
y=cos(kx+b)
y=tg(kx+b)
y=ctg(kx+b)
T
Tʹ=│k│
Решить в классной работе: найдите наименьший
положительный период функции
5x
y sin
4
x
y cos
7
9x
y tg
7
y сtg 5 х

8. Домашнее задание

Выучить § 39, конспект, решить № 700(2,4,6),
701(2), 703(2,4), 705