Similar presentations:
Тригонометрические функции
1.
2.
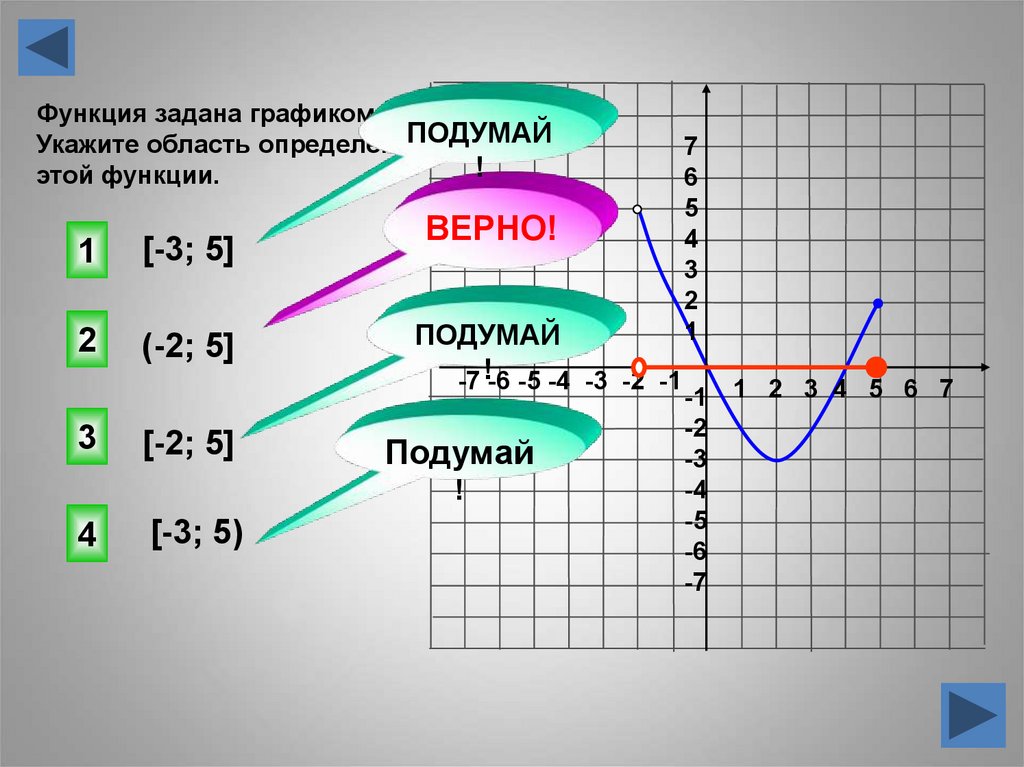
Функция задана графиком.ПОДУМАЙ
Укажите область определения
!
этой функции.
1
[-3; 5]
2
(-2; 5]
3
[-2; 5]
ВЕРНО!
ПОДУМАЙ
-7 !-6 -5 -4 -3 -2 -1
Подумай
!
4
[-3; 5)
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
1 2 3 4 5 6 7
3.
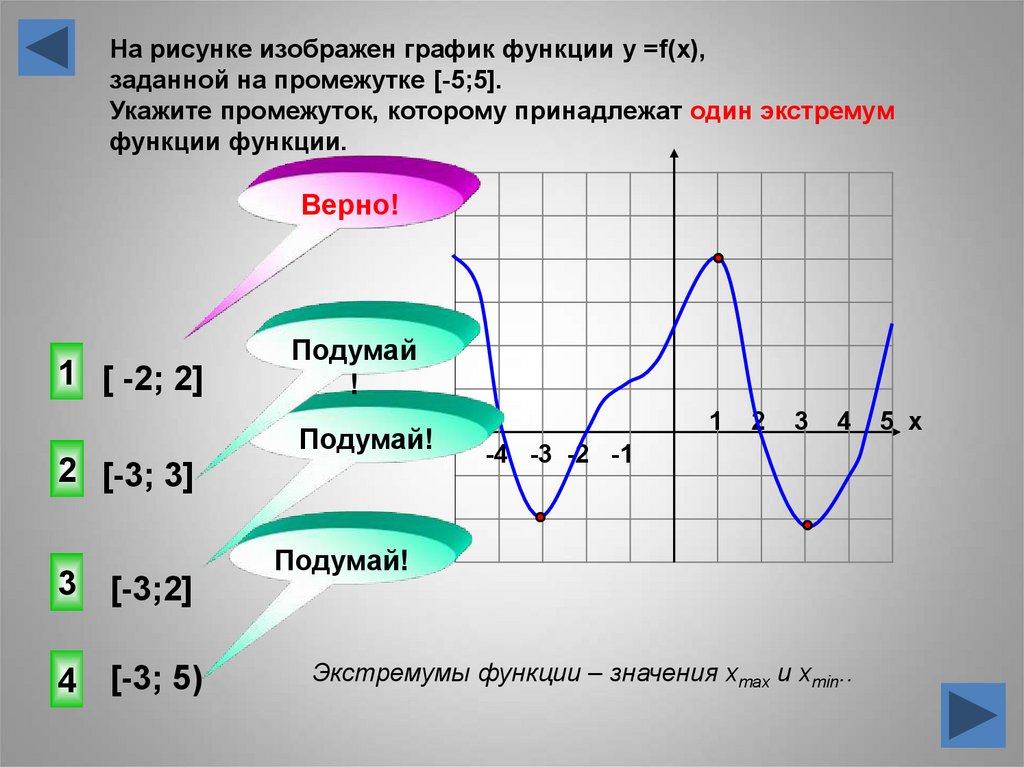
На рисунке изображен график функции у =f(x),заданной на промежутке [-5;5].
Укажите промежуток, которому принадлежат один экстремум
функции функции.
Верно!
1 [ -2; 2]
Подумай
!
Подумай!
2 [-3; 3]
3 [-3;2]
4 [-3; 5)
1
2
3
4
-4 -3 -2 -1
Подумай!
Экстремумы функции – значения xmax и xmin..
5 х
4.
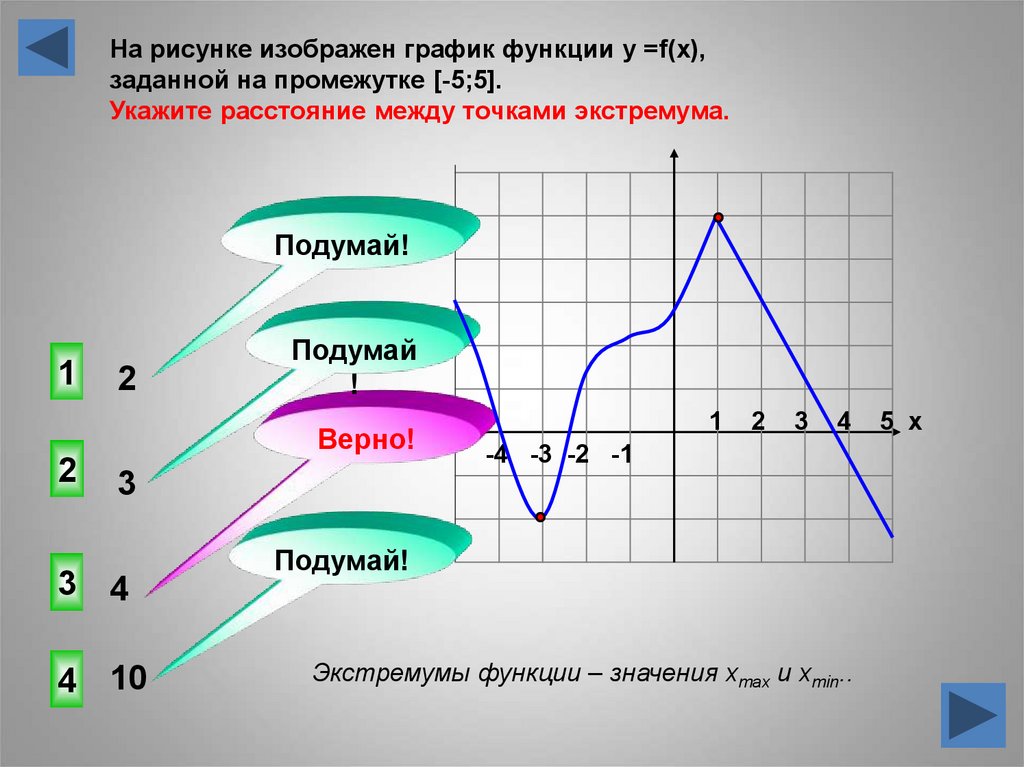
На рисунке изображен график функции у =f(x),заданной на промежутке [-5;5].
Укажите расстояние между точками экстремума.
Подумай!
1
2
Подумай
!
Верно!
2
1
2
3
4
-4 -3 -2 -1
3
3 4
4 10
Подумай!
Экстремумы функции – значения xmax и xmin..
5 х
5.
Указать наименьшее инаибольшее значение
выражения
1 cos
1; 1
0; 2
2; 0
1; 3
6.
В древности тригонометрия возникла в связи с потребностямиастрономии, землемерия и строительного дела, то есть носила
чисто геометрический характер и представляла главным
образом «исчисление хорд». Со временем в нее начали
вкрапляться некоторые аналитические моменты. В первой
половине 18-го века произошел резкий перелом, после чего
тригонометрия приняла новое направление и сместилась в
сторону математического анализа. Именно в это время
тригонометрические зависимости стали рассматриваться как
функции.
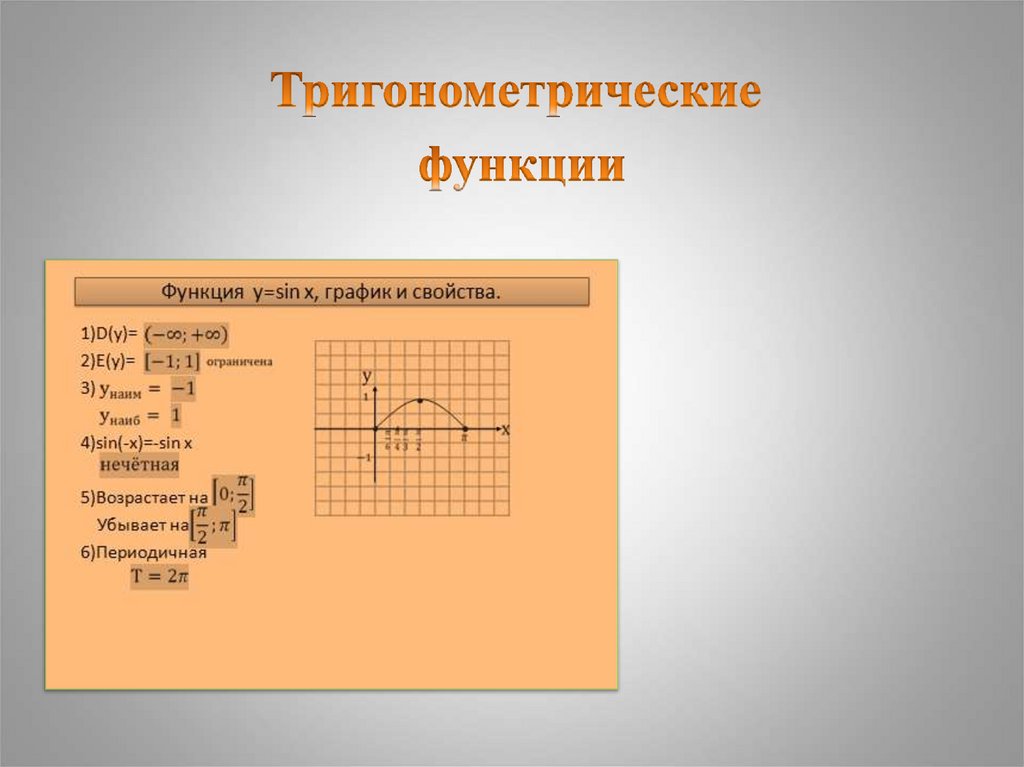
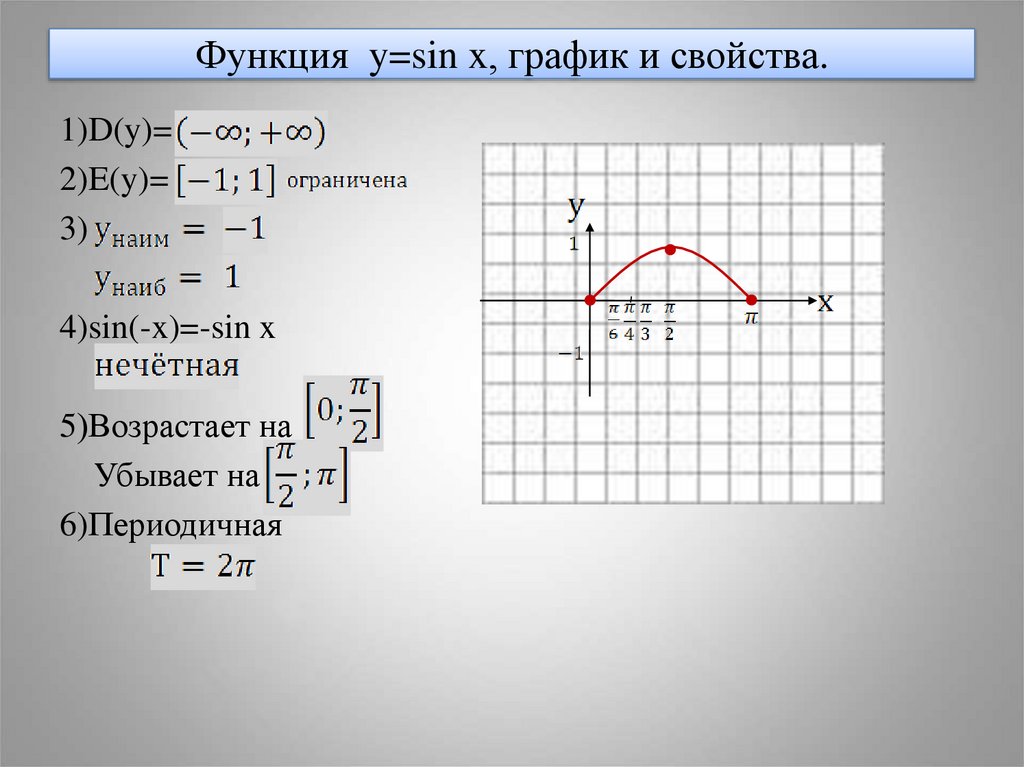
7. Функция y=sin x, график и свойства.
1)D(y)=2)E(y)=
3)
4)sin(-x)=-sin x
5)Возрастает на
Убывает на
6)Периодичная
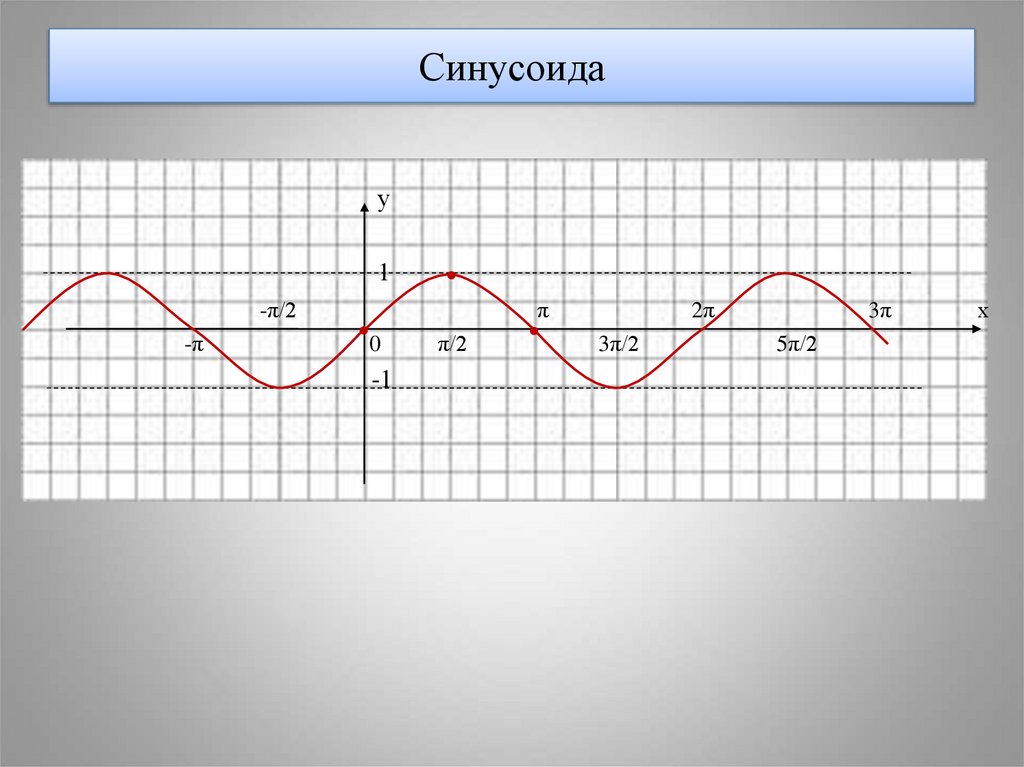
8. Синусоида
у1
π
-π/2
-π
0
-1
π/2
2π
3π/2
3π
5π/2
х
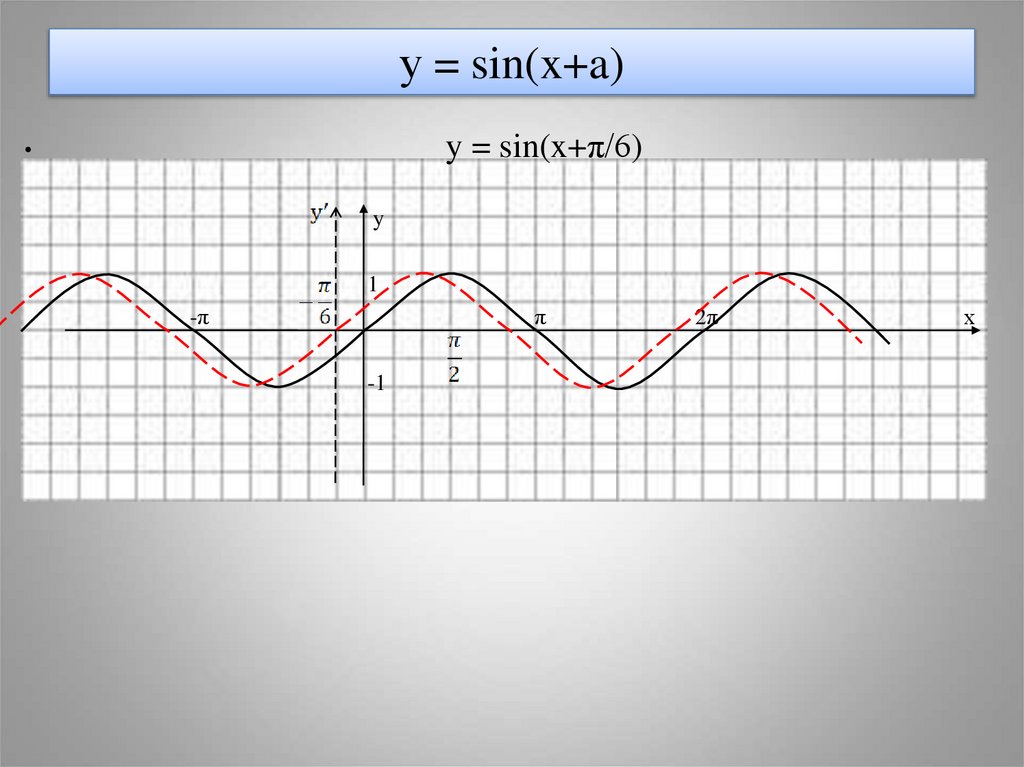
9. у = sin(x+a)
y = sin(x+π/6)y
1
π
-π
-1
2π
х
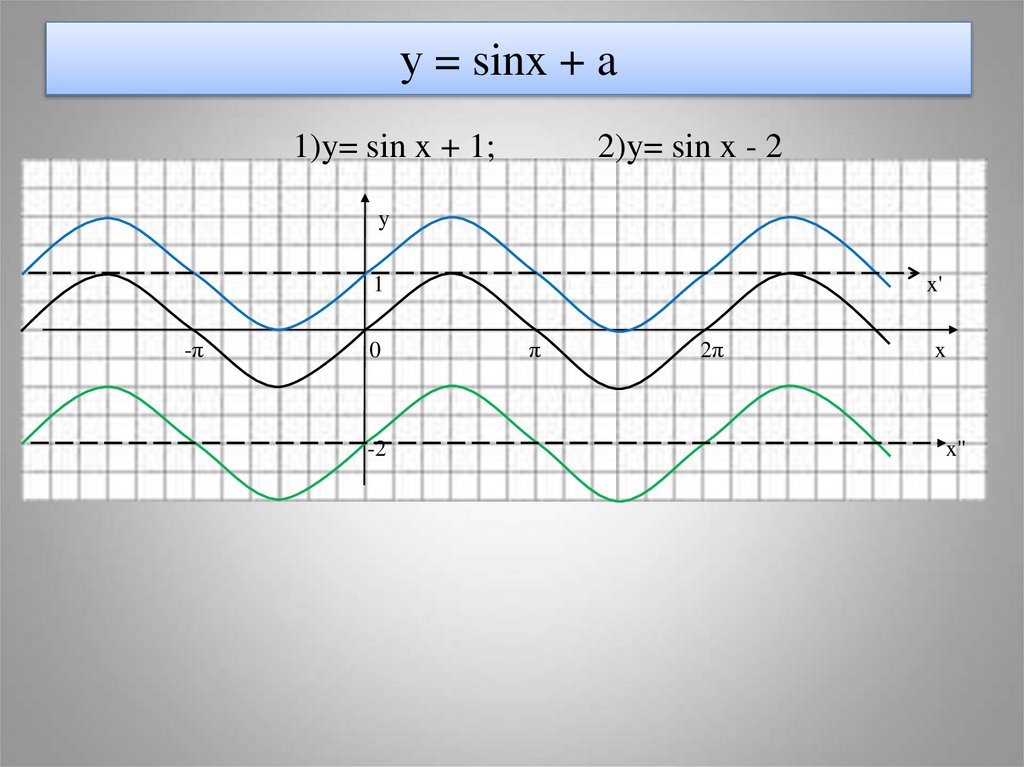
10. у = sinx + a
1)y= sin x + 1;2)y= sin x - 2
y
1
-π
0
-2
x'
π
2π
x
x''
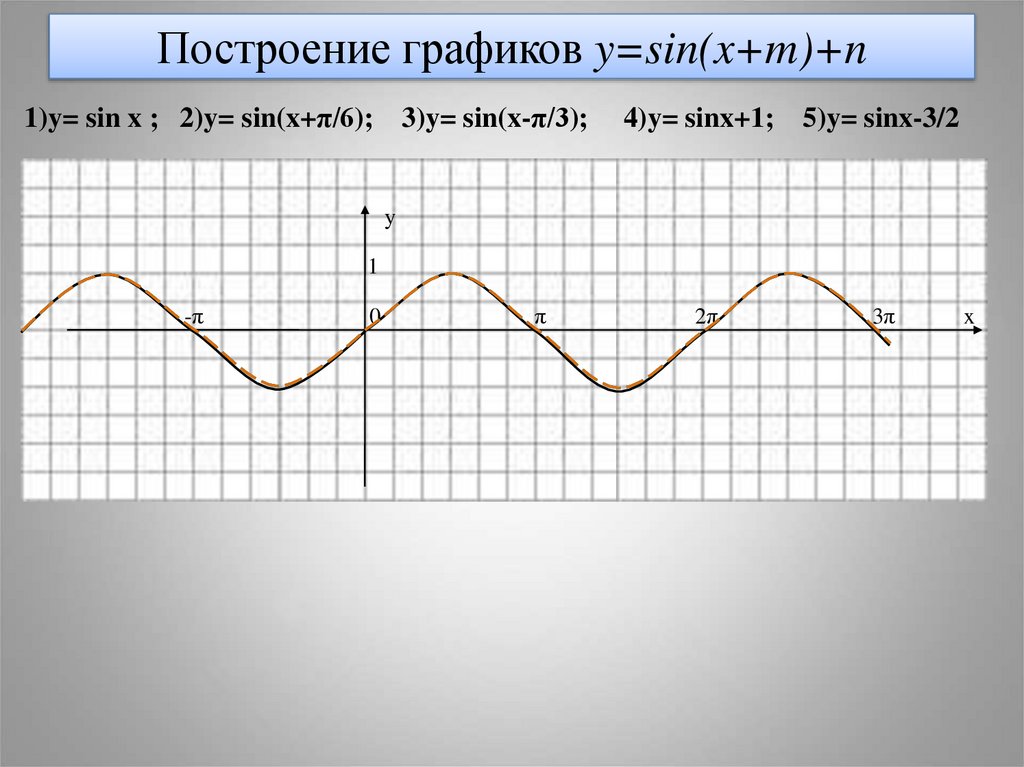
11. Построение графиков y=sin(x+m)+n
1)y= sin x ; 2)y= sin(x+π/6); 3)y= sin(x-π/3);4)y= sinx+1; 5)y= sinx-3/2
y
1
-π
0
π
2π
3π
x
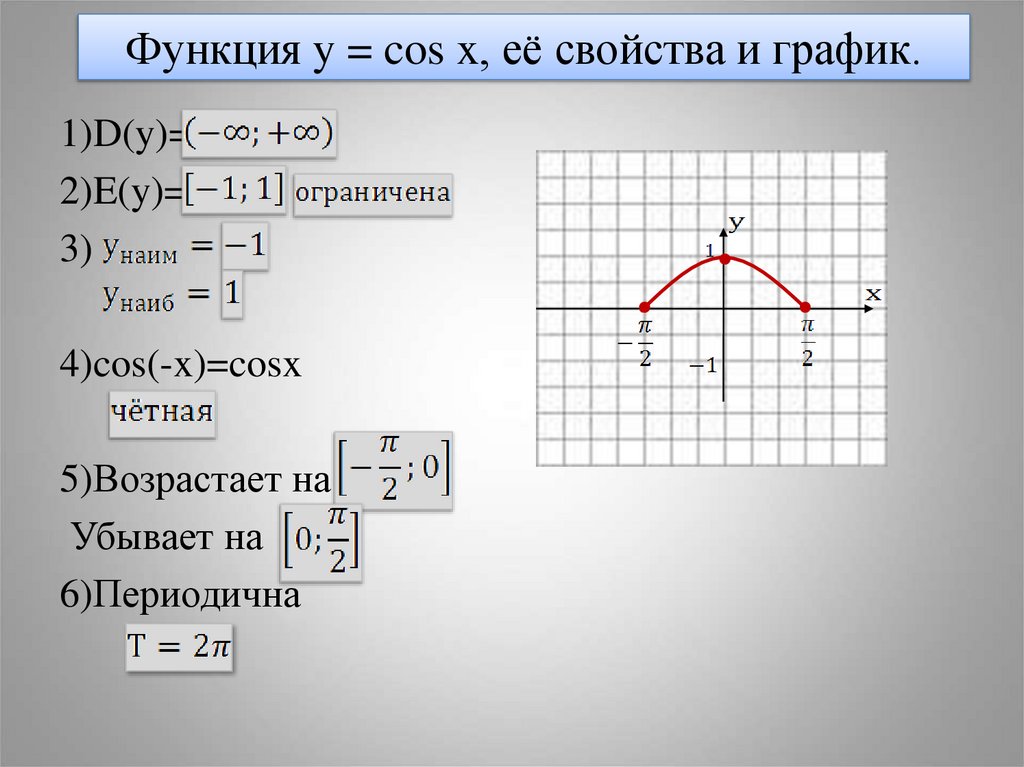
12. Функция y = cos x, её свойства и график.
1)D(y)=2)E(y)=
3)
4)cos(-x)=cosx
5)Возрастает на
Убывает на
6)Периодична
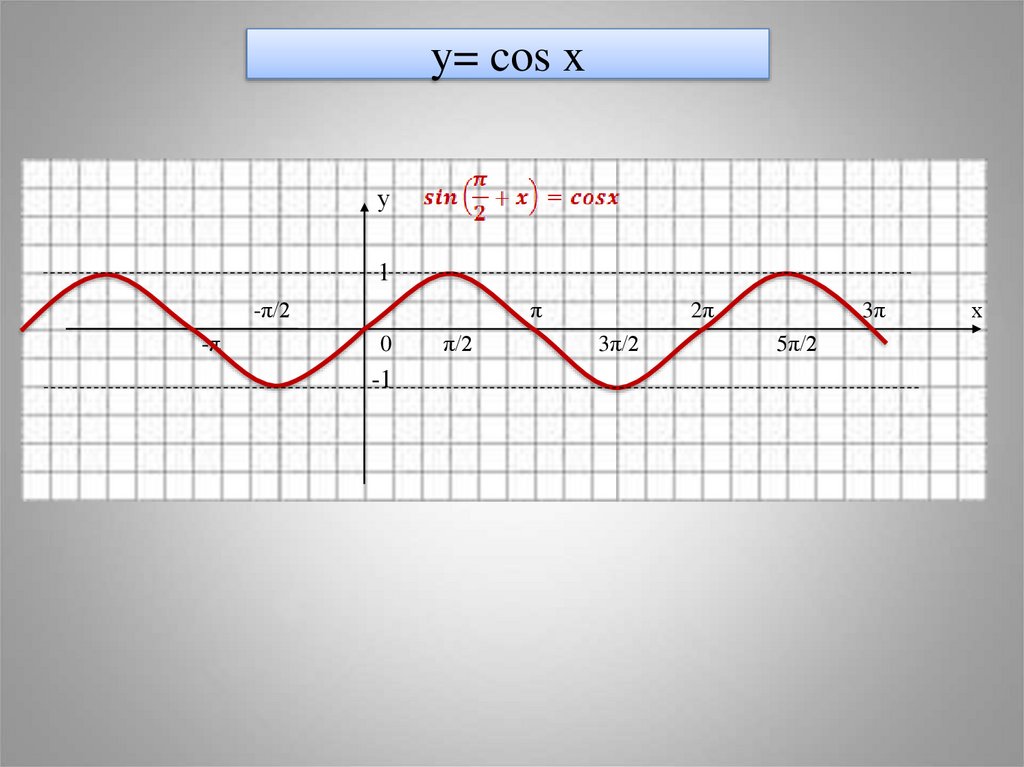
13. y= cos x
у1
π
-π/2
-π
0
-1
π/2
2π
3π/2
3π
5π/2
х
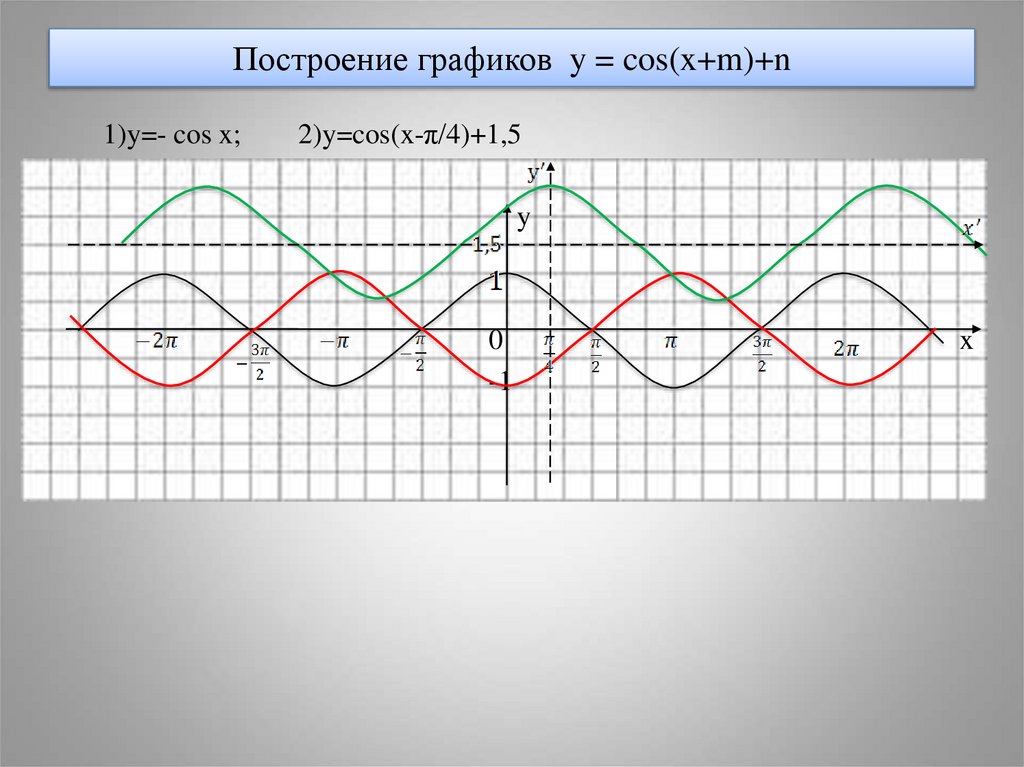
14. Построение графиков y = cos(x+m)+n
1)y=- cos x;2)y=cos(x-π/4)+1,5
y
0
-1
x
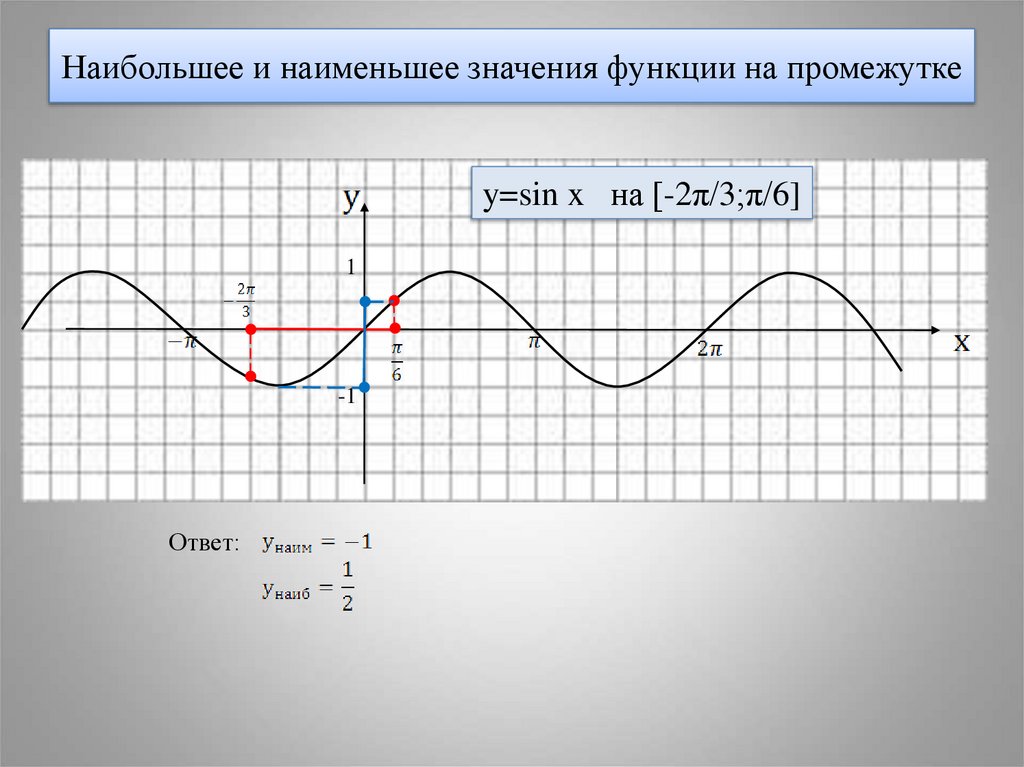
15. Наибольшее и наименьшее значения функции на промежутке
y=sin x на [-2π/3;π/6]1
-1
Ответ:
16.
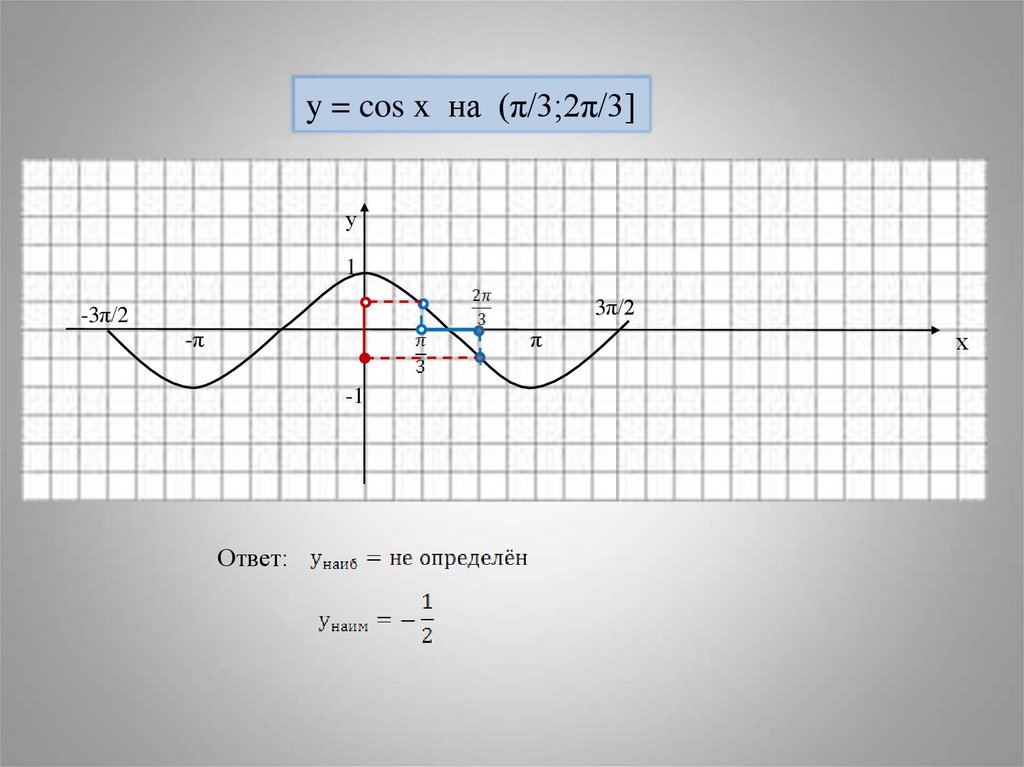
y = cos x на (π/3;2π/3]у
1
3π/2
-3π/2
π
-π
-1
Ответ:
х
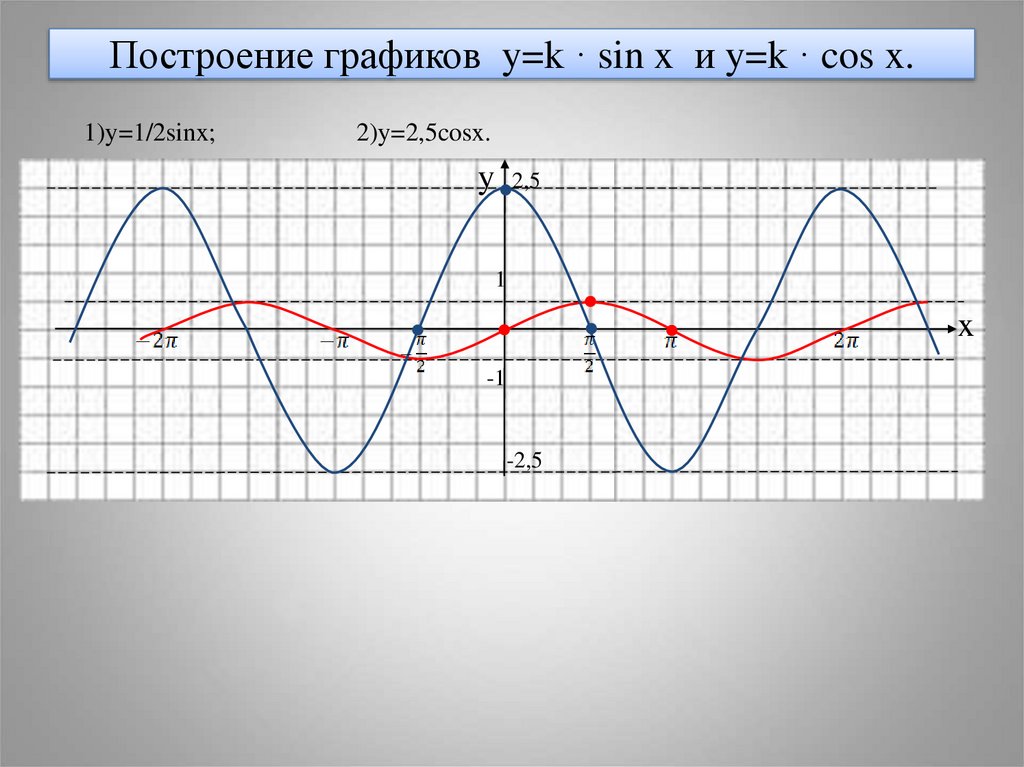
17. Построение графиков y=k · sin x и y=k · cos x.
1)y=1/2sinx;2)y=2,5cosx.
y 2,5
1
x
-1
-2,5
18. Множество значений функции
Пример: y=-9cos(x+π/6)-0,5-1≤ cosx ≤1
-1≤ cos(x+π/6) ≤1
-9≤ -9cos(x+π/6) ≤9
-9,5≤ -9cos(x+π/6)-0,5 ≤8,5 yЄ[-9,5;8,5]
1)y=sinx-3;
2)y= cos(x+π/3);
3)y=sin(-2x+π)+1;
4)y=5cosx;
5)y= -sinx;
7)y=-4sin(x+1)+7; 8)y=
cosx- ;
6)y=1/2cosx-3;
9)y=-1-sin .
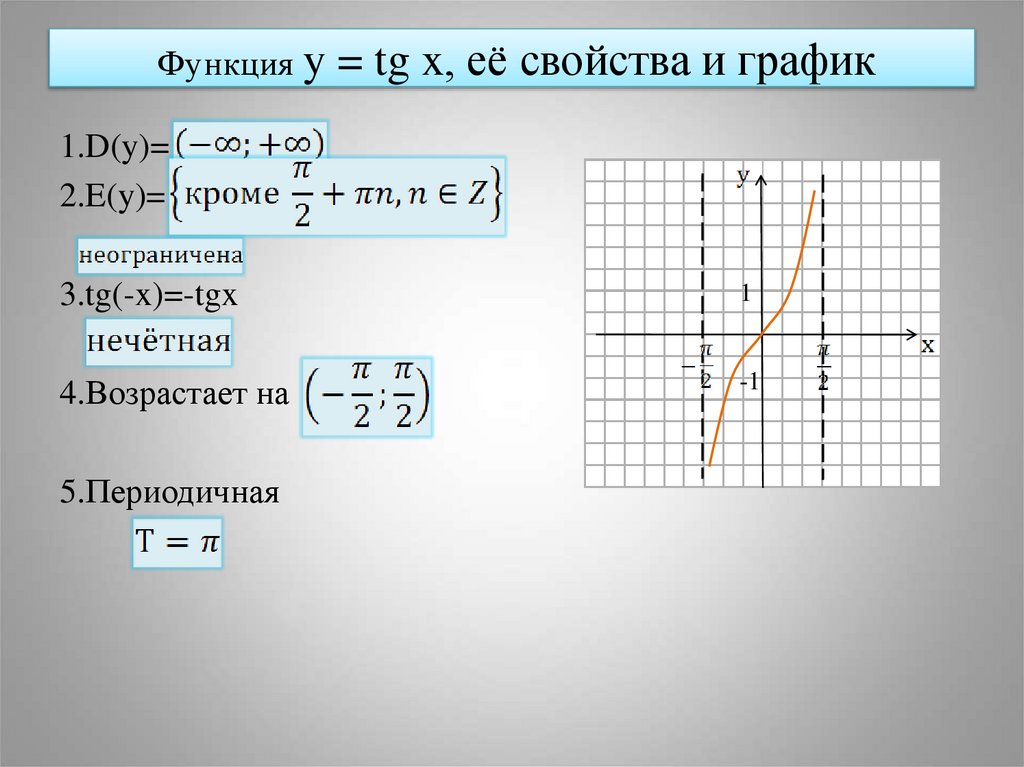
19. Функция y = tg x, её свойства и график
1.D(y)=2.E(y)=
3.tg(-x)=-tgx
1
4.Возрастает на
-1
5.Периодичная
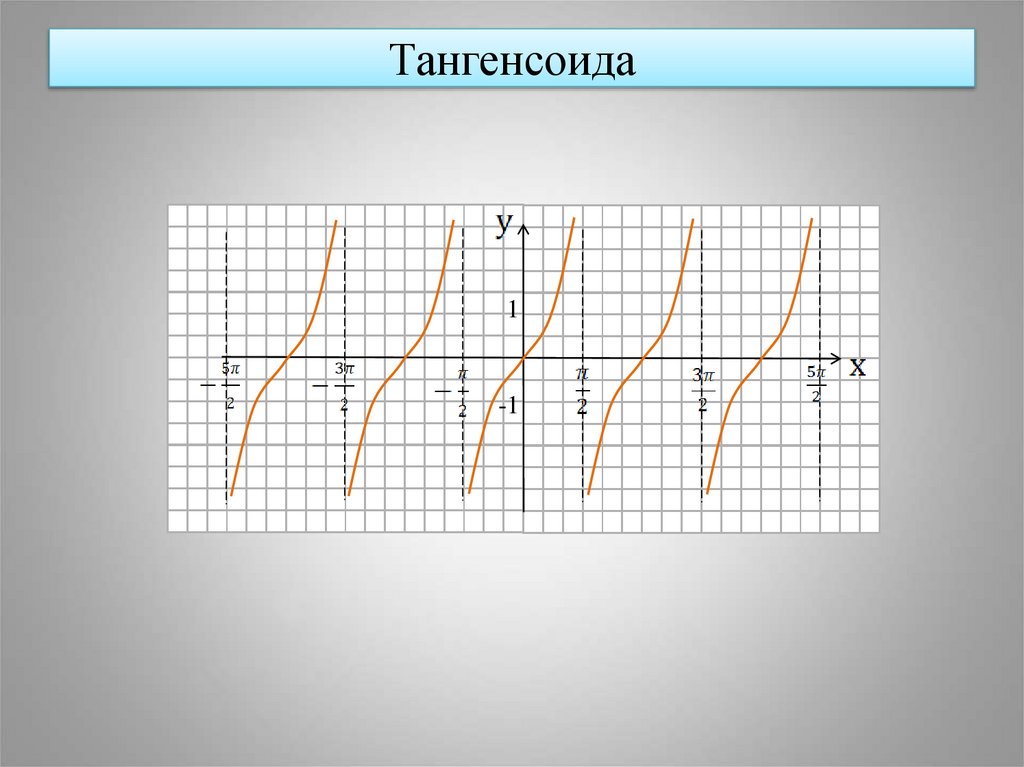
20. Тангенсоида
1-1
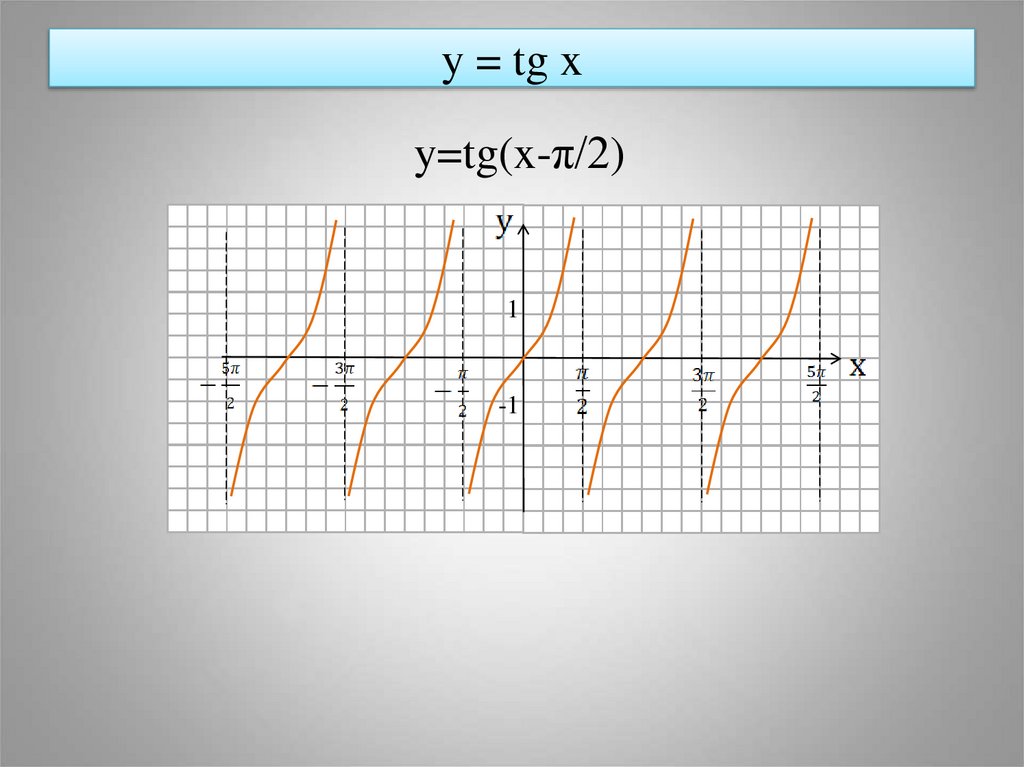
21. y = tg x
y=tg(x-π/2)1
-1
22. Периодичность
1)x; x+T; x-TЄD(f)2) Если y=f(x) периодичная с периодом Т₁‡0, то
y=A· f(kx+m)+B периодичная с периодом
Примеры:
1) y=sin4x Т₁=2π
2) y=-4cos(x/3-1)+2
T₁=2π
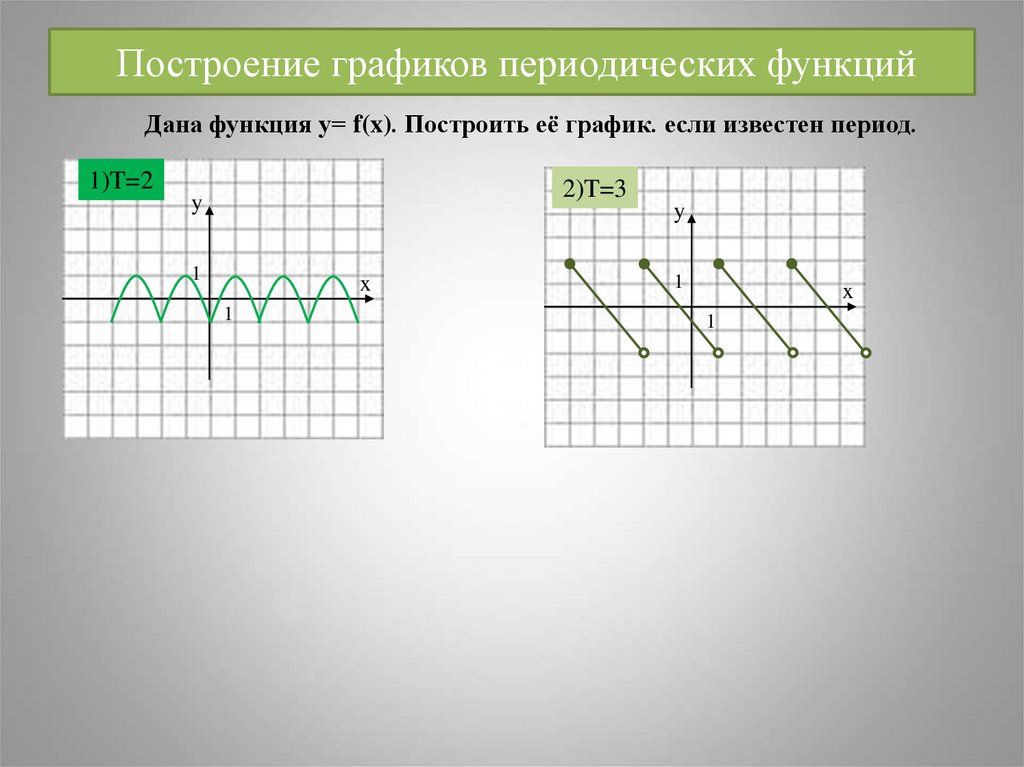
23. Построение графиков периодических функций
Дана функция у= f(x). Построить её график. если известен период.1)T=2
2)T=3
y
y
1
x
1
1
x
1
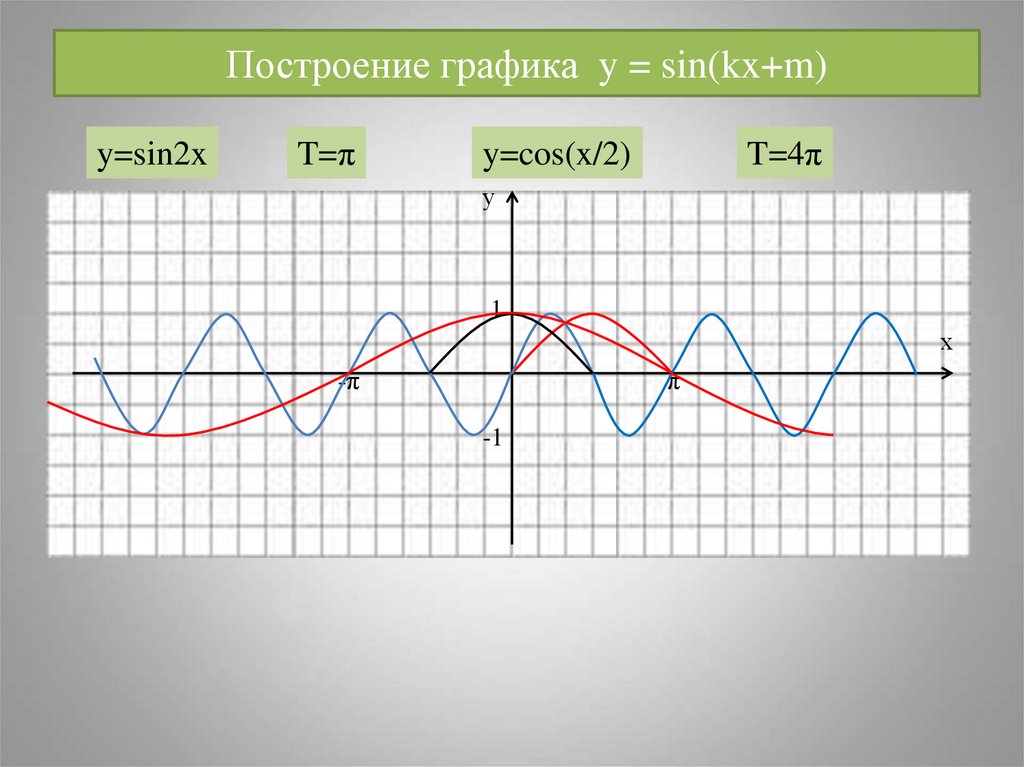
24. Построение графика y = sin(kx+m)
y=sin2xT=π
y=cos(x/2)
T=4π
у
1
х
π
-π
-1
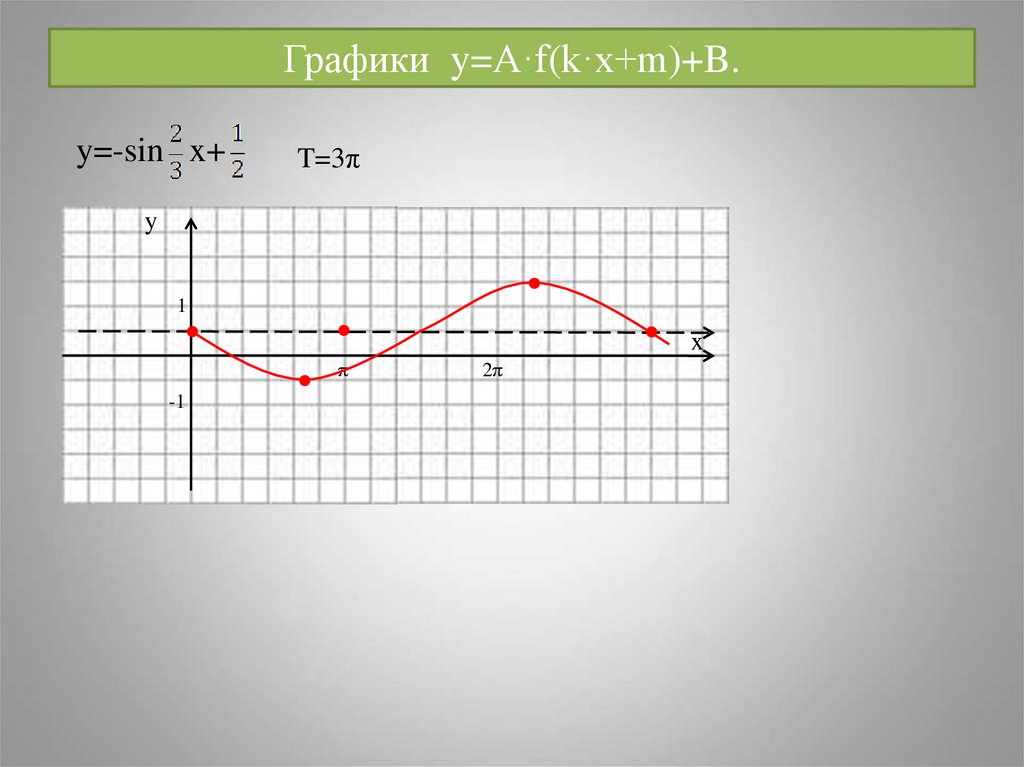
25. Графики y=A·f(k·x+m)+B.
y=-sin x+T=3π
y
1
x
π
-1
2π
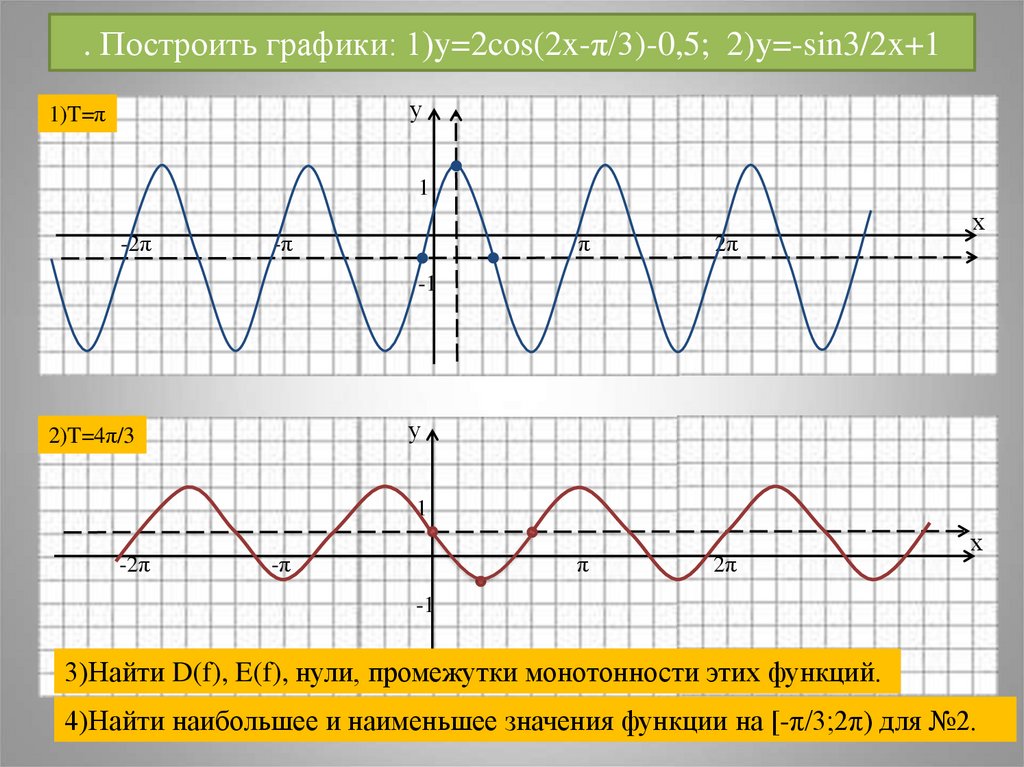
26. . Построить графики: 1)y=2cos(2x-π/3)-0,5; 2)y=-sin3/2x+1
у1)T=π
1
-2π
π
-π
х
2π
-1
у
2)T=4π/3
1
-2π
π
-π
х
2π
-1
3)Найти D(f), E(f), нули, промежутки монотонности этих функций.
4)Найти наибольшее и наименьшее значения функции на [-π/3;2π) для №2.




 mathematics
mathematics








