Вычисление объемов пространственных тел с помощью интеграла

1.

Вычисление объемов
пространственных тел
с помощью интеграла.
Воробьев Леонид Альбертович, г.Минск

2.

Немного теории.
Чтобы получить представление об общем методе вычисления объемов различных
пространственных фигур, попробуем найти объем лимона. Ни на одно из тел,
изучаемых в школе (призма, пирамида, шар, конус и т.д.), лимон не похож. Однако,
мы можем поступить как все хозяйки – разрезать лимон на тонкие ломтики, размер
которых зависит от расстояния x, причем x [0;H].
x
H
Тогда, по свойству объема, сумма объемов всех ломтиков даст нам объем всего
лимона.

3.

Немного теории.
С точки зрения геометрии мы построили сечения пространственной фигуры
плоскостями, перпендикулярными оси фигуры; причем, если принять число
разбиений бесконечно большим числом (n→ ), то:
x
H
x
H
x
0
n
Проще говоря, при бесконечном числе
разбиений каждый ломтик «вырождается» в
плоское сечение и объем лимона равен
бесконечной интегральной сумме площадей
таких сечений, зависящих от расстояния x, т.е.
H
Vëčě î í ŕ
S
ńĺ ÷.
dx,
0
где H – высота тела, а Sсеч. – некоторая
функция, зависящая от x, причем x [0;H].

4.

Немного теории (базовые классы могут пропустить).
Если принять число разбиений бесконечно большим числом (n→ ), то:
H
x
n
x
H
lim x lim
0
n Ґ
n Ґ n
x
Vëčě î í ŕ lim V1 V2 ... Vn
n Ґ
lim x·S1 x·S 2 ... x·S n
x 0
H
H
lim x S1 S 2 ... S n S ńĺ ÷.dx
x 0
0
H
Vëčě î í ŕ
S
ńĺ ÷.
dx,
0
где H – высота тела, а Sсеч. – некоторая
функция, зависящая от x, причем x [0;H].

5.

I. Объем прямоугольного параллелепипеда
с высотой H и площадью основания S.
x [0;H]
x
Площадь сечения не изменяется в любой
точке отрезка от 0 до H и равна площади
основания.
H
x
0
H
H
0
0
V Sńĺ ÷.dx Sî ńí . dx Sî ńí . ·x
H
0
Sî ńí . ·H ęóá.ĺ ä.

6.

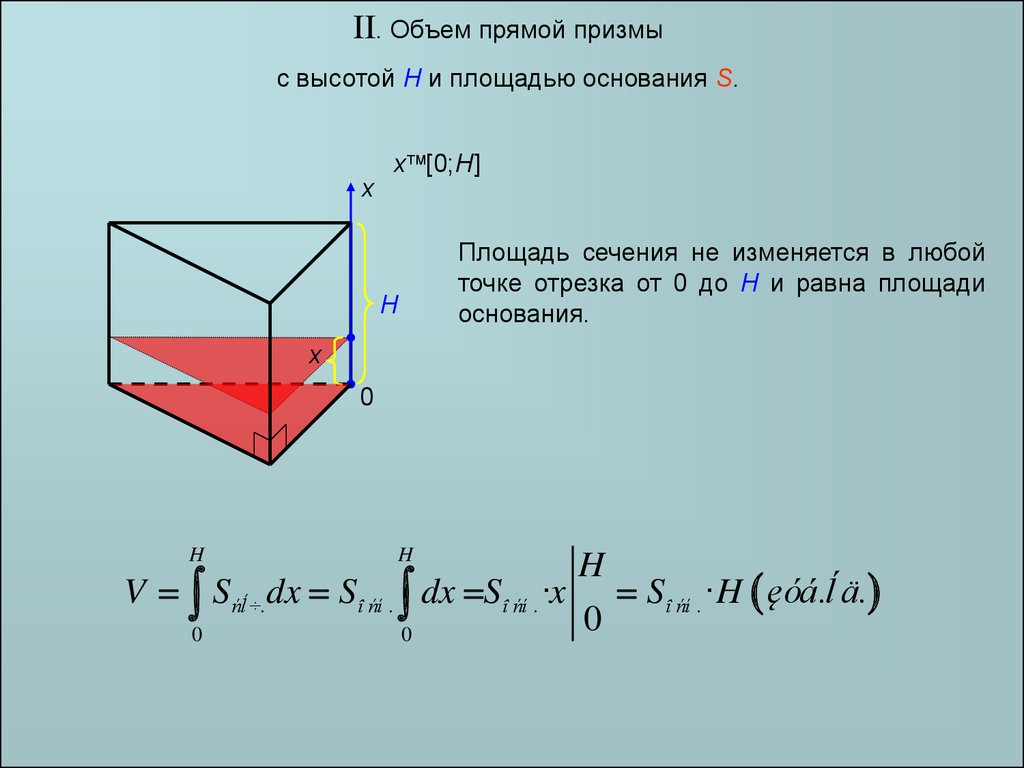
II. Объем прямой призмы
с высотой H и площадью основания S.
x [0;H]
x
Площадь сечения не изменяется в любой
точке отрезка от 0 до H и равна площади
основания.
H
x
0
H
H
0
0
V Sńĺ ÷.dx Sî ńí . dx Sî ńí . ·x
H
0
Sî ńí . ·H ęóá.ĺ ä.

7.

III. Объем n-угольной прямой призмы
с высотой H и площадью основания S.
x [0;H]
Площадь сечения не изменяется в любой
точке отрезка от 0 до H и равна площади
основания.
x
H
x
0
H
H
0
0
V Sńĺ ÷.dx Sî ńí . dx Sî ńí . ·x
H
0
Sî ńí . ·H ęóá.ĺ ä.

8.

IV. Объем наклонной призмы
с высотой H и площадью основания S.
x [0;H]
x
Площадь
сечения,
перпендикулярного
высоте, не изменяется в любой точке
отрезка от 0 до H и равна площади
основания.
H
x
0
H
H
0
0
V Sńĺ ÷.dx Sî ńí . dx Sî ńí . ·x
H
0
Sî ńí . ·H ęóá.ĺ ä.

9.

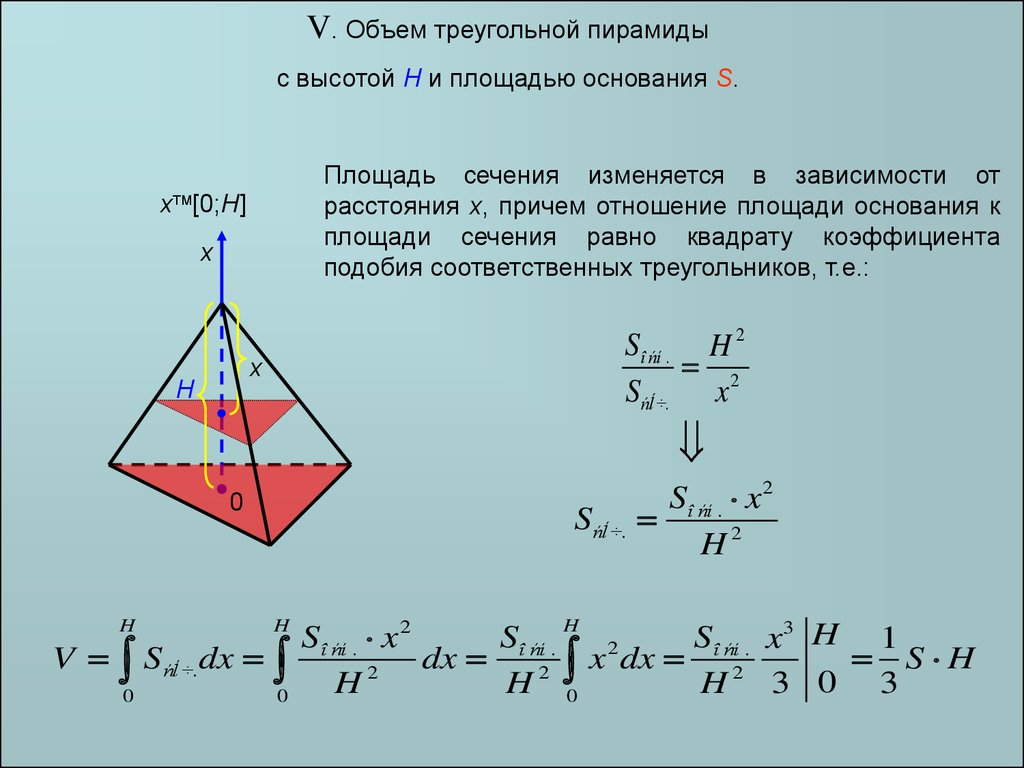
V. Объем треугольной пирамиды
с высотой H и площадью основания S.
Площадь сечения изменяется в зависимости от
расстояния x, причем отношение площади основания к
площади сечения равно квадрату коэффициента
подобия соответственных треугольников, т.е.:
x [0;H]
x
Sî ńí . H 2
2
Sńĺ ÷. x
x
H
0
H
V
S
0
Sńĺ ÷.
H
dx
ńĺ ÷.
0
Sî ńí . x 2
H2
H
Sî ńí . x 2
Sî ńí .
Sî ńí . x 3 H 1
2
dx
x dx
S H
2
2
2
H
H 0
H 3 0 3

10.

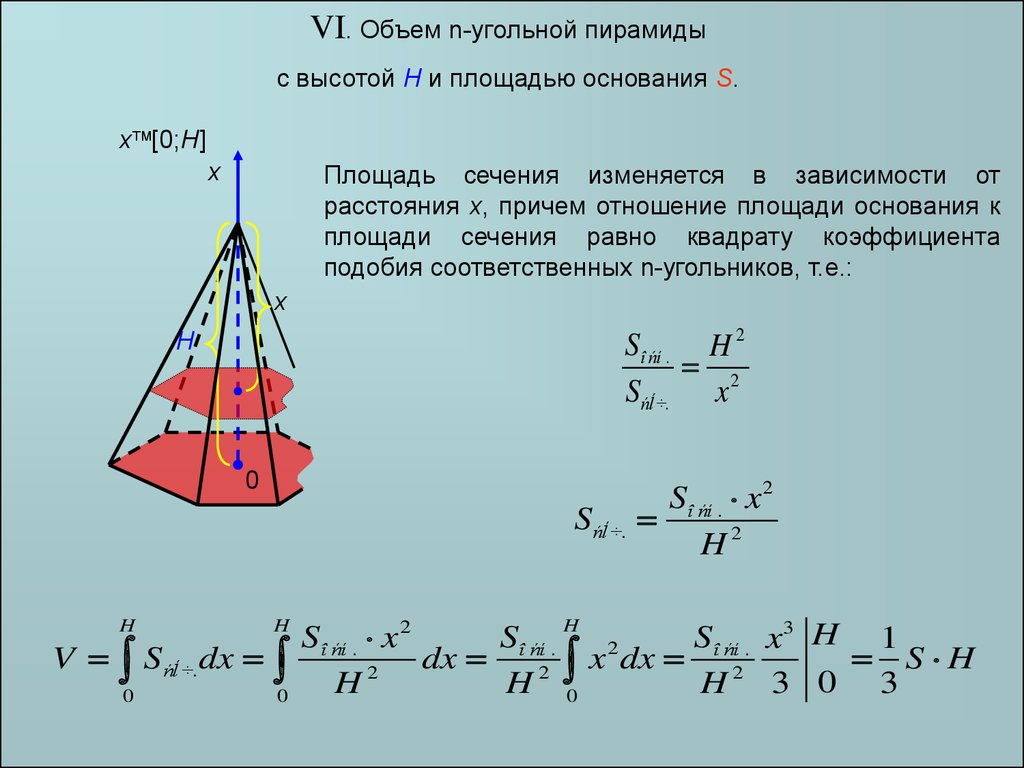
VI. Объем n-угольной пирамиды
с высотой H и площадью основания S.
x [0;H]
Площадь сечения изменяется в зависимости от
расстояния x, причем отношение площади основания к
площади сечения равно квадрату коэффициента
подобия соответственных n-угольников, т.е.:
x
x
Sî ńí . H 2
2
Sńĺ ÷. x
H
0
Sńĺ ÷.
H
V
S
0
H
dx
ńĺ ÷.
0
Sî ńí . x 2
H2
H
Sî ńí . x 2
Sî ńí .
Sî ńí . x 3 H 1
2
dx
x dx
S H
2
2
2
H
H 0
H 3 0 3

11.

VII. Объем усеченной пирамиды.
текст

12.

VIII. Объем цилиндра с высотой H и площадью основания S.
x [0;H]
x
Площадь сечения не изменяется в любой
точке отрезка от 0 до H и равна площади
основания.
H
x
0
H
H
0
0
V Sńĺ ÷.dx Sî ńí . dx Sî ńí . ·x
H
0
Sî ńí . ·H R 2 H ęóá.ĺ ä.

13.

IX. Объем конуса с высотой H и площадью основания S.
x [0;H]
Площадь сечения изменяется в зависимости от
расстояния x, причем отношение площади основания к
площади сечения равно квадрату коэффициента
подобия соответственных кругов, т.е.:
x
x
Sî ńí . H 2
2
Sńĺ ÷. x
H
0
Sńĺ ÷.
H
V
S
0
H
dx
ńĺ ÷.
0
Sî ńí . x 2
H2
H
Sî ńí . x 2
Sî ńí .
Sî ńí . x 3 H 1
2
dx
x dx
S H
2
2
2
H
H 0
H 3 0 3

14.

X. Объем усеченного конуса.
текст

15.

XI. Объем шара с радиусом R.
Найдем
объем
полушария,
как
бесконечную
интегральную сумму площадей сечения с радиусом r, где:
r R 2 x 2 , x 0; R
x
R
Vďî ëóř ŕ đč˙
R
x
R
2
2
S
dx
r
dx
R
x
dx
ńĺ ÷.
2
0
r
R
0
0
2
3 R 3 2 R 3
x3 R
R x
ęóá.ĺ ä.
R
3 0
3
3
0
Значит, объем всего шара равен:
Vř ŕ đŕ
2 R3 4 R3
2·
ęóá.ĺ ä.
3
3

16.

XII. Объем шарового сегмента.
Вывод объема шарового сегмента с высотой h и
радиусом основания r отличается от вывода объема
полушария нижним пределом интегрирования. В данном
случае он равен R –h :
R
Vńĺ ăě ĺ í ň ŕ
hh
R h
x
R
Sńĺ ÷.dx
R
R h
r dx
2
ńĺ ÷.
R
R
2
x 2 dx
R h
3
3
h
R
2
R
x3 R
2
3
R R h
R
R x
3
3
3 R h
2 h3
2 R3
R 3 3R 2 h 3Rh 2 h3
2
3
R R h
Rh
3
3
3
h
h 2 R ęóá.ĺ ä.
3
Обратите внимание, что в формуле объема шарового сегмента участвует радиус
шара (R), а не радиус основания сегмента (r)!

17.

XIII. Объем шарового слоя.
текст

18.

XIV. Объем шарового сектора.
текст
h
R