Similar presentations:
Вычисление объемов тел вращения
1. Вычисление объемов тел вращения
Применение интеграла11 класс
2.
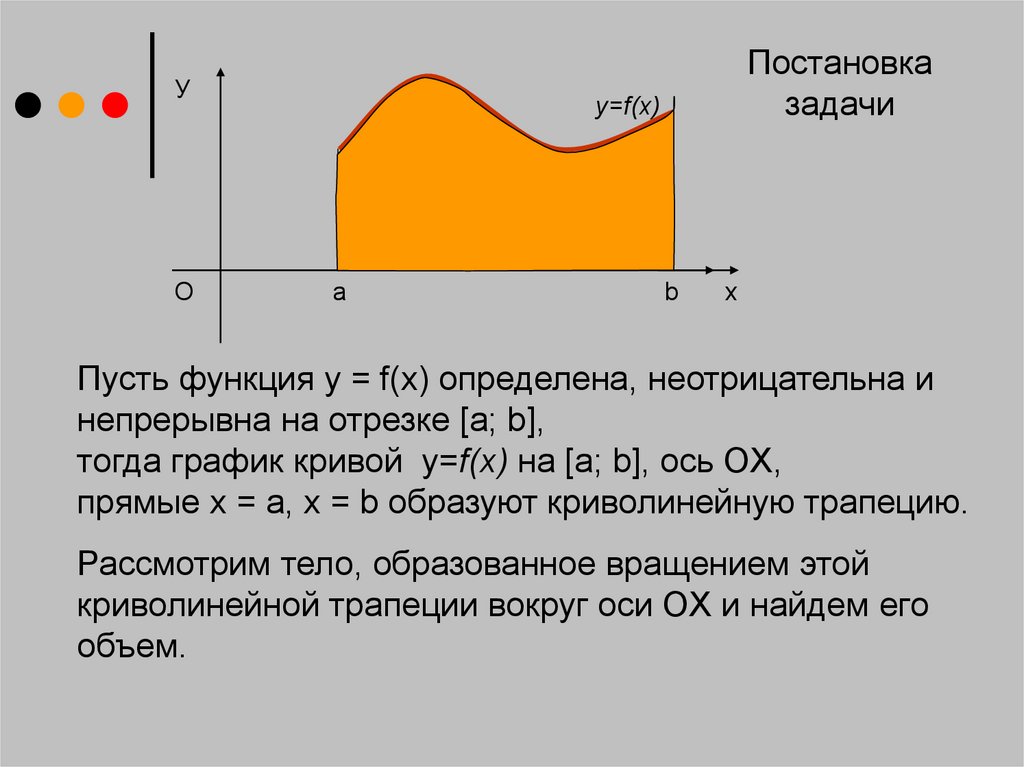
УO
Постановка
задачи
y=f(x)
a
b
х
Пусть функция y = f(x) определена, неотрицательна и
непрерывна на отрезке [a; b],
тогда график кривой у=f(x) на [a; b], ось OX,
прямые x = a, x = b образуют криволинейную трапецию.
Рассмотрим тело, образованное вращением этой
криволинейной трапеции вокруг оси OX и найдем его
объем.
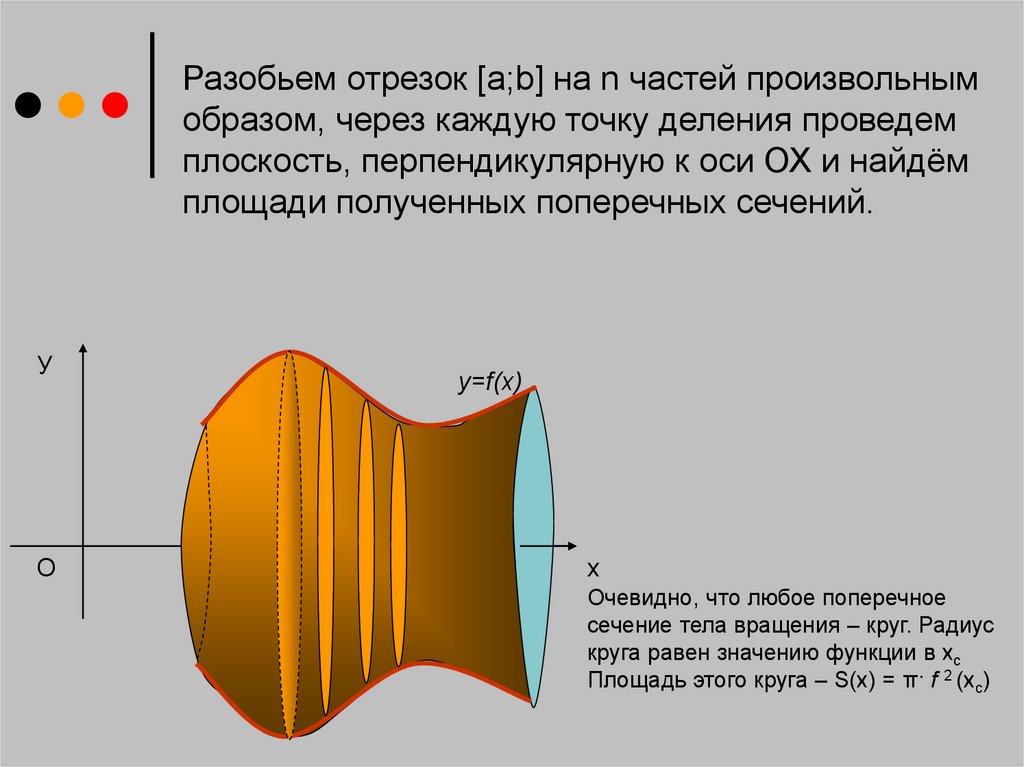
3.
Разобьем отрезок [a;b] на n частей произвольнымобразом, через каждую точку деления проведем
плоскость, перпендикулярную к оси ОХ и найдём
площади полученных поперечных сечений.
У
O
y=f(x)
х
Очевидно, что любое поперечное
сечение тела вращения – круг. Радиус
круга равен значению функции в хс
Площадь этого круга – S(x) = π· f 2 (xс)
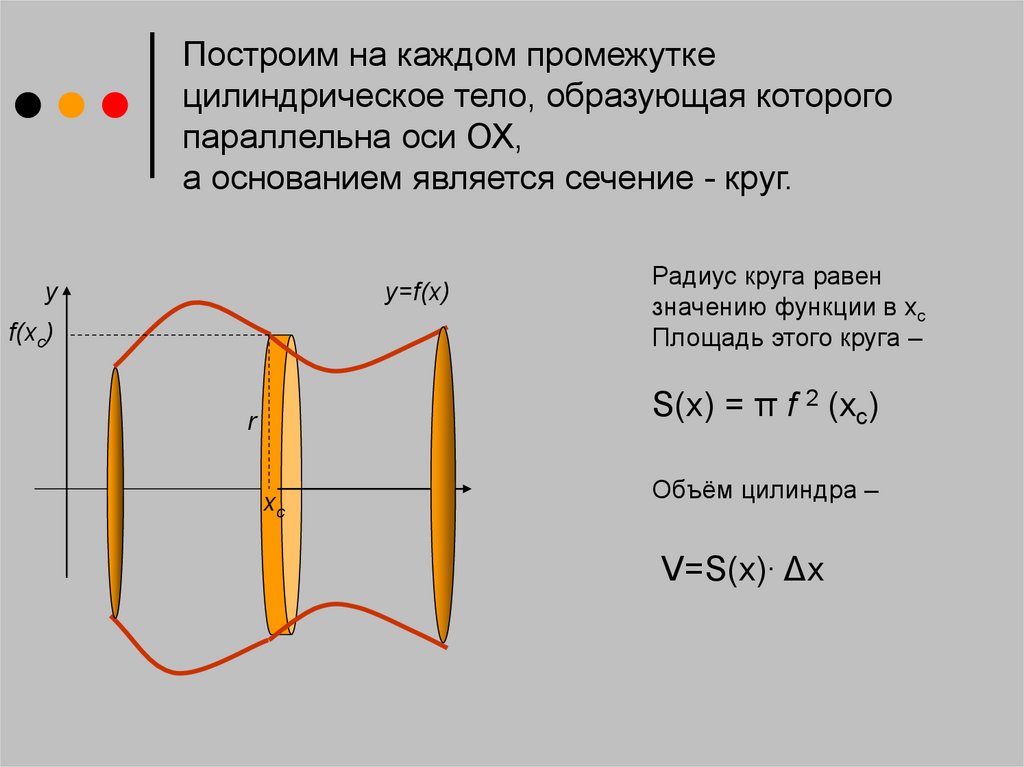
4.
Построим на каждом промежуткецилиндрическое тело, образующая которого
параллельна оси ОХ,
а основанием является сечение - круг.
y
y=f(x)
f(xс)
Радиус круга равен
значению функции в хс
Площадь этого круга –
S(x) = π f 2 (xс)
r
xс
Объём цилиндра –
V=S(x)∙ Δx
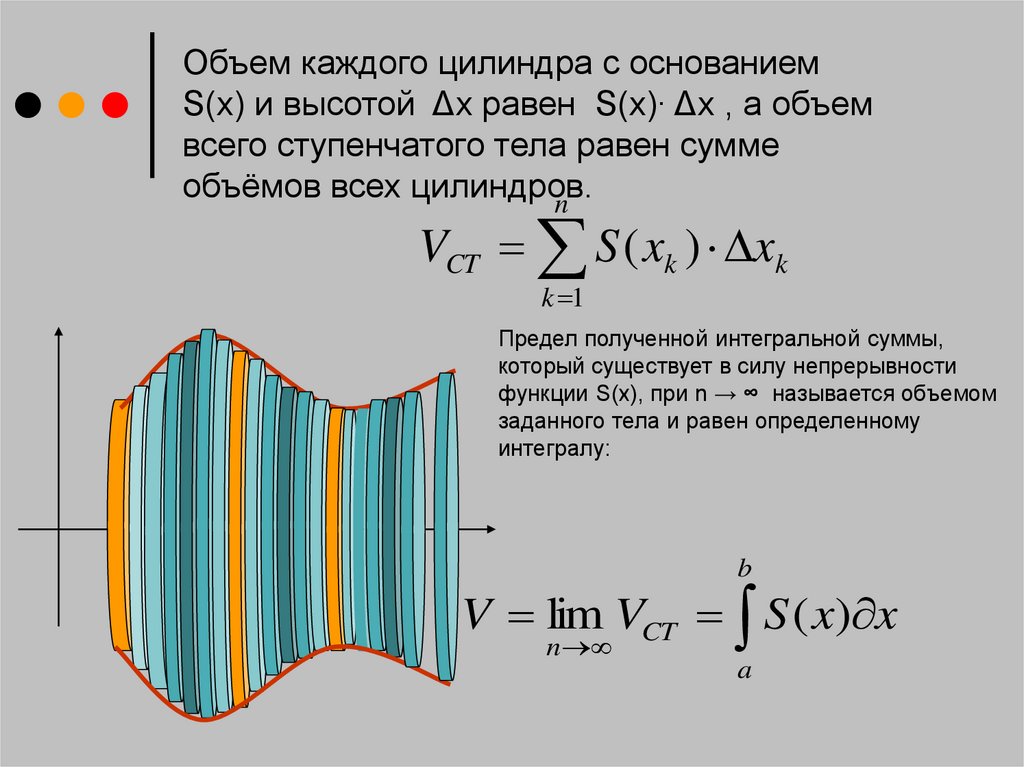
5.
Объем каждого цилиндра с основаниемS(x) и высотой Δx равен S(x)∙ Δx , а объем
всего ступенчатого тела равен сумме
объёмов всех цилиндров.
n
VCT S ( xk ) xk
k 1
Предел полученной интегральной суммы,
который существует в силу непрерывности
функции S(x), при n → ∞ называется объемом
заданного тела и равен определенному
интегралу:
b
V lim VCT S ( x) x
n
a
6.
Предел полученной интегральной суммы, при n → ∞равен определенному интегралу:
n
b
k 1
a
V lim S ( x) x S ( x) x
n
Тогда объем тела вращения вокруг оси ОХ:
b
b
b
a
a
a
V S ( x) x f 2 ( x) x f 2 ( x) x
Если тело образовано вращением криволинейной
трапеции, образованной функцией у=f(x) на отрезке
[a;b],вокруг оси ОХ, то его объём можно найти по
формуле:
y=f(x)
b
y
V f ( x) x
2
x
a
7.
bV f 2 ( x) x
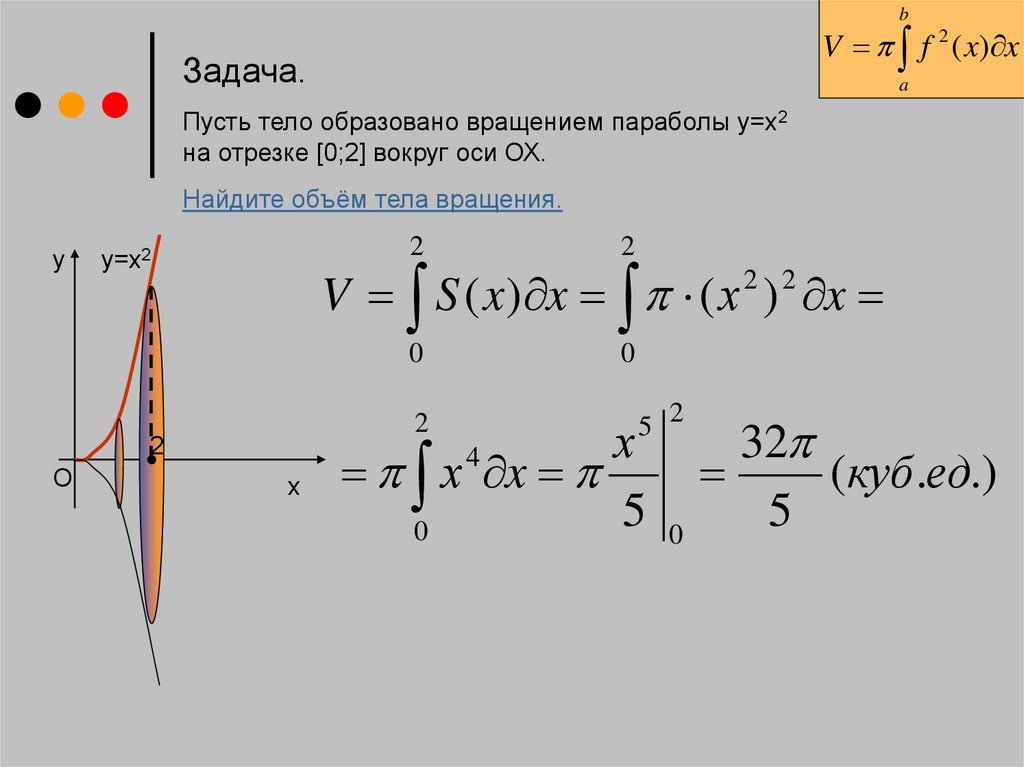
Задача.
a
Пусть тело образовано вращением параболы у=х2
на отрезке [0;2] вокруг оси ОХ.
Найдите объём тела вращения.
у
2
у=х2
2
V S ( x) x ( х ) x
2 2
0
5 2
2
2
О
0
х
х
х x
5
0
4
0
32
(куб .ед.)
5
8.
bV f 2 ( x) x
Задача.
a
Пусть тело образовано вращением функции у=0,5x
на отрезке [0;4] вокруг оси ОХ.
Найдите объём тела вращения.
y
y 0,5 х
4
V (0,5х) x
2
O
4
x
0
0,25x
3
3
4
0
16
( кв.ед.)
3
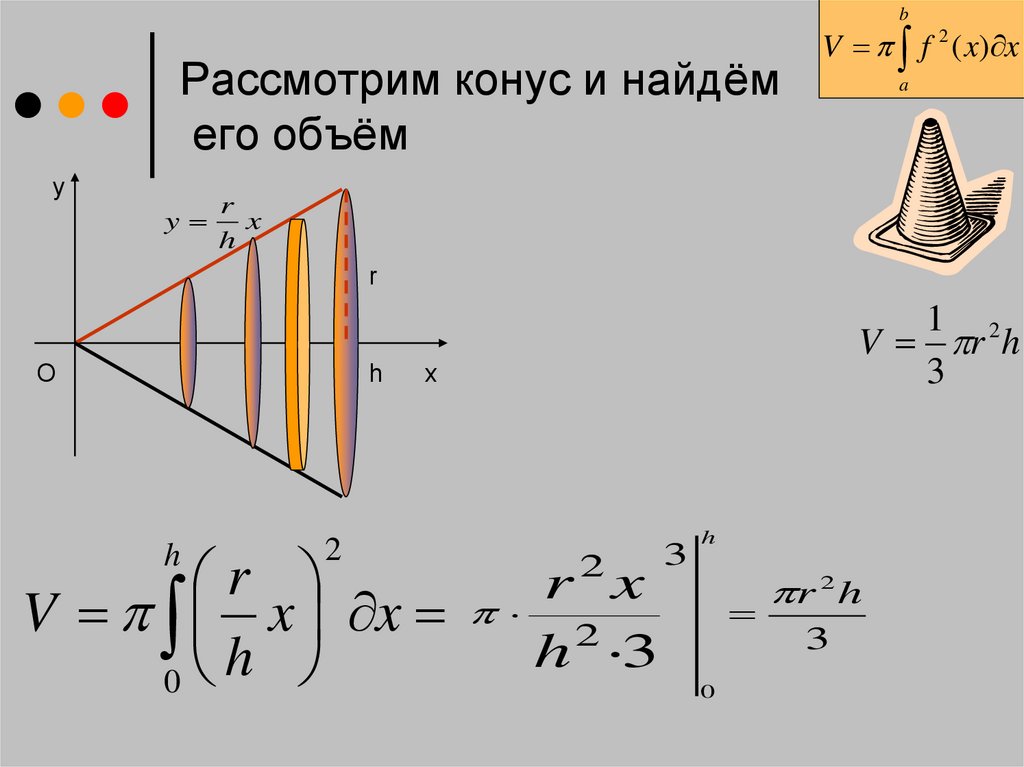
9. Рассмотрим конус и найдём его объём
bРассмотрим конус и найдём
его объём
y
y
V f 2 ( x) x
a
r
x
h
r
O
h
2
x
r
V x x
h
0
h
1 2
V r h
3
2
r x
2
h 3
3
h
0
r 2 h
3
10. Рассмотрим усечённый конус и найдём его объём
bV f 2 ( x) x
Рассмотрим усечённый
конус и найдём его объём
y
y
R r
x r
h
R
h
R r
V
x r x
h
0
2
h
r
O
x
R r
x r
h
h
R r
3
h
3( R r )
a
R
3
r
3
3 h
0
1
3
h( R Rr r )
2
2
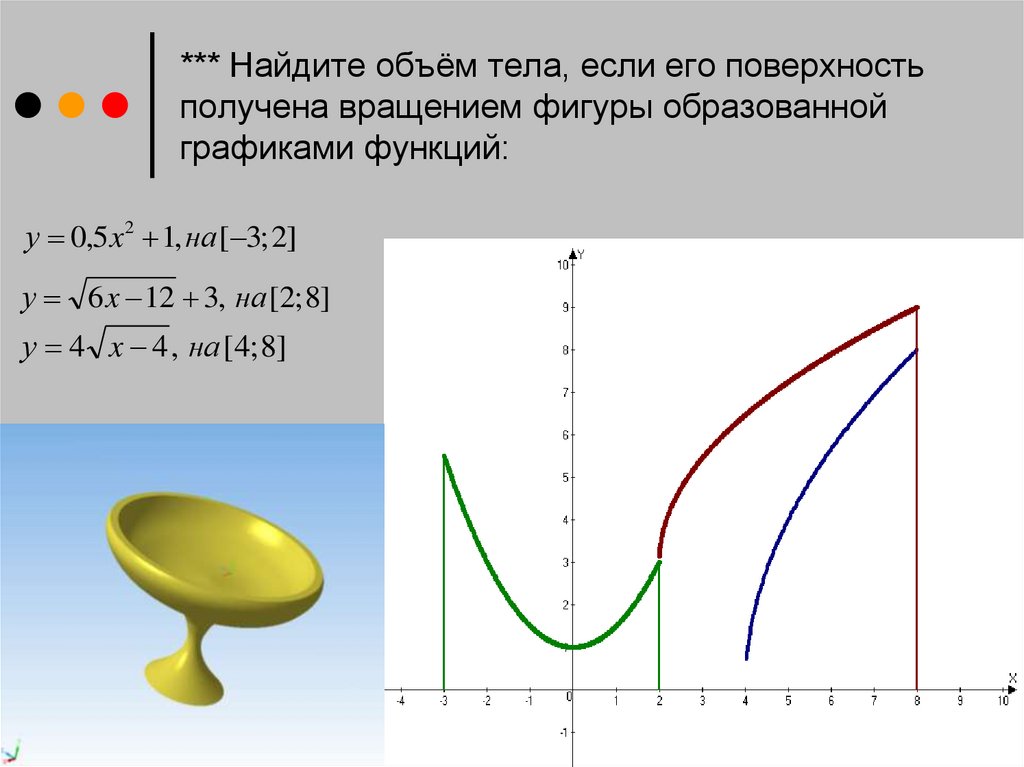
11. *** Найдите объём тела, если его поверхность получена вращением фигуры образованной графиками функций:
у 0,5x 2 1, на [ 3; 2]у 6 x 12 3, на [2; 8]
у 4 x 4 , на [4; 8]
12. Вычисление определённых интегралов
bV f 2 ( x) x
a
V Vоснования Vчаши Vвыемки
2
2
Vоснования 0,5 x 2 1 x (0,25x 4 x 2 1) x
30 125 куб .ед.
3
3
8
Vчаши
2
8
2
8
6 x 12 3 x (6 x 12 6 6 x 12 9) x
2
306 куб .ед.
2
8
Vвыем ки 4 4 x 4 x 16(4 x 4) x 128 куб .ед.
2
4
Vкубка 208 125 654.4куб .ед
4
13.
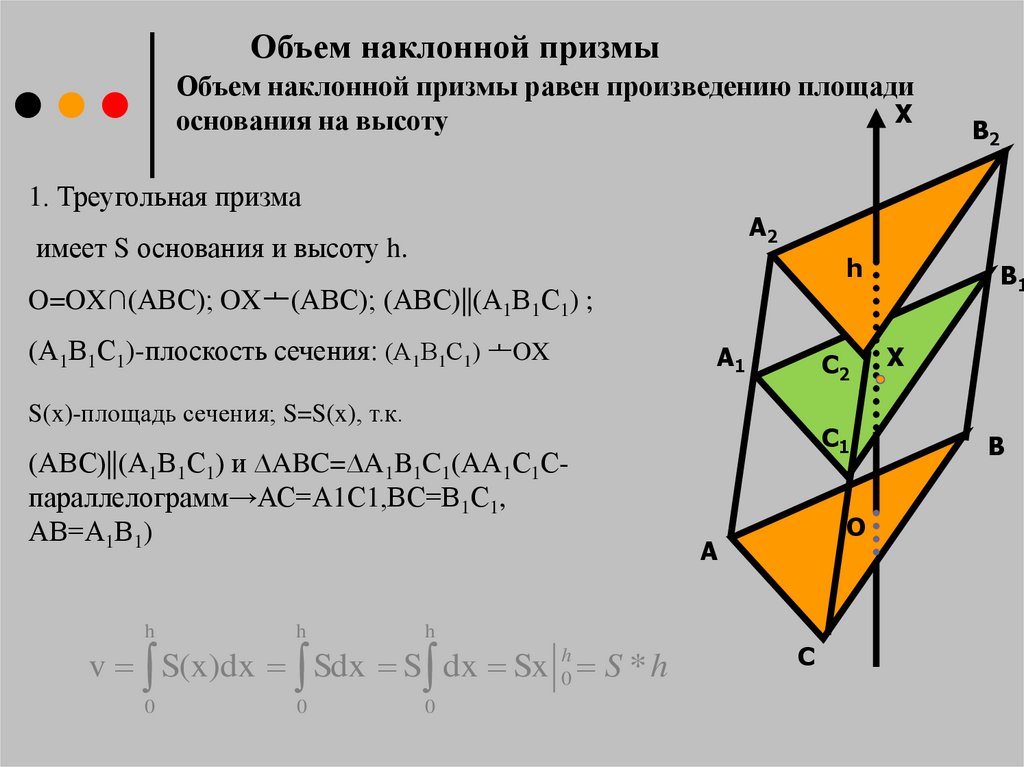
Объем наклонной призмыОбъем наклонной призмы равен произведению площади
X
основания на высоту
1. Треугольная призма
B2
A2
имеет S основания и высоту h.
h
B1
O=OX∩(АВС); OXᅩ(АВС); (АВС)||(А1В1С1) ;
(А1В1С1)-плоскость сечения: (А1В1С1) ᅩOX
A1
C2
S(x)-площадь сечения; S=S(x), т.к.
(АВС)||(А1В1С1) и ∆ABC=∆A1B1C1(АА1С1Спараллелограмм→АС=А1С1,ВС=В1С1,
АВ=А1В1)
h
h
h
0
0
0
v S(x)dx Sdx S dx Sx 0h S * h
C1
O
A
C
X
B
14.
S3S2
S1
2. Наклонная призма с многоугольником
в основании
V=V1+V2+V3=
h
=S1*h+S2*h+S3*h=
=h(S1+S2+S3)=S*h
Объем наклонной призмы равен произведению бокового ребра
на площадь перпендикулярного ребру сечения
15.
№ 676 Найти объем наклонной призмы, у которойоснованием является треугольник со сторонами
10см,10см,12см, а боковое ребро равное 8см, составляет с
плоскостью основания угол 600
Дано: АВСА1В1С1- наклонная прямая призма. <В1ВК=600 ,
ВС=10см, АВ=10см, АС=12см, ВВ1=8см.
Найти:Vпризмы=?
Решение:
V= SАВС* h , Sосн.=√р(р-а)(р-b)(р-с) - формула Герона
Sосн.=√16*6*4*6 = 4*2*6 = 48 (см2)
В1
Треугольник ВВ1Н- прямоугольный,
так как В1Н –высота В1Н=ВВ1*cos 600 С1
А1
В1Н=8 * √3/2 = 4√3 (см)
В
V=4√3 *48=192√3 (см3)
Н
Ответ: Vпр. = 192√3
(см3)
С
К
А
16.
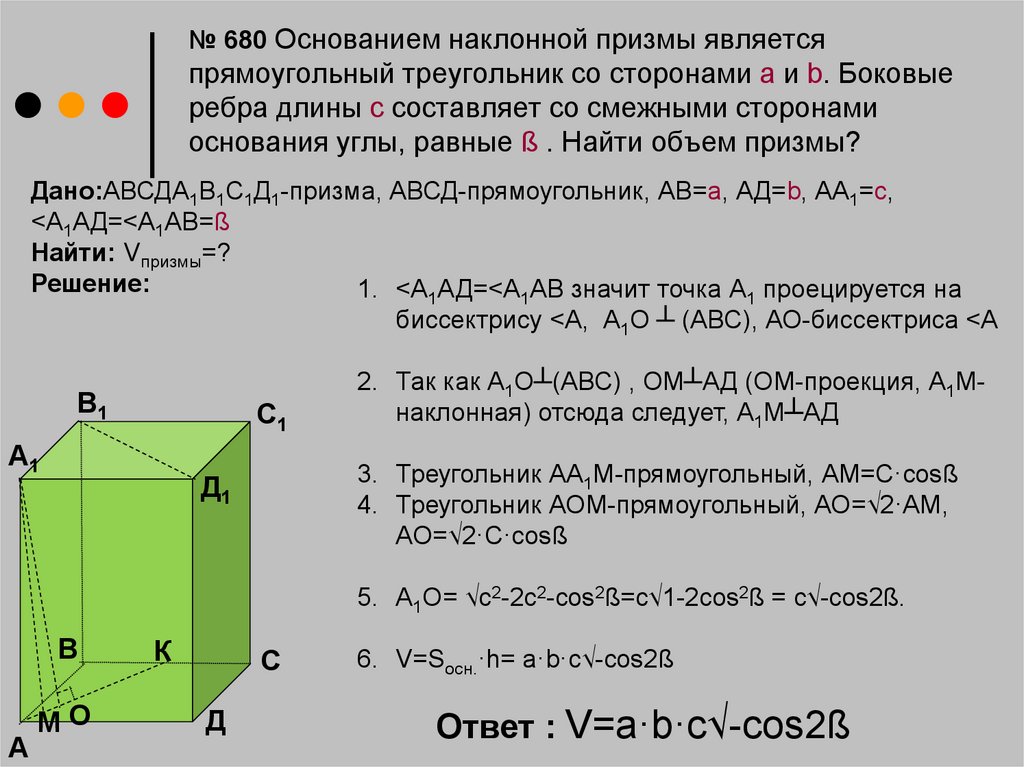
№ 680 Основанием наклонной призмы являетсяпрямоугольный треугольник со сторонами а и b. Боковые
ребра длины с составляет со смежными сторонами
основания углы, равные ß . Найти объем призмы?
Дано:АВСДА1В1С1Д1-призма, АВСД-прямоугольник, АВ=а, АД=b, АА1=с,
<А1АД=<А1АВ=ß
Найти: Vпризмы=?
Решение:
1. <А1АД=<А1АВ значит точка А1 проецируется на
биссектрису <А, А1О ┴ (АВС), АО-биссектриса <А
В1
С1
А1
2. Так как А1О┴(АВС) , ОМ┴АД (ОМ-проекция, А1Мнаклонная) отсюда следует, А1М┴АД
3. Треугольник АА1М-прямоугольный, АМ=С·cosß
4. Треугольник АОМ-прямоугольный, АО=√2·АМ,
АО=√2·С·сosß
Д1
5. А1О= √с2-2с2-cos2ß=с√1-2cos2ß = с√-cos2ß.
В
А
МО
К
С
Д
6. V=Sосн.·h= а·b·c√-cos2ß
Ответ : V=а·b·c√-cos2ß
17.
Свойство объемов №1Равные тела имеют равные объемы
Свойство объемов №2
Если тело составлено из нескольких тел, то
его объем равен сумме объемов этих тел.
Свойство объемов №3
Если одно тело содержит другое, то объем
первого тела не меньше объема второго.








 mathematics
mathematics








