Similar presentations:
Вычисление объемов тел вращения
1. Вычисление объемов тел вращения
2.
Задача на нахождение объема тела вращенияy f (x)
У
O
х
a
b
Пусть функция y = f(x) определена, неотрицательна и
непрерывна на отрезке [a; b],
тогда график кривой у=f(x) на [a; b], ось OX,
прямые x = a, x = b образуют криволинейную трапецию.
Рассмотрим тело, образованное вращением этой
криволинейной трапеции вокруг оси OX и найдем его объем.
3.
Разобьем отрезок [a;b] на n частей произвольным образом, черезкаждую точку деления проведем плоскость, перпендикулярную к оси
ОХ и найдём площади полученных поперечных сечений.
Эти плоскости разбивают тело на п частей
1. Очевидно, что любое поперечное
сечение тела вращения – круг.
у
y f (x)
2.Радиус этого круга равен
значению функции в точке
3. Площадь этого круга
равна
O
a
b
х
S ( x) f 2 ( xk )
xk
4.
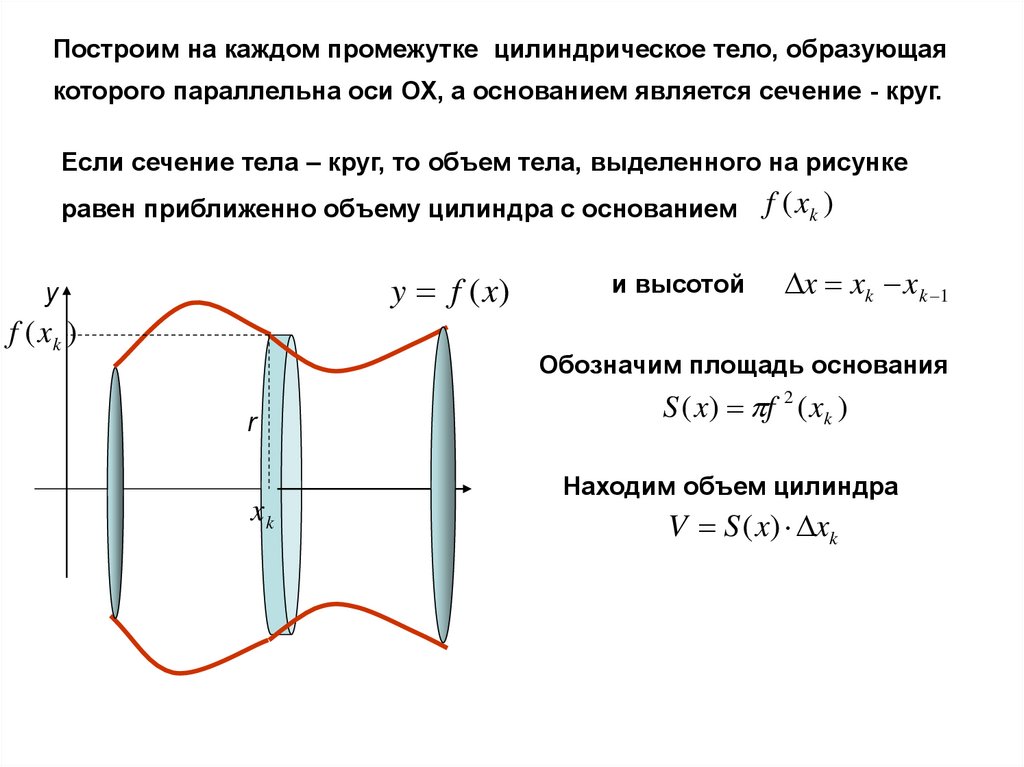
Построим на каждом промежутке цилиндрическое тело, образующаякоторого параллельна оси ОХ, а основанием является сечение - круг.
Если сечение тела – круг, то объем тела, выделенного на рисунке
равен приближенно объему цилиндра с основанием
y f (x)
y
f ( xk )
и высотой
f ( xk )
x xk x k 1
Обозначим площадь основания
r
xk
S ( x) f 2 ( xk )
Находим объем цилиндра
V S ( x) xk
5.
объем всего тела равен сумме объёмов всех цилиндров.V S ( x1 ) x1 ... S ( xk ) xk ... S ( xn ) xn
Приближенное значение V объема тела тем точнее, чем больше п
и, следовательно, меньше
xk
Предел полученной интегральной
суммы, который существует в силу
непрерывности функции S(x), при n → ∞
называется объемом заданного тела и
равен определенному интегралу:
b
V lim VCT S ( x) x
n
a
6.
Предел полученной интегральной суммы, при n → ∞ равен определенномуинтегралу:
n
b
k 1
a
V lim S ( x) x S ( x) x
n
Тогда объем тела вращения вокруг оси ОХ:
b
b
b
a
a
a
V S ( x) x f 2 ( x) x f 2 ( x) x
•Если тело образовано вращением криволинейной трапеции,
образованной функцией у=f(x) на отрезке [a;b],вокруг оси ОХ, то его
объём можно найти по формуле:
y
y=f(x)
b
V f ( x) x
2
x
a
7.
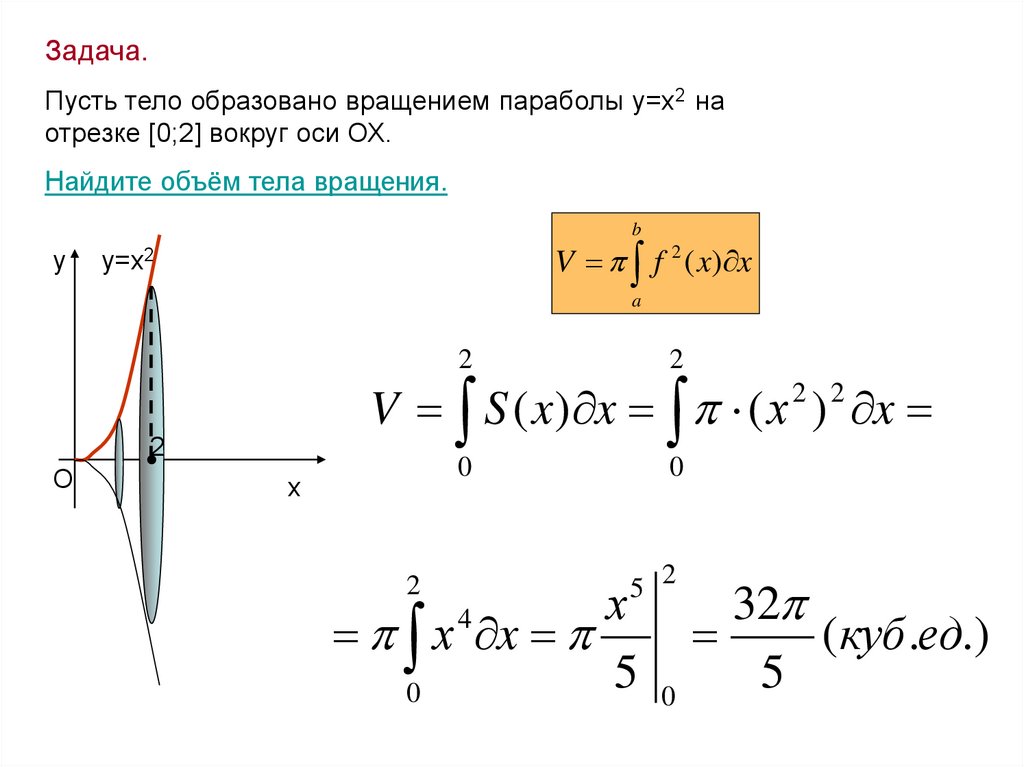
Задача.Пусть тело образовано вращением параболы у=х2 на
отрезке [0;2] вокруг оси ОХ.
Найдите объём тела вращения.
b
у
V f 2 ( x) x
у=х2
a
2
2
V S ( x) x ( х ) x
2 2
2
О
0
х
0
5 2
2
х
х x
5
0
4
0
32
(куб .ед.)
5
8.
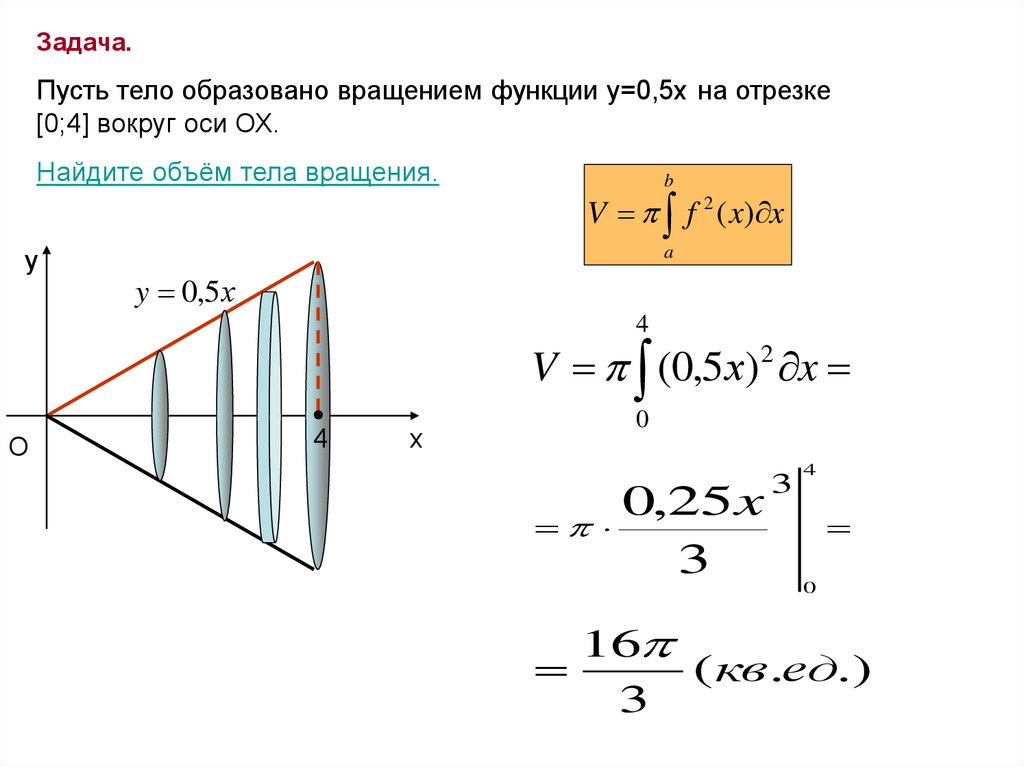
Задача.Пусть тело образовано вращением функции у=0,5x на отрезке
[0;4] вокруг оси ОХ.
Найдите объём тела вращения.
b
V f 2 ( x) x
y
a
y 0,5 х
4
V (0,5х) x
2
O
4
x
0
0,25x
3
3
4
0
16
( кв.ед.)
3
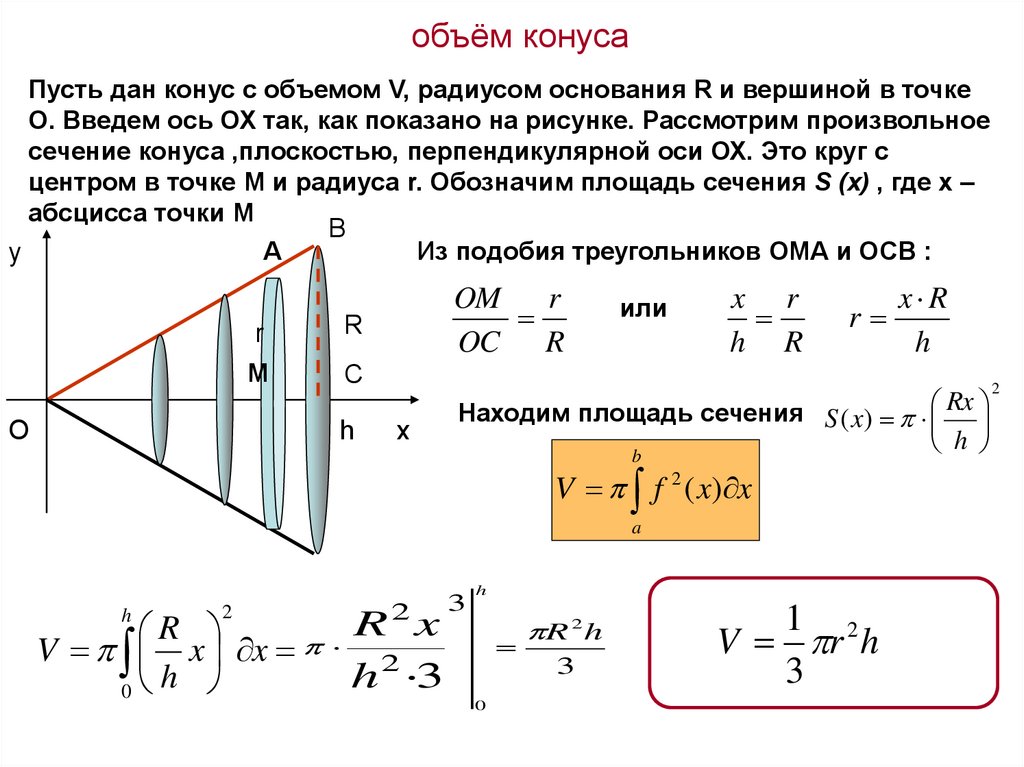
9. объём конуса
Пусть дан конус с объемом V, радиусом основания R и вершиной в точкеО. Введем ось ОХ так, как показано на рисунке. Рассмотрим произвольное
сечение конуса ,плоскостью, перпендикулярной оси ОХ. Это круг с
центром в точке М и радиуса r. Обозначим площадь сечения S (x) , где х –
абсцисса точки М
B
А
Из подобия треугольников ОМА и ОСВ :
y
O
r
R
М
C
h
OM
r
OC R
x
или
x r
h R
r
Находим площадь сечения S ( x) Rx
h
b
V f 2 ( x) x
a
2
R
x
R
V x x 2
h 3
h
0
h
2
x R
h
3
h
0
R 2 h
3
1 2
V r h
3
2





 mathematics
mathematics








