Вычисление объемов геометрических тел с помощью определенного интеграла

1. Вычисление объемов геометрических тел с помощью определенного интеграла.

2.

1612 г.
Австрия
город Линц.

3.

«Новая
стереометрия
винных бочек»,
1615 г.
Иоганн Кеплер
(1571 – 1630)

4.

Иоганн Кеплер
1571 – 1630
«Новая стереометрия винных бочек»
Рассказывают, что когда Кеплер покупал
вино для свадьбы, он был изумлен тем,
как торговец определял вместимость
бочки. Продавец брал палку, на которой
были нанесены деления, и с ее помощью
определял расстояние от наливного
отверстия до самой дальней точки
бочки. Проделав это одно измерение, он
сразу же говорил, сколько литров вина в
данной бочке.

5.

Кеплера заинтересовало, насколько
точно торговец определял объем бочки
при помощи всего одного измерения. Так
ученый первым обратил внимание на
класс задач, исследование которых
привело к созданию интегрального
исчисления.

6.

Вначале Кеплер нашел формулу для
вычисления объема бочки, а затем — и
других тел вращения (всего 92),
которым он дал названия: «лимон»,
«яблоко», «груша», «айва», «слива»,
«земляника», «турецкая чалма» и т. п.
Для нахождения объемов этих
неправильных тел он применил метод
«исчерпывания», заполняя тела
фигурами, объемы которых поддавались
вычислению. Одновременно он разбивал
тело на множество элементарных
частей.

7.

Находя объем тела как сумму
элементарных объемов, заполнявших
тело, Кеплер часто употреблял
латинское выражение Summa omnium —
сумма всех. Как известно, один из
создателей интегрального исчисления,
Лейбниц, ввел знак интеграла
(удлиненная буква S) именно для
сокращенной записи выражения Summa
omnium.

8.

Написанная Кеплером и изданная в 1615
году «Новая стереометрия винных
бочек» положила начало целому ряду
исследований, которые привели к
созданию Ньютоном и Лейбницем
дифференциального и интегрального
исчисления. Математика переменных
величин заняла ведущее место в
системе математических знаний.

9.

Если функция f(x) непрерывна на
промежутке I числовой оси, содержащей
точки х=а и х=b, то разность значений
F(b)-F(a) (где F(x) - первообразная f(x) на I)
называется определенным интегралом
от функции f(x) от a до b.
b
f ( x)dx F (b) F (a) F ( x)
b
a
a
формула Ньютона-Лейбница.

10.

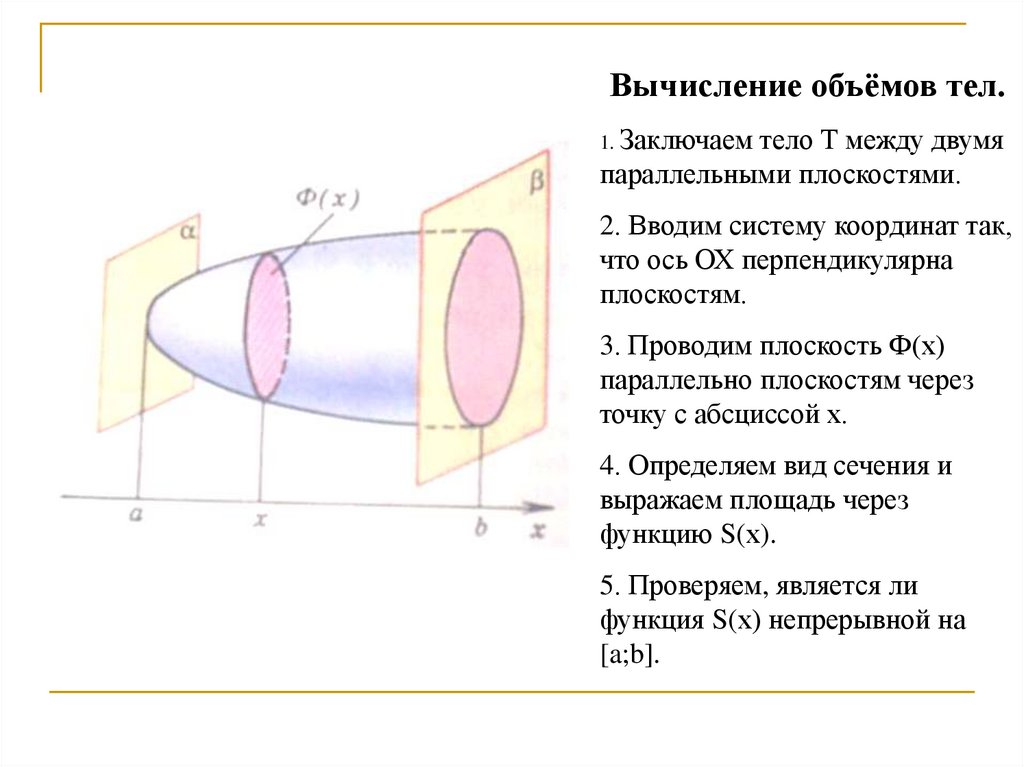
Вычисление объёмов тел.
1. Заключаем
тело Т между двумя
параллельными плоскостями.
2. Вводим систему координат так,
что ось ОХ перпендикулярна
плоскостям.
3. Проводим плоскость Ф(х)
параллельно плоскостям через
точку с абсциссой х.
4. Определяем вид сечения и
выражаем площадь через
функцию S(х).
5. Проверяем, является ли
функция S(х) непрерывной на
[a;b].

11.

6. Разбиваем [a;b] на n - равных
отрезков точками а = х0, х1, х2,
…хn=b
и проводим через хi плоскости
перпендикулярно ОХ.
7. Плоскости разбивают тело Т на
n- тел Т1, Т2, Т3,... Тn с
основаниями Ф(хi) и высотой
xi= (b - a)/n
8. V Vn= (S(x1) + S(x2) +…+ S(xn) ) xi= =(S(x1) + S(x2) +…+
S(xn))(b - a)/n. При n , Vn V, поэтому V
Vn
lim
b
но lim V S ( x)dx
n
n
a
9.
b
V
S ( x)dx
a
n

12.

АЛГОРИТМ ВЫЧИСЛЕНИЯ ОБЪЁМОВ
ГЕОМЕТРИЧЕСКИХ ТЕЛ С ПОМОЩЬЮ
ОПРЕДЕЛЁННОГО ИНТЕГРАЛА.
1. Ввести систему координат так, что ось ОХ
перпендикулярна основанию геометрического тела.
2. Найти пределы интегрирования а и b.
3. Провести сечение плоскостью перпендикулярно оси
ОХ через точку с абсциссой х.
Определить вид сечения, задать формулой его
площадь как функцию S(X).
4. Проверить
b непрерывность функции S(X) на [a;b].
5.
V
S ( x)dx
a

13.

Задача 1.Найти объём наклонной треугольной призмы с
основанием S и высотой h.
1. Введём ось ОХ перпендикулярно
В
основаниям призмы.
Х
А
2. (АВС) OX=a, a=0, (A1B1C1) OX=b, b=h
h *
3. Проведём плоскость
С
A
B
перпендикулярно ОХ через точку с
абсциссой х.
*
x
x
А2В2С2-треугольник, равный
C
основаниям.
В
Площадь А2В2С2 равна S.
А
0 *
1
1
2
2
4. S(x) непрерывна на [0;h]
h
h
5.
С
V S ( x )dx Sdx Sx 0h Sh 0 Sh
0
0
Ответ: V=Sh
2
1