Similar presentations:
Тепломассообмен. Теплопроводность через плоские и цилиндрические стенки
1. Тепломассообмен 2
Теплопроводность через плоскиеи цилиндрические стенки
2. Теплопроводность через однослойную плоскую стенку
tConst
tc1
h
q
x
0
dx
tc2
x
3. Дифференциальное уравнение теплопроводности (частный случай)
Ранее мы получили общий видqv
t
2
дифференциального уравнения
(1)
a t
c .
теплопроводности:
В частном случае, для стационарного процесса t / 0 ;
при отсутствии внутренних источников теплоты q 0:
v
из (1) при a 0 следует: 2t 0,
2
2
2
t
t
t
или развернутое выражение
0
2
2
2
x y z
оператора Лапласа:
.
(2)
Для бесконечной пластины: h ;b , то есть:
2t / y2 0; 2t / z2 0 .
Дифференциальное уравнение
d 2t
0 .
теплопроводности запишется в виде:
(3)
2
dx
4. Условия однозначности
Для рассматриваемого случая добавляемусловия однозначности:
● Геометрические: вертикальная пластина h ;b ,
● Физические: Const;
● Начальные: для стационарного процесса не требуются,
● Граничные условия I рода: при x 0 t t Const;
Найти:
t f ( x) ?;q ?
при
c1
x t tc2 Const.
После первого интегрирования
дифференциального уравнения (3) имеем:
После разделения переменных в (5):
dt
c1;
dx
dt c1dx;
(4)
(5)
(6)
5. Удельный тепловой поток
t c1x c2.После 2-го интегрирования:
Для определения констант интегрирования
подставляем (4) в (7):
при x 0 t
при
x
(7)
tc1 c2 ;
t tc2 c1 c2 c1 tc1;
откуда с учетом (5) имеем:
По закону Фурье:
c1
dt
.
dx
(9)
dt
q
dt
.
q ; откуда градиент
dx
dx
t t
q
Подставляя (10) в (9), получим:
q (tc1 tc2 ),
tc2 tc1
(8)
c2
c1
(10)
, откуда:
или в форме закона Ома:
q
t
.
R
(11)
6. Теплопроводность через трехслойную плоскую стенку
21
t
3
tc1
t'
q
t"
tc2
0
1
2
3
x
7. Термическое сопротивление тепло-проводности 3-слойной плоской стенки
Термическое сопротивление теплопроводности 3-слойной плоской стенкиДля стационарного теплового режима q idem :
в первом слое
1
(tc1 t ');tc1 t ' q 1 ;t ' tc1 q 1 ;
1
1
1
q 2 (t ' t ");t ' t " q 2 ;
2
2
q 3 (t " tc 2 );t " tc 2 q 3 ;t " tc 2 q 3 .
3
3
3
q
во втором слое
в третьем слое
Сложив правые и левые части этих трех выражений, получим:
1 2 3
или в форме закона Ома –
t
tc1 tc 2 q(
1 2 3
) qR,
q
где термическое сопротивление теплопроводности
1 2
трехслойной плоской стенки, (м2К)/Вт :
R
1 2
3
3
.
R
,
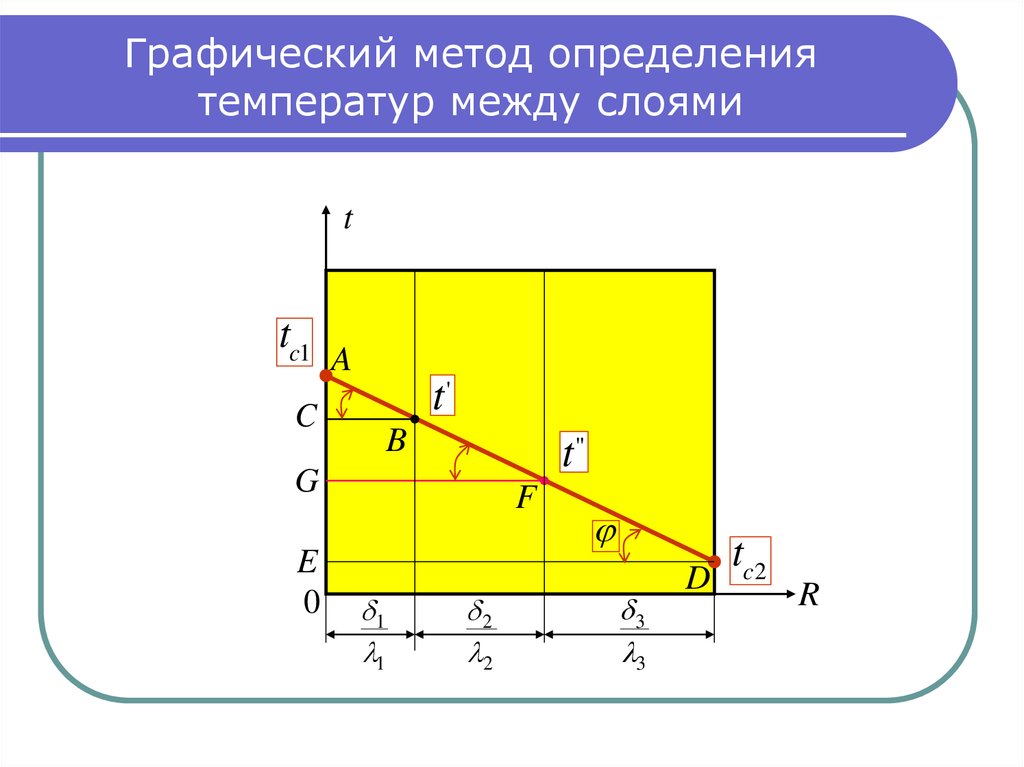
8. Графический метод определения температур между слоями
ttc1
A
t'
C
B
t"
G
E
0
F
1
1
2
2
3
3
D
tc2
R
9. Определение температур между слоями
Треугольники АBC и ADE подобны между собой по равенствутрех углов. Из их подобия следует:
AC AE
tg
,
BC DE
то есть
или:
tg
tc1 t '
1
1
tc1 tc2
1 2 3
1 2 3
q,
AC tc1 t ' , откуда находится температура t ' .
Аналогично, из подобия треугольников AFG и ADE:
AG tc1 t".
Отсюда находится температура
t".
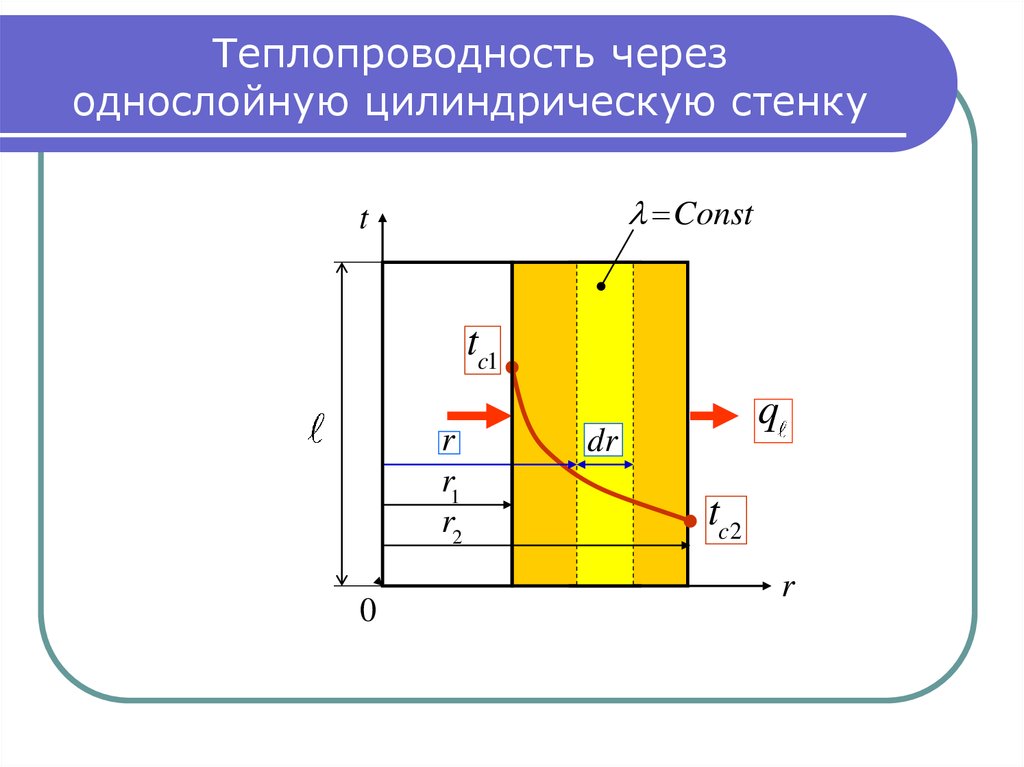
10. Теплопроводность через однослойную цилиндрическую стенку
Constt
tc1
r
r1
r2
0
q
dr
tc2
r
11. Дифференциальное уравнение тепло-проводности для цилиндрической стенки
Дифференциальное уравнение теплопроводности для цилиндрической стенкиОбщее выражение дифференциального уравнения
qv
теплопроводности: t
2
a t
c
.
(1)
Для стационарного процесса
t / 0;
при отсутствии внутренних источников теплоты qv 0,
с учетом этих условий уравнение (1) примет вид a 2t 0 .
Но a 0 , тогда частный вид дифференциального уравнения
теплопроводности: 2t 0.
Или через развернутое выражение оператора Лапласа:
2
2
2
t
1
t
1
t
t
2 2 2 0 .
2t 2
r r r r z
(2)
12. Условия однозначности
Добавляем условия однозначности:● Геометрические условия:
r2 (бесконечная цилиндрическая стенка);
● Физические условия: Const;
● Начальные условия: для стационарного процесса не
требуются;
● Граничные условия I рода:
при
при
r r1
t tc1 Const;
r r2
t tc2 Const.
(3)
13. Преобразование дифференциального уравнения
В соответствии с геометрическими условиями однозначности,в бесконечной цилиндрической стенке температура не изменяется по координатам z и , тогда уравнение (2) примет вид:
(4).
Найти: t f (r ) ?;Q ?.
2
d t 1 dt
0,
2
dr r dr
Представим дифференциальное уравнение (4) в виде:
d dt 1 dt
( ) ( ) 0,
dr dr r dr
Умножим его на:
dr
dt
d
(
)
dt и получим
dr dr 0;
( )
dr окончательно dt
r
dr
14. Интегрирование
После первого интегрирования имеем:n(
dt
) n(r ) n(c1).
dr
Или:
dt
r c1.
После потенцирования:
dr
Разделяем переменные в (5):
после второго интегрирования:
dt
n( r ) n(c1).
dr
(5)
dr
;
r
t c1 n(r) c2
- это логарифмическая зависимость
dt c1
t f (r) .
(6)
15. Определение констант интегрирования
Подставляем граничные условия (3) в (6):при
r r1
r r2
Получим:
t tc1 c1 n(r1) c2;
t tc2 c1 n(r2 ) c2.
r
d
tc1 tc2 c1[ n(r1) n(r2 )] c1 n( 1 ) c1 n( 1 ).
r2
d2
Находим отсюда константу интегрирования, которая
с учетом (5):
t t
dt
c1 c1 c2 r.
(7)
n(d 2 / d1 ) dr
Q (8)
По закону Фурье: Q F dt 2 r dt , или dt
r
.
dr
dr
dr
2
16. Тепловой поток
Подставляем (8) в (7):tc1 tc2
Q
,
n(d 2 / d1 )
2
откуда: полный и удельный тепловые потоки
(9)
Q (tc1 tc2 )
Q
, Bт.
q
, Вт / м.
d
1
d
1
n( 2 )
n( 2 )
2
d1
2
d1
Или в форме закона Ома: q t .
(10)
R
Здесь R 1 n( d 2 ) (11) - линейное термическое
2
d1
сопротивление теплопроводности
(tc1 tc2 )
1-слойной цилиндрической стенки, (мК)/Вт.
17. Теплопроводность через трехслойную цилиндрическую стенку
21
t
3
tc1
t'
r1
r2
r3
r4
0
q
t"
tc2
r
18. Линейное термическое сопротивление теплопроводности
Для всех слоев при стационарном тепловом режиме: qТогда падения температур в каждом слое:
t ' t " q 1 n d3 ;
tc1 t ' q 1 n d 2 ;
2 1
2 2
d1
d2
2 3
d3
d
d
d
q
1
1
1
n 2
n 3
n 4) R ;
2 1 d1 2 2 d 2 2 3 d3
q
(
тогда линейное термическое сопротивление
трехслойной цилиндрической стенки, (мК)/Вт
и температуры между слоями С:
d
d
d
1
1
1
R
n 2
n 3
n 4
2 1 d1 2 2 d 2 2 3 d3
;
R
t " tc2 q 1 n d 4 .
Сложив левые и правые части этих уравнений, получим:
tc1 tc 2
t
t ' tc1 q 1 n d 2 ;
2 1
d1
t " tc2 q 1 n d 4 .
2 3 d3
.
















 physics
physics








