Теплотехника. Теплопроводность через плоскую стенку

1. Теплотехника

Теплопроводность через плоскую
стенку

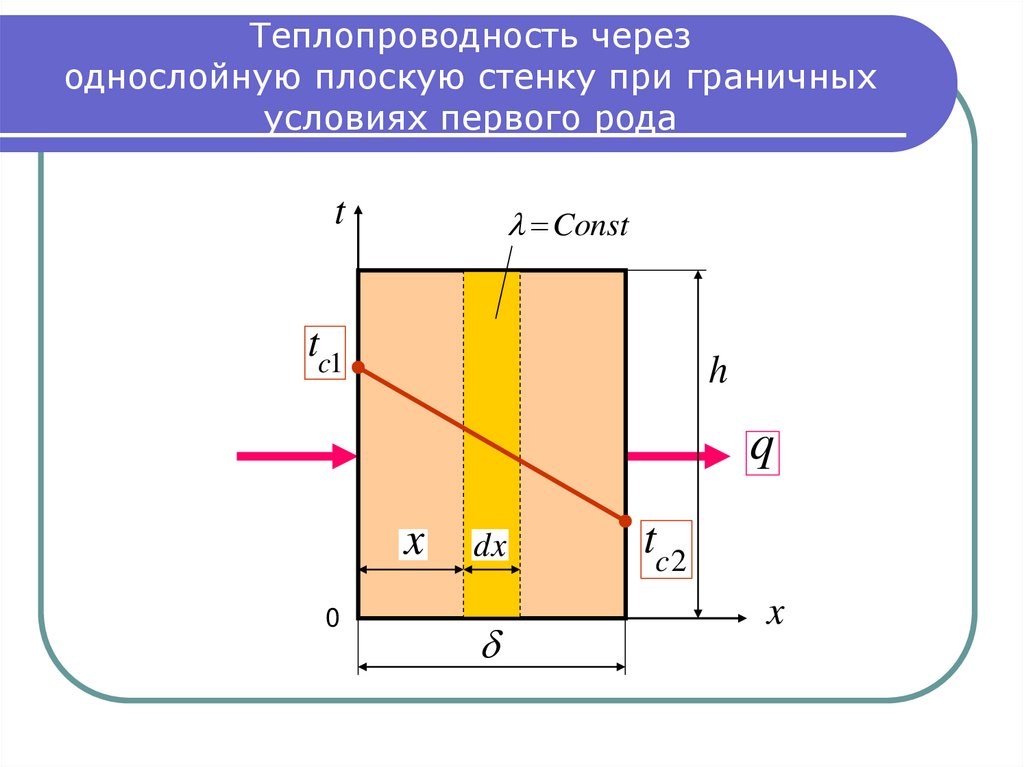
2. Теплопроводность через однослойную плоскую стенку при граничных условиях первого рода

t
Const
tc1
h
q
x
0
dx
tc2
x

3. Дифференциальное уравнение теплопроводности (частный случай)

Ранее мы получили общий вид
qv
t
2
дифференциального уравнения
(1)
a t
c .
теплопроводности:
В частном случае, для стационарного процесса t / 0 ;
при отсутствии внутренних источников теплоты q 0:
v
из (1) при a 0 следует: 2t 0,
2
2
2
t
t
t
или развернутое выражение
0
2
2
2
x y z
оператора Лапласа:
.
(2)
Для бесконечной пластины: h ;b , то есть:
2t / y2 0; 2t / z2 0 .
Дифференциальное уравнение
d 2t
0 .
теплопроводности запишется в виде:
(3)
2
dx

4. Условия однозначности

Для рассматриваемого случая добавляем
условия однозначности:
● Геометрические: вертикальная пластина h ;b ,
● Физические: Const;
● Начальные: для стационарного процесса не требуются,
● Граничные условия I рода: при x 0 t t Const;
Найти:
t f ( x) ?;q ?
при
c1
x t tc2 Const.
После первого интегрирования
дифференциального уравнения (3) имеем:
После разделения переменных в (5):
dt
c1;
dx
dt c1dx;
(4)
(5)
(6)

5. Температурное поле

t c1x c2.
После 2-го интегрирования:
Для определения констант интегрирования
подставляем (4) в (7):
при x 0 t
при
x
t tc2 c1 c2 c1 tc1;
откуда с учетом (5) имеем:
Откуда получаем:
t tC1
c1
tc 2 tc1
tC1 tC 2
x.
(7)
tc1 c2 ;
(8)
.
(9)

6. Удельный тепловой поток

По закону Фурье:
q
dt
,
dx
Подставляя (9) в (10), получим:
q (tc1 tc2 ),
или в форме закона Ома:
t
q .
R
(10)

7. Теплопроводность через трехслойную плоскую стенку

2
1
t
3
tc1
t'
q
t"
tc2
0
1
2
3
x

8. Теплопроводность через многослойную плоскую стенку при граничных условиях первого рода

Расчетная схема
λ
T c1
1
λ
λ
2
n
T c2
T
c3
T
cn
T
δ1
δ2
δn
cn+1

9. Удельный тепловой поток

Теплообмен в каждом слое опишется формулой:
tC 1 tC 2
,
q1 1
1
tC 2 tC 3
,
q2 2
2
tCn tCn 1
.
qn n
n
(1)

10. Удельный тепловой поток

Так как теплообмен стационарный, то: q1 q2 qn q (2)
Для вывода формулы перепишем уравнение (1) с учетом
уравнения (2), получим:
q 1
tC1 tC 2 ,
1
q 2
,
tC 2 tC 3
2
q n
tCn tCn 1 .
n

11. Удельный тепловой поток

Складываем части отдельно, получим:
tС1 tС 2 tС 2 tС 3
q 1
1
q 2
2
q n
n
tСт tСт 1
.

12. Удельный тепловой поток

Отсюда получим:
q
tC1 tCn 1
1 2
1 2
n
n

13. Теплообмен в плоской стенке при граничных условиях третьего рода.

Расчетная схема:
T ж1
T c1
α2
T c2
α1
T ж2
δ

14. Удельный тепловой поток

Теплообмен на правой и левой поверхности стенки опишется
законом Ньютона – Рихмана:
q1 1 t Ж1 tС1 ;
q2 2 tС 2 t Ж 2
Теплообмен внутри стенки:
q3
tС 2 tС 3

15. Удельный тепловой поток

q1 q2 q3 q
Разность температур:
t Ж 1 tС 1 ,
1
q
tC 2 t Ж 2
,
2
q
tC 1 tC 2
.
q

16. Удельный тепловой поток

Складываем:
t Ж 1 t С 1 t С 2 t Ж 2 tС 1 tС 2
q
q q
1 2

17. Удельный тепловой поток

Окончательно:
t Ж1 t Ж 2
q
1 1
1
2

18. Теплопроводность через многослойную плоскую стенку при граничных условиях третьего рода

Плотность теплового потока:
q
t Ж1 t Ж 2
i 1
1 i 1 i 2
1
n

19. Теплопроводность через однослойную плоскую стенку при граничных условиях второго рода

По закону Фурье:
dt
q
const
dx
Перепишем уравнение и проинтегрируем:
qdx dt ,
x
t
0
tC 1
q dx dt

20. Теплопроводность через однослойную плоскую стенку при граничных условиях второго рода

Получим:
qx t tC1 ,
выразим отсюда t:
t
1
tC1 qx
t tC1
qx

21. Графический метод определения температур между слоями

t
tc1
A
t'
C
B
t"
G
E
0
F
1
1
2
2
3
3
D
tc2
R

22. Определение температур между слоями

Треугольники АBC и ADE подобны между собой по равенству
трех углов. Из их подобия следует:
AC AE
tg
,
BC DE
то есть
или:
tg
tc1 t '
1
1
tc1 tc2
1 2 3
1 2 3
q,
AC tc1 t ' , откуда находится температура t ' .
Аналогично, из подобия треугольников AFG и ADE:
AG tc1 t".
Отсюда находится температура
t".

23. Теплопроводность через однослойную цилиндрическую стенку

Const
t
tc1
r
r1
r2
0
q
dr
tc2
r

24. Дифференциальное уравнение тепло-проводности для цилиндрической стенки

Дифференциальное уравнение теплопроводности для цилиндрической стенки
Общее выражение дифференциального уравнения
qv
теплопроводности: t
2
a t
c
.
(1)
Для стационарного процесса
t / 0;
при отсутствии внутренних источников теплоты qv 0,
с учетом этих условий уравнение (1) примет вид a 2t 0 .
Но a 0 , тогда частный вид дифференциального уравнения
теплопроводности: 2t 0.
Или через развернутое выражение оператора Лапласа:
2
2
2
t
1
t
1
t
t
2 2 2 0 .
2t 2
r r r r z
(2)

25. Условия однозначности

Добавляем условия однозначности:
● Геометрические условия:
r2 (бесконечная цилиндрическая стенка);
● Физические условия: Const;
● Начальные условия: для стационарного процесса не
требуются;
● Граничные условия I рода:
при
при
r r1
t tc1 Const;
r r2
t tc2 Const.
(3)

26. Преобразование дифференциального уравнения

В соответствии с геометрическими условиями однозначности,
в бесконечной цилиндрической стенке температура не изменяется по координатам z и , тогда уравнение (2) примет вид:
(4).
Найти: t f (r ) ?;Q ?.
2
d t 1 dt
0,
2
dr r dr
Граничные условия:
Обозначим
dt
U ,
dr
t r1 tC1 ,
t r2 tC 2 .

27. Преобразование дифференциального уравнения. Решение

Уравнение (4) примет вид:
Проинтегрируем:
Получим:
dU 1
U 0
dr r
dU
dr
U r ,
ln U ln r ln C1

28. Решение

Найдем из полученного выражения
ln(Ur ) ln C1;
dt
r C1 ,
dr
t C1 ln r C2
Ur C1
dr
dt C1 r ,

29. Решение

Решение подчиним граничным условиям:
tС1 С1 ln r1 C2 ,
,
tC 2 C1 ln r2 C2 .
tС1 tС 2 С1 ln r1 C 2 C1 ln r2 C2
tС 1 t С 2
r1
C1 ln
r2

30. Решение

Отсюда следует:
C1
tC 1 t c 2
r1
ln
r2
Решение примет вид:
tC 1 t C 2
C 2 tC 1
ln r1.
r1
ln
r2
r
tС1 tС 2 ln
r1
t tС 1
,
r2
ln
r1

31. Тепловой поток

По закону Фурье:
Q
tC1 tC 2 2 l
Q
r2
ln
r1
Q
ql ,
l
Вт
м
где
dt
F , Вт
dr
или
Q
F 2 rl
tC1 tC 2 l
ql
r2
1
ln
2 r1
,
tC1 tC 2
d2
1
ln
2 d1

32. Теплообмен в цилиндрической стенке при граничных условиях второго рода

По закону Фурье:
dt
Q 2 rl const
dr
Проинтегрируем данное выражение:
получим:
r
t
dr
Q 2 l dt
r
r1
tC 1
r
Q ln 2 l t tC1
r1
Q
r
t tC1
ln
2 l r1

33. Теплообмен при граничных условиях третьего рода

T
Теплообмен на внутренней
и наружной поверхности
стенки описывается законом
Ньютона – Рихмана:
ql1 1 t Ж1 tС1 d1
ql 2 2 tС 2 t Ж 2 d2
Внутри стенки:
ql 3
tC1 tC 2
d2
1
ln
2 d1
Расчетная схема:
T ж1
α2
Т с1
α1
Т с2
d1
Т ж2
d2
d
.

34. Теплообмен при граничных условиях третьего рода

Так как теплообмен стационарный, то
ql
tC 2 t Ж 2
,
d 2 2
d2
1
tC1 tC 2 ql
ln .
2 d1
ql
t Ж 1 tС 1
,
d1 1
ql1 ql 2 ql 3 ql

35. Теплообмен при граничных условиях третьего рода

Получим:
t Ж 1 tС1 tС 2 t Ж 2 tС1 tС 2
1
d2
1
1
ql
ln
d1 1 d 2 2 2 d1
Уравнение теплопередачи через цилиндрическую стенку:
ql
t Ж1 t Ж 2
1
d2
1
1
ln
1d1 2 d1 2 d 2

36. Теплообмен при граничных условиях третьего рода

Линейное термическое сопротивление теплопередачи через
цилиндрическую стенку:
d2
1
1
1 мК
Rl
ln
,
1d1 2 d1 2 d 2 Вт
Тогда уравнение теплопередачи:
ql
t Ж1 t Ж 2
Rl

37. Теплообмен при граничных условиях третьего рода

Полный тепловой поток:
Q
t Ж1 t Ж 2 l
d2
1
1
1
ln
1d1 2 d1 2 d 2
Q ql l
, Вт

38. Теплообмен при граничных условиях третьего рода

Линейный коэффициент теплопередачи через цилиндрическую
стенку:
1 Вт
kl
,
Rl м К
Тогда уравнение теплопередачи:
ql kl t Ж1 t Ж 2

39. Плотность теплового потока

Q Вт
q , 2 ;
F м
F1 d1l;
F2 d 2l.
t Ж1 t Ж 2
,
На внутренней поверхности: q1
d1
1 d1 d 2
ln
1 2 d1 2 d 2
На внешней поверхности:
t Ж1 t Ж 2
q2
.
d2
d2 d2 1
ln
1d1 2 d1 2

40. Теплопроводность через трехслойную цилиндрическую стенку

2
1
t
3
tc1
t'
r1
r2
r3
r4
0
q
t"
tc2
r

41. Теплопроводность через многослойную цилиндрическую стенку

Уравнение теплопередачи:
ql
t Ж1 t Ж 2
n
1
1
1 di 1
1
ln
1d1 2 i 1 i
di 2 d 2
, Вт / м

42. Критический диаметр цилиндрической стенки

Линейное термическое сопротивление теплопередачи через
цилиндрическую стенку:
d2
1
1
1 мК
Rl
ln
,
1d1 2 d1 2 d 2 Вт
Исследуем функцию вида:
Rl Rl (d 2 ).
Функция непрерывна и дифференцируема.
dRl
1
1
0.
2
d (d 2 ) 2 d 2 2 d 2

43. Критический диаметр цилиндрической стенки

Найдем критическую точку.
Критическая точка:
d 2 Rl
d d 2
2
1 1
1
2
0 d2
d2 2 2 d2
2
2
d2
2
1
2
1 2
1
2 d 22 2 d 23 d 22 2 d 2 2
2 2
2
1
1 1 1 1
1
0
2 d2 2 2 2 2 2 2

44. Критический диаметр тепловой изоляции

Теплоизоляционными называются материалы,
теплопроводность которых не превышает величины
0,25 Вт/(мК).
● Естественная изоляция (природная): асбест, слюда, пробка.
● Предварительно обработанная: асбослюда, шлаковата,
стекловата, пенопласт, пеношлакобетон.
Теплоизоляционные свойства последним из перечисленных
материалов придает наличие в них мелких воздушных пузырьков или прослоек воздуха. В них из-за малости размеров,
конвекция отсутствует и теплота передается только теплопропроводностью, порядок которой для воздуха при атмосферных
условиях порядка 0,025 Вт/(мК), то есть на порядок ниже
величины, приведенной выше для теплоизоляции.

45. Термическое сопротивление теплопере- дачи через изолированный трубопровод

Термическое сопротивление теплопередачи через изолированный трубопровод
Линейное термическое сопротивление теплопередачи
через двухслойную цилиндрическую стенку:
d
1
1 d2
1
1
(1)
R
n
n из
.
1d1 2 d1 2 из d 2 2 dиз
В выражении (1):
при: dиз var
R1
R 2 R3
1
1 d2
n Const;
1d1 2 d1
1
2 из
n
(2)
dиз
1
var. (3)
d 2 2 dиз
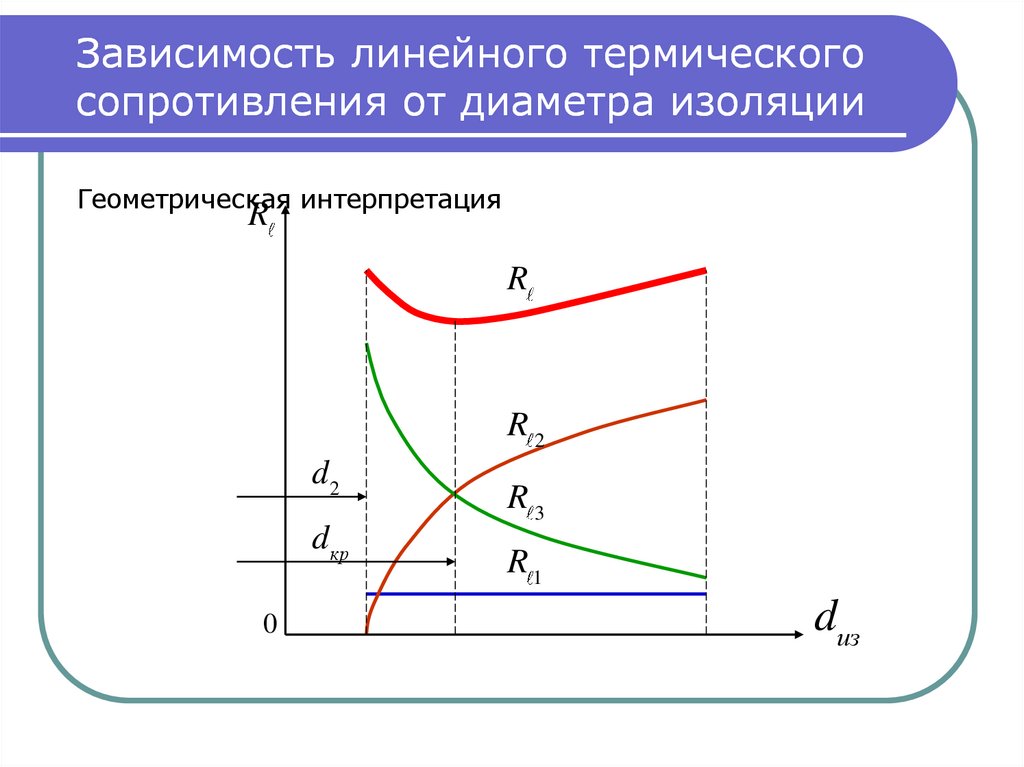
Из (3) видно, что с увеличением диаметра изоляции d
из
R
термическое сопротивление R растет, а
3 падает.
2

46. Зависимость линейного термического сопротивления от диаметра изоляции

Геометрическая интерпретация
R
R
R2
d2
dкр
0
R3
R1
dиз

47. .

Исследование функции (3)
на минимум
.
Из предыдущих двух слайдов следует, что минимальному
термическому сопротивление при d
соответствуют
кр
максимальные теплопотери.
Для определения критического диаметра изоляции надо
исследовать функцию (3) на минимум, а именно:
.
d
d
1
1
[
n( из )
] 0
,
d (dиз ) 2 из
d 2 2 dиз
или в виде
d
1
1
[
( ndиз nd2 )
] 0.
d (dиз ) 2 из
2 dиз
Тогда при
из Const;d2 Const; 2 Const,
и с учетом
1 1
x x
( nx)' ;( )'
1
;( nd2 )' 0,
2
x
имеем:

48. .

Выбор эффективной изоляции
трубопроводов
.
1
1
1
0.
2
2 из d кр 2 d кр
.
После сокращения на
или
2dкр 2 из 0,
:
dкр
1
2 из
1
0,
2 d кр
откуда критический диаметр изоляции:
dкр
2 из
2
.
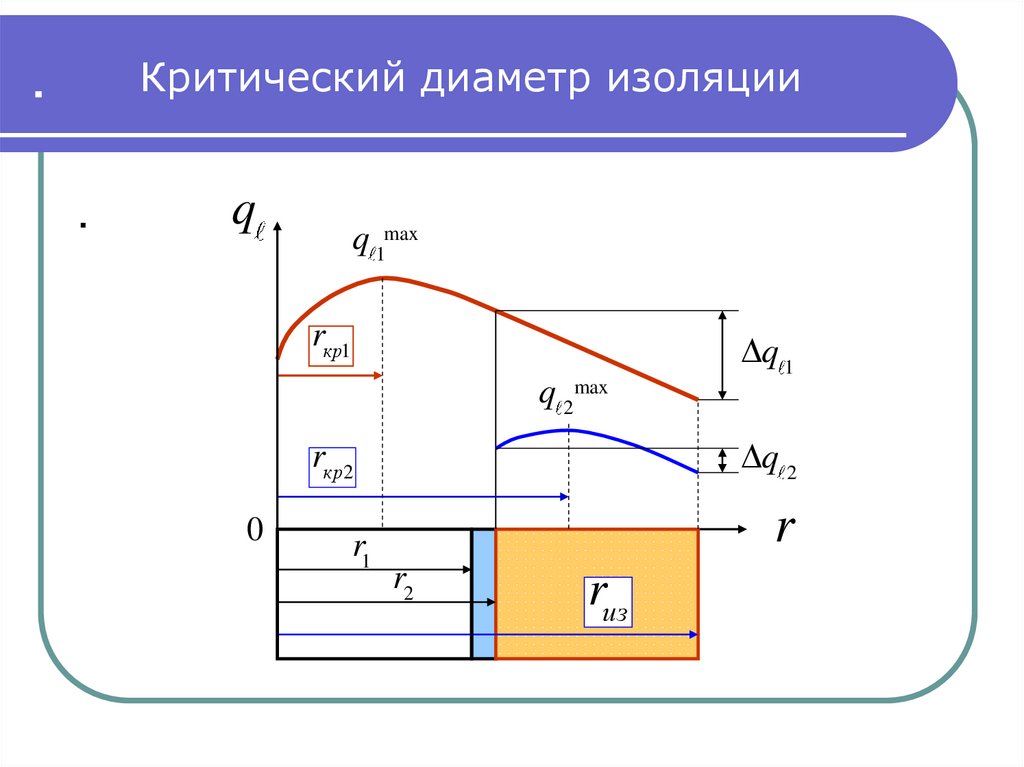
Из следующего слайда видно, что при
эффективная
а при
dкр d2
q 2 q 1
,
- малоэффективная.
dкр d2
- изоляция

49. .

Критический диаметр изоляции
.
.
q
q 1max
rкр1
q 1
q 2max
q 2
rкр2
0
r1
r
r2
rиз