Тепломассообмен. Теплопроводность при стационарном тепловом режиме (часть 1)

1. ТЕПЛОМАССООБМЕН

Теплопроводность при
стационарном тепловом
режиме (часть 1)
Лекция № 3
2016 год

2. План

• 1. Передача теплоты через однослойную плоскую стенку
при граничных условиях I–го рода.
• 2. Передача теплоты через многослойную плоскую стенку
при граничных условиях I–го рода.
• 3. Передача теплоты через однослойную цилиндрическую
стенку при граничных условиях I–го рода.
• 4.
Передача
теплоты
через
многослойную
цилиндрическую стенку при граничных условиях I–го
рода.
• 5. Передача теплоты через шаровую стенку при
граничных условиях I–го рода.
• 6. Теплопроводность тел с внутренними источниками
теплоты.

3. 1. Передача теплоты через однослойную плоскую стенку при граничных условиях I–го рода

Дифференциальное уравнение теплопроводности позволяет
определить температуру в зависимости от времени и координат
в любой точке поля.
Для любого случая к нему надо присоединить необходимые
краевые условия.

4. Теплопроводность через однослойную плоскую стенку (самый распространенный случай)

Длина и ширина плоской стенки бесконечно велики по сравнению с
ее толщиной δ.
Стенка имеет постоянную толщину δ.
Температуры поверхностей стенки t1 и t2 поддерживаются
постоянными, т.е. они являются изотермическими поверхностями.
Температура меняется только направлении перпендикулярном
плоскости стенки, которое принимаем за ось x.
Теплопроводность λ постоянна для всей стенки.

5.

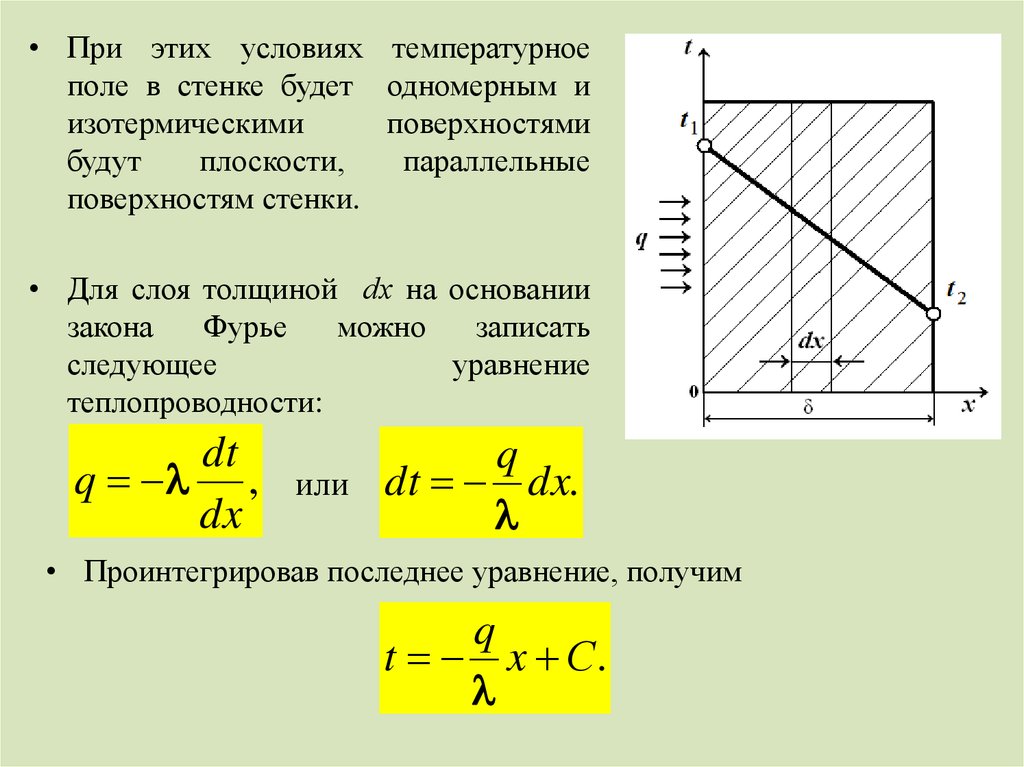
• При этих условиях температурное
поле в стенке будет одномерным и
изотермическими
поверхностями
будут
плоскости,
параллельные
поверхностям стенки.
• Для слоя толщиной dх на основании
закона
Фурье
можно
записать
следующее
уравнение
теплопроводности:
dt
q ,
dx
или
q
dt dx.
• Проинтегрировав последнее уравнение, получим
q
t x С.

6.

q
t x С.
Из этого уравнения следует, что
температура изменяется по толщине
стенки по линейному закону.
Константа
интегрирования
С
определяется из условий на границах
стенки:
если х = 0, то t = t1, откуда С = t1.
Если х = δ, то t = t2 и данное уравнение
принимает вид
q
t2 t1.
Из
этого
определяем
мощности
потока q:
уравнения
значение
теплового
q t1 t2 t.

7.

Константа интегрирования С
определяется из условий на
границах стенки:
если х = 0, то t = t1, откуда С = t1.
Если х = δ, то t = t2 и данное
уравнение принимает вид
q
t2 t1.
Значение
мощности
теплового
потока q определим из уравнения:
q t1 t2 t.

8.

• Общее количество теплоты QT, которое передается
через поверхность стенки F за время τ:
QT F t1 t 2 ,
• где
– тепловая проводимость стенки.

9.

• Тепловой поток Q зависит не от абсолютного
значения температур, от разности температур на
наружных поверхностях стенки:
Q qF F t1 t 2 F t ,
где
t t1 t 2 называется температурным
напором.

10. Распределение температур при постоянном и переменном коэффициентах теплопроводности

• Уравнение q t1 t 2 t
• справедливо для случая, когда теплопроводность является
постоянной величиной.
• Теплопроводность реальных тел зависит от температуры и
закон изменения температур выражается кривой линией.
• Если теплопроводность зависит от температуры в
незначительной степени, то на практике закон изменения
температур считают линейным.

11.

• В уравнение q t1 t 2 t
• Введем поправки на зависимость λ от t, считая эту
зависимость линейной:
0 1 bt .
• Подставим эту зависимость в уравнение Фурье, получаем
dt
dt
q t 0 1 bt .
dx
dx
• Разделив переменные и интегрируя, получаем
bt 2
C.
qx 0 t
2

12.

• При граничных значениях переменных имеем:
bt12
C.
при x=0, t=t1 и 0 0 t1
2
2
bt 2
при x=δ, t=t2 и q 0 t 2
C.
2
• Вычитая из второго равенства первое, находим
0
q
t1 t 2
1 b 2 t1 t 2 .
• Полученное уравнение позволяет определить поверхностную
плотность
теплового
потока
при
переменной
теплопроводности.

13.

Множитель 0 1 b t1 t 2 2 является среднеинтегральным
значением теплопроводности.
• В уравнении q t1 t 2
• теплопроводность λ была принята постоянной и равной
среднеинтегральному значению теплопроводности λср.
ср 0 1 b t1 t 2 2
• Плотность (мощность) теплового потока можем определить
по формуле
q
ср
t1 t 2 .

14.

• Уравнение температурной кривой в стенке получается путем
решения квадратного уравнения
2
bt
C
qx 0 t
2
относительно t и подстановки значения С из уравнения
2
bt1
C.
0 0 t1
2
2
2qx 1
1
t x t1
.
b
0b b
Из данного уравнения следует, что температура внутри стенки
изменяется по кривой. Если коэффициент b отрицателен, то
кривая направлена выпуклостью вниз; если b положителен, то
выпуклостью вверх.

15. 2. Передача теплоты через многослойную плоскую стенку при граничных условиях I–го рода

В тепловых аппаратах часто встречаются стенки, состоящие из
нескольких плоских слоев различных материалов.
Выведем уравнение для этого случая.
Будем полагать, что все слои плотно прилегают друг к другу.

16.

• Выведем расчетную формулу теплопроводности
сложной стенки при стационарном состоянии из
уравнения теплопроводности для отдельных слоев.
• Тепловой поток, проходящий через любую
изотермическую поверхность неоднородной стенки,
один и тот же.

17.

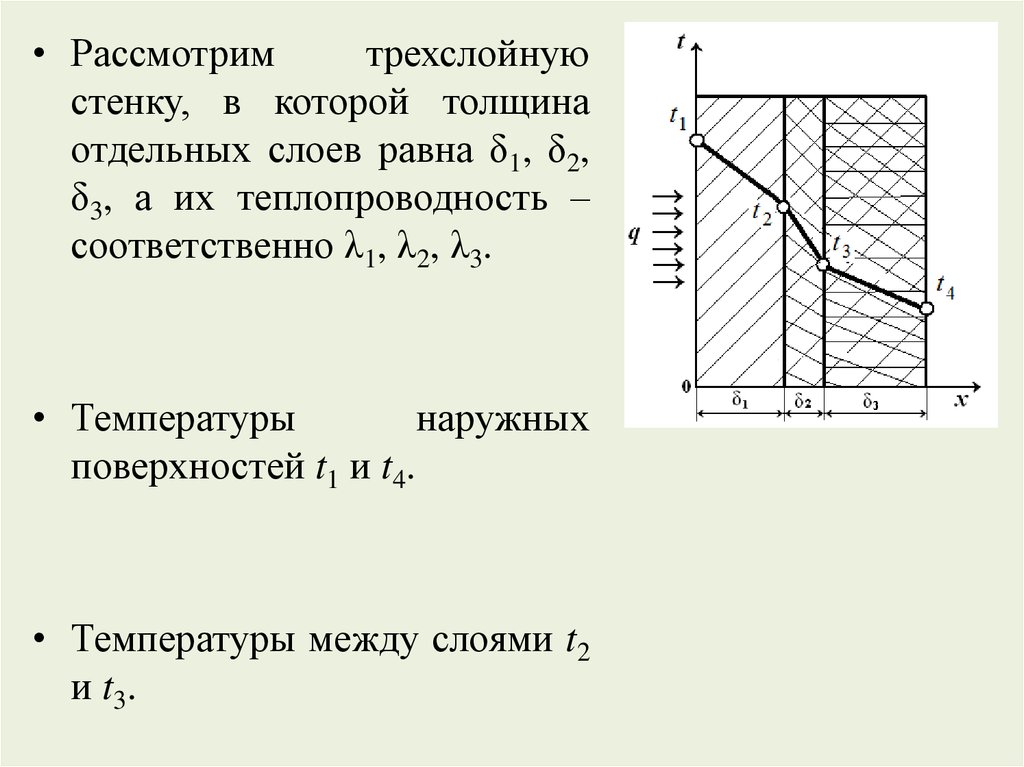
• Рассмотрим
трехслойную
стенку, в которой толщина
отдельных слоев равна δ1, δ2,
δ3, а их теплопроводность –
соответственно λ1, λ2, λ3.
• Температуры
наружных
поверхностей t1 и t4.
• Температуры между слоями t2
и t 3.

18.

• Тепловой поток для каждого слоя:
1
Q F t1 t2 ,
1
2
Q
F t2 t3 ,
2
3
Q F t3 t4 ,
3
Выразим
температур
слоя:
разности
для каждого
Q 1
t1 t2
,
F 1
Q 2
t2 t3
,
F 2
Q 3
t3 t4
,
F 3

19.

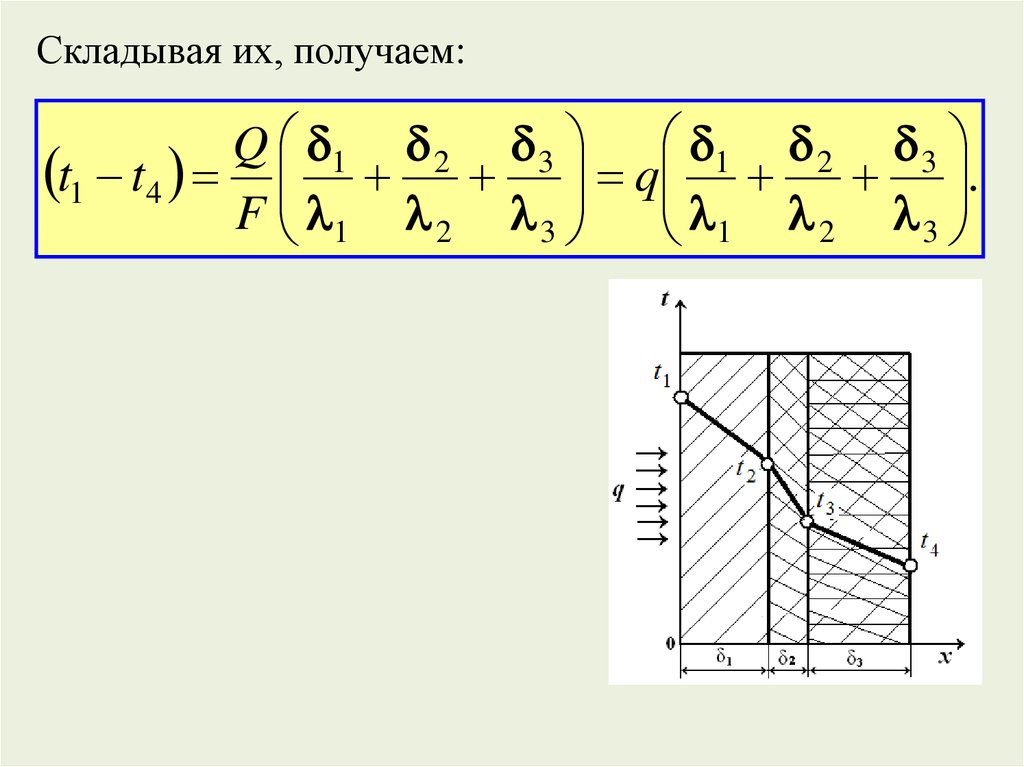
Складывая их, получаем:
1 2 3
Q 1 2 3
t1 t4 q .
F 1 2 3
1 2 3

20.

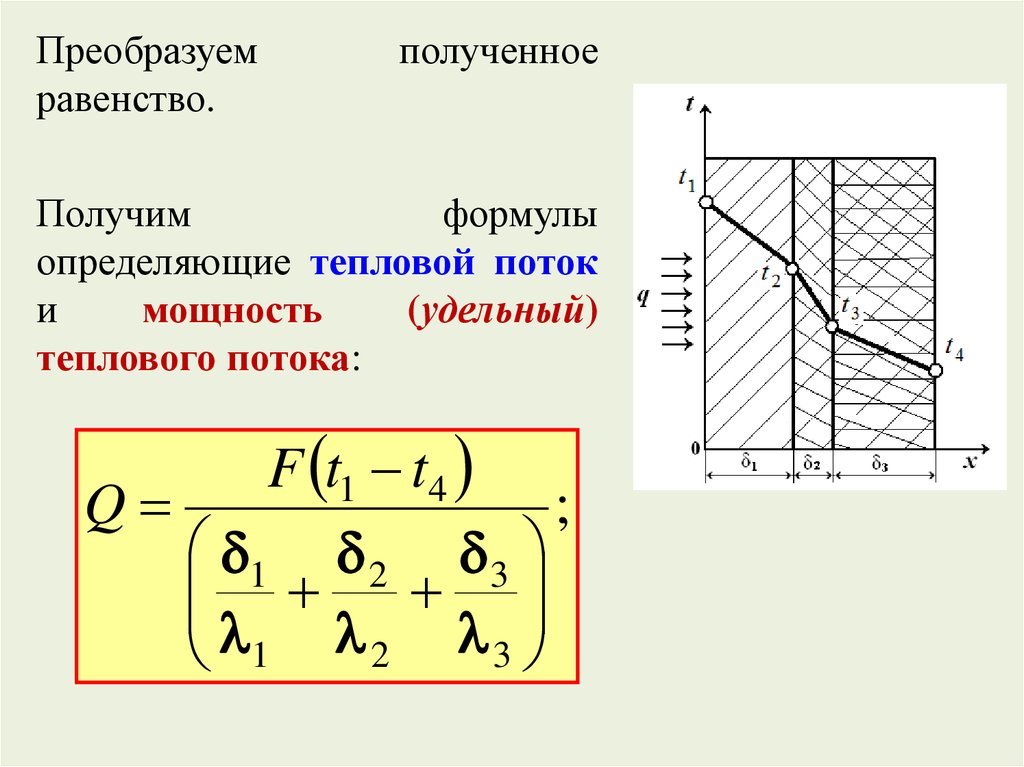
Преобразуем
равенство.
полученное
Получим
формулы
определяющие тепловой поток
и
мощность
(удельный)
теплового потока:
F t1 t4
Q
;
1 2 3
1 2 3

21.

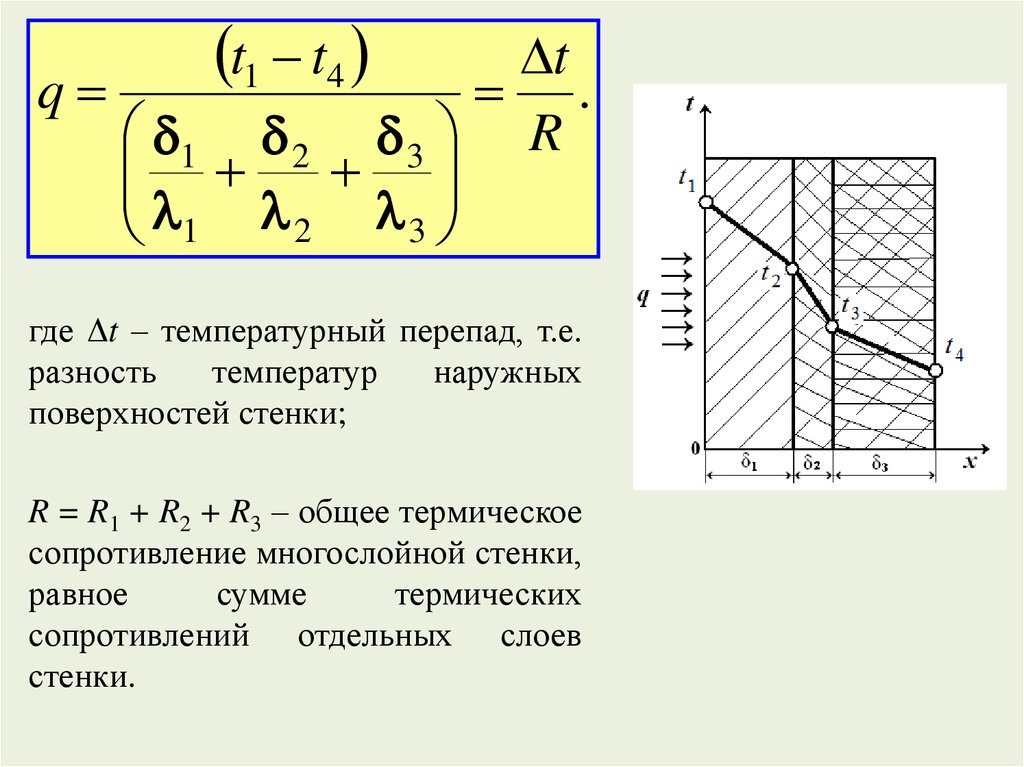
t1 t4
t
q
.
1 2 3 R
1 2 3
где Δt – температурный перепад, т.е.
разность
температур
наружных
поверхностей стенки;
R = R1 + R2 + R3 – общее термическое
сопротивление многослойной стенки,
равное
сумме
термических
сопротивлений отдельных слоев
стенки.

22.

R
– термическое сопротивление слоя;
i – полное термическое
сопротивление
R
многослойной плоской стенки.
i 1 i
i n

23.

Температуры (°С) между отдельными слоями сложной стенки
находим из следующих уравнений:
Q 1
t2 t1 ;
F 1
Q 2
t3 t2 ;
F 2
Q 3
t4 t3 .
F 3
• Температура в каждом слое стенки при постоянной
теплопроводности изменяется по линейному закону, а для
многослойной стенки температурный график представляет
собой ломаную линию.

24. 3. Передача теплоты через однослойную цилиндрическую стенку при граничных условиях I–го рода

25.

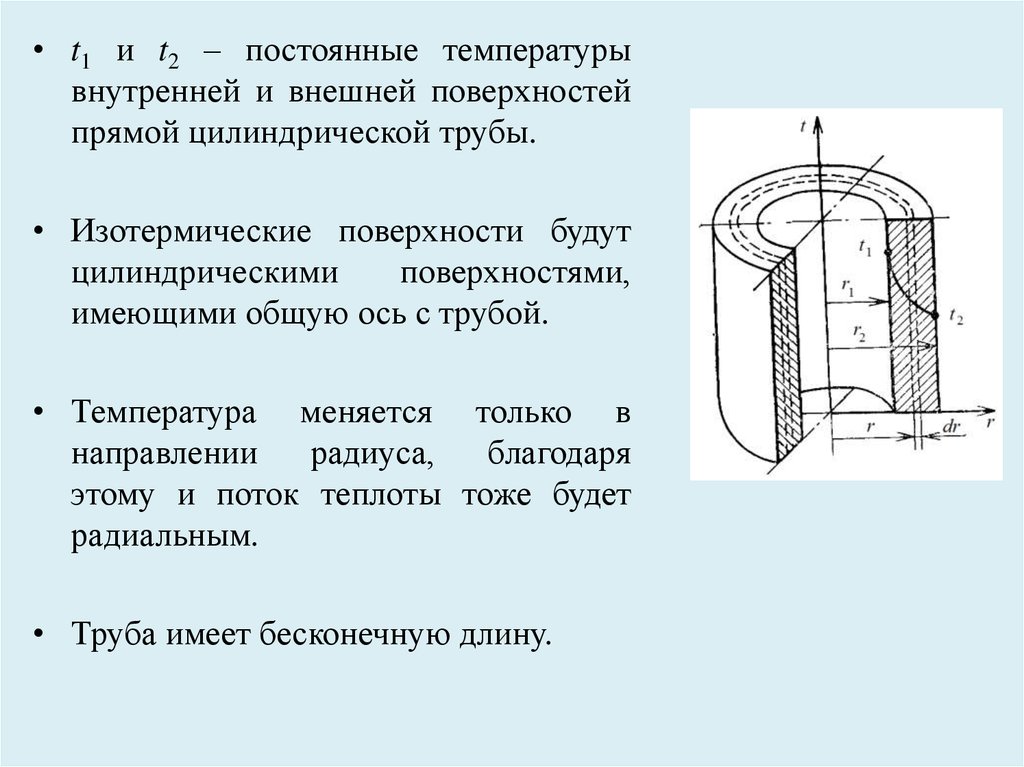
• t1 и t2 – постоянные температуры
внутренней и внешней поверхностей
прямой цилиндрической трубы.
• Изотермические поверхности будут
цилиндрическими
поверхностями,
имеющими общую ось с трубой.
• Температура меняется только в
направлении
радиуса,
благодаря
этому и поток теплоты тоже будет
радиальным.
• Труба имеет бесконечную длину.

26.

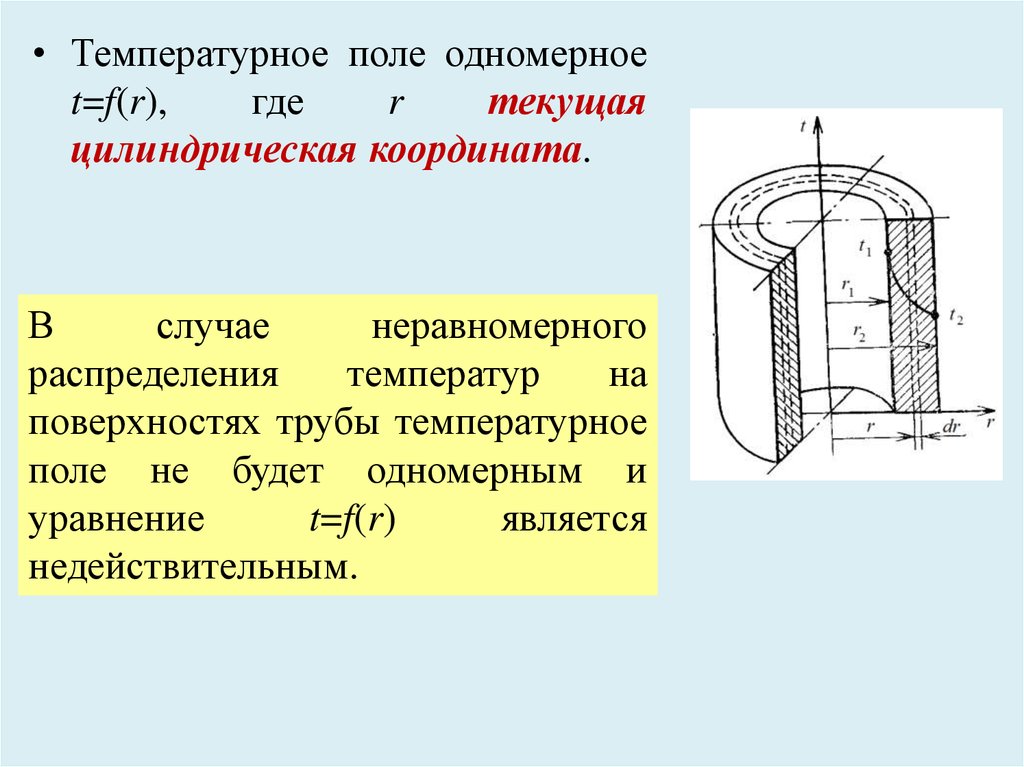
• Температурное поле одномерное
t=f(r),
где
r
текущая
цилиндрическая координата.
В
случае
неравномерного
распределения
температур
на
поверхностях трубы температурное
поле не будет одномерным и
уравнение
t=f(r)
является
недействительным.

27.

• Рассмотрим участок трубы
длинной l, в которой тепловой
поток направлен радиально.
• Поверхность F на расстоянии r
от оси равна 2πrl.
• t1 и t2 – температуры внутренней
и внешней поверхностей трубы.

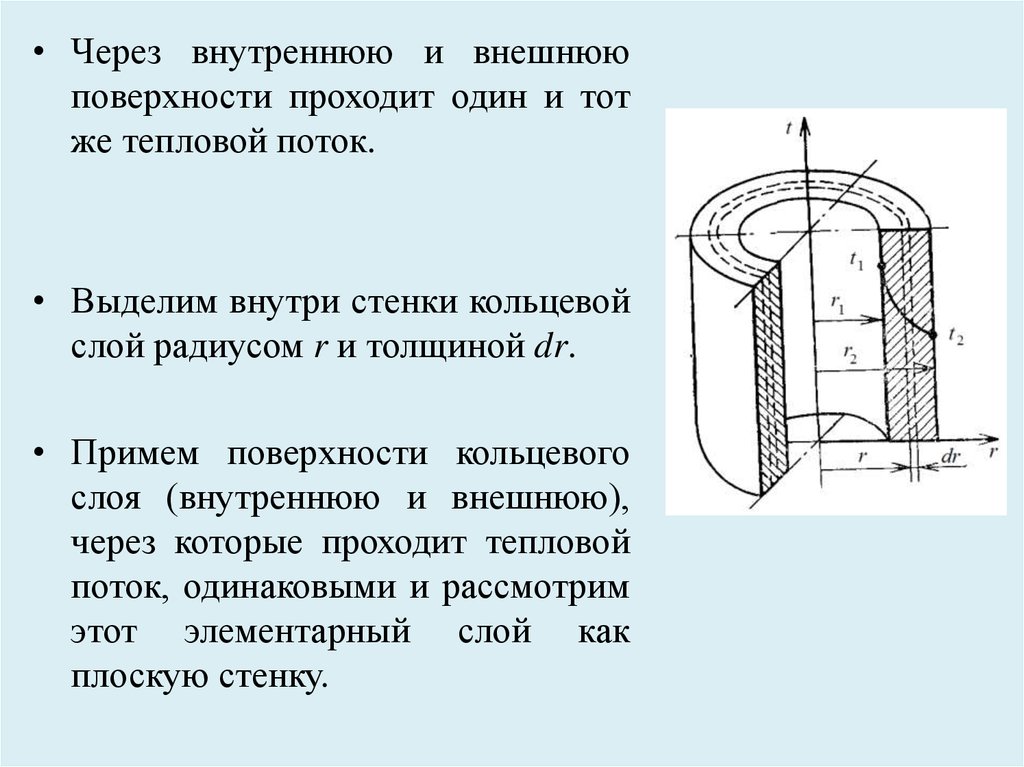
28.

• Через внутреннюю и внешнюю
поверхности проходит один и тот
же тепловой поток.
• Выделим внутри стенки кольцевой
слой радиусом r и толщиной dr.
• Примем поверхности кольцевого
слоя (внутреннюю и внешнюю),
через которые проходит тепловой
поток, одинаковыми и рассмотрим
этот элементарный слой как
плоскую стенку.

29.

• Разность
температур
между
поверхностями элементарного слоя
будет бесконечно малой dt.
• По закону Фурье,
dt
Q F ,
dr
• для кольцевого слоя
dt
Q 2 lr .
dr

30.

• Разделяя переменные, получаем
Q dr
dt
.
2 l r
• Интегрируя полученное уравнение в пределах от t1
до t2 и от r1 до r2 и при λ=const, получаем
r2
Q
t1 t2
ln .
r1
2 l

31.

• Выразим тепловой поток
l t1 t 2
Q
.
d2
1
ln
d1
2
• Выводы из полученного уравнения:
• Распределение температур в стенке цилиндрической
трубы представляет собой логарифмическую кривую.
• Тепловой поток, проходящий через цилиндрическую
стенку, определяется заданными граничными условиями
и зависит от отношения наружного диаметра к
внутреннему.

32.

• Тепловой поток может быть отнесен к единице длины трубы
ql и к 1 м2 внутренней или внешней поверхности q1 и q2.
Расчетные формулы принимают следующий вид:
Q 2 t1 t 2
ql
;
d2
l
ln
d1
2 t1 t 2
Q
q1
;
d2
d1l
d1 ln
d1
2 t1 t 2
Q
q2
.
d2
d 2 l
d 2 ln
d1

33. 4. Передача теплоты через многослойную цилиндрическую стенку при граничных условиях I–го рода

34.

• Цилиндрическая стенка состоит
из трех плотно прилегающих
слоев.
• Температура
внутренней
поверхности стенки t1, наружной
t4.
• Температуры между слоями t2 и
t3.

35.

• Теплопроводность слоев равны
λ1, λ2, λ3.
• Диаметры слоев равны d1, d2, d3,
d 4.
• Температура каждого слоя стенки
изменяется по логарифмической
кривой.
• Общая температурная кривая
представляет собой ломаную
логарифмическую кривую.

36.

• При стационарном режиме через все слои проходит
один и тот же тепловой поток.
• Для каждого слоя тепловой поток равен:
2 1l t1 t2
Q
;
ln d 2 d1
2 2l t2 t3
Q
;
ln d3 d 2
2 3l t3 t4
Q
.
ln d 4 d3

37.

• Решая
полученные
разности температур
получаем
уравнения
относительно
и почленно складывая,
Q 1 d 2 1 d3 1 d 4
t1 t4 ln ln ln ,
2 l 1 d1 2 d 2 3 d3
• откуда
2 l t1 t4
Q
.
1 d 2 1 d3 1 d 4
ln ln ln
1 d1 2 d 2 3 d3

38.

Температуры (°С) между слоями находим из следующих
уравнений:
Q d2
t2 t1
ln ;
2 1l d1
Q d3
t3 t2
ln .
2 2l d 2

39. 5. Передача теплоты через шаровую стенку при граничных условиях I–го рода

40.

• Постоянный тепловой поток направлен через шаровую стенку.
• Источник теплоты находится внутри шара.
• Температура изменяется только по направлению радиуса.
• Изотермические
поверхности
представляют
концентрические шаровые поверхности.
собой
• Температура внутренней поверхности стенки t1, наружной t2.
• Теплопроводность стенки λ постоянна.
• Внутренний радиус шара r1, наружный r2.

41.

• Тепловой поток, проходящий через шаровой слой
радиусом r и толщиной dr, находим из уравнения
Фурье:
dt
2 dt
Q F 4 r ,
dr
dr
• или
Q dr
dt
2 .
4 r

42.

Q dr
dt
2 .
4 r
• Интегрируя данное уравнение по t и r.
• Постоянную
интегрирования
определяем
граничных условий
при r = r1, то t = t1,
при r = r2, то t = t2, получаем
4 t1 t2 2 t1 t2
Q
.
1 r1 1 r2 1 d1 1 d2
из