Теплопроводность при наличии внутренних источников теплоты

1. Проблемы энерго- и ресурсосбережения в теплоэнергетике

Теплопроводность при наличии
внутренних источников теплоты

2. Теплопроводность при наличии внутренних источников теплоты

Примеры:
• джоулева теплота при пропускании электрического
тока;
• экзо- и эндотермические химические реакции;
• выделение (поглощение) теплоты при перестройке
кристаллических решеток;
• выделение (поглощение) теплоты при изменении
агрегатного состояния тела;
• выделение (поглощение) теплоты в атомных
реакторах….

3. Теплопроводность при наличии внутренних источников теплоты

Классификация источников теплоты
По форме:
• Точечные;
• Линейные;
• Поверхностные;
• Объемные.
По направлению действия:
• Положительные (теплота выделяется);
• Отрицательные (теплота поглощается).

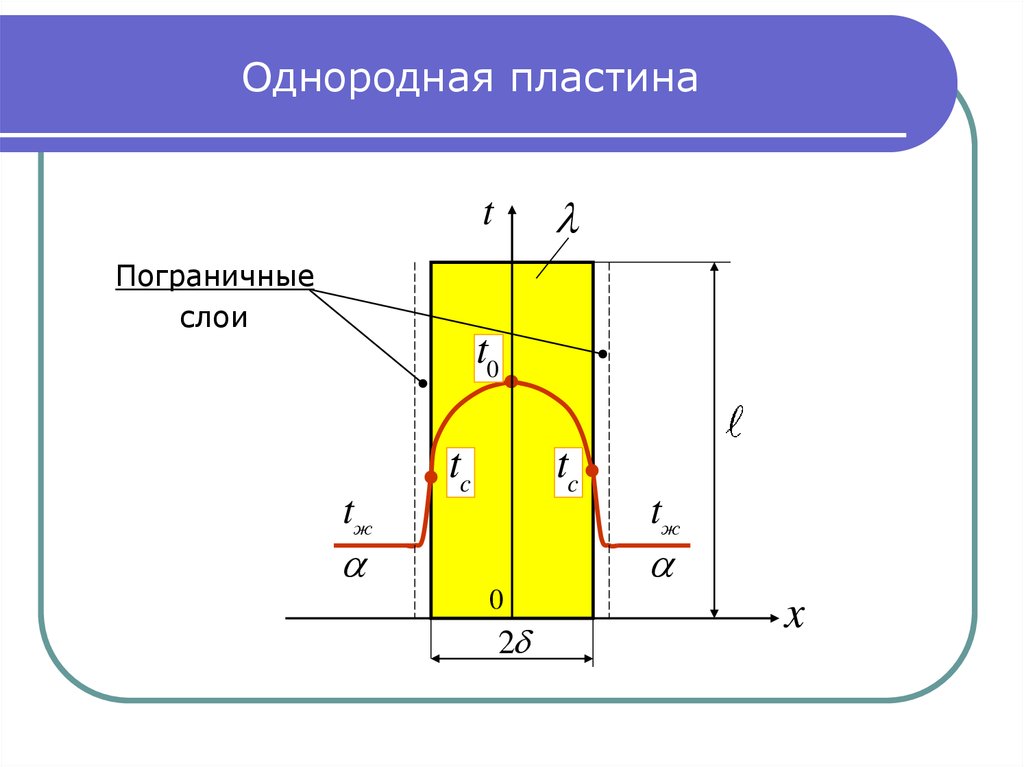
4. Однородная пластина

t
Пограничные
слои
t0
tж
tc
tc
0
2
tж
x

5. Дифференциальное уравнение теплопроводности

: бесконечная пластина.
В стационарном процессе: q Const; Const;t Const.
v
ж
Найти: t f ( x) ?;t ?;t ?
0
c
q
t
Дифференциальное
a 2t v .
уравнение теплопроводности:
(1)
c
При
Для стационарного процесса:
тогда
a 2t
qv
0,
c
(2) где
( t / ) 0 ,
2
2
2
t
t
t
2t 2 2 2
x y z
оператор Лапласа, тогда после деления (2) на
a /(c )
дифференциальное уравнение теплопроводности
в бесконечной пластине:
2t 2t
2 2 0,
y z

6. Дифференциальное уравнение теплопроводности

Дифференциальное уравнение примет вид:
2
d t qv
0
2
dx
(3)

7. Граничные условия

Условия теплоотдачи одинаковы с обеих сторон пластины,
поэтому температурное поле симметричное, а тепловыделения
в обеих половинах пластины одинаковы, то есть можно рассматривать только ее правую
половину. Тогда граничные условия будут:
dt
x 0 ( ) x 0 0;
dx
dt
x ( ) x (tc tж ).
dx
(4)

8. Решение

Интегрируем (3):
qv
dt
x c1,
dx
разделяем переменные:
dt
qv
xdx c1dx.
(5)

9. Решение

После второго интегрирования:
qv 2
t x c1x c2
2
.
(6)

10. Константы интегрирования

Константы интегрирования находятся из граничных
условий (4) и уравнения (5) при:
x 0 c1 ( dt )x 0 0
dx
, (7)
x ( dt )x q.v
dx
q
dt
) x v (tc tж ).
dx
tc tж qv .
После сокращения на λ имеем:
Подставляем (10) в (6) при x и с учетом, что c 0:
1
2
q
получаем:
.
t tc v c2.
2
Приравнивая (10) и (11),
2
qv 2
имеем: qv
, откуда: c t qv qv .
tж
c2 ,
2
ж
2
2
Подставляем (8) в (4):
(
(8)
(9)
(10)
(11)
(12)

11. Частное решение

Подставим константы интегрирования (7) и
(12) в (6):
qv
qv 2 2
t tж
( x )
2
(13)

12. Тепловой поток

По закону Фурье:
dt
q
dx
Тепловой поток, отдаваемый от правой половины
пластины:
q qv , Вт /
2
м
Q qvV /2 qv f qf ,
(14)

13. Температуры

Если температура стенки известна или
вычислена по уравнению (10), то есть
заданы граничные условия I рода:
qv 2 2
t tc ( x ),
2
тогда при
x 0:
(15)
qv 2
q
t t0 tc tc
2
2

14. Однородный цилиндр

t
Пограничные
слои
t0
tc
tc
tж
tж
0
2r0
r

15. Дифференциальное уравнение теплопроводности для цилиндра

2r0 .
При стационарном режиме qv Const; Const;tж Const.
Для бесконечного цилиндрического стержня
Найти
t f (r);t0;tc
qv
t
2
a t .
c
Для стационарного процесса:
тогда:
a 2t
qv
0,
c
t
0,
(2)

16. Дифференциальное уравнение теплопроводности для цилиндра

Оператор Лапласа в полярных (цилиндрических)
координатах:
2t
t 1 t 1 t t
.
2
2
2
2
r r r r z
2
2
2
(3)
В бесконечном цилиндре температура изменяется
только по по радиусу, то есть:
t t
0,
2
2
z
2
2

17. Дифференциальное уравнение теплопроводности для цилиндра

После деления на:
a
c
получим дифференциальное уравнение
теплопроводности для цилиндра при
стационарном режиме:
2
d t 1 dt qv
0
2
dr r dr
(4)

18. Дифференциальное уравнение теплопроводности для цилиндра

Граничные условия:
dt
r 0 ( )r 0 0;
dr
dt
r r0 ( )r r (tc tж ).
dr 0
(5)

19. Решение

t f (r);t0;tc
Найти:
dt
U
dr
qv
dU 1
U
0
dr r
rdU Udr
qv
rdr 0

20. Решение

Обозначим:
V Ur dV rdU UdV
тогда
2
qv r
V
2
qv
dV rdr 0
2
qv r
dt
r
C1
dr
2

21. Общее решение

.
qv
dr
dt
rdr
C
1
2
r
2
qv r
t
C1 ln r C2
4

22. Частное решение

Подчиним граничным условиям:
qv 2r
4
qv 2r
4
1
C1
0
r r 0
r 0
qv r
C2
C2 tж
4
2
r r0

23. Частное решение

Тогда:
qv r0
q r
C2 tж
2
4
2
qv r0 qv r0
C2
tж
2
4
2
v 0

24. Частное решение

Тогда:
2
v 0
qv 2 qv r0 q r
t
r
tж
4
2
4

25. Частное решение

Температура на оси цилиндра :
qv r0 1 r0
t (0) tж
2 2
Температура на поверхности цилиндра :
qv r0
t (r0 ) tж
2

26. Тепловой поток

По закону Фурье:
dt
q
dr
qv 2r qv r
q(r )
4
2
qv r0
q(r0 )
2

27. Тепловой поток

Полный тепловой поток:
qv r0
Q qF
2 r0
2
2
qv r0

28. Цилиндрическая стенка

Дифференциальное уравнение теплопроводности для
цилиндра при стационарном режиме:
2
d t 1 dt qv
0
2
dr r dr
Общее решение
2
qv r
t
C1 ln r C2
4
(1)

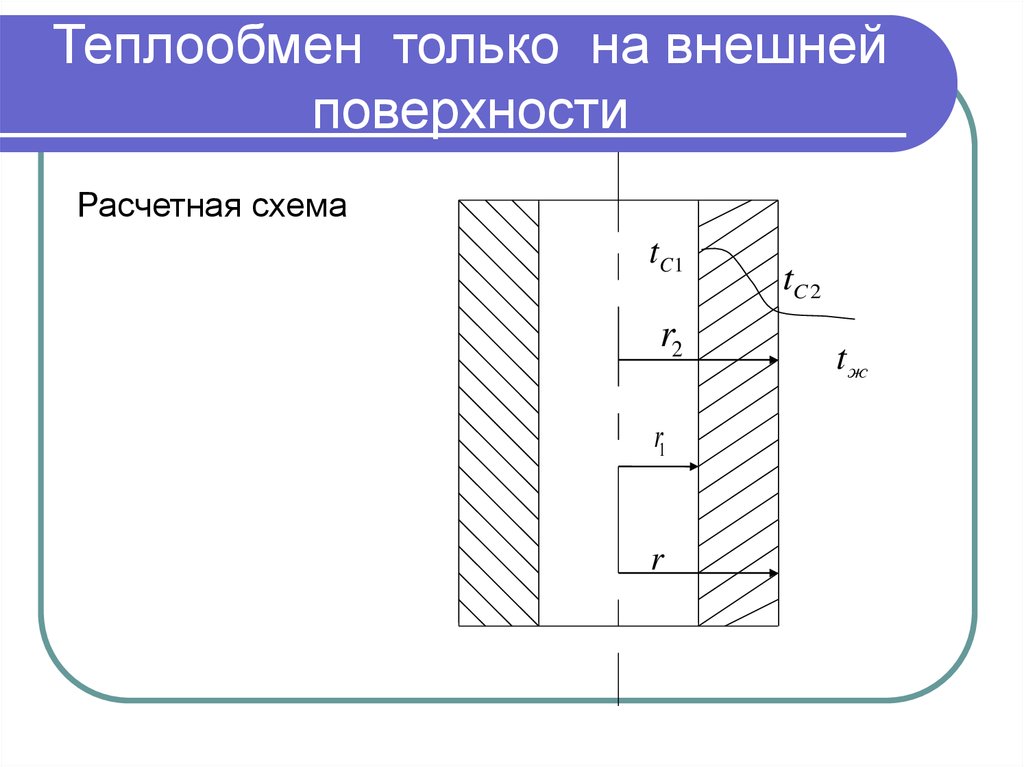
29. Теплообмен только на внешней поверхности

Расчетная схема
tC 1
r2
r1
r
tC 2
tж

30. Теплообмен только на внешней поверхности

Граничные условия:
dt
dr
dt
dr
r r2
0,
r r1
tс 2 t ж 2

31. Теплообмен только на внешней поверхности

Найдем константы
1 qV r1
C1
0
r1 2
dt
1 qV r
C1
,
dr
r 2
qV r 21
C1
,
2

32. Теплообмен только на внешней поверхности

Температура на внешней поверхности:
2
2
1
qV r 2 qV r
tс 2
ln r2 c2
4
2
Из второго граничного условия:
qV r2 q r
tс 2 t ж 2
2 2 r2
2
V 1
2
V 1
qV r2 q r
tс 2 t ж 2
2 2 r2

33. Теплообмен только на внешней поверхности

Избавимся от неизвестной температуры на внешней поверхности,
приравняв правые части уравнений, и найдем вторую константу:
2
2
1
2
V 1
qV r 2 qV r
qV r2 q r
ln r2 c2 tж 2
4
2
2 2 r2
2
V 1
2
2
1
qV r2 q r
qV r 2 qV r
c2 tж 2
ln r2
2 2 r2
4
2

34. Теплообмен только на внешней поверхности

Частное решение:
qV r2
r1
1
t tж2
2 r2
2
2
2
qV r2
r1
r
r
1 2 ln
4 r2
r2 r2
2

35. Теплообмен только на внешней поверхности

Температура на внешней поверхности:
qV r2 r1
1
2 r2
2
tс 2 tж2

36. Теплообмен только на внешней поверхности

Плотность теплового потока на внешней поверхности:
q tс2 tж2
qV r2 r1
1
2 r2
2

37. Теплообмен только на внешней поверхности

Температура на внутренней поверхности:
tс1 tж2
r1
qV r2
1
2 r2
2
qV r2
r1
r1
r1
1 2 ln
4 r2
r2 r2
2
2
2

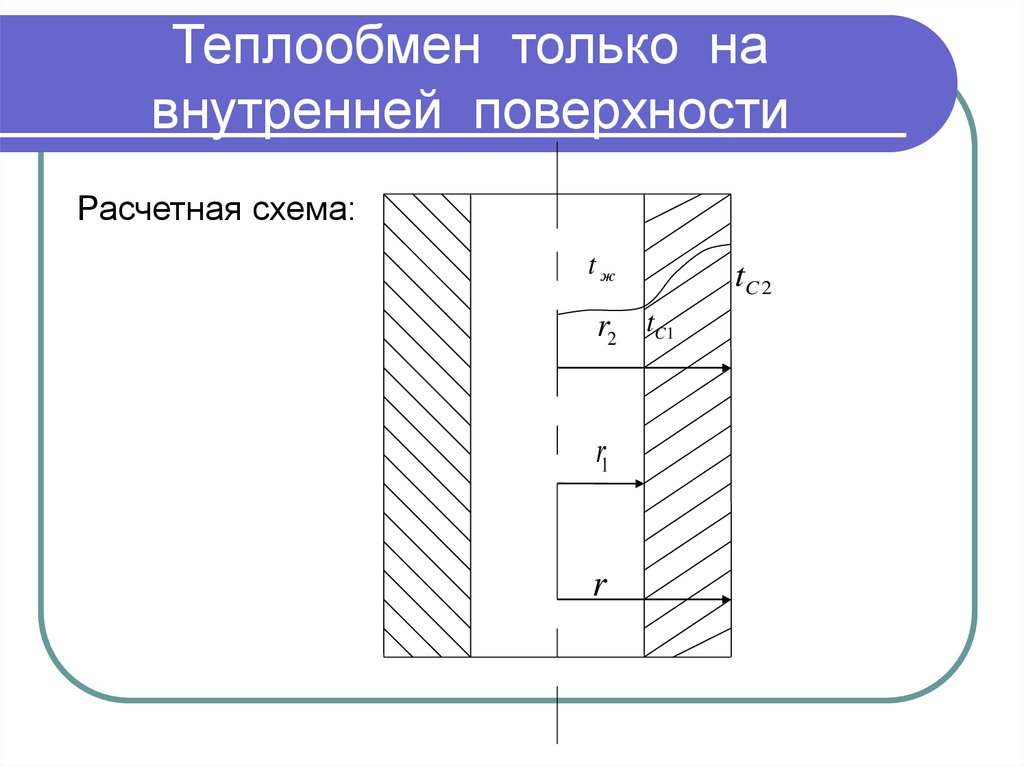
38. Теплообмен только на внутренней поверхности

Расчетная схема:
tж
r2 tC1
r1
r
tC 2

39. Теплообмен только на внутренней поверхности

Граничные условия:
dt
dr
dt
dr
r r1
0,
r r2
tс1 tж1

40. Теплообмен только на внутренней поверхности

Найдя константы, получим частное решение:
qV r1 r2
1
t tж1
2 r1
2
qV r2
r r1 r
2 ln
4
r1 r2 r2
2
2
2

41. Теплообмен на внутренней и наружной поверхности

В этом случае существует максимум температуры
dt
внутри стенки при
r r0
dr
0,
т.е. здесь тепловой поток равен нулю (тепловая
изоляция). Таким образом, можно использовать
полученные ранее решения. Задача сводится к
отысканию значения
.
0
В одном случае следует подставить
,
1
0
в другом
r r
r2 r0
r r

42. Теплообмен на внутренней и наружной поверхности

Находим r0 :
2
qV r0 r2
r2
2 ln 1 ;
t0 tс 2
r0
4 r0
2
2
r0
qV r0 r1
2 ln 1 ;
t0 tс1
r1
4 r0
2

43. Теплообмен на внутренней и наружной поверхности

Вычитаем из первого уравнения второе:
tс1 tс 2
qV r0 r2 r1
r0
r0
2 ln 2 ln ;
4 r0 r0
r2
r1
2
2
2

44. Теплообмен на внутренней и наружной поверхности

Найдем r0 :
qV r2 r
2
r0
2
2
1
4 t
r
r2
qV 2 ln
r1
с1
tс 2

45. Теплообмен на внутренней и наружной поверхности

Зная r0 , легко находим
распределение
температуры во
внутреннем и наружном
слое по соответствующим
формулам.

46. Вопросы к экзамену

1.
2.
3.
4.
Стационарная теплопроводность в однородной
пластине при наличии внутренних источников
теплоты.
Стационарная теплопроводность в однородном
цилиндрическом стержне при наличии
внутренних источников теплоты.
Стационарная теплопроводность в
цилиндрической стенке при наличии внутренних
источников теплоты (теплота отводится только
через внутреннюю поверхность).
Стационарная теплопроводность в
цилиндрической стенке при наличии внутренних
источников теплоты (теплота отводится только
через внешнюю поверхность).