3сем_Лк 11_3_Функц р_Степ ряд

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы
Екатерины II
Лекция 3
Функциональные ряды
Степенной ряд
04.12.2025
г. СанктПетербург
2025
1/12

2.

Функциональные ряды (ФР): члены функции от х
u ( x)
u1 ( x) u 2 ( x) u 3 ( x) …=
Область
сходимости ФР –
n
n 1
множество значений х,
при которых числовые
ряды сходятся
n
Остаток ФР
Пример 1. Найти
область сходимости
х 2
х 1
n 1
n
Частичная сумма S (х)
При конкретном значении
аргумента х – числовой ряд
Sn ( x)
Сумма ФР S(х) nlim
uk ( x )
k 1
Rn ( x)
u ( x) S ( x) S n ( x)
k
k n 1
n
Rn ( x) 0
u ( x) – сходится nlim
k
k 1
2|12
n
u ( x)
n
n 1

3.

Пример 2. Исследовать
на сходимость
u n ( x)
cos nх
n
2
1
2
n
cos nх
2
n
n 1
cos nх
un(х)=
n2
- общий член ряда
1
– сходится (ряд Дирихле, р=2)
2
n 1 n
х (– , )
абсолютно
u ( x) – сходится
х (– , )
ФР равномерно сходится на a,b , если:
u n (x) – сходится
1
n
n 1
0 найдется положительное число N ( ) 0 :
такое, что n N выполняется неравенство:
s ( x) S n ( x) Rn ( x)
S n x
х a,b
равномерно сходится к S(x): номер N зависит только от
3|12

4.

u n x
n 1
мажорируется в некоторой области x X
,
если существует положительный сходящийся числовой ряд
x X
u n x a n
Теорема (признак
Вейерштрасса) x X u n x a n
Доказательство.
n 1
мажорантный
ряд
a – сходится
n
n 1
S n S lim R n 0
a n – сходится nlim
n
a
n 1
u ( x) равномерно
сходится
n
n 1
0 N ( ) 0 : n N S S n Rn ( x X )
u n x a n R n x R n ( x X ) ФР равномерно сходится
4|12
n

5.

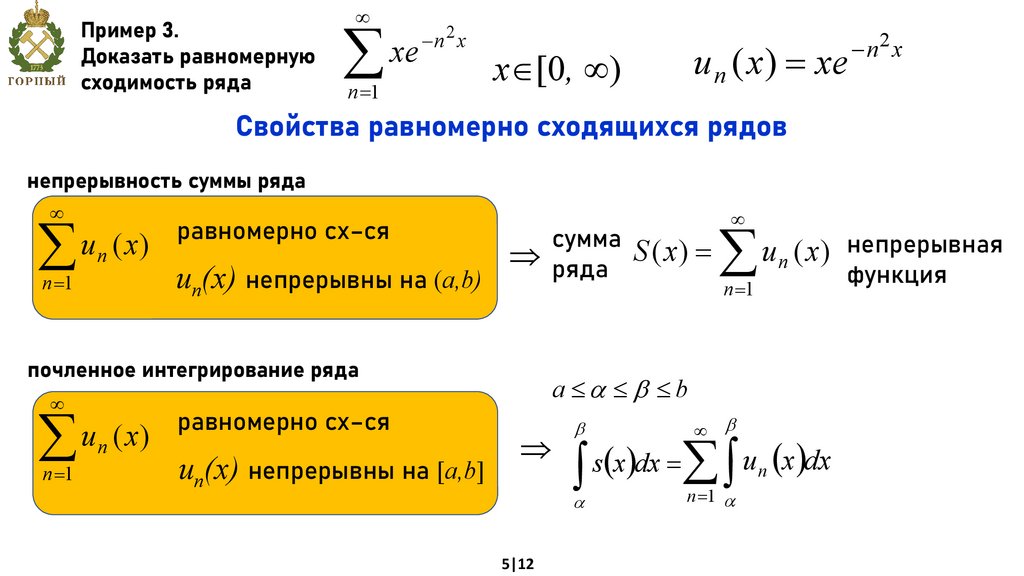
Пример 3.
Доказать равномерную
сходимость ряда
xe
n2 x
n 1
u n ( x) xe
х [0, )
n2 x
Свойства равномерно сходящихся рядов
непрерывность суммы ряда
u n ( x)
n 1
равномерно сх–ся
un(x) непрерывны на (a,b)
сумма
ряда S ( x)
почленное интегрирование ряда
u ( x) u (x) непрерывны на [a,b]
равномерно сх–ся
n
n 1
n
u n ( x) непрерывная
функция
n 1
a b
5|12
s x dx
u x dx
n
n 1

6.

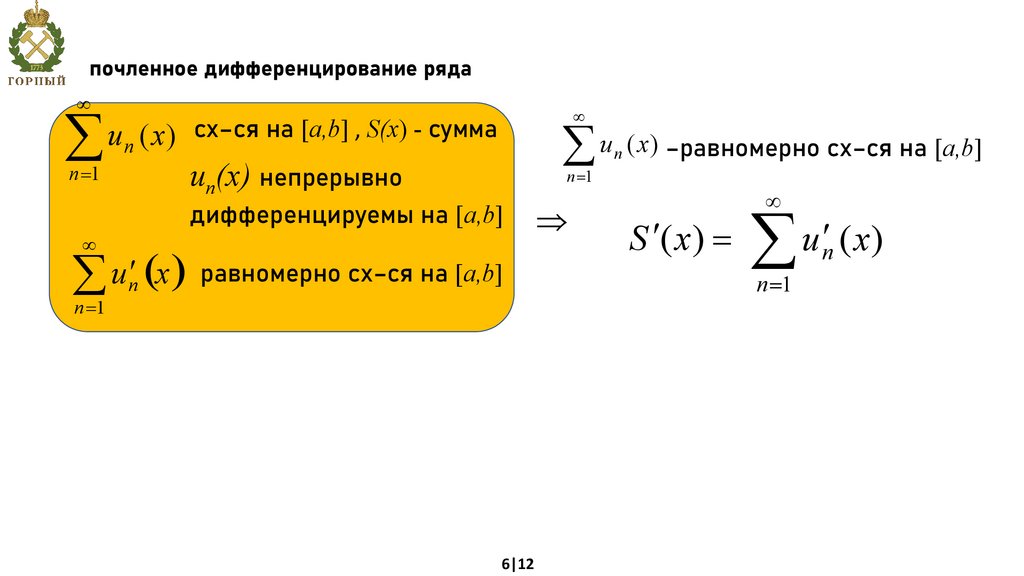
почленное дифференцирование ряда
u n ( x) сх–ся на [a,b] , S(x) - сумма
u ( x) –равномерно сх–ся на [a,b]
n
un(x) непрерывно
n 1
n 1
дифференцируемы на [a,b]
¥
å u ¢ (x ) равномерно сх–ся на [a,b]
n =1
n
6|12
S (x)
n 1
u n ( x)

7.

Степенной
n
2
n
c
x
c
c
x
c
x
ряд
n 0 1 2 +… cn x +… (1)
n 0
n 0
c n ( x а)
При х=0 ряд (1) – сходится
n
(2)
При х=а ряд (2) – сходится
Теорема Ряд (1) сходится при
(Абеля). некотором х=х0 0
ряд (1) абсолютно сх–ся
х : x x 0
Ряд (1) расходится при ряд (1) расходится
некотором х=х1
х : x x1
7|12

8.

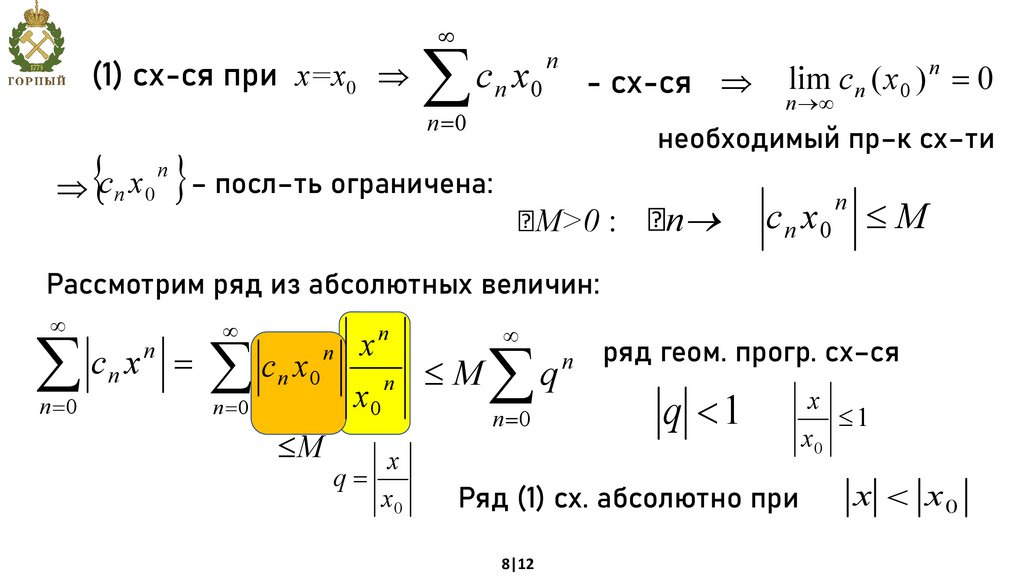
(1) сх-ся при х=х0
c x
n
- сх-ся
n 0
n 0
c n x0
n
– посл–ть ограничена:
n
lim c n ( x 0 ) 0
n
необходимый пр–к сх–ти
М>0 : n
n
c n x0 М
Рассмотрим ряд из абсолютных величин:
n 0
n
cn x
c x
n 0
n 0
М
n
x
n
x0
n
x
q
x0
M
q
n 0
n
ряд геом. прогр. сх–ся
q 1
Ряд (1) сх. абсолютно при
8|12
x
1
x0
x x0

9.

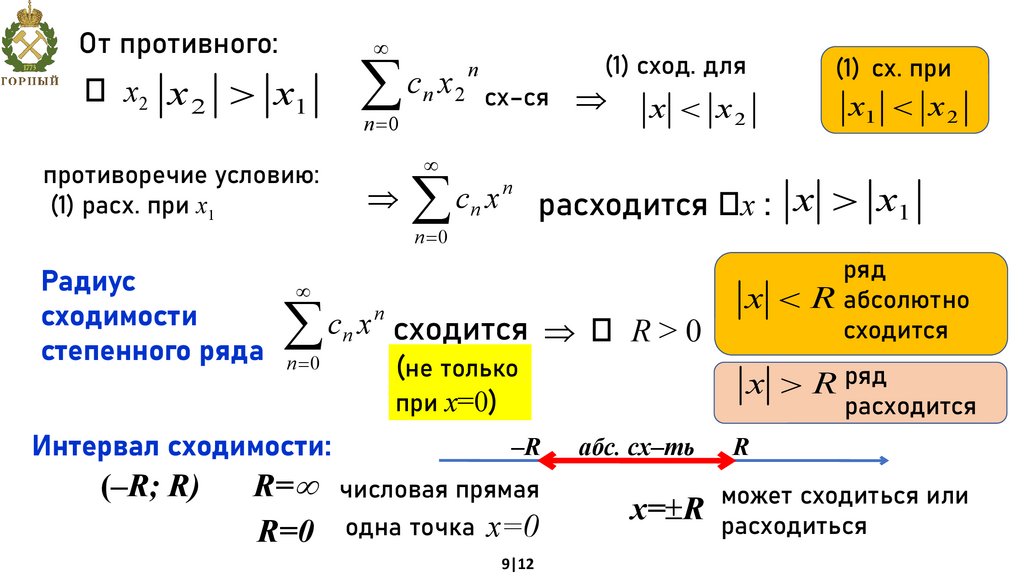
От противного:
х2 x 2 x1
противоречие условию:
(1) расх. при х1
c x сх–ся
n
n
2
n 0
(1) сход. для
(1) сх. при
x x2
x1 x 2
c x расходится х : x x
n
n
1
n 0
Радиус
n
сходимости
c n x сходится R > 0
степенного ряда n 0
(не только
Интервал сходимости:
(–R; R)
R=
R=0
при x=0)
ряд
x R абсолютно
сходится
x R ряд
расходится
–R
числовая прямая
одна точка х=0
9|12
абс. сх–ть
R
может сходиться или
х= R расходиться

10.

Как найти радиус и интервал сходимости ст. ряда?
cn x
–R абс. сх–ть R
n
c ( x а)
n
0
n 0
n
n 0
l
R
c n 1
u n 1 ( x)
1
x l <1 x
lim
x lim
n c
n u ( x )
l
n
n
u n ( x) c n x
n
1
0
10|12
а
cn
R lim
n c
n 1
1
0
R
1
lim n u n ( x) x lim n c n x k <1 x
n
n
k
k
a–R абс. сх–ть a+R
R lim
n n
1
cn

11.

Теорема (свойство Степенной ряд сходится равномерно на любом
степенных рядов). отрезке [–k; k], 0 k<R
R>0
ряд абсолютно
сходится x R
c k сходится
x k R
n абсолютно
n
n 0
мажорантный ряд
cn х
n
n
cn k
Пример 4. Найти область
сходимости ст. ряда
n
x
n
n 0 10 n 1
11|12
n 1
x 2
n
n
2

12.

Спасибо за внимание
Санкт-Петербургский горный
университет
императрицы Екатерины II,
199106, г. Санкт-Петербург,
Малый пр. В.О., д. 83
Тел.: +7(812) 328-82-98;
12|12