Similar presentations:
Числовые, функциональные и степенные ряды
1. ТЕМА 10. Числовые, функциональные и степенные ряды.
2.
Числовым рядом называется сумма вида:u
n 1
n
u1 u2 u3 ... un ...
где числа u1, u2, u3,…,un,... – члены ряда
(бесконечная последовательность),
un – общий член ряда.
Частичные суммы ряда:
S1=u1,
S2=u1+u2,
S3=u1+u2+u3,
…………………..
Sn=u1+u2+u3+…+un
3.
Еслиlim S n S или
n
lim (u1 u2 ... un ) S ,
n
то ряд называется сходящимся, а число S –
суммой сходящегося ряда.
u
n 1
n
u1 u2 ... un ... S
Если
частичная
сумма
Sn
ряда
при
неограниченном возрастании n не имеет
конечного предела (в частности, стремится к
+∞ или к -∞), то такой ряд называется
расходящимся.
4.
Пример.Найти сумму членов ряда:
Находим частичные суммы членов ряда:
5.
Запишем последовательность частичных сумм:Общий член этой последовательности есть:
…
n/(2n+1)
Последовательность частичных сумм имеет предел,
равный 1/2. Итак, ряд сходится и его сумма равна 1/2.
6.
unРяд
может сходиться только при условии,
n 1
что его общий член un при неограниченном
увеличении номера n стремится к нулю:
lim un 0
n
Если lim u n 0 , то ряд u n расходится – это
n 1
n
достаточный признак расходимости ряда.
7.
а)Признак сравнения рядов с положительными
членами.
Исследуемый ряд сходится, если его члены не превосходят
соответствующих членов другого, заведомо сходящегося
ряда: исследуемый ряд расходится, если его члены
превосходят соответствующие члены другого заведомо
расходящегося ряда.
б) Признак Даламбера.
Если для ряда с положительными членами
u
u1 u2 ... un un 1...(un 0)
n 1
u n 1
выполняется условие lim
l , то ряд сходится при l<1 и
n u
расходится при l>1.
n
n
Признак Даламбера не дает ответа, если l=1. В этом
случае для исследования ряда применяют другие приемы.
8.
-образован из членов геометрической прогрессии:n
2
n
aq
a
aq
aq
...
aq
...
n 0
(a 0)
сходится при |q|<1
расходится при |q|≥1
9.
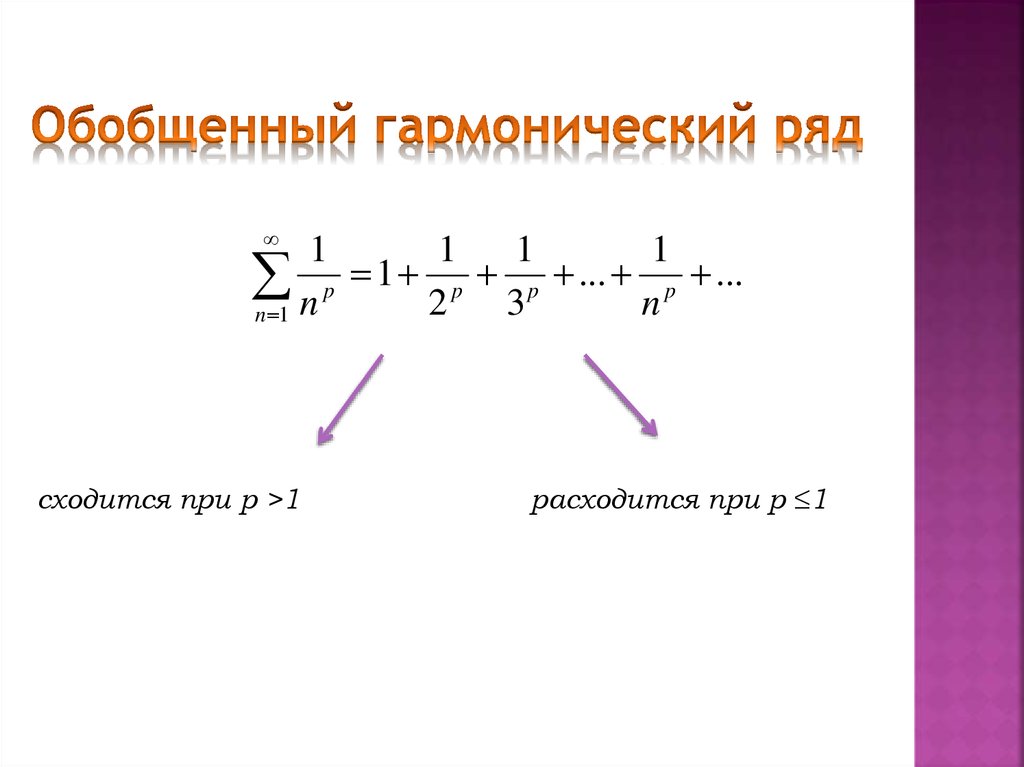
11
1
1
1 p p ... p ...
p
2
3
n
n 1 n
сходится при p >1
расходится при p ≤1
10.
Пример.Исследовать
сходимость
ряда,
применяя
необходимый признак сходимости и признак сравнения:
1
1
1
1
1
...
...
n
2
3
n
1 2 3 2 5 2
(2n 1) 2
n 1 ( 2n 1) 2
1
lim un lim
0
n
n
n ( 2n 1) 2
Необходимый признак сходимости ряда выполняется. Для
признака сравнения сравним данный ряд с геометрическим:
1
1 1
1
1 2 ... n ...
n
2 2
2
n 0 2
который сходится, так как q=1/2<1.
11.
Сравнивая члены нашего ряда с соответствующимичленами геометрического ряда, получим неравенства:
1
1
1 1
1
1
1
1;
2;
3 ;...;
n ;...
2
3
n
2
3 2
2 5 2
2
(2n 1) 2
2
Т.е. члены данного ряда соответственно меньше членов
геометрического
ряда.
Следовательно,
данный
ряд
сходится.
12.
Пример. Исследовать сходимость ряда, используя признакДаламбера:
Следовательно, данный ряд сходится.
13. Основные понятия
Определение 1:Функциональным называется ряд, члены которого есть
непрерывные функции от аргумента x:
u1 ( x) u2 ( x) ... un ( x) ... un ( x)
n 1
При x=n функциональный ряд становится числовым,
который либо сходится, либо расходится.
14. Пример функционального ряда
Рассмотрим геометрическую прогрессиюсо знаменателем х:
2
3
n
1 x x x ... x. ...
Геометрическая прогрессия сходится,
если ее знаменатель x 1 . Тогда она
имеет сумму S 1
, которая
1 x
очевидно является функцией от х.
15. Основные понятия
Определение 2:Совокупность значений x, при которых ФР сходится,
называется областью сходимости ряда.
Сумма ФР может быть представлена:
S ( x) S n ( x) Rn ( x)
S n ( x) u1 ( x) u2 ( x) ... un ( x)
Rn ( x) un 1 ( x) un 2 ( x) ...
16.
Определение 3:ФР называется равномерно сходящимся в некоторой
области X, если для каждого сколь угодно малого ε>0
найдется такое N(ε)>0, что при n>N выполняется
неравенство:
S ( x) Sn ( x) Rn ( x) x X
S(x) – непрерывная функция
17.
Определение 4:Пусть даны:
u ( x) функционал ьный
n 1
n
ряд
a
n 1
n
знакополож ительный числовой ряд
причем в некоторой области выполняется условие:
u1 ( x) a1 , u2 ( x) a2 ,..., un ( x) an ,...
Тогда
a
n 1
n
является мажорантой для un ( x)
n 1
18. Признак Вейерштраса
Если мажоранта функционального ряда сходится,то сходится и функциональный ряд абсолютно и
равномерно.
19. Свойства абсолютно и равномерно сходящихся рядов
Пусть даны функциональные ряды:u ( x) S ( x)
n 1
n
равномерно сходящийся на a; b
v ( x) S ( x), ( x) S ( x) равномерно сходящиеся, причем :
n 1
n
1
n 1
n
2
b
v ( x) un\ ( x) и n ( x) un ( x)dx тогда :
n
a
b
S1 ( x) S \ ( x)
S 2 ( x) S ( x)dx
a
20. Степенные ряды
Определение 5:Функциональный ряд вида:
n
0
1
2
n
a
x
a
x
a
x
a
x
...
a
x
..
n
0
1
2
n
n 0
a0 ,a1 ,...an вещественные числа
называется степенным рядом.
21. Теорема Абеля
1.Если степенной ряд сходится при x = x1, то он
сходится для всех |x| < |x1|.
2.
Если степенной ряд расходится при x = x2, то он
расходится для всех |x |> |x2|.
Из теоремы следует, что существует такое
положительное значение x = R, что при |x| < R
степенной ряд сходится,
а при |x| > R расходится, R - радиус сходимости.
Ряд сходится
x0 - R
x0
x0 + R
22. Нахождение радиуса сходимости
1.По признаку Даламбера:
un 1
an
R lim
lim
n u
n a
n
n 1
23. Нахождение радиуса сходимости
2.По радикальному признаку Коши:
R
1
lim n an
n
24. Ряд Тейлора
Определение 6:Рядом Тейлора функции f(x) называется степенной ряд
вида:
f \ ( x0 )
f \ \ ( x0 )
f ( n) ( x0 )
2
f ( x) f ( x0 )
( x x0 )
( x x0 ) ...
( x x0 ) n ...
1!
2!
n!
это есть разложение функции в окрестности точки x0.
Коэффициентами являются производные высших
порядков в точке x0, т.е. Для разложения в ряд
Тейлора необходимо, чтобы f(x)существовала в x0
вместе со своими производными.
25. Достаточное условие разложения функции в ряд Тейлора
Определение 6:Всякая функция f(x) бесконечно дифференцируемая в
интервале |x-x0|<r может быть разложена в
степенной ряд Тейлора, если в этом интервале
остаток ряда стремится к нулю:
lim Rn ( x) 0
n
f ( n 1) (c)
Rn ( x)
( x x0 ) n 1
(n 1)!
26. Ряд Маклорена
Определение 7:Рядом Маклорена функции f(x) называется степенной
ряд вида:
f \ (0)
f \ \ (0) 2
f ( n ) (0) n
f ( x) f (0)
x
x ...
x ...
1!
2!
n!
это есть разложение функции в окрестности точки x=0.
Коэффициентами являются производные высших
порядков в точке x=0, т.е. Для разложения в ряд
Маклорена необходимо, чтобы f(x)существовала в
x=0 вместе со своими производными.
27. Степенные ряды
Определение. Рядa x
n 0
n
n
a0 a1 x a2 x ... an x ...
2
n
называется степенным по степеням х . Ряд
.
является степенным по степеням
n
2
a
x
x
a
a
x
x
a
x
x
n
0
0
1
0
2
0 ... an
n 0
x x0 n ...
x x0
28. Интервал сходимости степенного ряда
Для любого степенного ряда существуетконечное неотрицательное число R радиус сходимости - такое, что
R если
0
, тоx при
x R
R
ряд сходится, а при
расходится. R, R
Интервал
называется
R
интервалом сходимости степенного
ряда. Если
, то интервалR 0
сходимости представляет собой всю
числовую прямую. Если же
, то
степенной ряд сходится лишь в точке
х=0.
29. Нахождение интервала сходимости по признаку Даламбера
Составим ряд из абсолютных величинчленов степенного ряда и найдем
интервал, в котором он будет
сходиться, Тогда в этом интервале
данный степенной ряд будет сходиться
абсолютно. Согласно признаку
n 1
Даламбераu,n если
an 1 x
1
lim
lim
1
n
n u
n
an x
n
,то степенной ряд абсолютно сходится
для всех х, удовлетворяющих этому
условию.
30. Продолжение
В этом случае ряд будет сходитьсявнутри интервала (-R,R),где R-это
радиус сходимости ряда: a
n
R lim
n a
. n 1
За пределами этого интервала ряд
будет расходиться, а на концах
nгде
1
интервала,
an 1 x
1
lim
n
n
an x
, требуется
дополнительное исследование.
31. Примеры
Найти интервал сходимости рядаn
x
.
n 0 2n 1
Следовательно, ряд сходится абсолютно в
интервале (-1,1).
x n 1 2n 1
2n 1
2n
lim x
x lim
x 1
lim
n
2n 3
n 2n 3 x
n
n 2n
32. Примеры
Положимряд
Тогда получим числовой
x . 1
1. Этот ряд расходится
n 0 2 n 1
(сравните его с гармоническим рядом).
Полагая x = -1, имеем знакочередующийся
ряд
,
1 n
который сходится условно в силу
теоремы
n 0 2n 1
Лейбница.
Итак, степенной ряд сходится в
промежутке [-1,1).
33. Примеры
Найти интервал сходимости степенногоxn
x n,
x n. Здесь
un
n! 1 2 3 ... n
n 1 n!
.Тогда
n 1 =
n 1
x
x
un 1
n =1 ! 1 2 3 ... n n 1 =
ряда
=
lim
n
u n 1
un
lim
x
n 1
1 2 3 ... n
n 1 2 3 ... n
n 1 x
n
lim
n
x
n 1
34. Продолжение
1x 0 0 .
= x lim
n n 1
Но 0<1 всегда, т.е. независимо от x. Это
означает, что степенной ряд сходится
независимо от x, т.е. на всей числовой
прямой.
Итак, интервал сходимости ряда - это
промежуток
.
,
35. Пример
Найти интервал сходимости рядаlim
n 1 ! x
n
n! x
n
n 1
= lim
1 2 3 ... n n 1 x
n
1 2 3 ... n
n.! x
n 1
=
= lim n 1 x = x lim n 1 .
n
n
Этот предел может быть меньше
единицы, если только x=0 (иначе он
будет равен бесконечности). Это
означает, что степенной ряд сходится
лишь в точке x=0.
n
36. Свойства степенных рядов. Непрерывность суммы ряда
1. Сумма степенного рядаS ( x) a 0 a1 x a 2 x 2 ... a n x n ...
является непрерывной функцией в каждой
точке интервала сходимости этого ряда.
Например,
непрерывна , если
.
1
2
3
n
S ( x)
1 x x x ... x ...
1 x
x 1
37. Почленное дифференцирование
2. Ряд, полученный почленнымдифференцированием степенного ряда,
является степенным рядом с тем же
интервалом сходимости, что и данный ряд,
причем :если
,
то S ( x) a a x a x 2 ... a x n ...
0
1
2
n
2
n 1
S ( x) a1 2a 2 x 3a3 x ... na n x ...
38. Почленное интегрирование
3. Степенной ряд можно почленноинтегрировать на любом промежутке,
целиком входящем в интервал сходимости
степенного ряда, при этом
где S ( x)dx
a0 dx . a1 xdx ... an x dx ...
n
( , ) ( R, R)
39. Определения
Определение. Если бесконечнодифференцируемая функция является
суммой степенного ряда, то говорят,
что она разлагается в степенной ряд .
Опр. Рядом Тейлора функции f(x)
называется ряд, коэффициенты
которого определяются
f ( n ) ( x0 )
an
(n)
n ! f ( n ) ( 0)
f
(
x
)
по формулам
, т.е. ряд
0
n
( x x0 ) n
x
n
!
n 0
или n 0 n !
.
40. Степенной ряд как ряд Тейлора
Теорема. Если в некоторой окрестноститочки
x
0
,
n
f
(
x
)
a
a
(
x
x
)
...
a
(
x
x
)
..
0
1 ее ряд
0 Тейлора.
n
0
то ряд справа
есть
Короче: если функция представлена в
виде степенного ряда, то этот ряд является
ее рядом Тейлора.
Представление функции ее рядом
Тейлора единственно.
41. Формула Тейлора
Рассмотрим n-ю частичную сумму рядаТейлора:
(n)
f ( x0 )
f ( x0 )
n
S
(
x
)
f
(
x
)
(
x
x
)
...
(
x
x
)
n
0
0многочленом
0
Этот
многочлен
называется
1!
n!
Тейлора функции
.
Разность
называетсяf (x )
остаточным членом
R ( x) ряда
f ( x) Тейлора.
S ( x)
n
n
42. Формула Тейлора с остаточным членом в форме Лагранжа
Остаточный член в форме Лагранжа имеетвид:
f ( n 1) (c)
Rn ( x)
( x x0 ) n 1 , где c ( x0 , x)
(n 1)!
Тогда
( n 1)
f ( x0 )
f ( n ) ( x0 )
f
(c )
fназывается
( x) f ( x0 ) формулой
( x x0 ) ...Тейлора
(с
x x0 ) n
( x x0 ) n 1
1!
n!
(n 1)!
остаточным членом в форме Лагранжа.
43. Условия сходимости ряда Тейлора к функции у=f(x)
Для того чтобы функцию можно былоразложить в ряд Тейлора на интервале(R,R),необходимо и достаточно, чтобы
функция на этом интервале имела
производные всех порядков и чтобы
остаточный член формулы Тейлора
стремился к нулю при всех
x ( R, R) при n
44. Достаточные условия разложимости функции в ряд Тейлора
Если функция f(x) на интервале (-R,R)бесконечно дифференцируема и ее
производные равномерно ограничены в
совокупности, т. е. существует такая
константа М, что для всех
выполняется условие
x ( R, R) при п=0,1,2,…, то функцию
можно
( n ) разложить в ряд Тейлора на этом
f ( x) M
интервале.
45. Разложение
f ( x) ex
Все производные этой функции
совпадают с самой функцией, а в точке
х=0 они равны 1. Составим для
2 Маклорена:
n
функции формально
ряд
x x
x
1
1
2!
...
n!
...
Этот ряд, очевидно, сходится на всей
числовой оси. Но все производные
( n 1)
функции
равномерно ограничены,
f
(c )
т. к.
, где R-любое
число из интервала сходимости.
x
Поэтому этот ряд сходится
именно к
e .
функции
e e
c
R
46. Разложение в ряд синуса.
Вычислим производные синуса:f ( x) cos x sin( x
f ( x) cos( x
2
f (0) 0,
f (0) 1,
)
) sin( x 2 )
2
2
f ( x) cos( x 2 ) sin( x 3 )
2
2
.......................................................
f
(n)
( x) sin( x n ).
2
f (0) 0
f (0) 1
f ( 4 ) ( 0) 0
..................
f ( 2 n 1) (0) ( 1) n 1
........................
47. Продолжение
Ясно, что все производные синуса непревосходят по модулю единицу. Так что
запишем ряд, который будет разложением
синуса:
2 n 1
2 n 1
x3 x5
x
x
sin x x
... ( 1) n
.. ( 1) n
,
! 5! что этот( 2ряд
n 1)!
n 0
при этом 3видно,
сходится
на ( 2n 1)!
всей числовой оси.
48. Приближенное вычисление интегралов
Разложения 1–7 позволяют, используясоответствующее разложение,
вычислять приближенно значения
функций, интегралы, приближенно
интегрировать дифференциальные
уравнения.
Пример . С помощью степенного ряда
1
вычислить с точностью до 0,0001
x2
e
0
dx
49. Решение
Разложим подынтегральную функцию встепенной ряд:
e x
1
2
2 2
2 3
2 4
(
x
)
(
x
)
(
x
)
2
1 x
...
2!
3!
4!
1
4
6
8
x
x
x
x
2
e
dx
(
1
x
...)dx
0
0
2 ! 3! 4 !
1
1
1
1
1
4
6
8
x
x
x
dx x 2 dx
dx
dx dx ...
2!
3!
4!
0
0
0
0
0
2
3
x
x 10
3
1
0
x5
2 5
1
0
x7
6 7
1
0
x9 1
0 ..
24 9
50. Продолжение
35
7
x
x
x
1
1
x 10
0
0
3
2 5
6 7
1 1
1
1
1
..
3 10 42 216
1
0
x9 1
0 ..
24 9
Так как получившийся ряд является
знакочередующимся, то сумма знакочередующегося
ряда не превосходит первого члена такого ряда. Ясно,
что часть ряда, которую в задаче следует отбросить,
также является знакочередующимся рядом и его сумма
не превзойдет модуля первого отброшенного члена
ряда.
Таким образом, первый отброшенный член ряда
должен быть меньше заданной погрешности, т.е.
0,0001.
51. Продолжение
Вычислив еще несколько членов ряда1
1
1
,
,
1320 9360 75600
видим, что
1
0,0001
75600
Отбросив этот и следующие за ним члены
ряда, получим:
1
e
0
x2
1 1
1
1
1
1
dx 1
0,7468
3 10 42 216 1320 9360
52. Приближенное вычисление значений функций
Вычислить 3 10 с точностью до0,001.Преобразуем
1
10
2
3
3
3
10 8 2 1 23 1 0,25 2(1 0.25) 3
8
8
Воспользуемся биномиальным рядом при
х=0,25 и m 1 .
3
Получим
1 1
1 1
1
( 1)
( 1)( 2)
1
3
3
10 2(1 0,25 3 3
0,25 2 3 3
0,25 3 )
3
2!
3!
2(1 0,0833 0,0069 0,0009) 2(1 0,0833 0,0069)
2,1528 2,153.



















































 mathematics
mathematics








