2_1 Векторы24

1.

Раздел 6. ЭЛЕМЕНТЫ
ВЕКТОРНОЙ АЛГЕБРЫ
§ 1. Векторы на плоскости и в
пространстве. Линейные операции
над векторами. Проекция вектора на
ось.

2.

При изучении различных явлений природы встречаются
величины, которые полностью определяются заданием их
числовых значений. Такие величины называются скалярными
(или скалярами).
Примером скаляров являются
температура, время, работа и т.д.
длина,
площадь,
объем,
Помимо скалярных величин встречаются такие, для
определения которых, кроме числового значения требуется
знать также их направление (например, скорость, ускорение
материальной точки). Такие величины называются
векторными.
Векторные величины геометрически изображаются в виде
направленного отрезка, поэтому чаще всего дают следующее
определение вектора.
Опред. Вектором называется направленный отрезок.

3.

Опр. 1. Вектор (свободный вектор) – это математический
объект, характеризующийся величиной и направлением.
Геометрической
интерпретацией
вектора
служит
направленный отрезок, который можно переносить параллельно
самому себе.
B
Вектор обозначается
a , AB
(если задан началом в точке A и концом в точке B).
A
Если точка приложения вектора может быть любой, то есть его
можно переносить, то вектор называется свободным.
Вектор, для которого указана начальная точка, называется
связанным.
Вектор называется скользящим, если его можно перемещать
вдоль прямой, проходящей через начало и конец вектора. Мы
будем рассматривать, как правило, свободные вектора.

4.

Все основные понятия векторной алгебры определяются для
свободных векторов.
Опр. 2. Модулем (длиной) вектора называется длина отрезка,
изображающего вектор. Длина вектора обозначается a , AB .
Опр. 3. Единичным называется вектор, длина которого равна
единице. Единичный вектор обозначают обычно e, e 1.
Опр. 4. Нулевой, или нуль-вектор, – вектор, длина которого
равна нулю (обозначается 0, направление его произвольно).
Направление нулевого вектора не определено, длина его
считается равной нулю.
Опр. 5. Два ненулевых вектора называются равными, если их
модули и направления совпадают.
Т.е. равными будут не только полностью совпадающие векторы,
то есть имеющие общую начальную и общую конечную точки,
но и те, которые можно совместить при помощи параллельного
переноса.

5.

Замечание. Векторы нельзя сравнивать между собой. Запись
вида a b не имеет смысла. Сравнивать можно лишь модули
векторов.
Опр. 6. Векторы a и b, лежащие на одной или параллельных
прямых, называются коллинеарными и обозначаются a b.
Коллинеарные
векторы
могут
быть
направленными (сонаправленными): a b или
противоположно направленными: a b
D
B
M
A
C
N
AB CD
AB MN
одинаково

6.

Рассмотрим два свободных вектора a и b .
Поместим начальные точки этих векторов в одну точку, то
есть a OA b OB
Углом между векторами a и b называется наименьший угол
φ, на который надо повернуть один из векторов до его
совпадения со вторым после приведения этих векторов к
общему началу

7.

Опр. 7. Два коллинеарных вектора называются
противоположными, если их модули равны, а направления
противоположны. a.
a
a
Опр. 8. Векторы a и b, лежащие на перпендикулярных
прямых, называются ортогональными и обозначаются a b.
Нулевой вектор считается как ортогональным, так и
коллинеарным любому вектору.
Опр. 9. Векторы, лежащие в одной или параллельных
плоскостях, называются компланарными.

8.

Линейные операции над векторами
Опр. 10. Суммой двух векторов a и b называется вектор
с a b, начало которого совпадает с началом вектора a , а
конец – с концом вектора b , если начало вектора b совпадает с
концом вектора a.
с a b
b
Правило треугольника
a
Правилом параллелограмма
с a b
b
a

9.

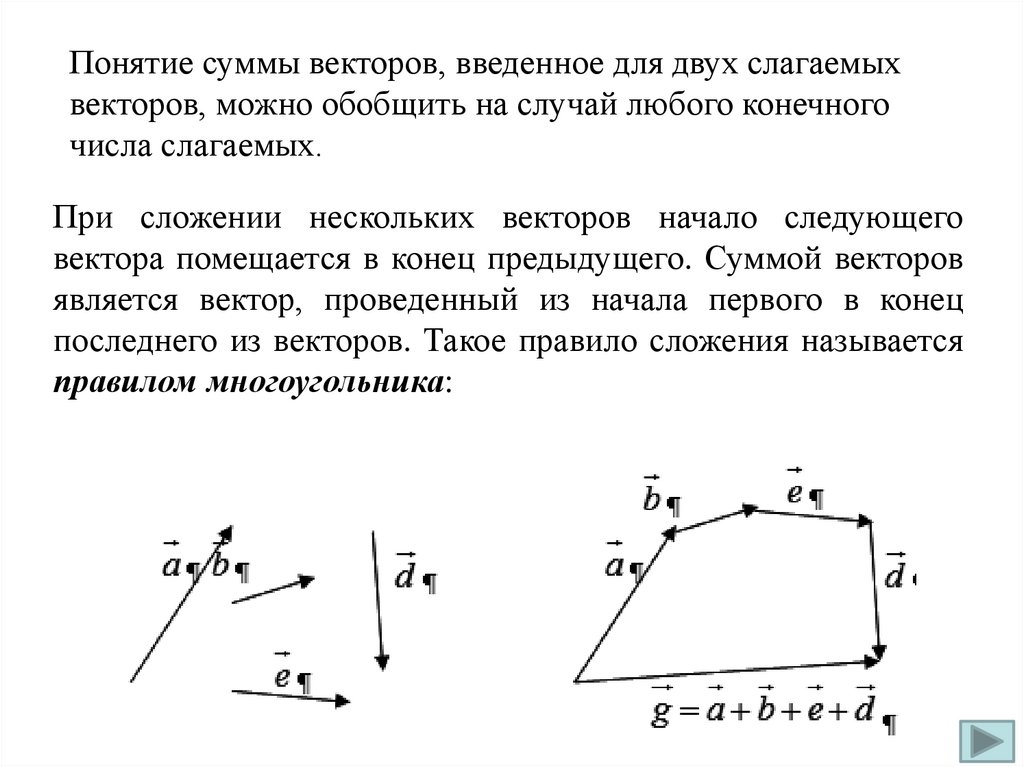
Понятие суммы векторов, введенное для двух слагаемых
векторов, можно обобщить на случай любого конечного
числа слагаемых.
При сложении нескольких векторов начало следующего
вектора помещается в конец предыдущего. Суммой векторов
является вектор, проведенный из начала первого в конец
последнего из векторов. Такое правило сложения называется
правилом многоугольника:

10.

Опр. 11. Разностью векторов a и b называется вектор
d a b a ( b), равный сумме вектора a и вектора b,
противоположного вектору b.
d a b
b
a
Опр. 12. Произведением вектора a на число называется
вектор b a, длина которого равна b a , а направление
совпадает с направлением вектора a , если > 0, и
противоположно направлению вектора a , если < 0.
2a
a
2a

11.

Отсюда следует условие коллинеарности двух векторов:
a b b a.
Основные свойства линейных операций над векторами.
1. a b b a
(коммутативность сложения).
2. a (b c ) (a b) c (ассоциативность сложения).
3. a 0 a.
4. a ( a ) 0.
5. 1 a a.
6. ( a ) ( ) a
(ассоциативность умножения на число).
7. ( a b) a b
(дистрибутивность сложения
векторов относительно умножения на число).
8. ( )a a a
(дистрибутивность сложения
чисел относительно умножения на вектор).

12.

Определение. Векторным пространством называется любое
множество векторов, для элементов которого
а) определена операция сложения (т.е. для каждой пары
векторов a и b , определен третий вектор с a b,
являющийся их суммой;
b)
определена
операция
умножения
вектора
действительное число (т.е. для каждого вектора a
действительного числа α определен вектор a
на
и
c) эти операции обладают 8 основными свойствами
Свойства операций над векторами позволяют обращаться с
ними, как с обычными числами: переносить их из одной части
равенства в другую с противоположным знаком, делить обе
части на ненулевое число, приводить подобные члены и т.п.

13.

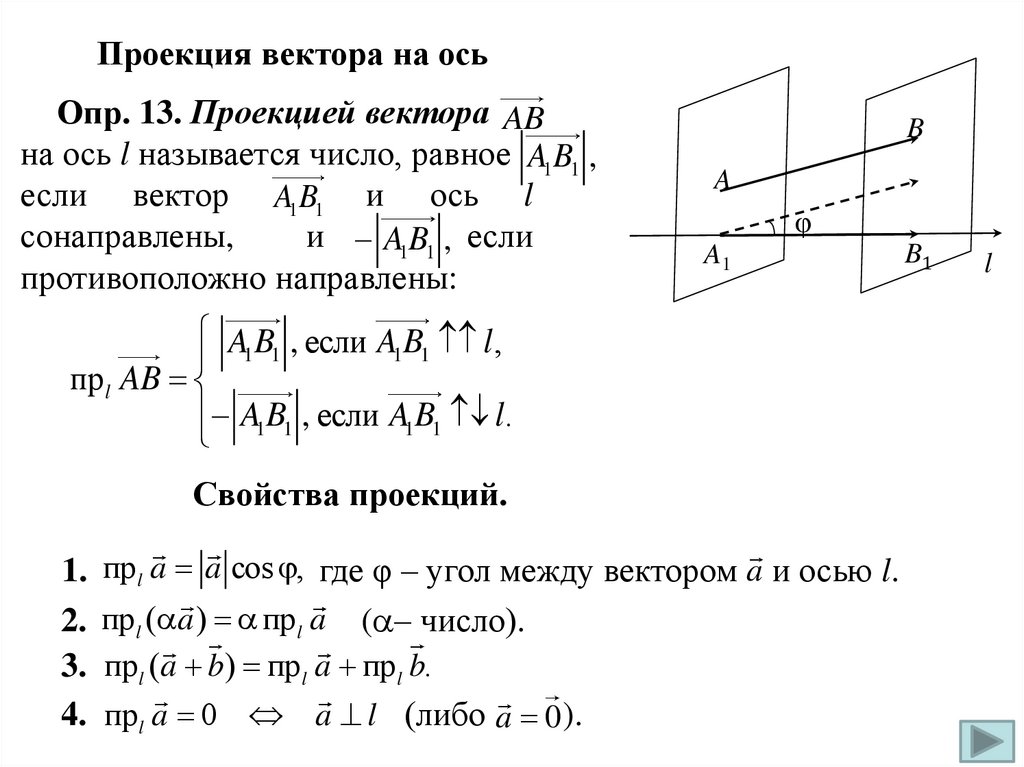
Проекция вектора на ось
Опр. 13. Проекцией вектора AB
на ось l называется число, равное A1B1 ,
если вектор A1B1 и ось l
сонаправлены,
и A1B1 , если
противоположно направлены:
B
A
φ
A1
A1B1 , если A1B1 l ,
прl AB
A1B1 , если A1B1 l.
Свойства проекций.
1. прl a a cos , где φ – угол между вектором a и осью l.
2. прl ( a ) прl a ( – число).
3. прl (a b) прl a прl b.
4. прl a 0 a l (либо a 0 ).
B1
l

14.

§ 2. Линейная зависимость и
независимость векторов. Понятие
базиса.
Опр. 1. Линейной комбинацией векторов a1 , a2 , ..., an
называется любой вектор, равный сумме произведений данных
векторов на некоторые скаляры (числа).
Пример 1. Каждый из векторов r1 a b 2c, r2 2a 3b, r3 2c
является линейной комбинацией векторов a, b, c.
Опр. 2. Векторы a1 , a2 , ..., an
называются
линейно
зависимыми, если существуют такие числа 1, 2, …, n, не все
равные нулю, что 1 a1 2 a2 ... n an 0. Если же это равенство
верно только при 1 = 2 =…= n = 0, то векторы a1 , a2 , ..., an
называются линейно независимыми.

15.

Опред. Если все коэффициенты линейной комбинации равны
нулю α1=α2=…=αn=0, то она называется тривиальной. Если же
среди коэффициентов линейной комбинации найдется хотя бы
один отличный от нуля, то она называется нетривиальной.
Система векторов
называется линейно
a1 , a2 , a3 , ..., an
зависимой, если существует их нетривиальная линейная
комбинация, равная нулевому вектору.
Свойства линейно зависимых и линейно независимых систем
векторов.
С1.Всякая система векторов, включающая нулевой вектор,
является линейно зависимой.
С2.Система векторов, содержащая линейно
подсистему, является линейно зависимой.
зависимую
С3.Всякая подсистема линейно независимой
векторов является линейной независимой.
системы

16.

Утв. 1. Векторы a1 , a2 , a3 , ..., an линейно зависимы тогда и
только тогда, когда один из них является линейной комбинацией
остальных. (Критерий линейной зависимости системы векторов.)
Доказательство.
Необходимость.
a1 , a2 , a3 , ..., an
линейно зависимы
1 , 2 , 3 ,
, n ,
1 a1 2 a2 3 a3 ... n an 0.
2
3
n
a3 ... an ,
Пусть 1 0. a1 a2
1
1
1
a1 является линейной комбинацией a2 , a3 , ..., an .
Достаточность.
a1 2 a2 3 a3 ... n an .
a1 2 a2 3 a3 ... n an 0,
a1 , a2 , a3 , ..., an линейно зависимы. ◄

17.

Критерии линейной зависимости векторов
Тh 1. (О линейной зависимости двух векторов). Два вектора
линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство.
a
b
b a b a 0.
◄
Тh 2. (О линейной зависимости трех векторов).Три вектора
линейно зависимы тогда и только тогда, когда они компланарны.
Упражнение 1. Доказать, что если три вектора линейно
зависимы, то они компланарны.
Теорема. (О линейной зависимости четырех векторов).
Четыре вектора линейно зависимы в пространстве.

18.

Понятие базиса на плоскости и в пространстве
Опр. 3. Базисом на плоскости называются два линейно
независимых вектора этой плоскости, взятые в определенном
порядке.
Опр. 4. Базисом в пространстве называются три линейно
независимых вектора, взятые в определенном порядке.
Тh 3. Если векторы e1 и e2 образуют базис на плоскости, то
любой вектор c этой плоскости может быть единственным
образом представлен в виде линейной комбинации базисных
векторов: c xe1 ye2 .
Доказательство.
M2
c
e2
O
M
e1
M1
c OM OM 1 OM 2 .
Поскольку OM 1 e1 , OM 2 e2 ,
то найдутся такие числа x, y, что
c xe1 ye2 . ◄
OM 1 xe1 , OM 2 ye2 .

19.

Такое представление называется разложением вектора c по
базису e1; e2 , а коэффициенты x, y этого разложения называются
координатами вектора c в базисе e1; e2 .
Тh 4. Если векторы e1 , e2 , e3 образуют базис в пространстве, то
любой вектор c пространства может быть единственным образом
разложен по этому базису:
c xe1 ye2 ze3 ;
тройка чисел x, y, z называется координатами вектора c в базисе
e ; e ; e .
1
2
3
Итак, два любых неколлинеарных вектора образуют базис на
плоскости и три любых некомпланарных вектора образуют
базис в пространстве.

20.

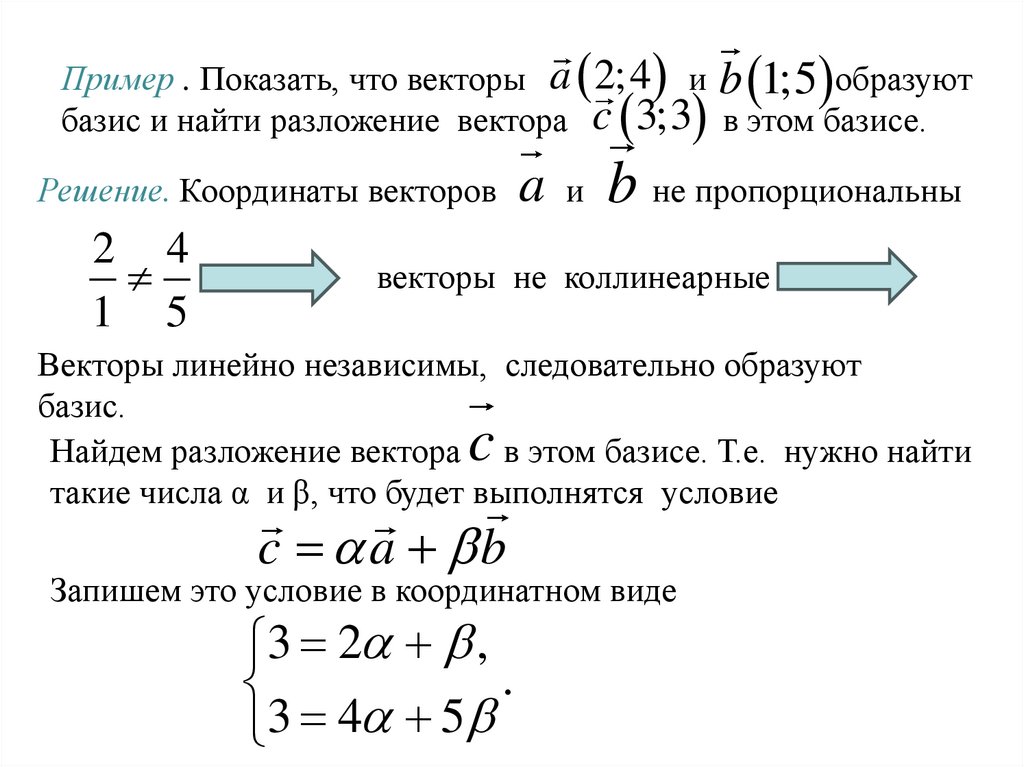
Пример . Показать, что векторы a 2;4 и b 1;5 образуют
базис и найти разложение вектора c 3;3 в этом базисе.
Решение. Координаты векторов a и b не пропорциональны
2 4
1 5
векторы не коллинеарные
Векторы линейно независимы, следовательно образуют
базис.
Найдем разложение вектора в этом базисе. Т.е. нужно найти
такие числа α и β, что будет выполнятся условие
c
c a b
Запишем это условие в координатном виде
3 2 ,
.
3 4 5

21.

6 4 2 ,
.
3 4 5
3 3
1; 2.
Таким образом, мы получили разложение
c 2a b .
c a b
Запишем это условие в координатном виде
3 2 ,
.
3 4 5

22.

§ 3. Декартова прямоугольная система
координат в пространстве. Направляющие
косинусы вектора. Линейные операции над
векторами в координатной форме

23.

§ 3. Декартова прямоугольная система
координат в пространстве. Направляющие
косинусы вектора. Линейные операции над
векторами в координатной форме
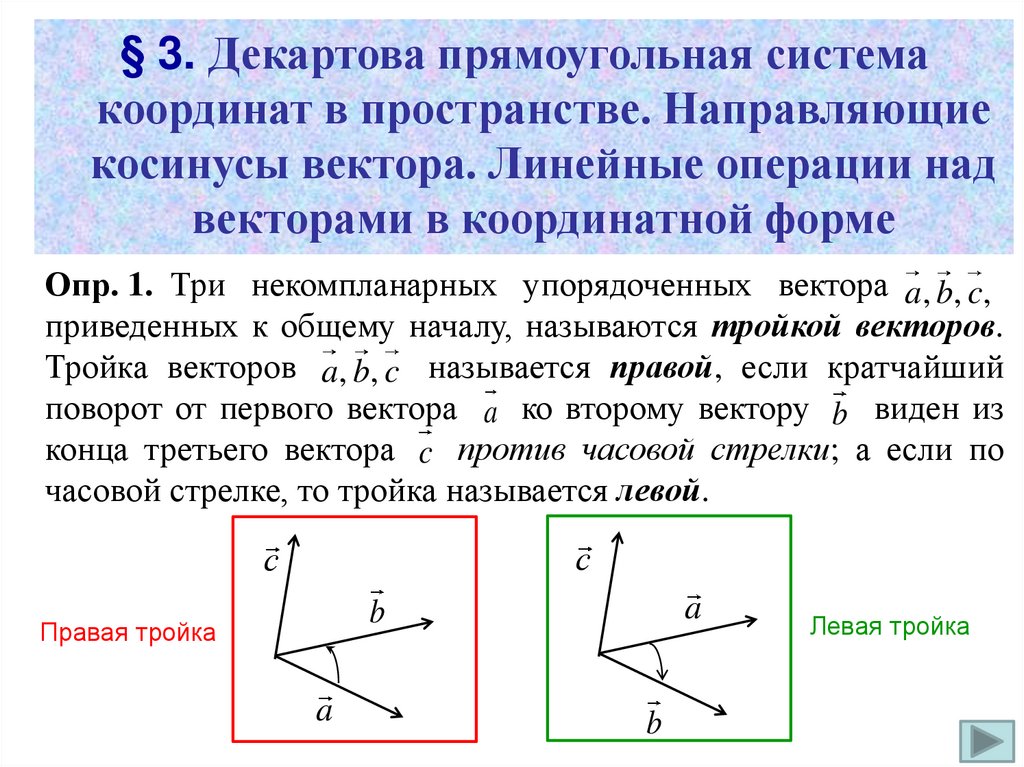
Опр. 1. Три некомпланарных упорядоченных вектора a, b, c,
приведенных к общему началу, называются тройкой векторов.
Тройка векторов a, b, c называется правой, если кратчайший
поворот от первого вектора a ко второму вектору b виден из
конца третьего вектора c против часовой стрелки; а если по
часовой стрелке, то тройка называется левой.
с
с
a
b
Правая тройка
a
b
Левая тройка

24.

Опр.
2.
Базис
в
пространстве
называется
ортонормированным, если все образующие его векторы имеют
единичную длину и попарно перпендикулярны (ортогональны).
Опр. 3. Правая декартова прямоугольная система
координат в пространстве определяется точкой O – началом
координат и ортонормированным базисом
i; j; k , векторы
которого образуют правую тройку. Оси координат Ox, Oy, Oz
сонаправлены соответственно с векторами i, j , k , которые
называются ортами.

25.

Декартовы координаты вектора
Пусть в пространстве задана прямоугольная декартова система
координат Oxyz.
Так как орты i, j , k образуют базис, то а xi y j zk .
Вектор OM называется радиус-вектором точки М.
OM 1 прi OM i;
OM 2 пр j OM j;
OM 3 пр k OM k
a OM OM 1 OM 2 OM 3 прi OM i пр j OM j пр k OM k .
z
M3
k
M1
x
i
а
O j
M
M2
y
Следовательно, координаты
а в
вектора
декартовой
прямоугольной
системе
координат равны проекциям
этого
вектора
на
оси
координат:
x прOx a; y прOy a; z прOz a.

26.

Координаты
радиус-вектора OM называются
также
координатами точки М, при этом координата x называется
абсциссой, y – ординатой, z – аппликатой.
Диагональ параллелепипеда:
2
2
2
2
OM OM 1 OM 2 OM 3 x 2 y 2 z 2 .
z
Следовательно, длина вектора
a xi yj zk равна
корню из
суммы
квадратов
его
декартовых координат:
M3
а
k
O
M1
x
i
j
M
M2
y
a x2 y 2 z 2 .

27.

Направляющие косинусы вектора
Вектор (свободный вектор) полностью характеризуется своей
длиной и направлением.
Косинусы этих углов cos , cos , cos называются направляющими
косинусами вектора а.
z
a x; y; z , т.е. a xi y j zk .
x a cos ; y a cos ; z a cos ,
cos
x
a
; cos
y
a
; cos
z
.
a
x
Основное свойство направляющих косинусов:
а
O
β
y
cos2 cos2 cos2 1.
Вектор ea cos ; cos ; cos называется ортом или единичным
вектором направления вектора а , поскольку он сонаправлен с
вектором а и имеет длину, равную 1. Заметим, что e а .
a
а

28.

Пример 1. Проверим, может ли вектор образовывать с
координатными осями углы:
а) 45 ; 135 ; 30 ;
б) 45 ; 60 ; 120 .
а) cos 2 cos 2 cos 2 cos 45 cos 135 cos 30
2
1 1 3
1,
2 2 4
2
2
Не может.
б) cos 2 cos 2 cos 2 cos 2 45 cos 2 60 cos 2 120
1 1 1
1,
2 4 4
Такой вектор существует.

29.

Линейные операции над векторами в координатной форме
a xa ; ya ; za ;
b xb ; yb ; zb ,
т. е.
a xa i ya j za k ;
b xb i yb j zb k .
a b ( xa i ya j za k ) ( xb i yb j zb k )
( xa xb )i ( ya yb ) j ( za zb )k ;
a ( xa i ya j za k ) xa i ya j za k ,
т. е. линейные операции над векторами сводятся к аналогичным
операциям над их координатами:
a b xa xb ; ya yb ; za zb ;
a xa ; ya ; za .

30.

Условие коллинеарности двух векторов в
координатной форме
a xa ; ya ; za ;
b xb ; yb ; zb .
Тогда
a b a b
xa ya za
,
xb yb zb
т. е. координаты коллинеарных векторов пропорциональны.

31.

Координаты вектора, заданного координатами
начала и конца
Если известны координаты
начала
и
конца
вектора:
A(x1; y1; z1) и B(x2; y2; z2), то
z
A
O
x
B
y
AB OB OA
x2 x1; y2 y1; z2 z1 ,
т. е. для того чтобы найти координаты вектора, нужно от
координат конца вектора отнять соответствующие
координаты начала вектора.

32.

Деление отрезка в данном соотношении
Зная координаты точек A(x1; y1; z1) и
A
B(x2; y2; z2), определить координаты точки
C(xC; yC; zC), которая делит отрезок АВ в
AC
заданном отношении λ, считая от точки А, т. е.
.
AC CB
AC CB.
C
CB
AC xC x1; yC y1; zC z1 ; CB x2 xC ; y2 yC ; z2 zC .
xC x1 ( x2 xC ),
yC y1 ( y2 yC ),
z z ( z z ),
2
C
C 1
x1 x2
y1 y2
z1 + z2
xC
; yC
; zC
.
1
1
1+
В частности, координаты середины отрезка:
x x2
y y2
z + z2
xC 1
; yC 1
; zC 1
.
2
2
2
B

33.

Пример 2. Даны координаты вершин треугольника
A(3; –2; 6), B(2; 3; –1), C(0; 1; 5). Найдем длину медианы АМ.
B
2 0 3 1 1 5
M
;
;
, или M(1; 2; 2).
2
2
2
AM 1 3; 2 ( 2); 2 6 2; 4; 4 .
AM ( 2)2 42 ( 4)2 36 6.
M
А
C

34.

Пример 3. Найдем длины диагоналей параллелограмма,
построенного на векторах a 1;1;1 и b 3i 2 j k .
d1 a b, d 2 a b
d 2 d1
b
d1 a b 1;1;1 3; 2;1
a
1 3;1 2 ;1 1 2; 1; 2 ;
d 2 a b 1;1;1 3; 2;1 1 3;1 2 ;1 1 4; 3; 0 .
d1 2 1 2 9 3;
2
2
2
d2
2
2
4
3
0
25 5.
2

35.

Пример 4. Даны точки A(2; –1; 3), B(–2; 2; 3), C(–4; –1; 1),
D(4; –7; 1). Покажем, что четырехугольник АBCD – трапеция.
B
A
AB 2 2; 2 1; 3 3 4; 3; 0 ;
BC 4 2; 1 2;1 3 2; 3; 2 ;
DC 4 4; 1 7;1 1 8; 6; 0 .
AD 4 2; 7 1;1 3 2; 6; 2 ;
D
AD и BC
2 6 2
,
AD и BC.
не параллельны.
2 3 2
4 3 0
Стороны AB и DC
.
AB и DC
8 6 0
параллельны.
C
Четырехугольник
АBCD – трапеция.
Пример 5. Найдем единичный вектор направления вектора AB,
если A(1; –2; 3), B(3; –4; 4).
eAB
AB
AB
.
AB 3 1; 4 2; 4 3 2; 2;1 ;
AB 2 2 12 9 3,
2
2
2 2 1
eAB ; ; .
3 3 3