Векторная алгебра

1. Векторная алгебра

Основные понятия
Проекция вектора на ось
Векторный базис на плоскости и в пространстве
Декартова прямоугольная система координат
Действия над векторами, заданными
координатами

2. Основные понятия

Вектором называется направленный отрезок.
Вектор с началом в точке А и концом в точке В обозначается
символом AB или одной буквой a
Длина отрезка AB называется длиной или
модулем вектора и обозначается AB , a
В
a
А
Вектор, длина которого равна нулю, называется нулевым
вектором и обозначается 0 .
Вектор, длина которого равна единице, называется единичным
вектором и обозначается через e .
Единичный вектор, направление которого совпадает с
направлением вектора a , называется ортом вектора и
0
обозначается a .

3. Основные понятия

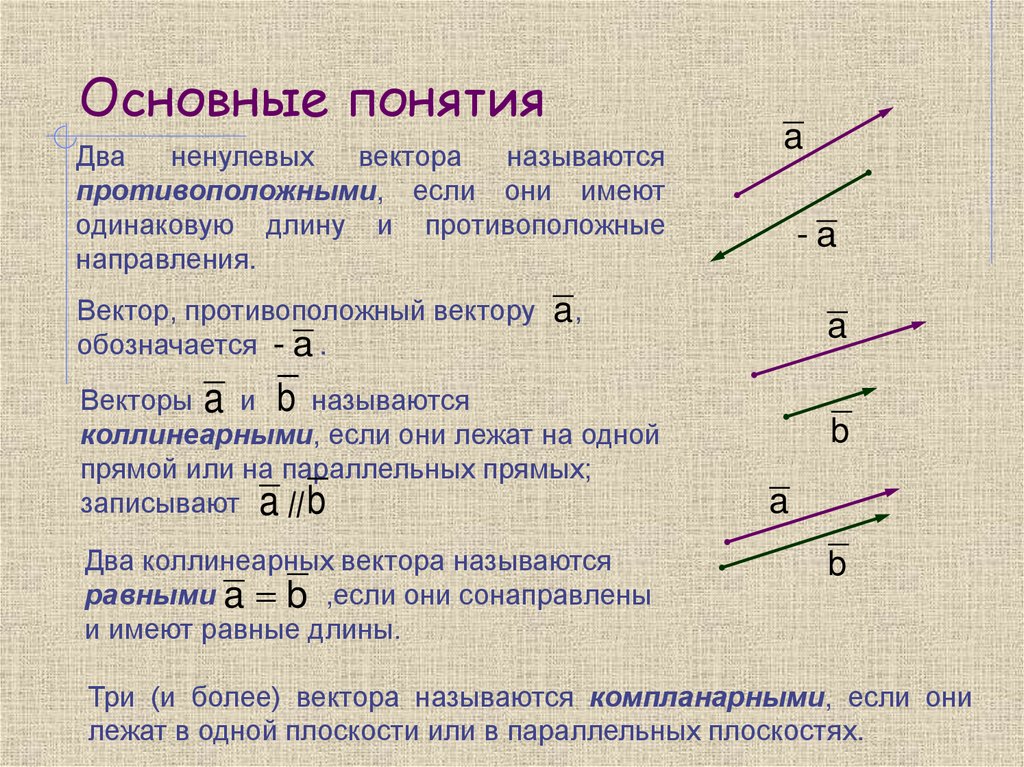
Два
ненулевых
вектора
называются
противоположными, если они имеют
одинаковую длину и противоположные
направления.
a
-a
Вектор, противоположный вектору a ,
обозначается - a .
Векторы a и b называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых;
записывают a || b
Два коллинеарных вектора называются
равными a b ,если они сонаправлены
и имеют равные длины.
a
b
a
b
Три (и более) вектора называются компланарными, если они
лежат в одной плоскости или в параллельных плоскостях.

4. Основные понятия

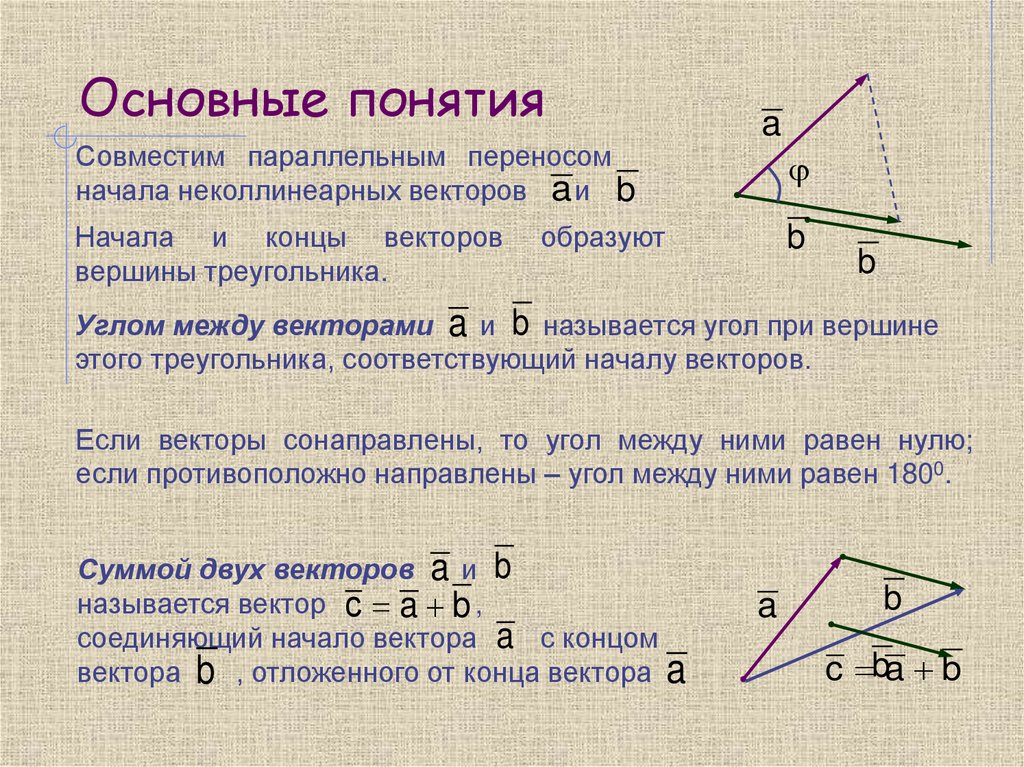
Совместим параллельным переносом
начала неколлинеарных векторов a и b
Начала и концы векторов
вершины треугольника.
a
образуют
b
b
Углом между векторами a и b называется угол при вершине
этого треугольника, соответствующий началу векторов.
Если векторы сонаправлены, то угол между ними равен нулю;
если противоположно направлены – угол между ними равен 1800.
Суммой двух векторов a и b
называется вектор с a b ,
соединяющий начало вектора a с концом
вектора b , отложенного от конца вектора a
a
b
c ba b

5. Основные понятия

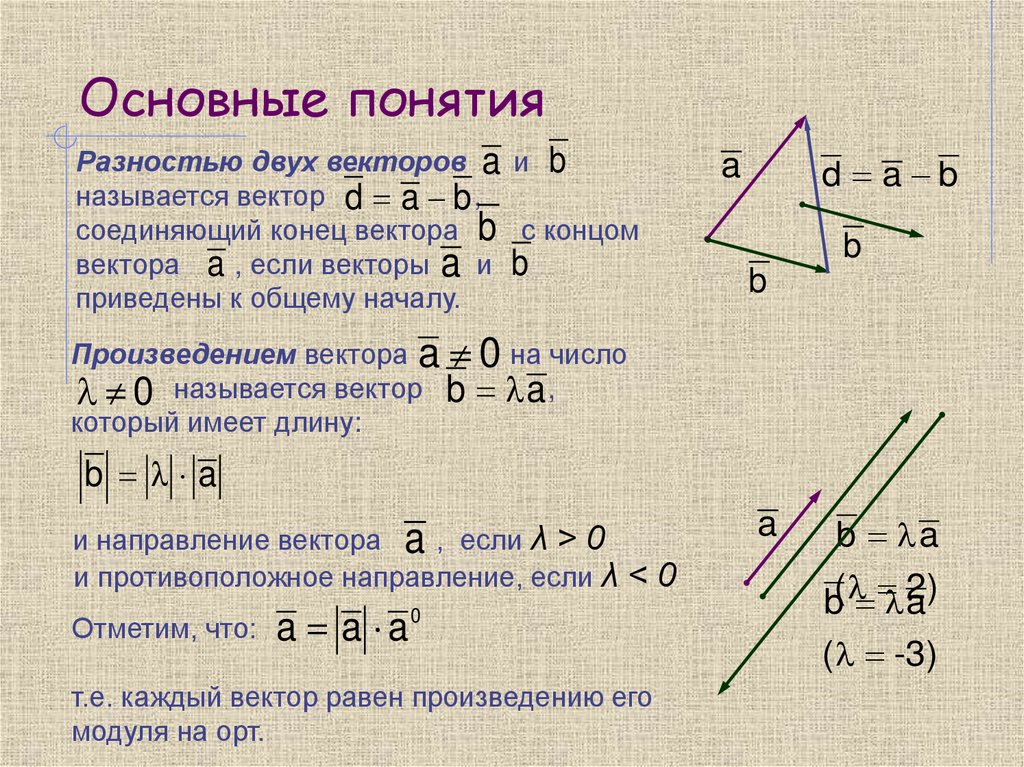
Разностью двух векторов a и b
называется вектор d a b ,
соединяющий конец вектора b с концом
вектора a , если векторы a и b
приведены к общему началу.
a
d a b
b
b
Произведением вектора a 0 на число
0 называется вектор b a ,
который имеет длину:
b a
и направление вектора a , если λ > 0
и противоположное направление, если λ < 0
Отметим, что: a a a
0
т.е. каждый вектор равен произведению его
модуля на орт.
a
b a
2)
b( a
( -3)

6. Основные понятия

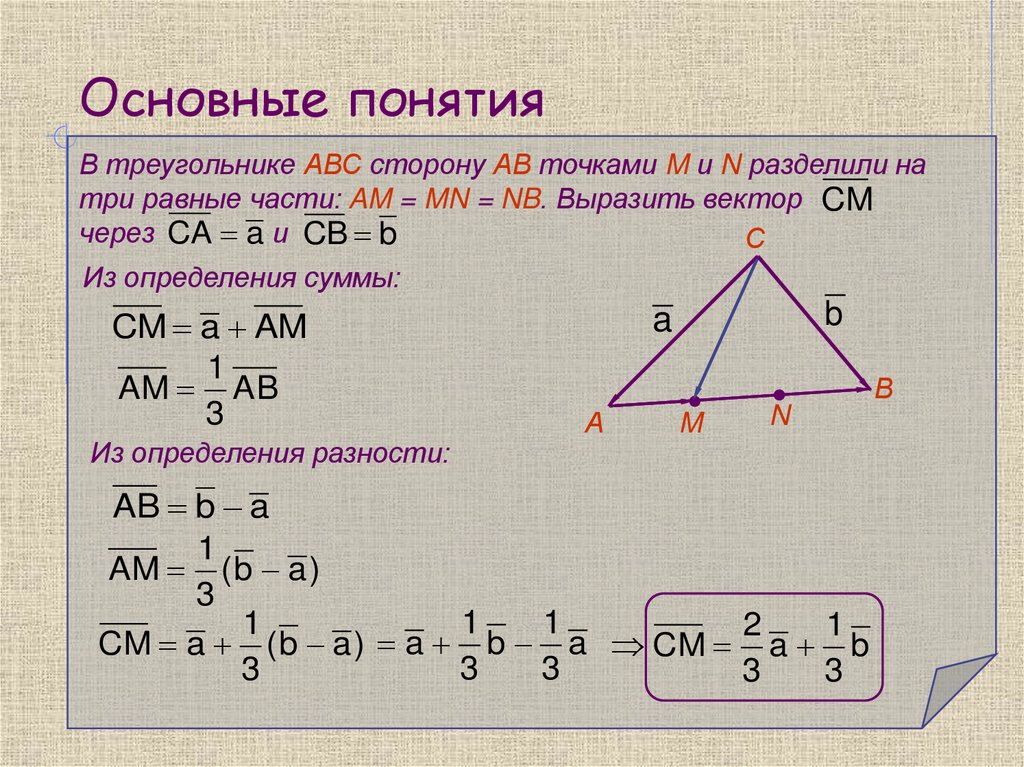
В треугольнике АВС сторону АВ точками M и N разделили на
три равные части: AM = MN = NB. Выразить вектор CM
через CA a и CB b
С
Из определения суммы:
CM a AM
1
AM AB
3
Из определения разности:
b
a
В
А
M
N
AB b a
1
AM ( b a )
3
1
1
1
2
1
CM a ( b a ) a b a CM a b
3
3
3
3
3

7. Проекция вектора на ось

Векторной проекцией вектора AB на ось (направленную
прямую) L называется вектор A B , началом и концом которого
являются соответственно проекции точек А и B на данную ось.
Проекция считается положительной, если вектор A B направлен
так же как и ось L и отрицательной, если в противоположную
сторону
В
В
А
А’
А
В’
L
В’
А’
L
Скалярной проекцией вектора AB на ось L называется скаляр,
абсолютная величина которого равна модулю векторной проекции
того же вектора на ту же ось.
ПРL AB A B

8. Проекция вектора на ось

Свойства скалярных проекций:
1) ПРL AB AB cos
В
В
А
А
А’
В’
В’
3) ПР AB CD EF ПР AB ПР CD ПР EF
2) ПРL AB ПРL AB
L
L
L
L
А’
L
L
о
a ; b ; c - единичные векторы, составляющие с осью L углы 60 ;
о
о
120 ; 180 соответственно
Найти проекцию на ось L вектора d 3a 2 b c
ПРL d ПРL 3a 2b c
3ПР a 2ПР b ПР c
L
L
3 a cos 60o 2 b cos 120o c cos 180o
3 1 0.5 2 1 ( 0.5) 1 ( 1) 0.5
L

9. Векторный базис на плоскости и в пространстве

Линейной комбинацией векторов a1; a2 ; an называется
любой вектор вида:
a x1 a1 x2 a2 xn an
Заданные векторы называются линейно зависимыми,
если какой-либо из векторов является линейной комбинацией
действительные
числа
– векторы называются линейно
остальных;
в противном
случае
коэффициенты (между
линейной
комбинации,
независимымыми
собой).
которых
хотя бы один
не равен
нулюкомбинации некоторых
Еслииз
вектор
представлен
в виде
линейной
векторов, то говорят, что он разложен по этим векторам.
Так например, если вектор
c xa yb , то можно сказать,
что вектор c разложен по
векторам a и b , а вектора
c ; a ; b - линейно зависимые.
a
b
x a
c xa yb
y b

10. Векторный базис на плоскости и в пространстве

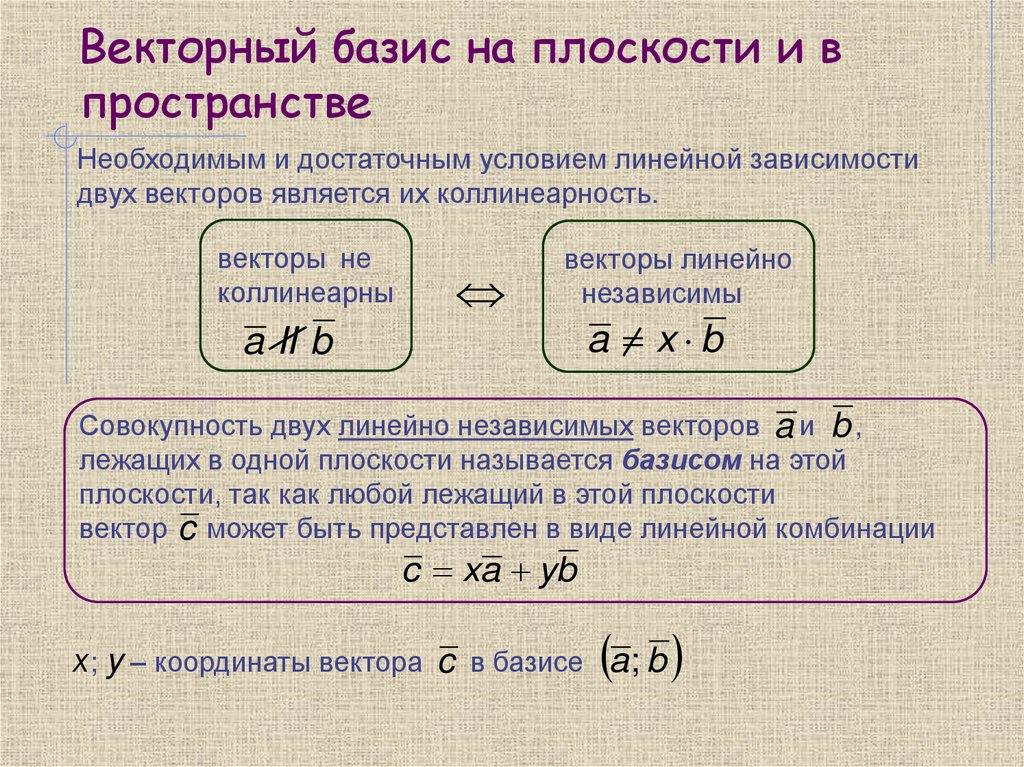
Необходимым и достаточным условием линейной зависимости
двух векторов является их коллинеарность.
векторы не
коллинеарны
векторы линейно
независимы
a II b
a x b
Совокупность двух линейно независимых векторов a и b ,
лежащих в одной плоскости называется базисом на этой
плоскости, так как любой лежащий в этой плоскости
вектор c может быть представлен в виде линейной комбинации
c xa yb
х; y – координаты вектора c в базисе a; b

11. Векторный базис на плоскости и в пространстве

Необходимым и достаточным условием линейной зависимости
трех векторов является их компланарность.
векторы
a; b ; c
не
компланарны
векторы линейно
независимы
c xa yb
Совокупность трех линейно независимых векторов a; b ; c ,
называется базисом в пространстве, так как любой вектор d в
пространстве может быть представлен в виде линейной
комбинации:
d xa yb zc
х; y; z – координаты вектора d в базисе a ; b ; c

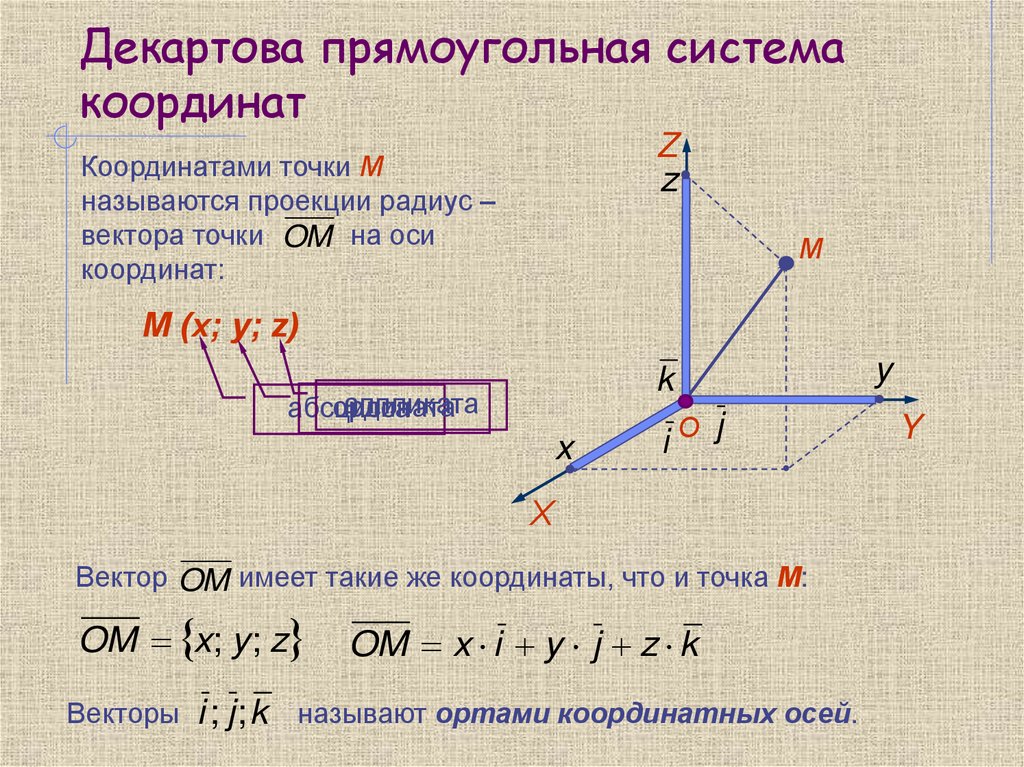
12. Декартова прямоугольная система координат

Векторный базис называется ортонормированным, если он
образован единичными взаимно перпендикулярными векторами.
Базисные векторы обозначаются в этом случае: i ; j ; k
Совокупность фиксированной точки O (начало координат) и
ортонормированного базиса i ; j ; k называется прямоугольной
декартовой системой координат в пространстве.
Прямые Ox, Oy и Oz, проходящие через начало координат в
направлении базисных векторов i ; j ; k называются осями
координат. Оx - ось абсцисс, Оy - ось ординат, Оz - ось аппликат
Плоскости, проходящие через оси координат, называются
координатными плоскостями. Они делят пространство на
восемь областей - октантов.

13. Декартова прямоугольная система координат

Z
z
Координатами точки М
называются проекции радиус –
вектора точки OM на оси
координат:
М
М (x; y; z)
k
аппликата
ордината
абсцисса
x
iО j
Х
Вектор OM имеет такие же координаты, что и точка М:
OM x; y ; z
Векторы i ; j ; k
OM x i y j z k
называют ортами координатных осей.
y
Y

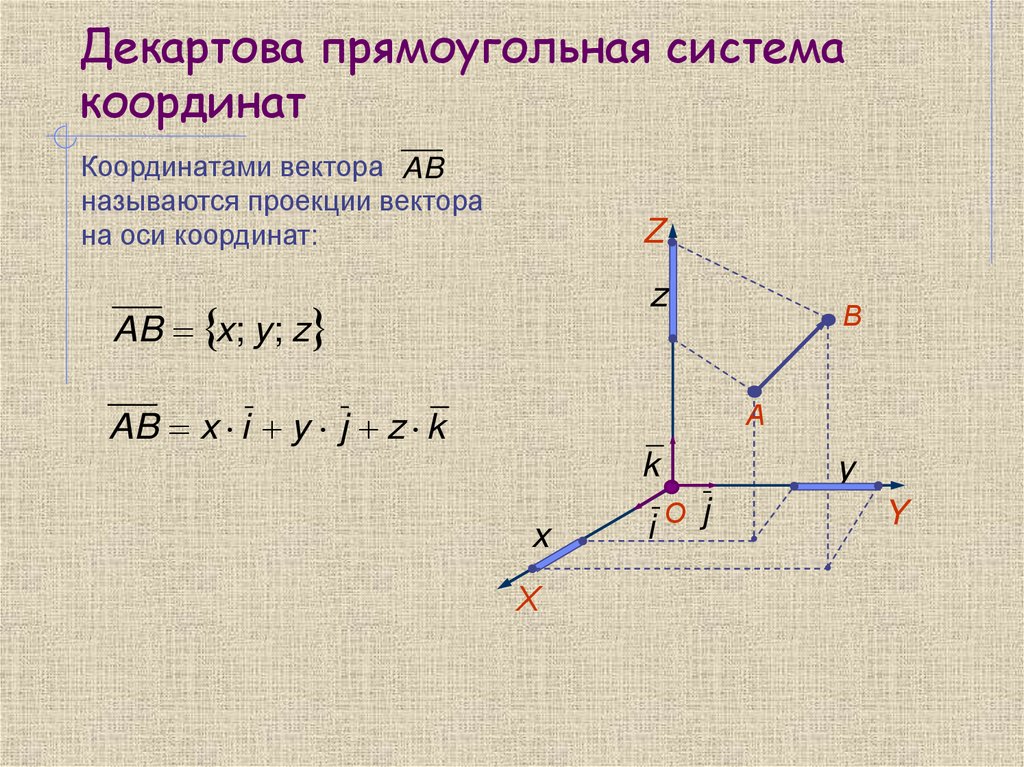
14. Декартова прямоугольная система координат

Координатами вектора AB
называются проекции вектора
на оси координат:
Z
z
AB x; y ; z
В
А
AB x i y j z k
k
x
Х
iО j
y
Y

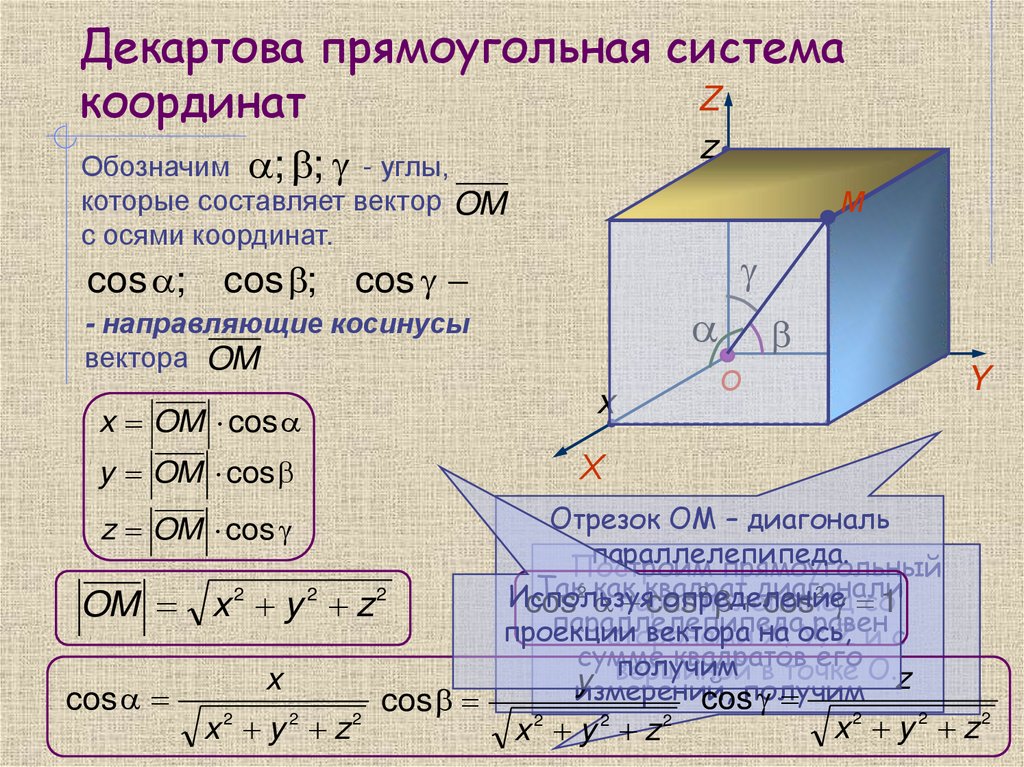
15. Декартова прямоугольная система координат

Декартова прямоугольная система
Z
координат
z
Обозначим ; ; - углы,
которые составляет вектор OM
с осями координат.
cos ;
cos ;
М
cos
- направляющие косинусы
вектора OM
x OM cos
x
y OM cos
Х
y
О
Y
Отрезок ОМ – диагональ
параллелепипеда.
Построим
прямоугольный
Так
как
квадрат
диагонали
2
2
2
2
2
2
Используя
определение
параллелепипед
cos
cos
cos
со1
x y z
параллелепипеда
равен
проекции
вектора на
сторонами
X; ось,
Y; Z и с
сумме
квадратов
его О.
получим в точке
вершиной
z
x
y
измерений,
получим
cos
cos
2
2
2
2
2
z OM cos
OM
cos
x y z
x 2 y 2 z2
x y z2

16. Действия над векторами, заданными координатами

Пусть в декартовой прямоугольной системе координат заданы
векторы:
a x1 i y1 j z1 k
b x2 i y 2 j z2 k
По свойствам скалярной проекции вектора на ось получим:
a b x1 x2 i y1 y 2 j z1 z2 k
a x1 i y1 j z1 k
По координатам точек А(ха; уа; zа ) и В (хb; уb; zb) найти
координаты вектора AB
z
A
AB OB OA
B
OB xb ; y b ; zb OA xa ; y a ; za
AB xb xa ; y b y a ; zb za
o
x
y

17. Действия над векторами, заданными координатами

Найти модуль и орт суммы векторов:
a 3i 5 j 8k
b i j 4k
c a b 3 1 i 5 1 j 8 4 k 2i 4 j 4k
c 22 ( 4)2 4 2 36 6
c c co c o
1
c 2i 4 j 4k
6
o
c
c
1
2
2
i j k
3
3
3

18. Действия над векторами, заданными координатами

Определить , при каких значениях m и n векторы коллинеарны:
a 2; 3; n
b m; 6; 2
Векторы коллинеарны, если существует такое число λ, что
a b
Это векторное равенство должно выполняться для
координат векторов:
2 m
3 ( 6) 0.5; m 4; n 1
n 2