Лекция 6.1 Вектора.Базис-1

1. Векторная алгебра

Основные понятия
Проекция вектора на ось
Векторный базис на плоскости и в пространстве
Декартова прямоугольная система координат
Действия над векторами, заданными
координатами

2. Историческая справка

Термин вектор (от лат.
Vector – « несущий» )
впервые появился в 1845 г.
у ирландского математика
Уильяма Гамильтона (1805 –
1865) в работах по
построению числовых
систем.

3. Основные понятия

Геометрическим
вектором
называется
направленный отрезок.
Вектор с началом в точке А и концом в точке В обозначается
символом AB или одной буквой a
Длина отрезка AB называется длиной или
модулем вектора и обозначается AB , a
В
a
А
Вектор, длина которого равна нулю, называется нулевым
вектором и обозначается 0 .
Вектор, длина которого равна единице, называется единичным
вектором и обозначается через e .
Единичный вектор, направление которого совпадает с
направлением вектора a , называется ортом вектора и
0
обозначается a .

4.

Вектор называется свободным, если его
значение не меняется при произвольном
параллельном переносе.
Свободным вектором является, например,
скорость движения материальной точки. Т.е.
когда заданы направление и длина, но не
фиксируется точка приложения.
Вектор называется скользящим, если его
значение
не
меняется
при
любом
параллельном переносе вдоль линии его
действия.

5.

Примером скользящего вектора может служить
сила, действующая на абсолютно твёрдое
тело (две равные и расположенные на одной
прямой силы оказывают на абсолютно твёрдое
тело одинаковое воздействие).
Вектор
называется
связанным,
фиксировано его начало.
если
Например, сила, приложенная к некоторой
точке упругого тела, представляет собой
связанный вектор.

6.

Свойства свободных векторов изучаются
средствами векторной алгебры (Векторное
исчисление).
Общее понятие вектора, как элемента, так
называемого,
векторного
пространства
определяется аксиоматически.

7.

Векторное исчисление - математическая
дисциплина, в которой изучают свойства
операций над векторами.
При этом понятие вектора представляет
собой
математическую
абстракцию
величин, характеризующихся не только
численным
значением,
но
и
направленностью
(например,
сила,
ускорение, скорость).

8.

Возникновение векторного исчисления тесно
связано с потребностями механики и физики.
До 19 в. для задания векторов использовался
лишь координатный способ, и операции над
векторами сводились к операциям над их
координатами.
Лишь в середине 19 в. усилиями ряда учёных
было создано векторное исчисление, в котором
операции проводились непосредственно над
векторами, без обращения к координатному
способу задания, т.е. геометрически.

9.

Основы векторного исчисления были заложены
исследованиями английского математика У.
Гамильтона и немецкого математика Г.
Грассмана по гиперкомплексным числам (1844
- 50). Их идеи были использованы английским
физиком Дж. К. Максвеллом в его работах по
электричеству и магнетизму.

10.

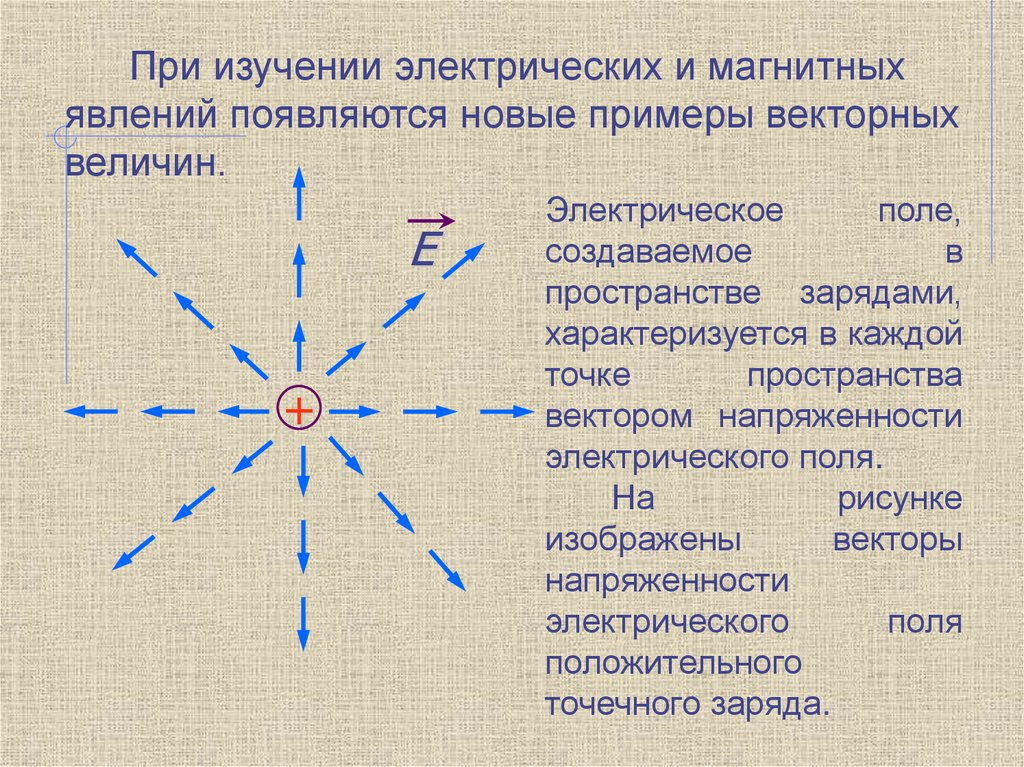
При изучении электрических и магнитных
явлений появляются новые примеры векторных
величин.
E
+
Электрическое
поле,
создаваемое
в
пространстве зарядами,
характеризуется в каждой
точке
пространства
вектором напряженности
электрического поля.
На
рисунке
изображены
векторы
напряженности
электрического
поля
положительного
точечного заряда.

11.

Направление тока
B
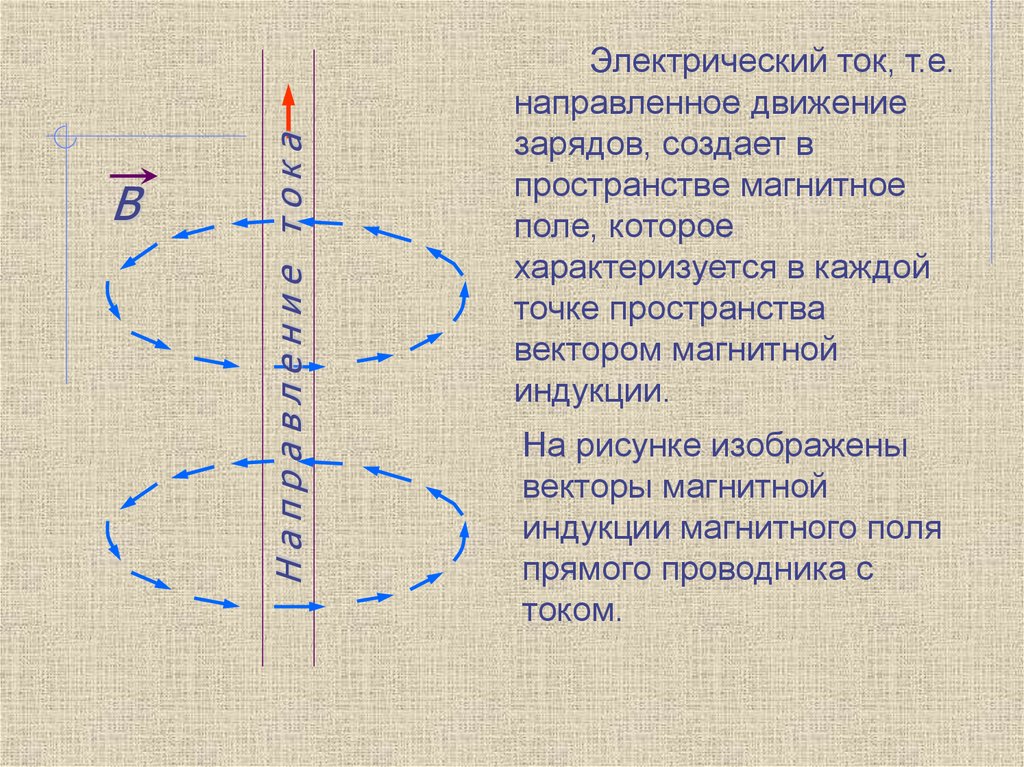
Электрический ток, т.е.
направленное движение
зарядов, создает в
пространстве магнитное
поле, которое
характеризуется в каждой
точке пространства
вектором магнитной
индукции.
На рисунке изображены
векторы магнитной
индукции магнитного поля
прямого проводника с
током.

12.

Современный
вид
векторному
исчислению придал американский физик
Дж. Гиббс.
Значительный
вклад
в
развитие
векторного исчисления внесли русские
учёные.
В первую очередь следует отметить
работы М. В. Остроградского. Им была
доказана основная теорема векторного
анализа (формула Остроградского).

13.

Исследования казанского математика А.
П. Котельникова по развитию винтового
исчисления имели важное значение для
механики и геометрии.
Эти исследования были продолжены
советскими математиками Д. Зейлигером
и А. Широковым. Большое влияние на
развитие Векторного исчисления имела
книга «Векторный анализ», написанная в
1907 русским математиком П. Сомовым.

14. Основные понятия

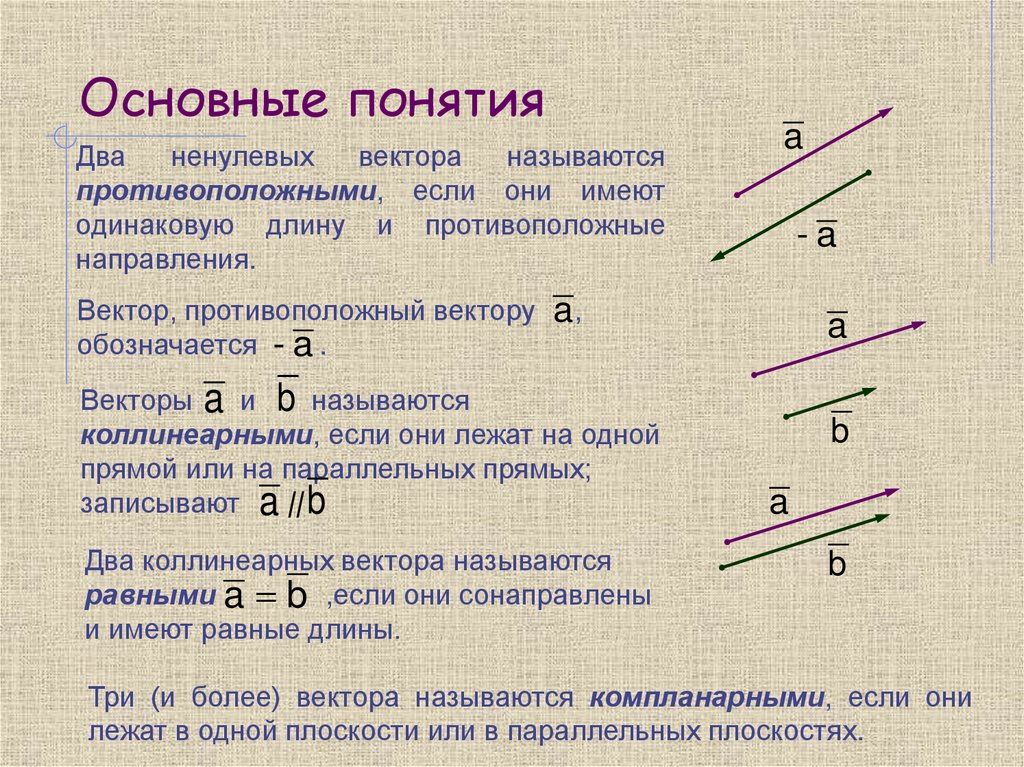
Два
ненулевых
вектора
называются
противоположными, если они имеют
одинаковую длину и противоположные
направления.
a
-a
Вектор, противоположный вектору a ,
обозначается - a .
Векторы a и b называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых;
записывают a || b
Два коллинеарных вектора называются
равными a b ,если они сонаправлены
и имеют равные длины.
a
b
a
b
Три (и более) вектора называются компланарными, если они
лежат в одной плоскости или в параллельных плоскостях.

15. Основные понятия

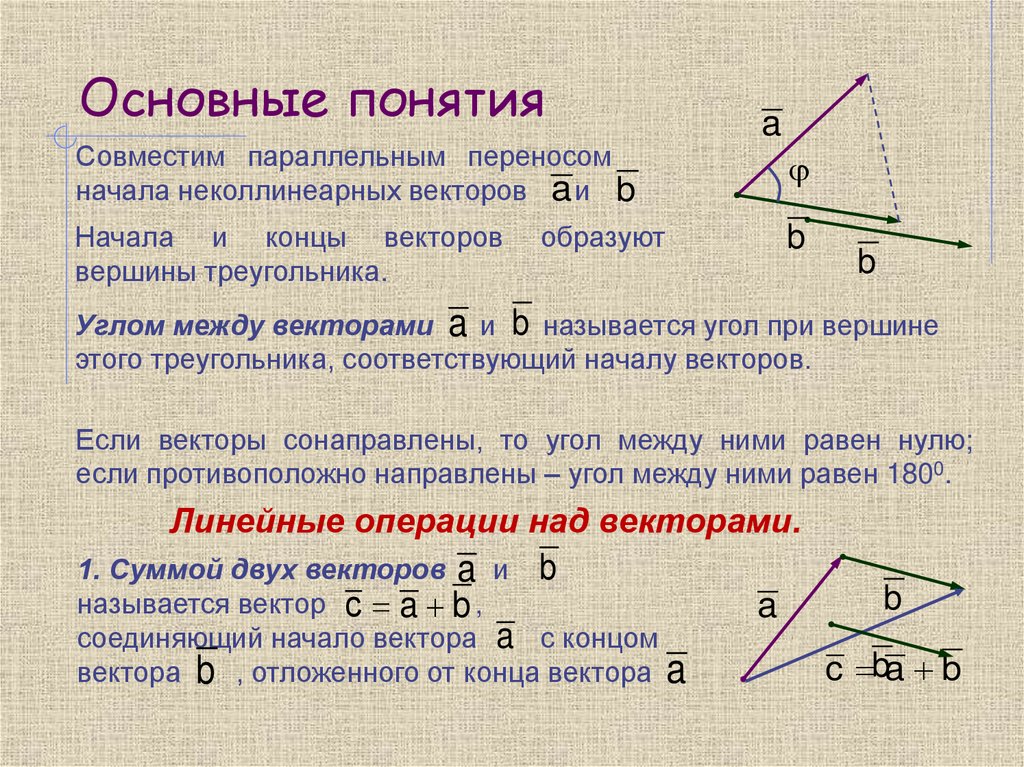
Совместим параллельным переносом
начала неколлинеарных векторов a и b
Начала и концы векторов
вершины треугольника.
a
образуют
b
b
Углом между векторами a и b называется угол при вершине
этого треугольника, соответствующий началу векторов.
Если векторы сонаправлены, то угол между ними равен нулю;
если противоположно направлены – угол между ними равен 1800.
Линейные операции над векторами.
1. Суммой двух векторов a и b
называется вектор с a b ,
соединяющий начало вектора a с концом
вектора b , отложенного от конца вектора a
a
b
c ba b

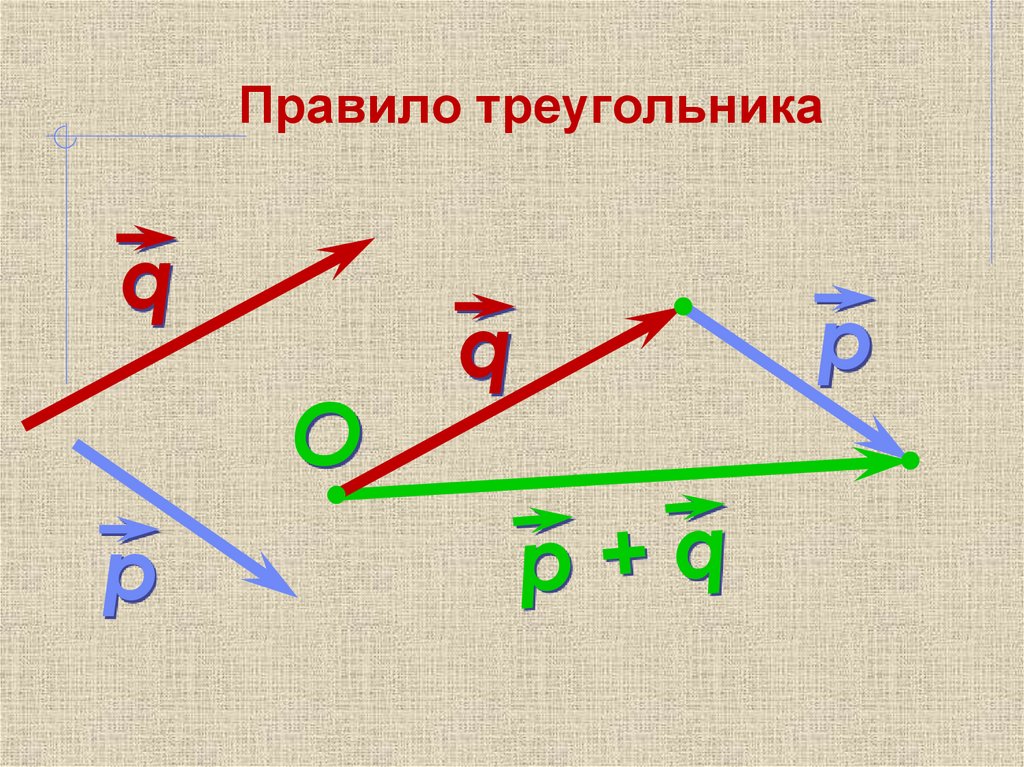
16. Правило треугольника

q
O
р
q
р

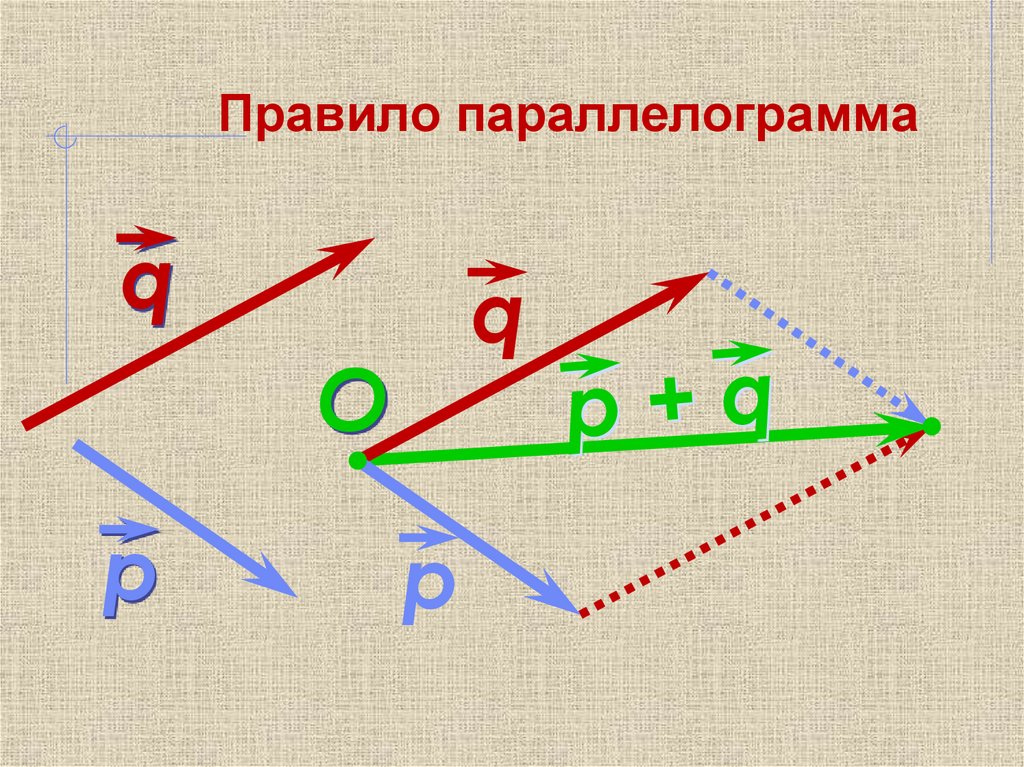
17. Правило параллелограмма

q
q
O
р
р

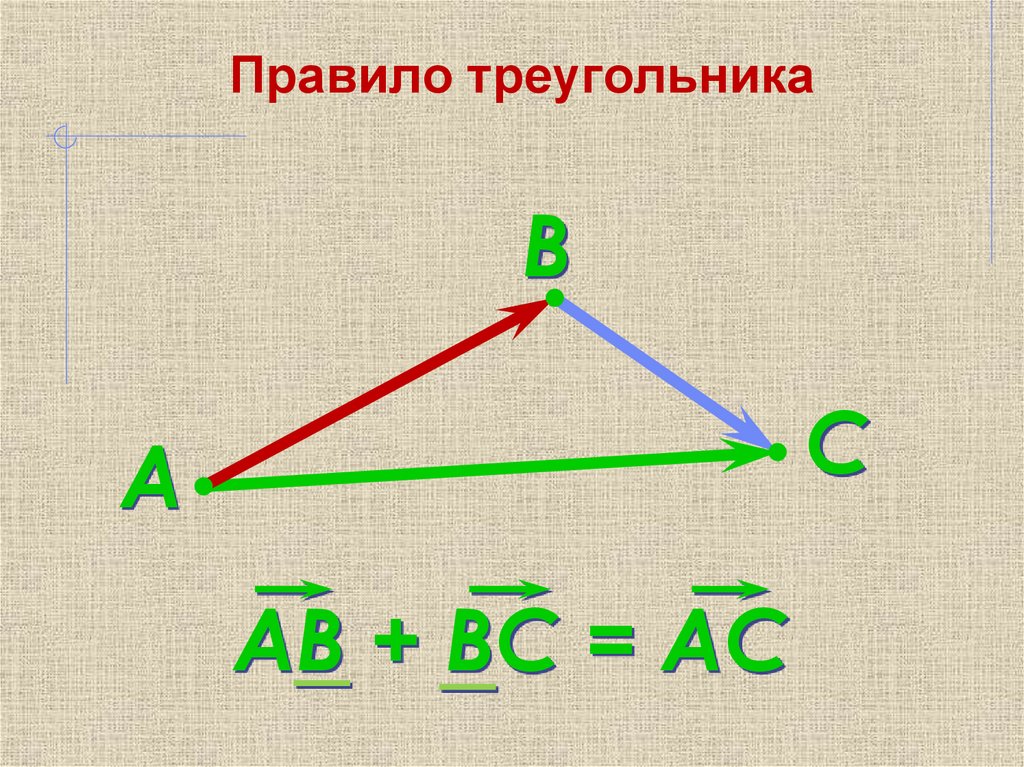
18. Правило треугольника

В
С
А
АВ + ВС = АС

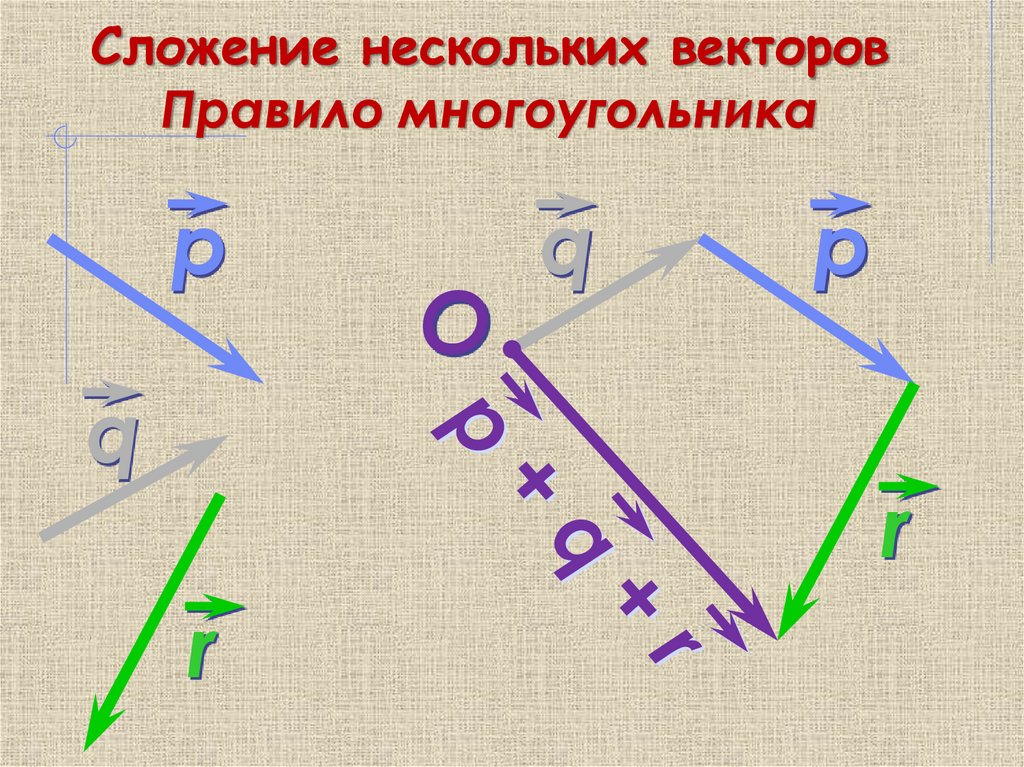
19. Сложение нескольких векторов Правило многоугольника

р
q
O
q
р
r
r

20.

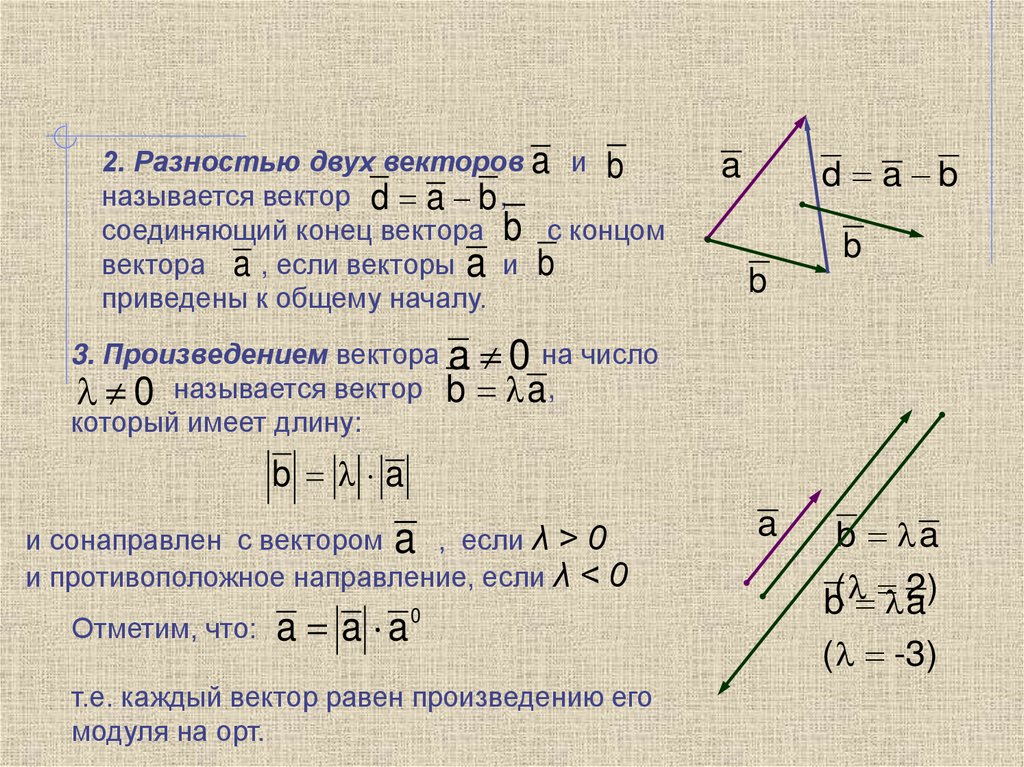
2. Разностью двух векторов a и b
называется вектор d a b ,
соединяющий конец вектора b с концом
вектора a , если векторы a и b
приведены к общему началу.
a
d a b
b
b
3. Произведением вектора a 0 на число
0 называется вектор b a ,
который имеет длину:
b a
и сонаправлен с вектором a , если λ > 0
и противоположное направление, если λ < 0
Отметим, что: a a a
0
т.е. каждый вектор равен произведению его
модуля на орт.
a
b a
2)
b( a
( -3)

21.

Свойства линейных операций над векторами
1) a b b a
2) (a b) c a (b c)
3) a 0 a ;
4) a ( a ) 0 ;
5) ( a ) ( ) a
6) ( ) a a a
7) (a b ) a b
8) 1a a .

22. Основные понятия

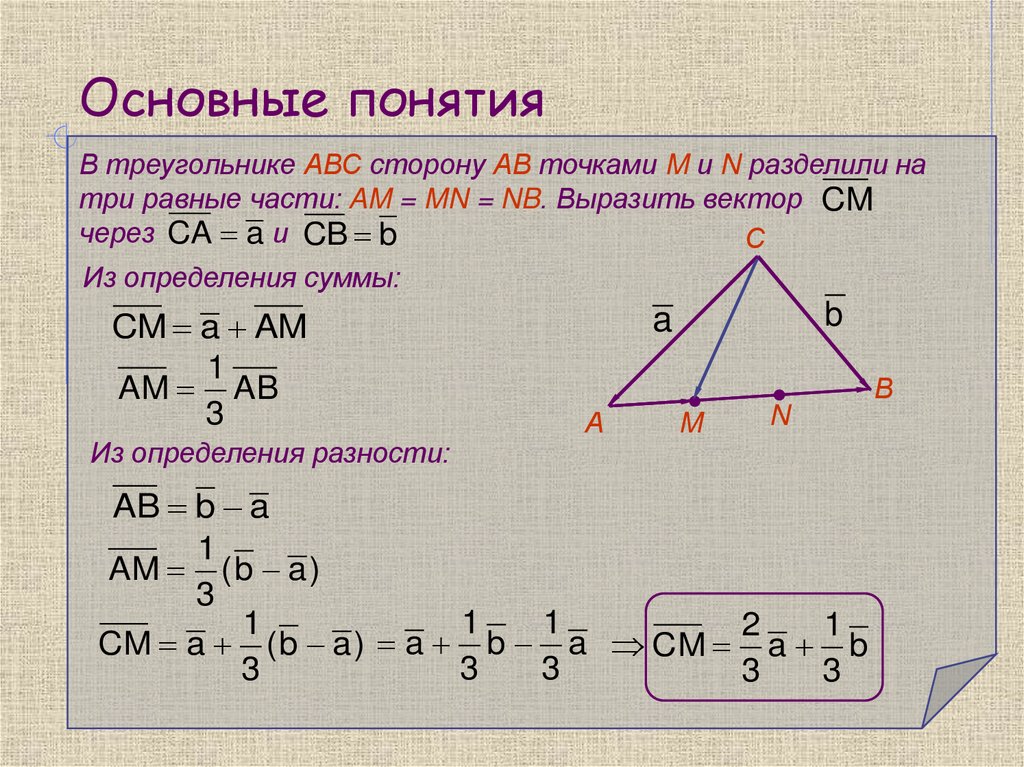
В треугольнике АВС сторону АВ точками M и N разделили на
три равные части: AM = MN = NB. Выразить вектор CM
через CA a и CB b
С
Из определения суммы:
CM a AM
1
AM AB
3
Из определения разности:
b
a
В
А
M
N
AB b a
1
AM ( b a )
3
1
1
1
2
1
CM a ( b a ) a b a CM a b
3
3
3
3
3

23.

Проекция вектора на ось
A
A
O
90
L
O
L
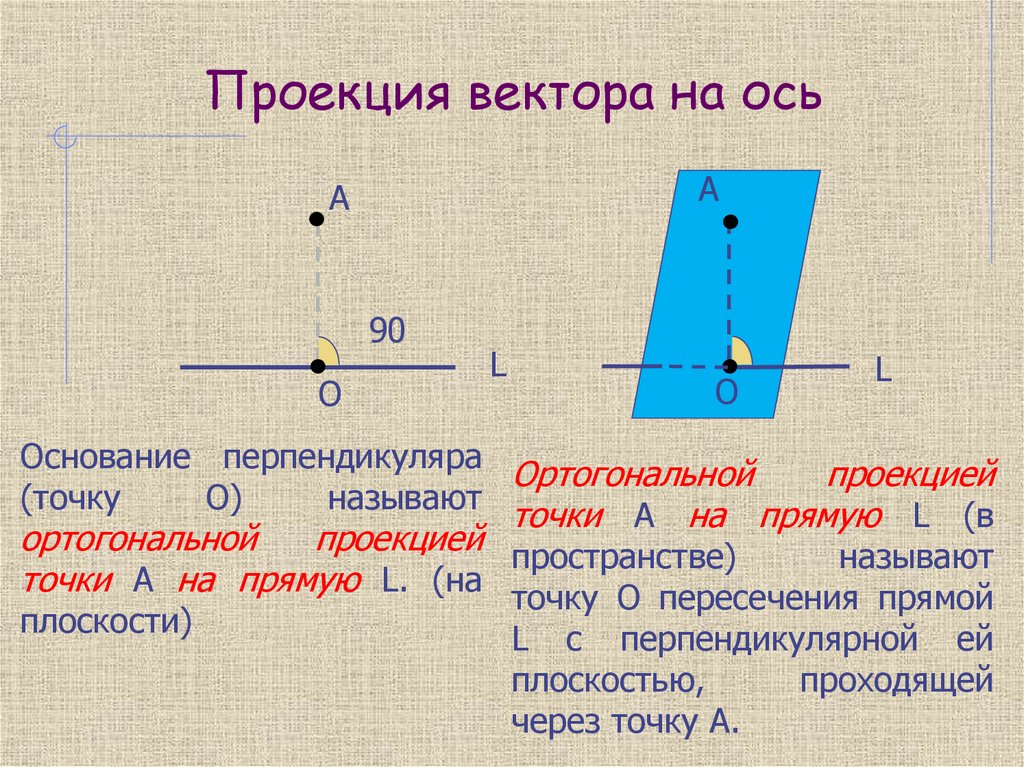
Основание перпендикуляра
Ортогональной
проекцией
(точку
О)
называют
точки А на прямую L (в
ортогональной
проекцией пространстве)
называют
точки А на прямую L. (на точку О пересечения прямой
плоскости)
L с перпендикулярной ей
плоскостью,
проходящей
через точку А.

24.

Ортогональной проекцией вектора AB на прямую L
называется вектор A B , началом и концом которого являются
соответственно ортогональные проекции точек А и B на данную
прямую.
Прямую на которой задано одно из двух возможных направлений
называют осью. Ортогональную проекцию A B вектора AB на
ось можно полностью описать длиной A B
Ортогональная проекция считается положительной, если
вектор A B направлен так же как и ось
и отрицательной, если
в противоположную сторону.
В
В
А
А’
А
В’
L
В’
А’
Ортогональной проекцией вектора AB на ось называется
длина вектора A B со знаком, определяющим направление этого
вектора.
ПР AB A B

25. Проекция вектора на ось

Свойства ортогональных проекций:
В
В
1) ПРL AB AB cos
А
А
А’
В’
В’
3) ПР AB CD EF ПР AB ПР CD ПР EF
2) ПРL AB ПРL AB
L
L
L
L
А’
L
L
о
a ; b ; c - единичные векторы, составляющие с осью L углы 60 ;
о
о
120 ; 180 соответственно
Найти проекцию на ось L вектора d 3a 2 b c
ПРL d ПРL 3a 2b c
3ПР a 2ПР b ПР c
L
L
3 a cos 60o 2 b cos120o c cos180o
3 1 0.5 2 1 ( 0.5) 1 ( 1) 0.5
L

26.

27.

28.

29.

30.

31.

32.

33.

34.

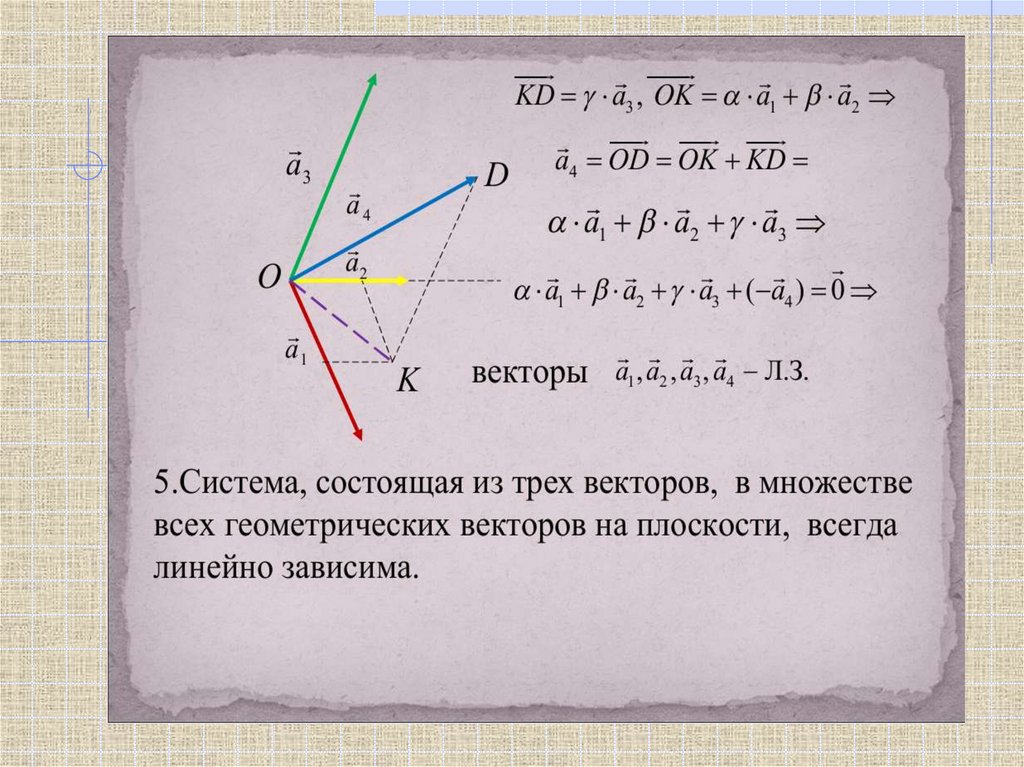
Критерий линейной зависимости
векторов
Для линейной зависимости векторов a1, a2 , ..., an
необходимо и достаточно, чтобы один из них был
линейной комбинацией остальных.
Доказательство.
Необходимость.
Пусть вектора линейно зависимы. Тогда существуют
числа λi, не равные нулю одновременно, такие, что
1 a1 2 a2 ... n an 0.
Пусть λ1 ≠0, тогда
a1 2 a2 ... n an ,
1
1
что доказывает
необходимость.
Достаточность.
Пусть для определенности
a1 2 a2 ... n an .
Тогда ( 1)a a ... a 0, причем 1 2 ... n 0.
1
2 2
n n
Это и есть условие линейной зависимости.

35.

Определение. Базисом некоторой системы векторов
называется
любая
максимальная
линейно
независимая подсистема этой системы векторов.
Иначе говоря e1 , e2 , , en – базис, если
1) e1 , e2 , , en – линейно независимы;
2) e1 , e2 , , en , a – линейно зависимы для любого
вектора a из данной системы векторов.
Базис можно выбрать не единственным образом.
Например, если e1 , e2 , , en – базис, то при 0
e 1 , e2 , , en – также базис.

36.

Теорема 3.4. Любые два базиса данной системы
векторов состоят из одного и того же числа
векторов.
Теорема 3.5. 1) Базисом на плоскости являются
любые два неколлинеарных вектора.
2) Базисом в пространстве являются
любые три некомпланарных вектора.
Теорема 3.6 (о базисе). Каждый вектор линейно
выражается через базис, причем единственным
образом.
e1 , e2 , , en – базис, a – произвольный вектор
a 1 e1 2 e2 n en
При этом 1 , 2 , , n называют координатами
вектора a в базисе e1 , e2 , , en

37.

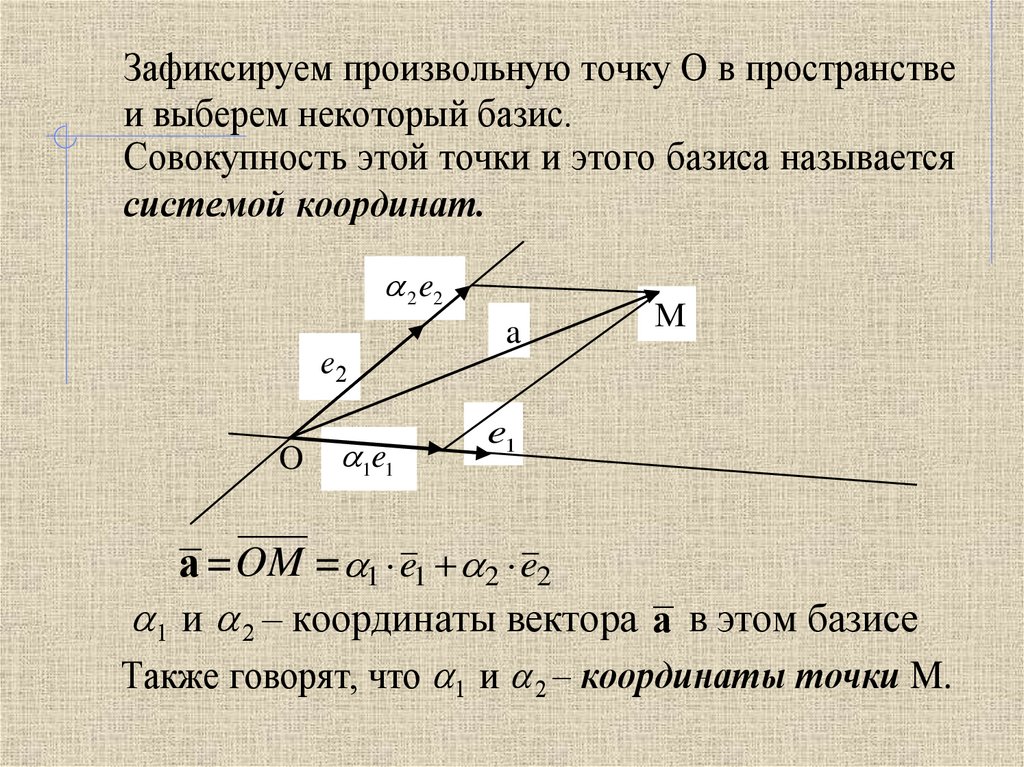
Зафиксируем произвольную точку O в пространстве
и выберем некоторый базис.
Совокупность этой точки и этого базиса называется
системой координат.
2 e2
e2
O
1e1
a
М
e1
a = OM = 1 e1 2 e2
1 и 2 – координаты
e1 2 e2 a в этом базисе
a = OM = 1 вектора
Также говорят, что 1 и 2 – координаты точки M.

38.

Определение
Базис
называется
ортогональным, если образующие его
векторы попарно ортогональны (взаимно
перпендикулярны).
Определение
Ортогональный
базис
называется ортонормированным, если
образующие его векторы имеют единичную
длину.

39. Координаты вектора:

Для записи вектора
x e1 e2 e3
в координатном представлении
используются формы:
x
x ( ; ; )
x
x

40. Векторный базис на плоскости и в пространстве

Линейной комбинацией векторов a1; a2 ; an называется
любой вектор вида:
a x1 a1 x2 a2 xn an
Заданные векторы называются линейно зависимыми,
если какой-либо из векторов является линейной комбинацией
действительные
числа
– векторы называются линейно
остальных;
в противном
случае
коэффициенты (между
линейной
комбинации,
независимымыми
собой).
которых
хотя бы один
не равен
нулюкомбинации некоторых
Еслииз
вектор
представлен
в виде
линейной
векторов, то говорят, что он разложен по этим векторам.
Так например, если вектор
c xa yb , то можно сказать,
что вектор c разложен по
векторам a и b , а вектора
c ; a ; b - линейно зависимые.
a
b
x a
c xa yb
y b

41. Векторный базис на плоскости и в пространстве

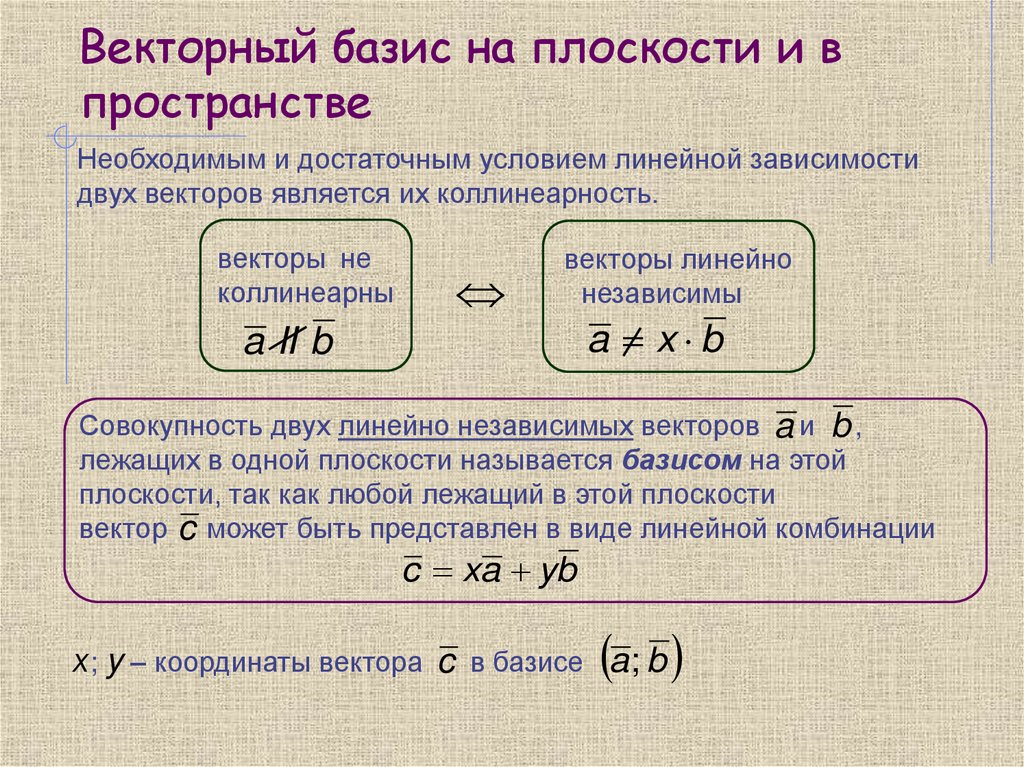
Необходимым и достаточным условием линейной зависимости
двух векторов является их коллинеарность.
векторы не
коллинеарны
векторы линейно
независимы
a II b
a x b
Совокупность двух линейно независимых векторов a и b ,
лежащих в одной плоскости называется базисом на этой
плоскости, так как любой лежащий в этой плоскости
вектор c может быть представлен в виде линейной комбинации
c xa yb
х; y – координаты вектора c в базисе a; b

42. Векторный базис на плоскости и в пространстве

Необходимым и достаточным условием линейной зависимости
трех векторов является их компланарность.
векторы
a; b ; c
не
компланарны
векторы линейно
независимы
c xa yb
Совокупность трех линейно независимых векторов a; b ; c ,
называется базисом в пространстве, так как любой вектор d в
пространстве может быть представлен в виде линейной
комбинации:
d xa yb zc
х; y; z – координаты вектора d в базисе a ; b ; c

43. Декартова прямоугольная система координат

Векторный базис называется ортонормированным, если он
образован единичными взаимно перпендикулярными векторами.
Базисные векторы обозначаются в этом случае: i ; j ; k
Совокупность фиксированной точки O (начало координат) и
ортонормированного базиса i ; j ; k называется прямоугольной
декартовой системой координат в пространстве.
Прямые Ox, Oy и Oz, проходящие через начало координат в
направлении базисных векторов i ; j ; k называются осями
координат. Оx - ось абсцисс, Оy - ось ординат, Оz - ось аппликат
Плоскости, проходящие через оси координат, называются
координатными плоскостями. Они делят пространство на
восемь областей - октантов.

44. Декартова прямоугольная система координат

Z
z
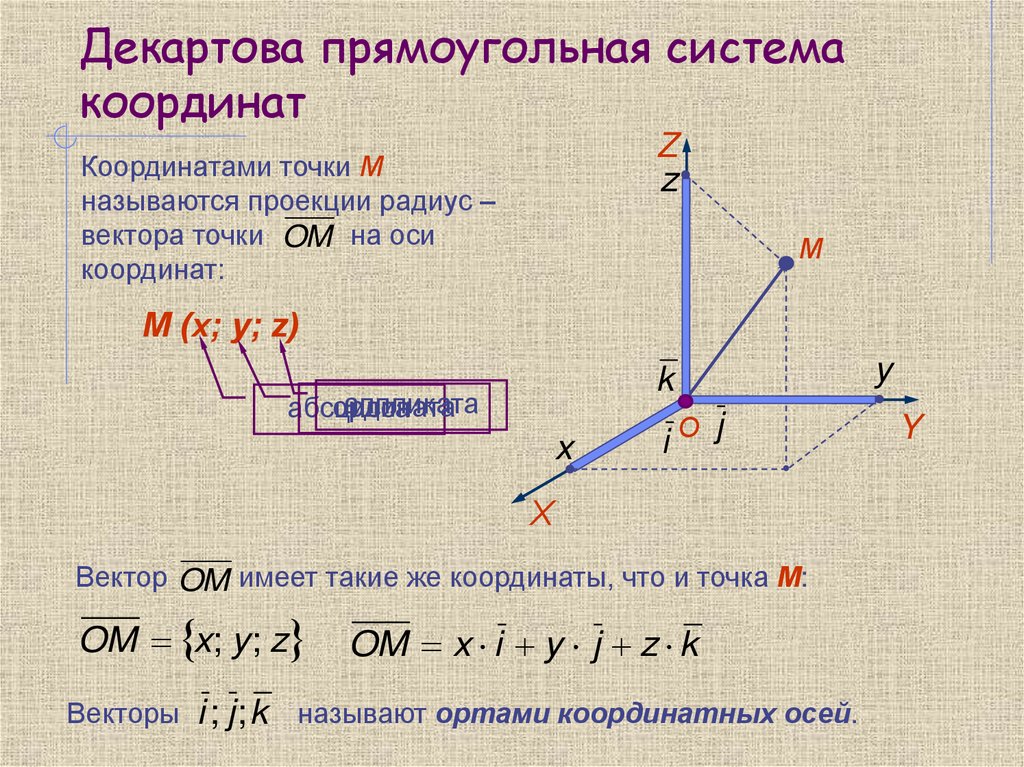
Координатами точки М
называются проекции радиус –
вектора точки OM на оси
координат:
М
М (x; y; z)
k
аппликата
ордината
абсцисса
x
iО j
Х
Вектор OM имеет такие же координаты, что и точка М:
OM x; y ; z
Векторы i ; j ; k
OM x i y j z k
называют ортами координатных осей.
y
Y

45. Декартова прямоугольная система координат

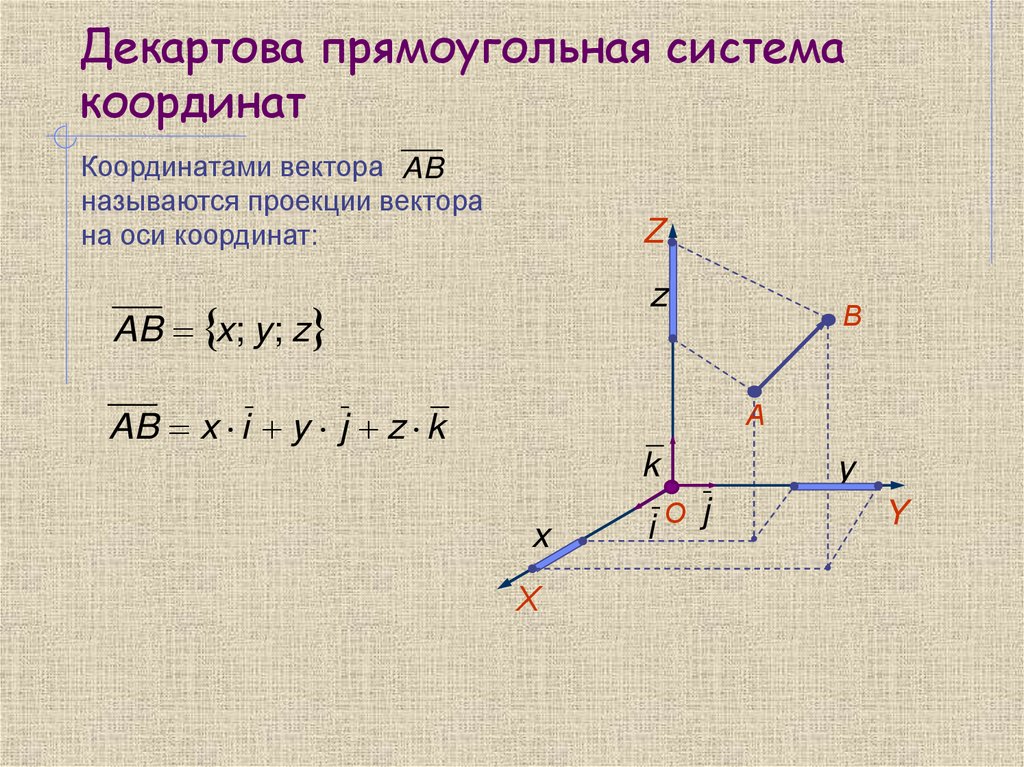
Координатами вектора AB
называются проекции вектора
на оси координат:
Z
z
AB x; y ; z
В
А
AB x i y j z k
k
x
Х
iО j
y
Y

46. Декартова прямоугольная система координат

Декартова прямоугольная система
Z
координат
z
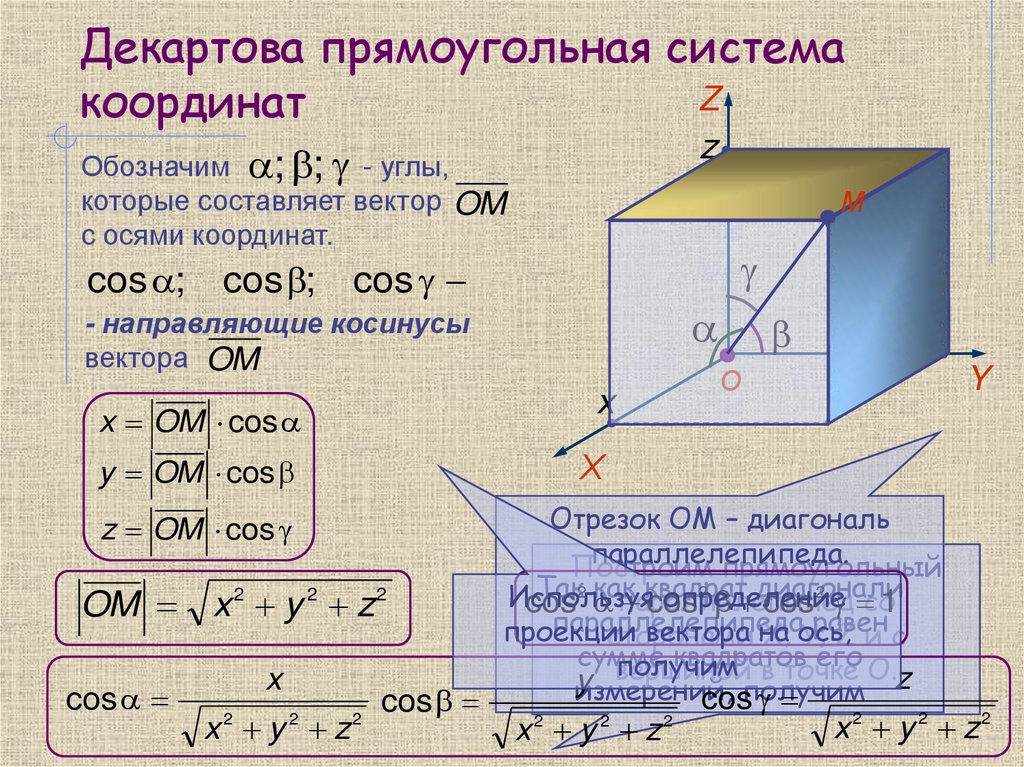
Обозначим ; ; - углы,
которые составляет вектор OM
с осями координат.
cos ;
cos ;
М
cos
- направляющие косинусы
вектора OM
x OM cos
x
y OM cos
Х
y
О
Y
Отрезок ОМ – диагональ
параллелепипеда.
Построим
прямоугольный
Так
как
квадрат
диагонали
2
2
2
2
2
2
Используя
определение
параллелепипед
cos
cos
cos
со1
x y z
параллелепипеда
равен
проекции
вектора на
сторонами
X; ось,
Y; Z и с
сумме
квадратов
его О.
получим в точке
вершиной
z
x
y
измерений,
получим
cos
cos
2
2
2
2
2
z OM cos
OM
cos
x y z
x 2 y 2 z2
x y z2

47. Действия над векторами, заданными координатами

Пусть в декартовой прямоугольной системе координат заданы
векторы:
a x1 i y1 j z1 k
b x2 i y 2 j z2 k
По свойствам скалярной проекции вектора на ось получим:
a b x1 x2 i y1 y 2 j z1 z2 k
a x1 i y1 j z1 k
По координатам точек А(ха; уа; zа ) и В (хb; уb; zb) найти
координаты вектора AB
z
A
AB OB OA
B
OB xb ; y b ; zb OA xa ; y a ; za
AB xb xa ; y b y a ; zb za
o
x
y

48. Действия над векторами, заданными координатами

Найти модуль и орт суммы векторов:
a 3i 5 j 8k
b i j 4k
c a b 3 1 i 5 1 j 8 4 k 2i 4 j 4k
c 22 ( 4)2 4 2 36 6
c c co c o
1
c 2i 4 j 4k
6
o
c
c
1
2
2
i j k
3
3
3

49. Действия над векторами, заданными координатами

Определить , при каких значениях m и n векторы коллинеарны:
a 2; 3; n
b m; 6; 2
Векторы коллинеарны, если существует такое число λ, что
a b
Это векторное равенство должно выполняться для
координат векторов:
2 m
3 ( 6) 0.5; m 4; n 1
n 2

50.

Лемма 4.2 (критерий коллинеарности векторов в
координатной форме). Два ненулевых вектора a и
b коллинеарны тогда и только тогда, когда их
координаты пропорциональны.
Пример
a ={2, 4, 0}
b ={1, 2, 0}
=2
2= 1
4= 2
0= 0
векторы a и b коллинеарны
a x = bx , a y = bx , a z = bx a x
ay
az
=
=
ay
ax
az
bx
bz
by
, =
, =
=
bx
bz
by

51.

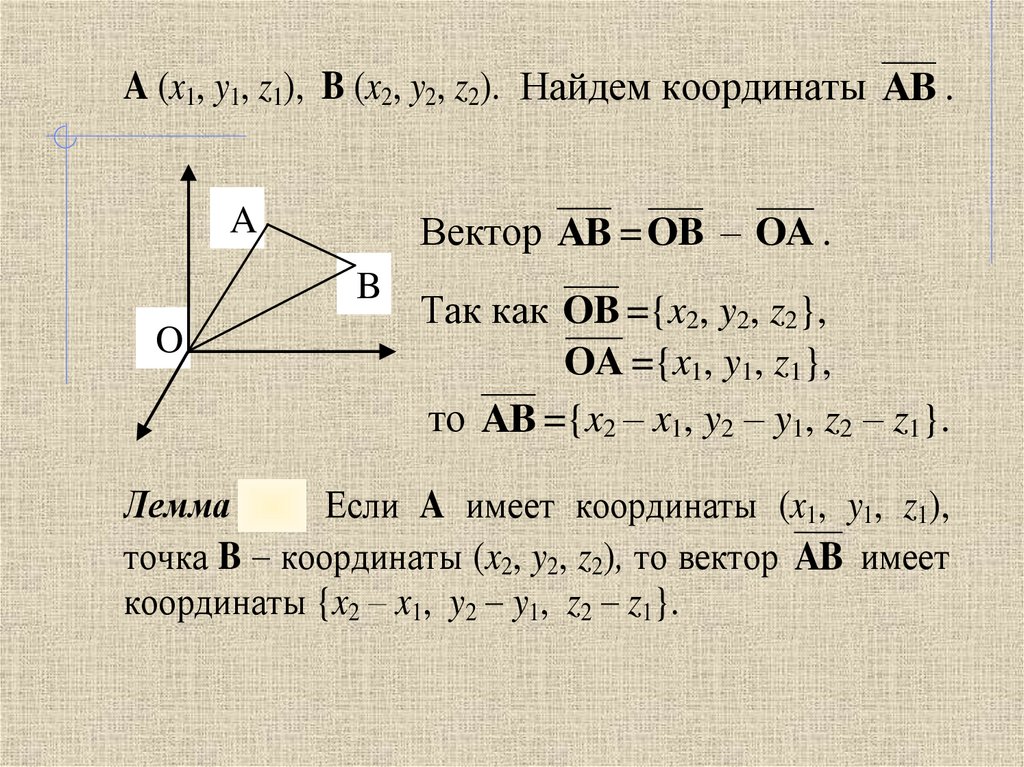
A (x1, y1, z1), B (x2, y2, z2). Найдем координаты AB .
A (x1, y1, z1), B (x2, y2, z2). Найдем координаты AB .
A
O
Вектор AB
OB
B –- O
AB==O
OA
A ..
Вектор
B Так как OB ={x2, y2, z2},
Так как OOBA={x
={x21,,yy21,, zz21},
},
OA2-={x
то AB ={x
x1, y1,2-yy1,1,z1z},
2- z1}.
то AB ={x2 – x1, y2 – y1, z2 – z1}.
Лемма 4.3.
4.3. Если
Если A
A имеет
имеет координаты
координаты (x(x1,1, yy11, , zz11),),
Лемма
точкаточка
B координаты
(x2, (xy22,, yz2,2),z2),тото вектор
имеет
AB имеет
B – координаты
вектор AB
координаты
{x2 –{xx21–, xy12, –y2y1–, yz12, –z2z–1}.z1}.
координаты

52.

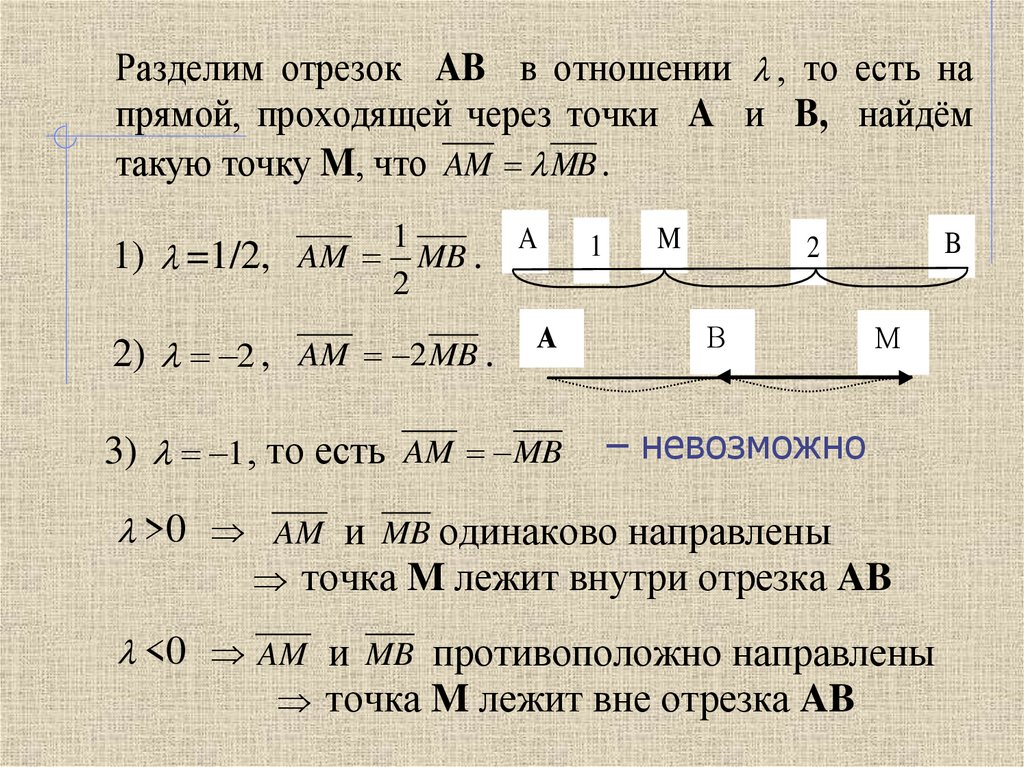
Разделим отрезок AB в отношении , то есть на
прямой, проходящей через точки A и B, найдём
такую точку M, что AM MB .
1
1) =1/2, AM MB .
2
A
2) 2 , AM 2 MB .
А
3) 1 , то есть AM MB
1
M
B
2
В
М
– невозможно
>0 AM и MB одинаково направлены
точка M лежит внутри отрезка AB
<0 AM и MB противоположно направлены
точка M лежит вне отрезка AB

53.

Пусть A (x1, y1, z1), B (x2, y2, z2).
Обозначим координаты точки M (x, y ,z).
Тогда AM ={x–x1, y–y1, z–z1}, MB ={x2–x, y2–y, z2–z}.
Так как AM MB , то
x –x1= (x2–x), y–y1= (y2–y), z–z1= (z2–z).
Откуда получаем, что
x1 x2
y1 y2
z1 z2
x
, y
, z
.
1
1
1

54.

Пример . Даны точки A(1, –1, 2) и B(3, 2, 3).
Найти:Координаты вектора AB :
AB{3 1, 2 ( 1), 3 2} AB{2, 3, 1}.
Найти: Длину вектора
Так какa ax2 a 2y az2 , значитAB 4 9 1 14 .
Найти:Разложение вектора по базису;
Так какa ax i a y j az k , значит AB 2i 3 j k.
Найти: Направляющие косинусы вектора
cos
2
,
14
3
cos
,
14
cos
1
.
14
Найти: Единичный вектор (орт), соответствующий вектору
3 1
0 2
a
Так какa , значит a 14 , 14 , 14 .
a
0