Similar presentations:
Символический метод
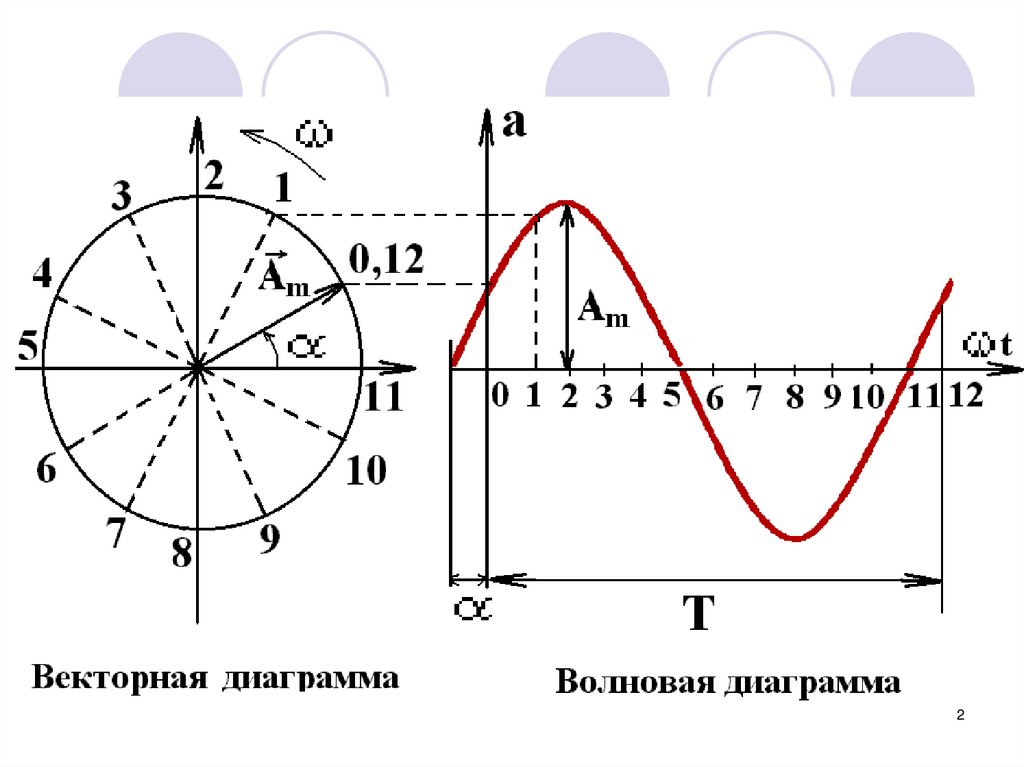
1.
Символический метод1
2.
23.
При токе и напряжении:i I m sin( t )
u U m sin( t )
3
4.
a Am sin( t )A m A m e j A m ;
A m комплексная амплитуда
4
5.
A me j( t ) A m cos( t )jA m sin( t ) - это вращение
A Am / 2 Ae
j
A
А – комплексное действующее значение
или комплексное значение
5
6.
Символический методприменяется для расчета
линейных
цепей с гармоническими токами
и напряжениями
и основан на изображении
синусоид
комплексными числами
6
7.
Следовательно, синусоидальнаявеличина может быть
изображена
вращающимся вектором на
комплексной плоскости, причем
этот вектор записывается в
показательной,
тригонометрической
и алгебраической формах
7
8.
Таким образом:i Im sin( t ) 2 I sin( t )
I Ie
j
I cos jI sin
a jb,
где
j 1
– мнимая единица
8
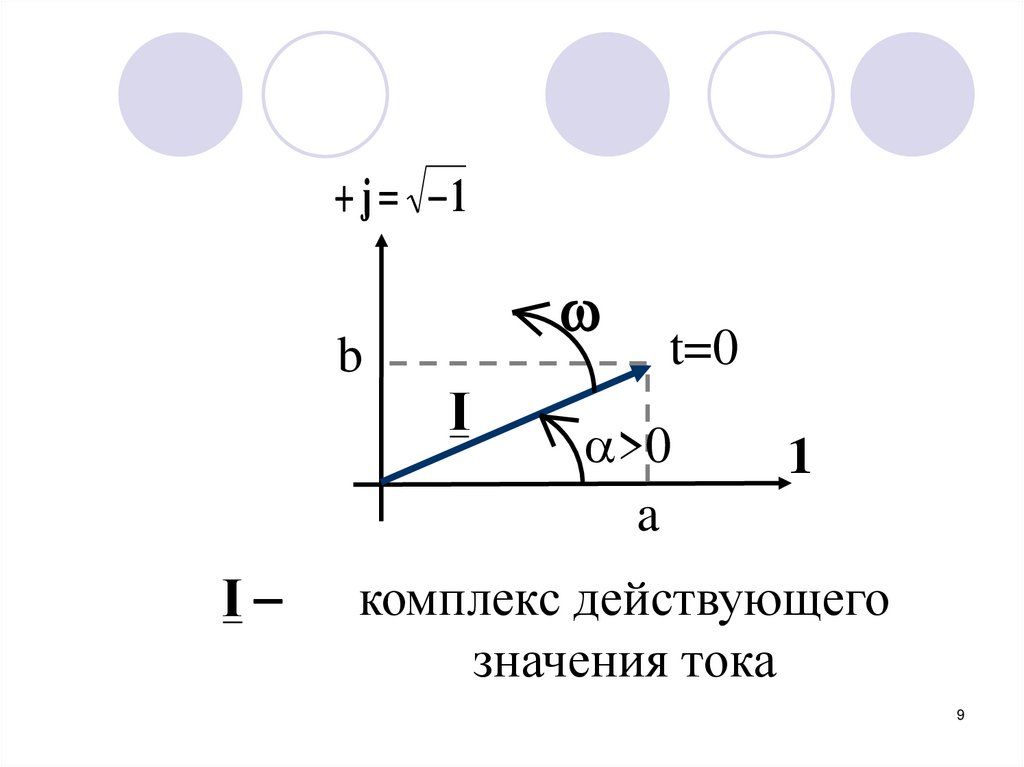
9.
j 1b
I
I
t=0
>0
a
1
комплекс действующего
значения тока
9
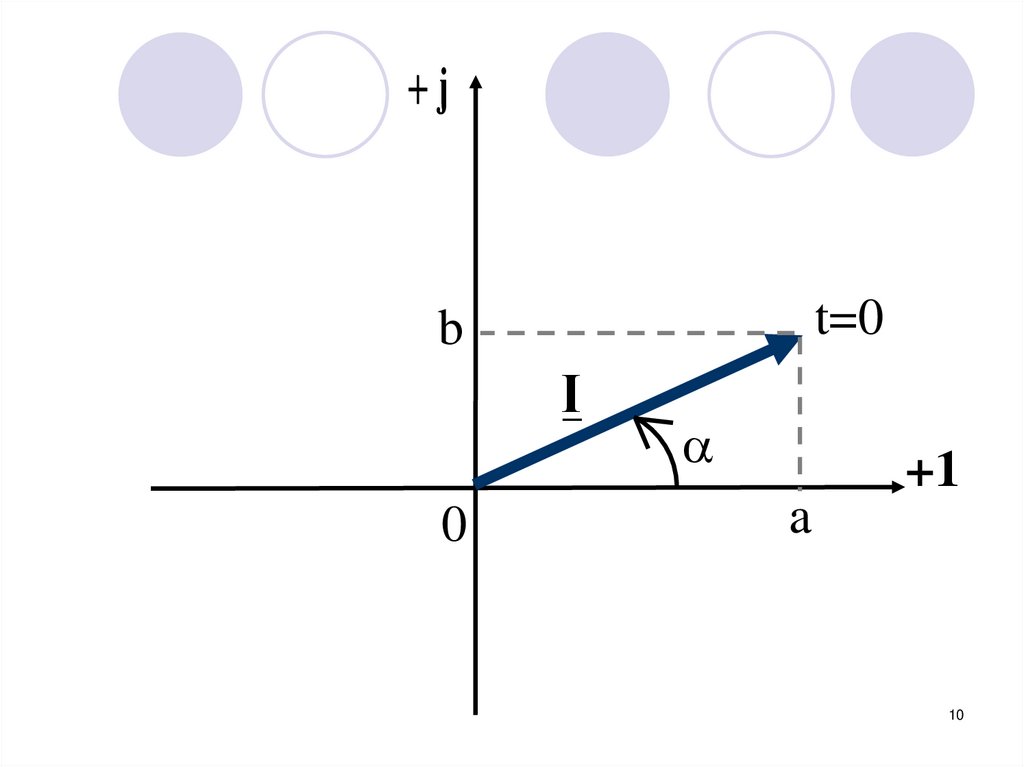
10.
jt=0
b
I
0
+1
a
10
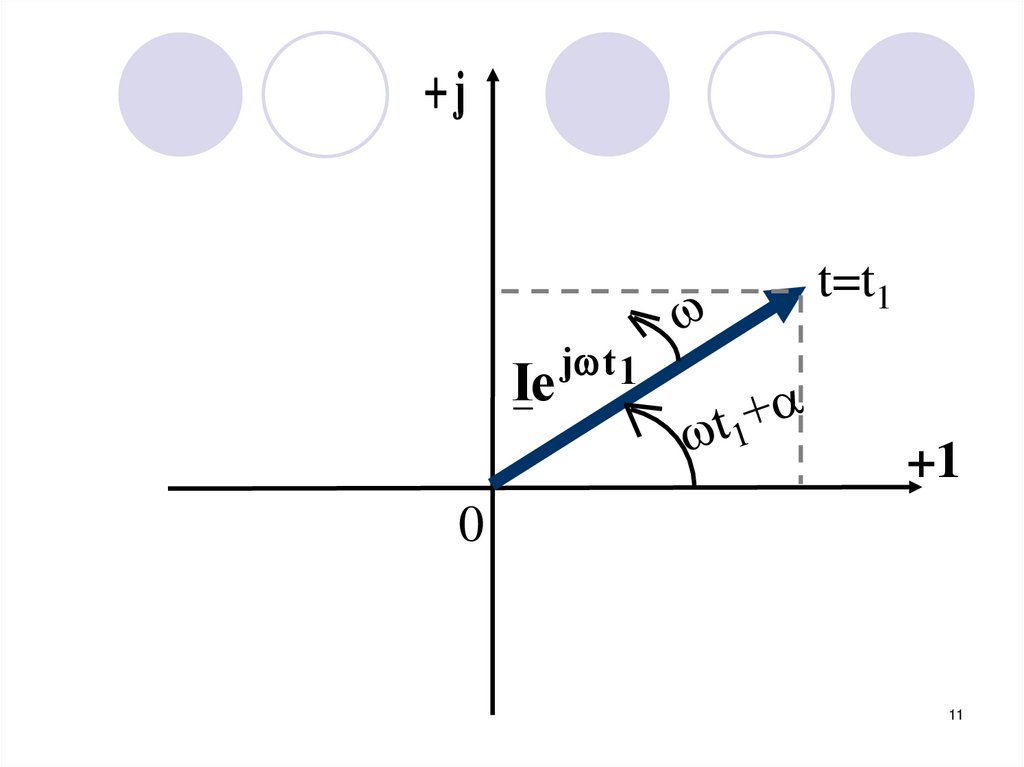
11.
jt=t1
Ie
j t 1
+1
0
11
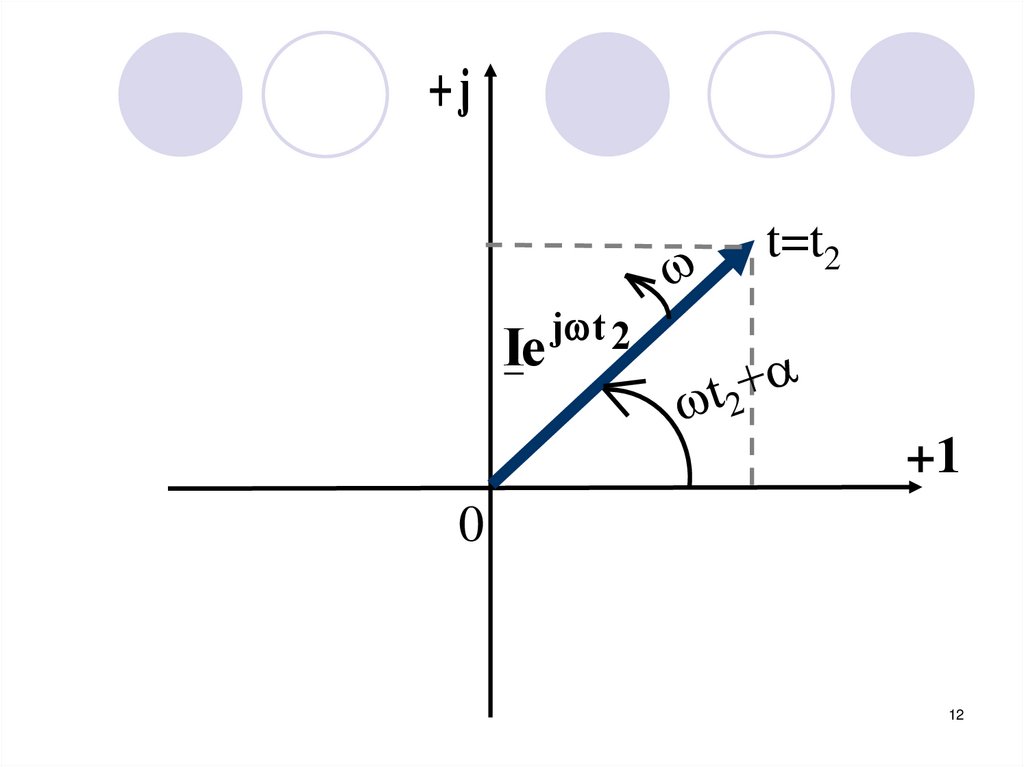
12.
jt=t2
Ie
j t 2
+1
0
12
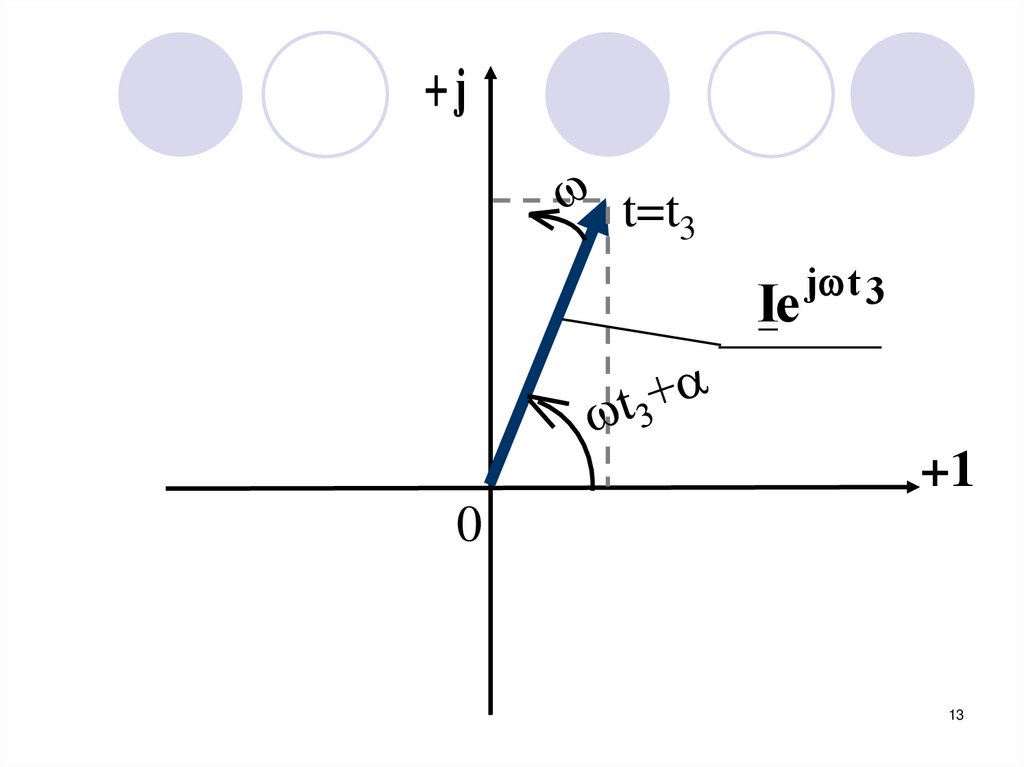
13.
jt=t3
Ie
j t 3
+1
0
13
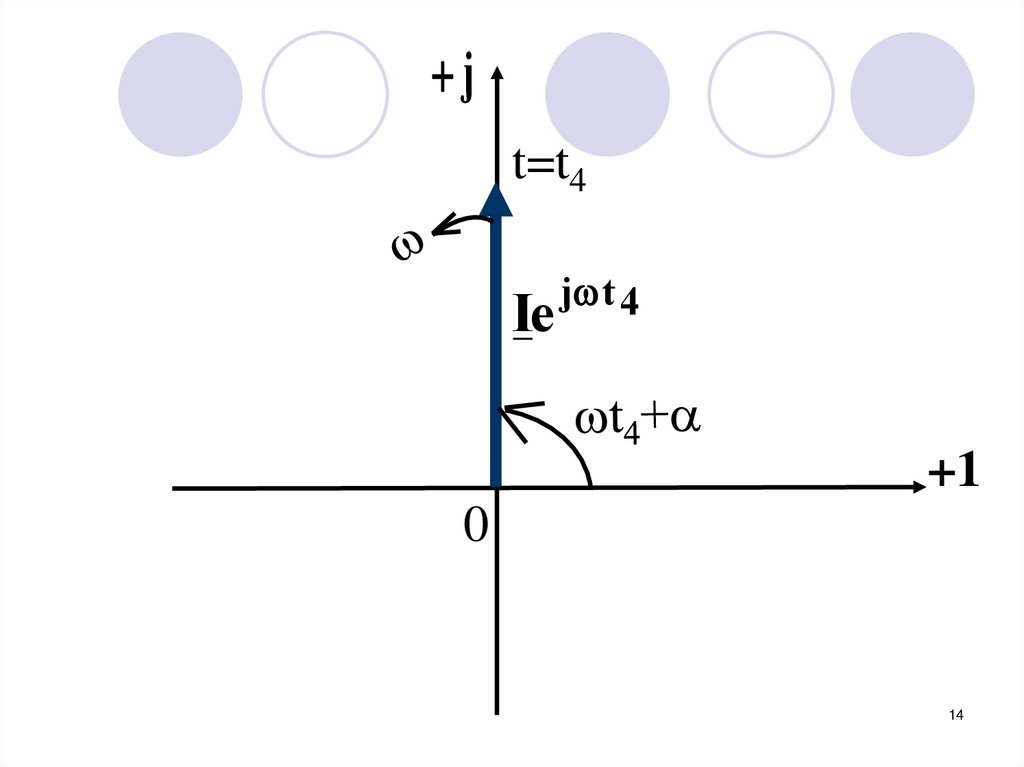
14.
jt=t4
Ie
j t 4
+1
0
14
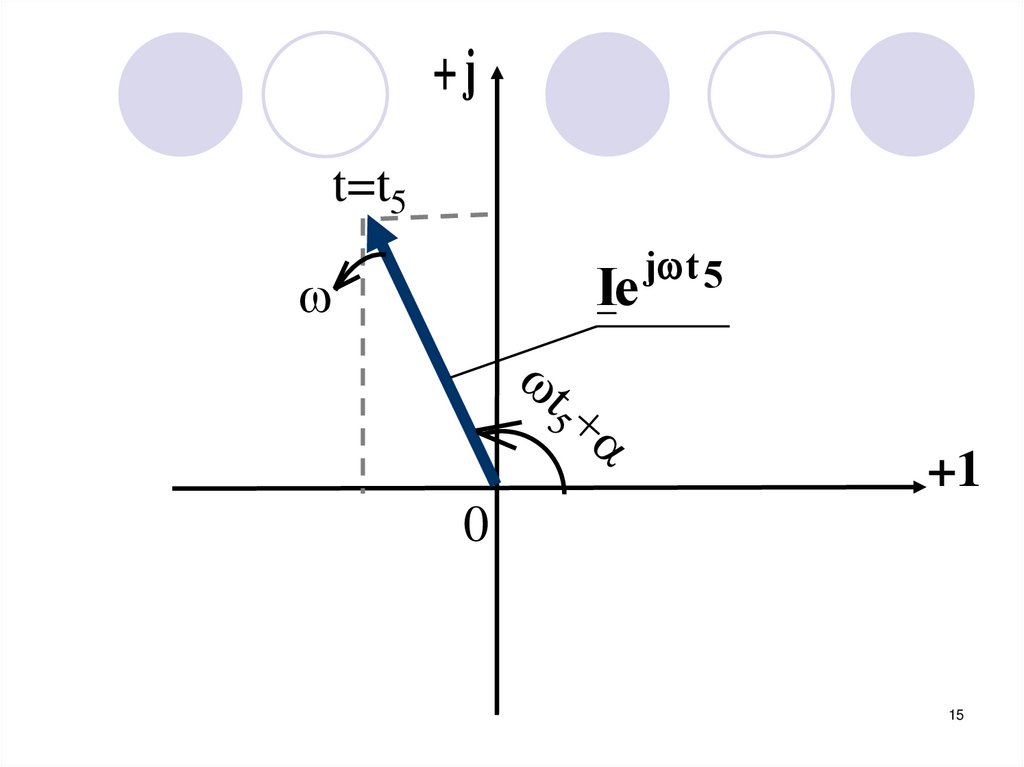
15.
jt=t5
Ie
j t 5
+1
0
15
16.
Таким образом любойсинусоидальной величине
(току или напряжению)
соответствует комплекс ее
действующего значения и
наоборот
Например: току
i 2.82 sin( t 30 ), А
соответствует
2.82 j30
I I
e
2
16
17.
При этом, например, комплексудействующего значения
напряжения
U U 100 e
j45
,В
соответствует синусоидальная
функция времени
u 2 100 Sin ( t 45 ), В
17
18.
Действияс комплексными
числами
18
19.
Где:F F e
j
a jb - комплексное
число
F - модуль
- аргумент (фаза)
a - вещественная составляющая
b - мнимая составляющая
19
20.
1. Переход от алгебраическойформы записи
к показательной форме
20
21.
a jb Fe2
F a b
j
2
b
(180) arctg
a
21
22.
При этом 180 градусовучитывается при а<0
22
23.
2. Переход от показательнойформы записи
к алгебраической форме
23
24.
Fej
a jb
a F cos
b F sin
24
25.
3. Сложение и вычитание25
26.
F1ej 1
F2e
j 2
(a1 jb 1 ) (a 2 jb 2 )
(a1 a 2 ) j(b1 b 2 )
j
a jb Fe .
26
27.
4. Умножение27
28.
(a1 jb1 )(a 2 jb 2 )F1e
j 1
F1F2e
j 2
j( 1 2 )
F2e
j
Fe .
28
29.
5. Деление29
30.
j 1a1 jb1 F1e
j 2
a 2 jb 2 F2e
F1 j( 1 2 )
e
F2
j
Fe .
30
31.
6. Возведение в степень31
32.
m(a1 jb1 )
(F1e
j 1 m
)
m jm 1
F1 e
j
Fe .
32
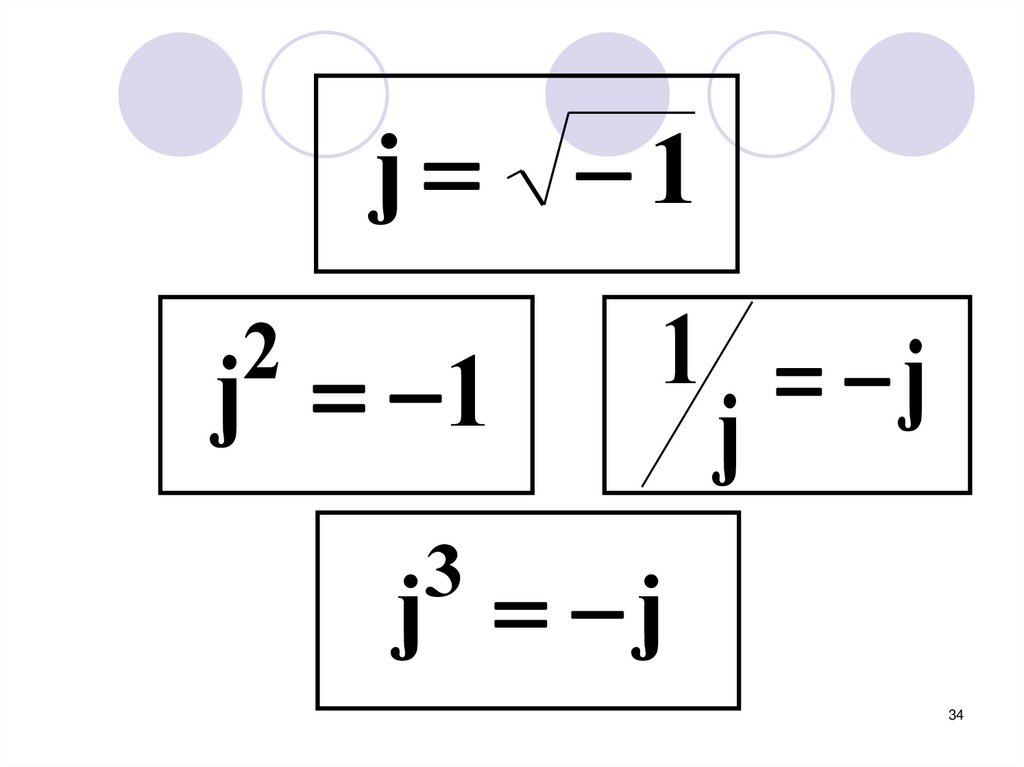
33.
7. Некоторые соотношения33
34.
j 12
j 1
1 j
j
3
j j
34
35.
j ej90
1 e
j0
j e
j90
1 e
j180
35
36.
Действияс синусоидальными
величинами
36
37.
Рассмотрим действияс синусоидальными
величинами, имеющими
одинаковую угловую
частоту
37
38.
1. Сложение38
39.
f (t ) 2F sin( t )f1 ( t ) f 2 ( t )
39
40.
f1 (t ) 2F1 sin( t 1 )F1 F1e
j 1
f 2 (t ) 2F2 sin( t 2 )
F 2 F2e
j 2
40
41.
Для определенияF и
используются:
41
42.
а) комплексные числаj 2
Fе
определяются
F и
F1е
j 1
F2е
j
42
43.
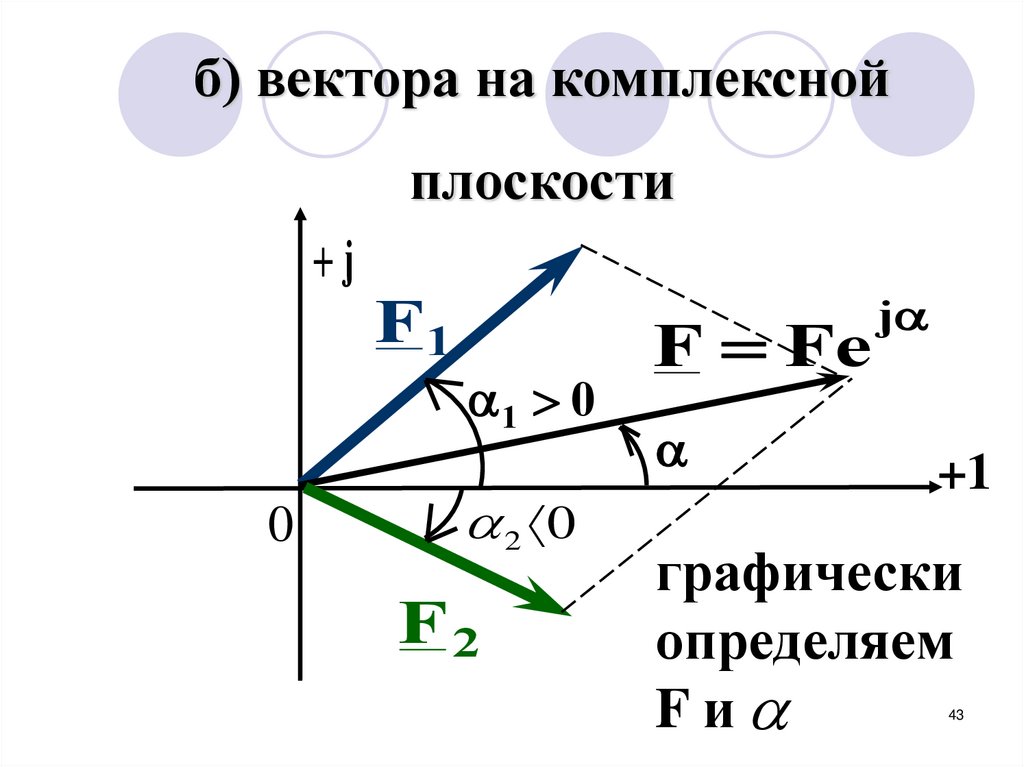
б) вектора на комплекснойплоскости
j
F1
1 0
0
2 0
F2
F Fe
j
+1
графически
определяем
Fи
43
44.
2. Вычитание44
45.
f (t ) 2F sin( t )f1 ( t ) f 2 ( t )
45
46.
f1 ( t )f 2 (t )
F1 F1e
j 1
F 2 F2e
j 2
46
47.
Для определенияF и
используются:
47
48.
а) комплексные числаj 2
Fе
определяются
F и
F1е
j 1
F2е
j
48
49.
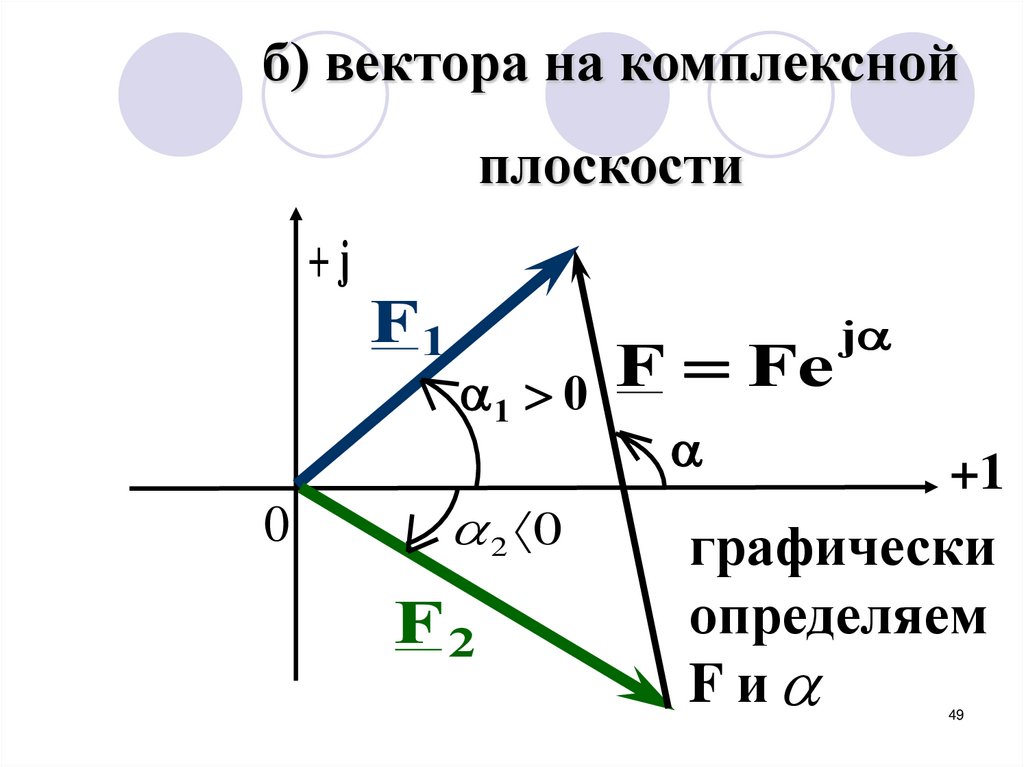
б) вектора на комплекснойплоскости
j
F1
F
Fe
0
1
0
2 0
F2
j
+1
графически
определяем
Fи
49
50.
3. Дифференцирование50
51.
f (t ) 2F sin( t )F Fe
j
df (t )
2 F sin( t 90 )
dt
Fe
j( 90 )
j F
51
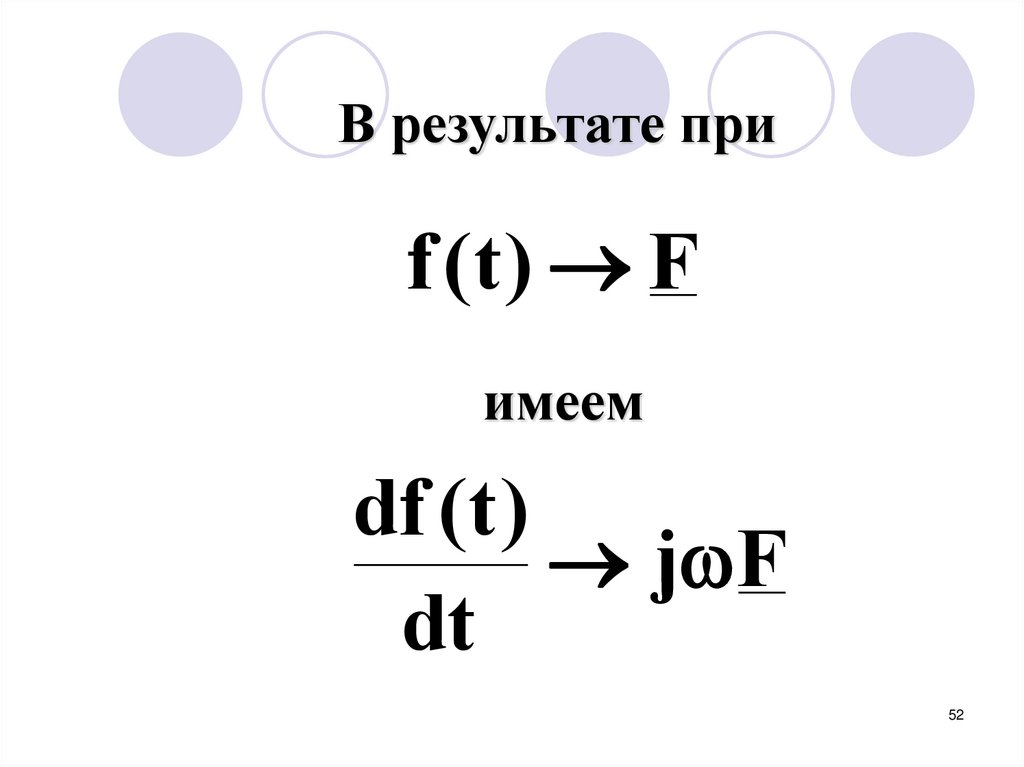
52.
В результате приf (t ) F
имеем
df (t )
j F
dt
52
53.
Таким образомдифференцированию
синусоидальной функции
соответствует умножение
изображающего ее комплекса
на j
53
54.
4. Интегрирование54
55.
f (t ) 2F sin( t )F Fe
j
2F
f (t )dt
sin( t 90 )
F j( 90 ) F
e
j
55
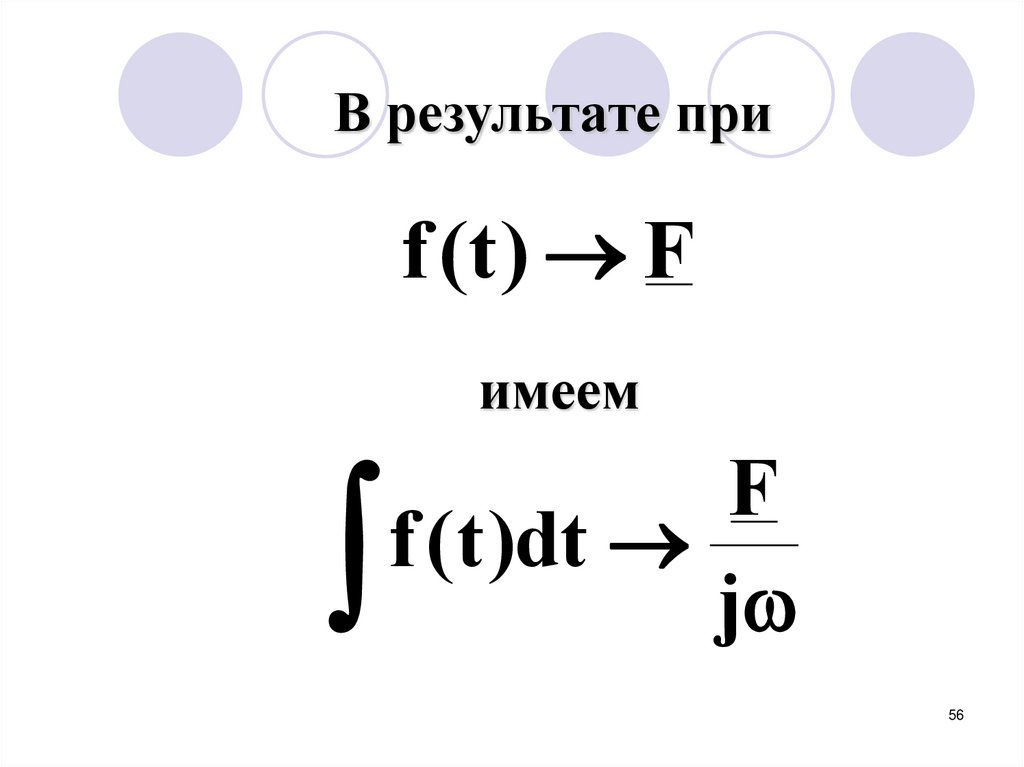
56.
В результате приf (t ) F
имеем
F
f (t )dt
j
56
57.
Таким образом интегрированиюсинусоидальной функции
соответствует деление
изображающего ее комплекса
на j
57
58.
ЗАКОН ОМАВ КОМПЛЕКСНОЙ
ФОРМЕ
58
59.
Закон Ома в комплексной формеоснован на символическом методе
и справедлив для линейных цепей
с гармоническими напряжениями
и токами
Этот закон следует из
физической взаимосвязи
между током и напряжением
отдельных элементов цепи
59
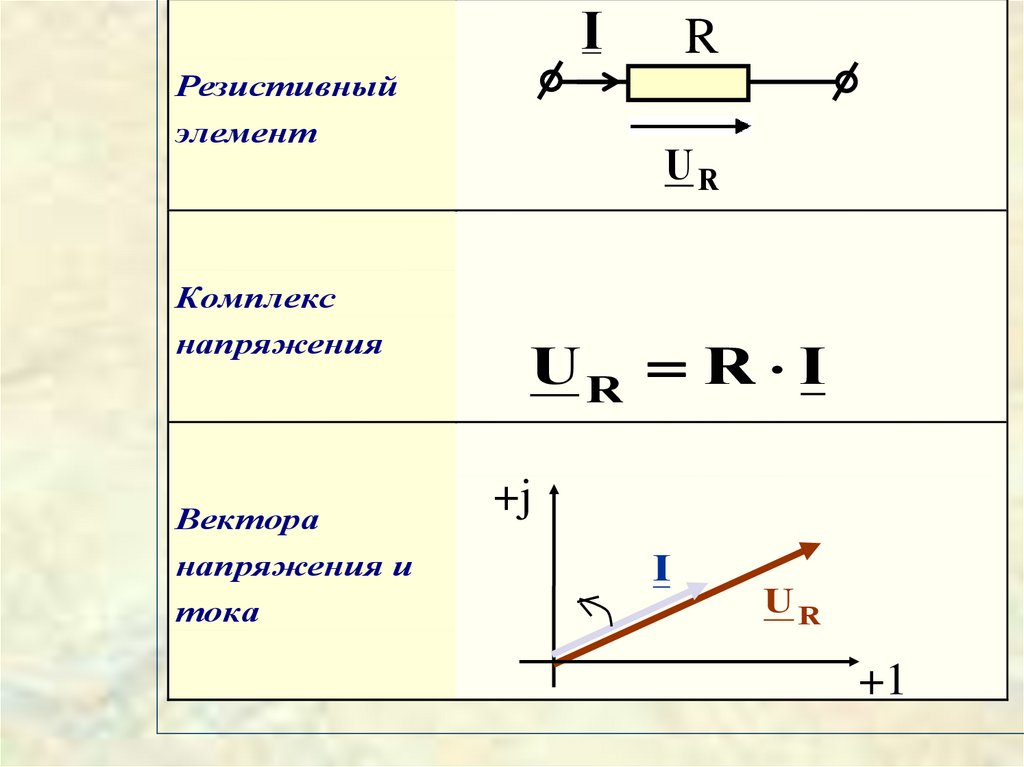
60.
IR
Резистивный
элемент
UR
Комплекс
напряжения
Вектора
напряжения и
тока
UR R I
+j
I
UR
+1
60
61.
На комплексной плоскостивектор напряжения
резистивного элемента
совпадает по направлению
с вектором своего тока
61
62.
Индуктивныйэлемент
Комплекс
напряжения
U L j LI jX L I
+j
Вектора
напряжения и
тока
UL
I
+1
62
63.
На комплексной плоскостивектор напряжения
индуктивного элемента
опережает по направлению
вектор своего тока
на 90 градусов
63
64.
ЕмкостныйI
элемент
Комплекс
напряжения
jXC
UC
j
UC
I jX C I
C
+j
I
Вектора
напряжения и
тока
+1
UC
64
65.
На комплексной плоскостивектор напряжения
емкостного элемента
отстает по направлению
от вектора своего тока
на 90 градусов
65
66.
Где:X L L
XC 1
- индуктивное
сопротивление (Ом)
- емкостное
C
сопротивление (Ом)
66
67.
Закон Ома в комплексной формедля отдельных элементов аналогичен
закону Ома для резистивного элемента
на постоянном токе
Для символического метода
необходимо составить комплексную
схему замещения с комплексными
сопротивлениями и с комплексами
действующих значений токов и
напряжений
67
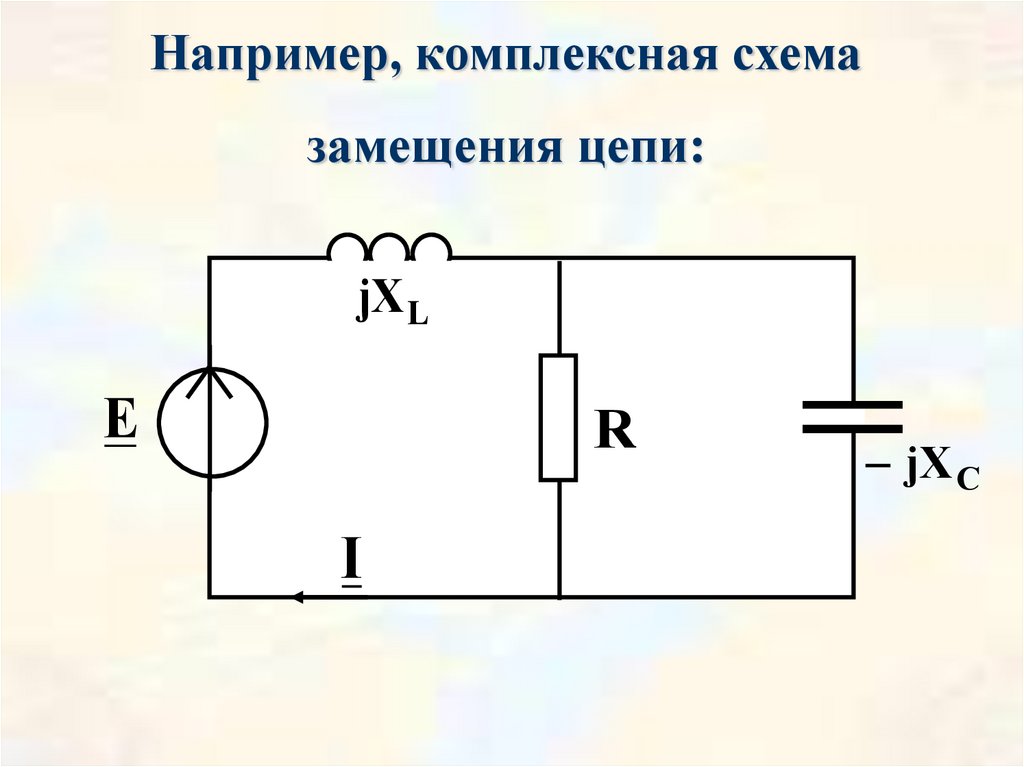
68.
Например, комплексная схемазамещения цепи:
jX L
E
R
jX C
I
68
69.
R( jX C )Z jX L
R jX C
E
I
Z
69
70.
Где:j
Z RЭ jX Э Z e
– эквивалентное комплексное
сопротивление цепи (Ом)
2
2
Z RЭ X Э
- модуль сопротивления (Ом)
XЭ
arctg
RЭ
-аргумент (фаза)
сопротивления (Град)
70

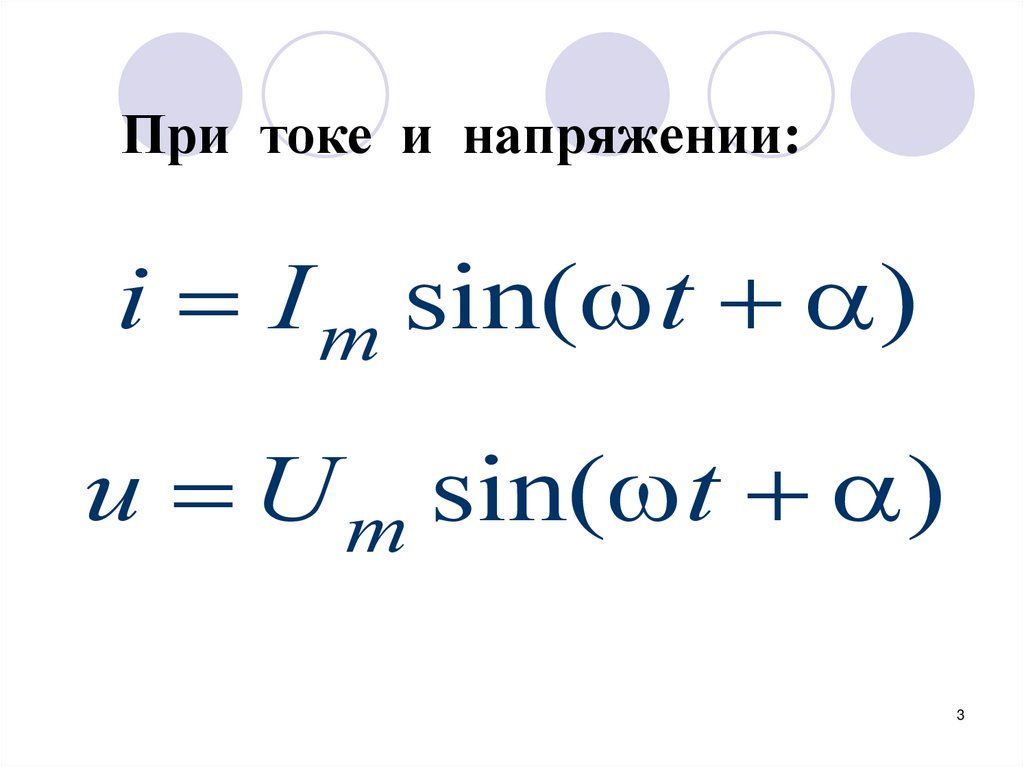










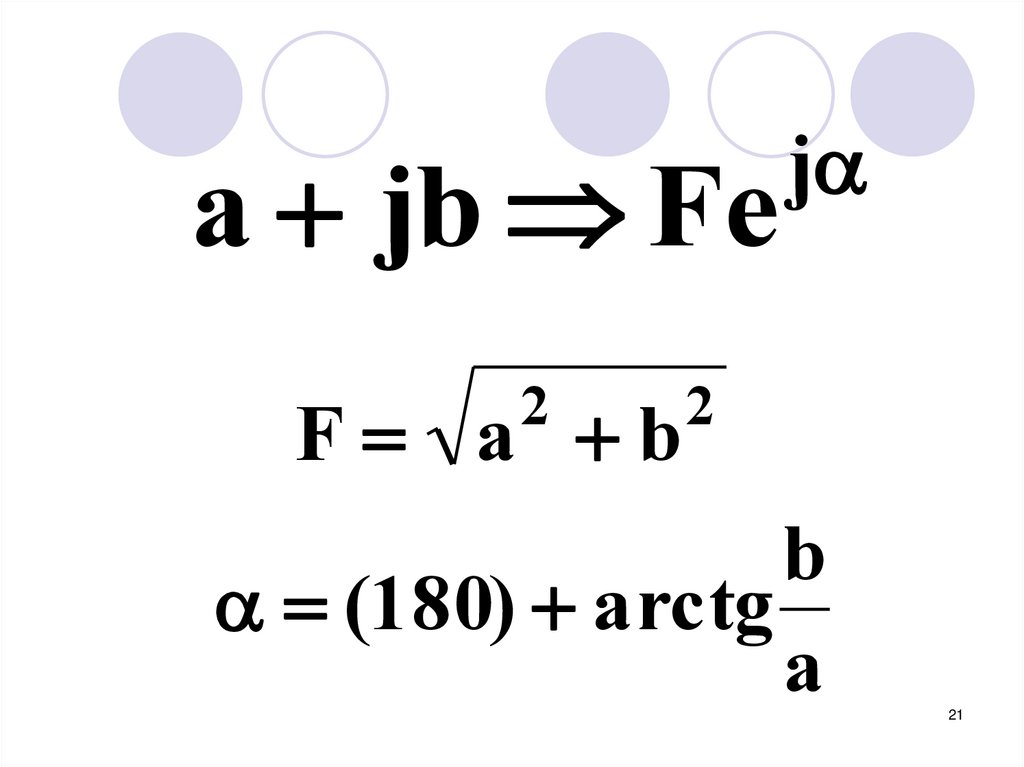




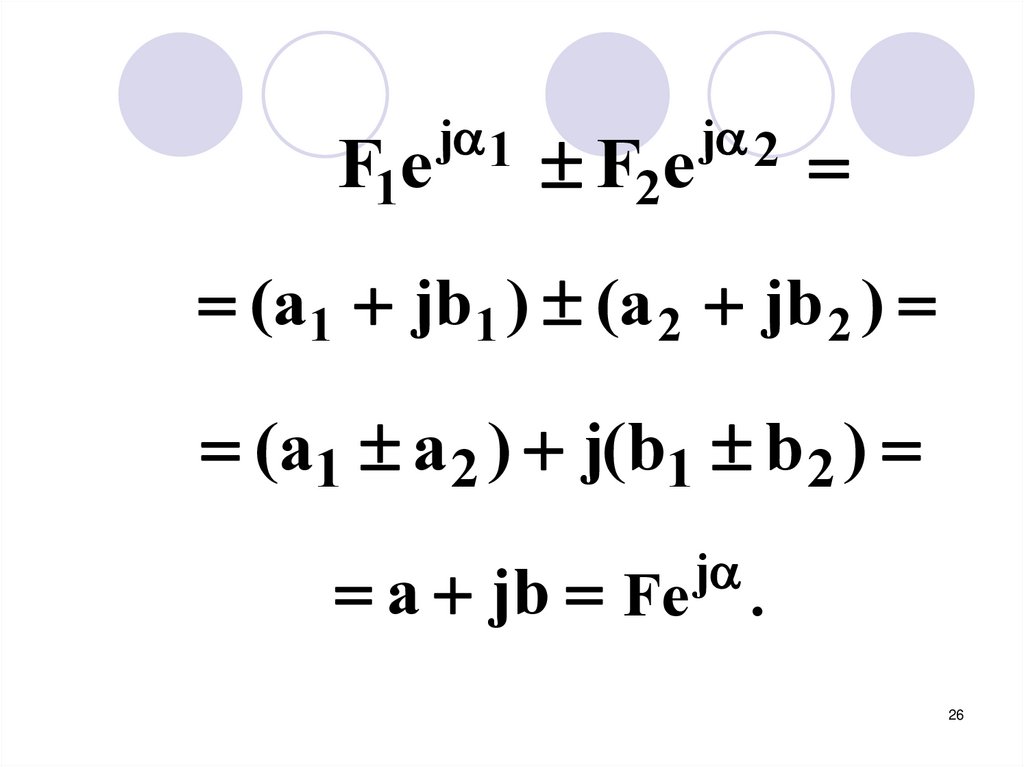

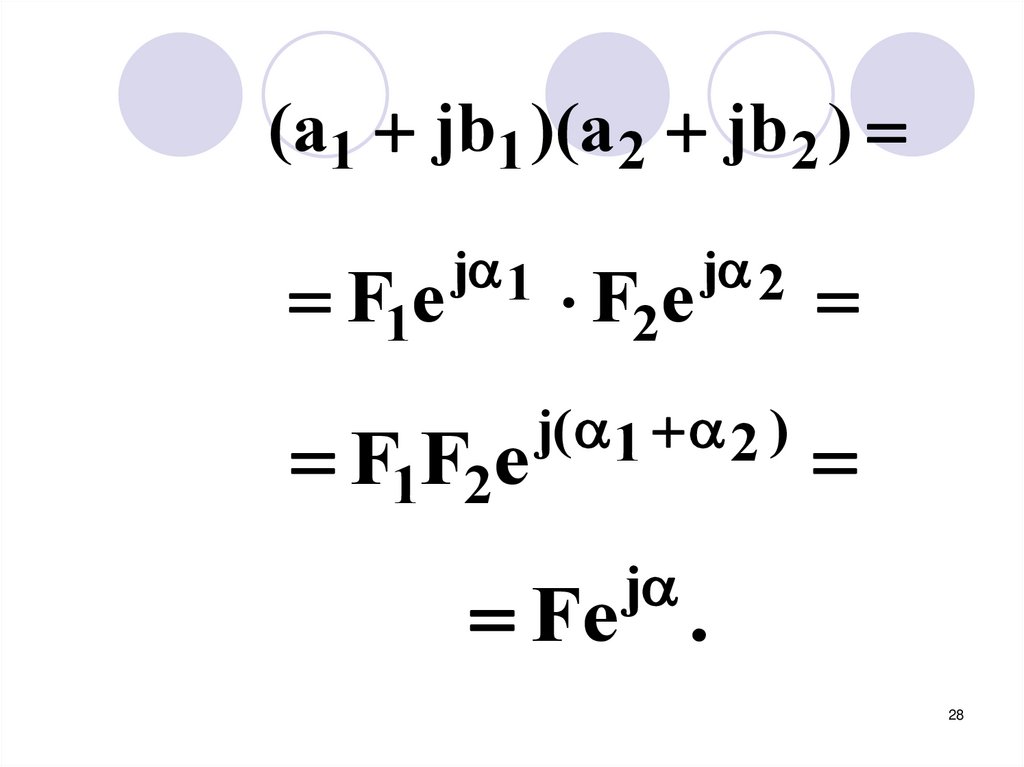

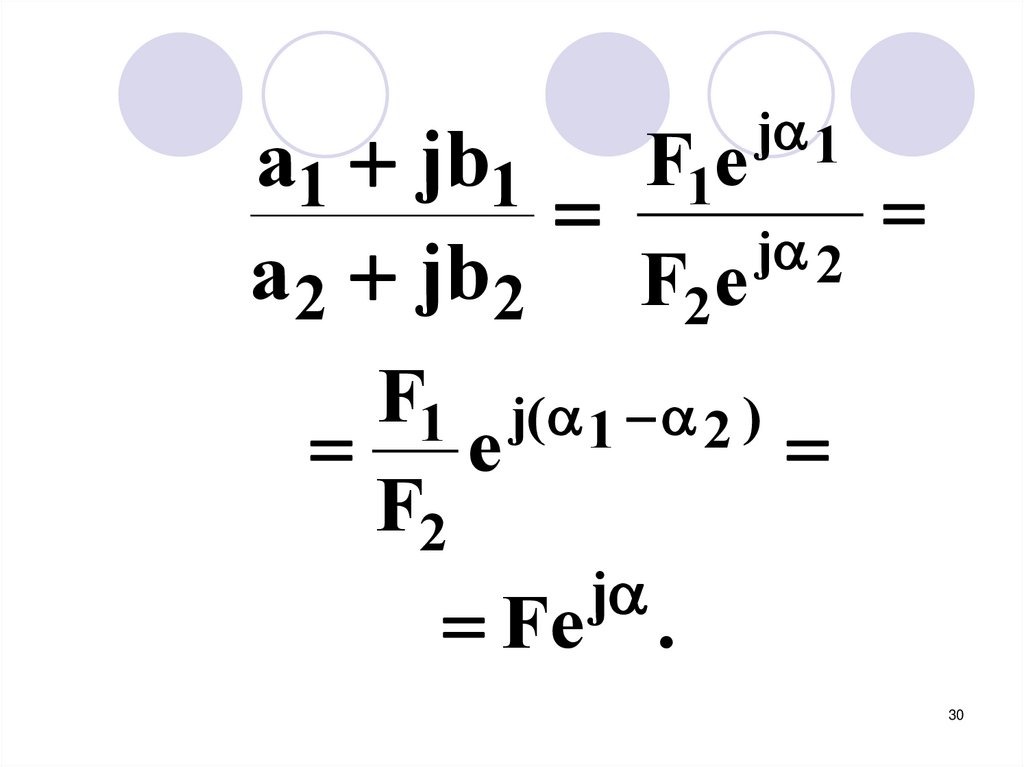

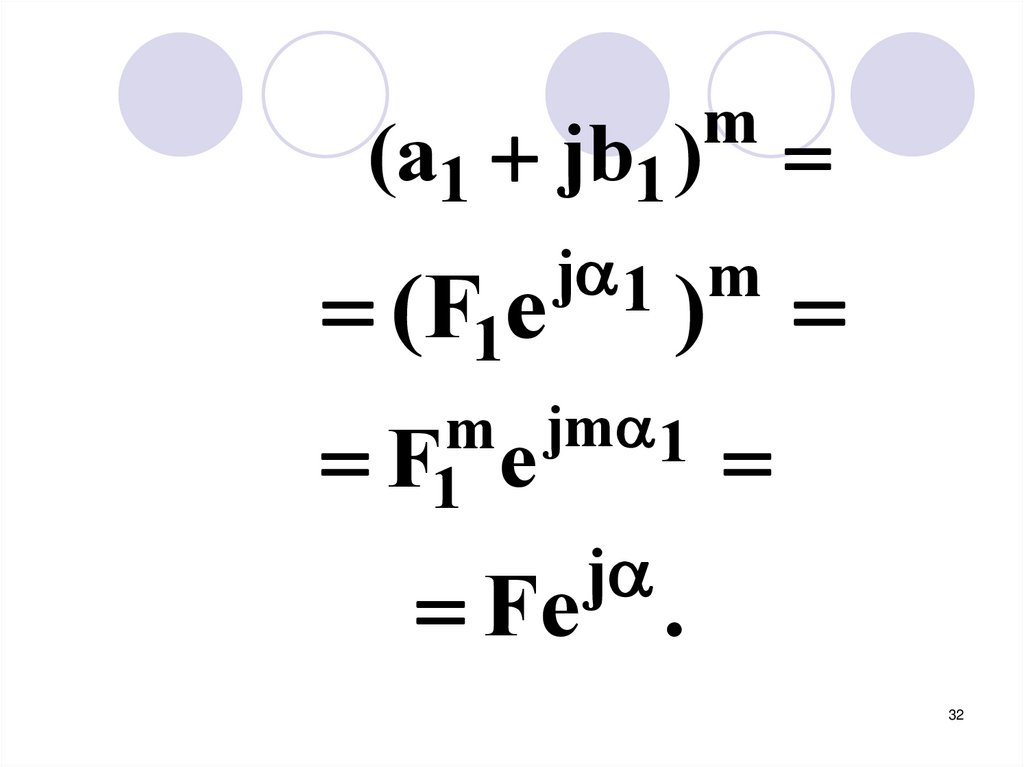

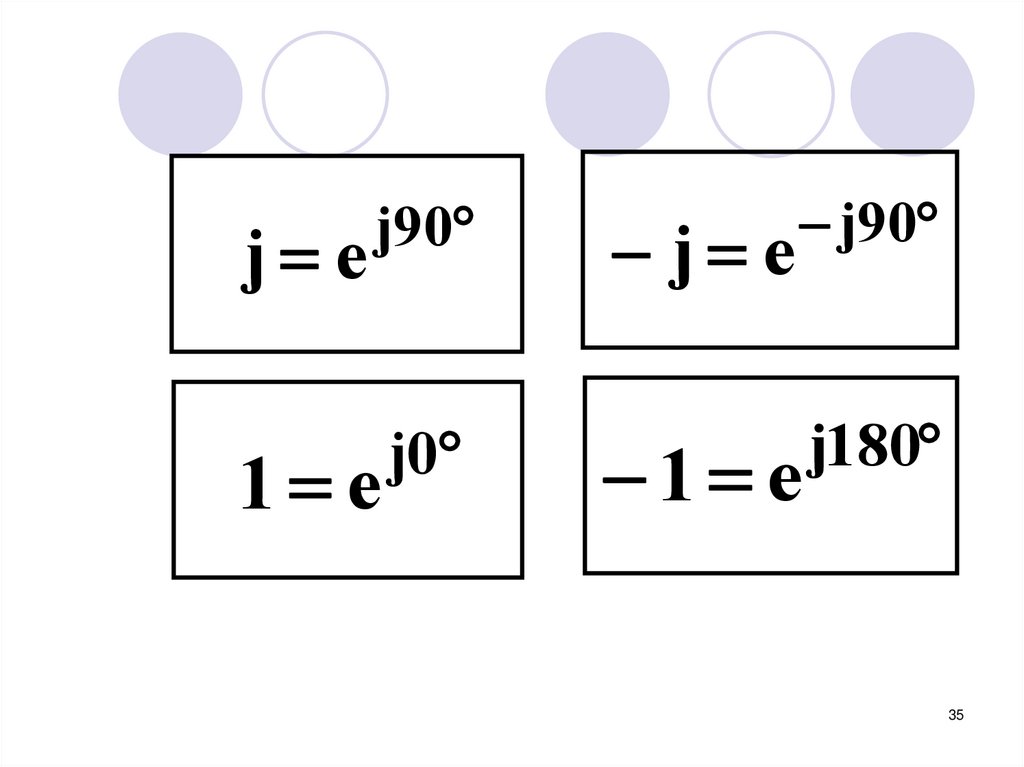



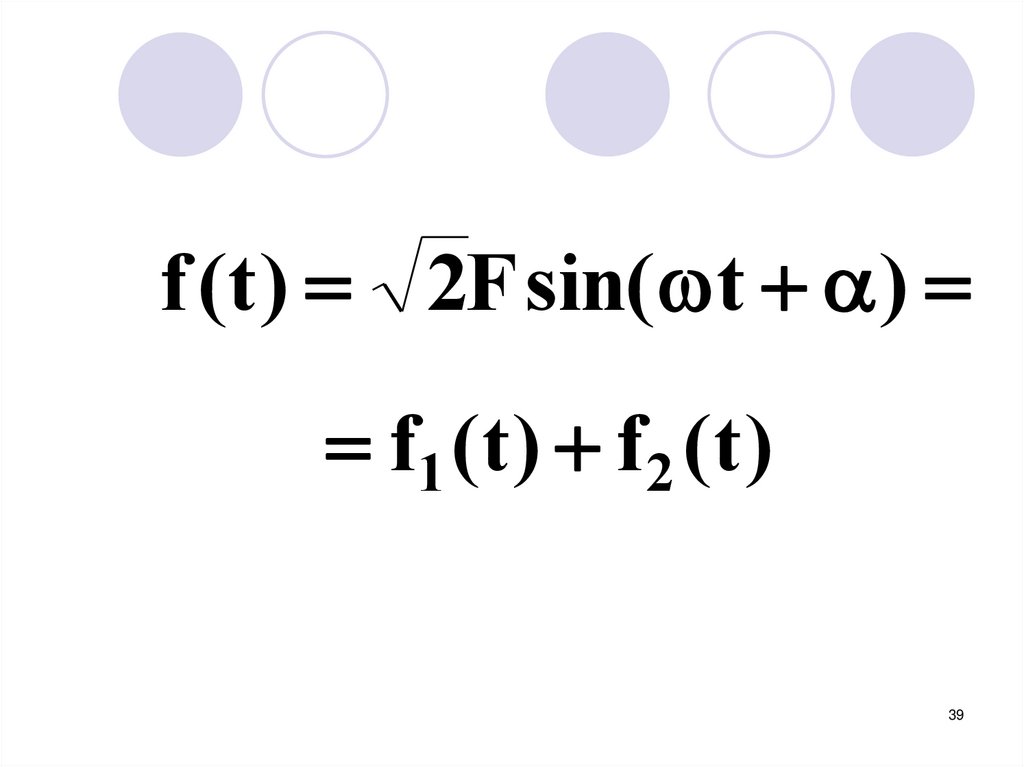
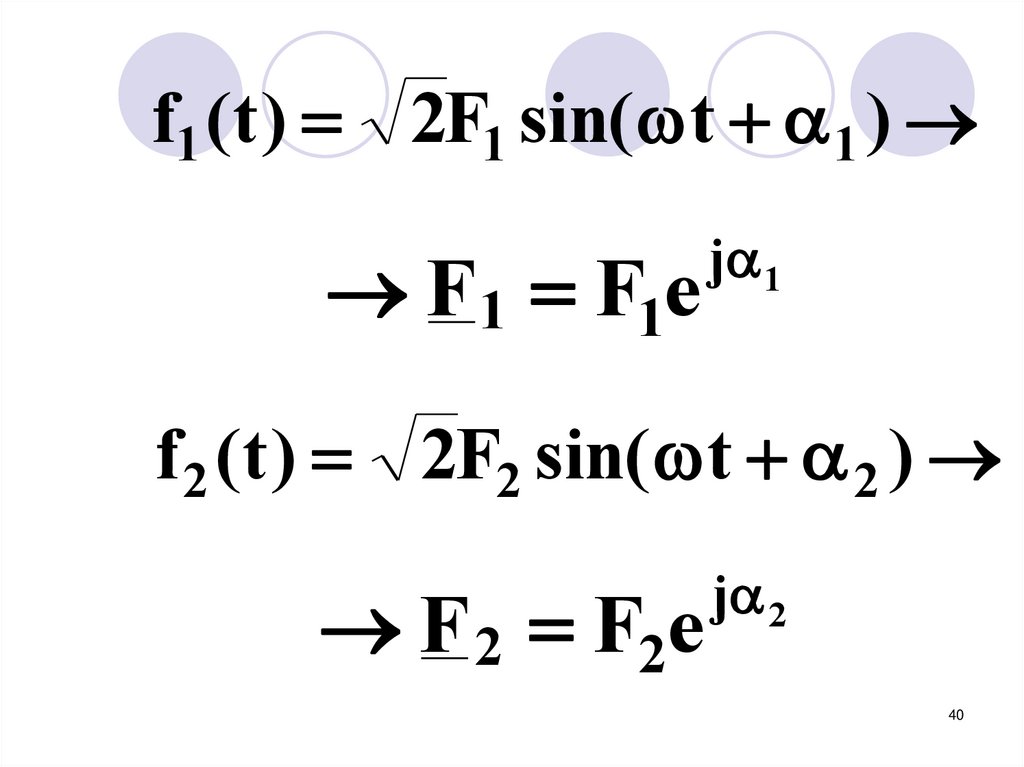

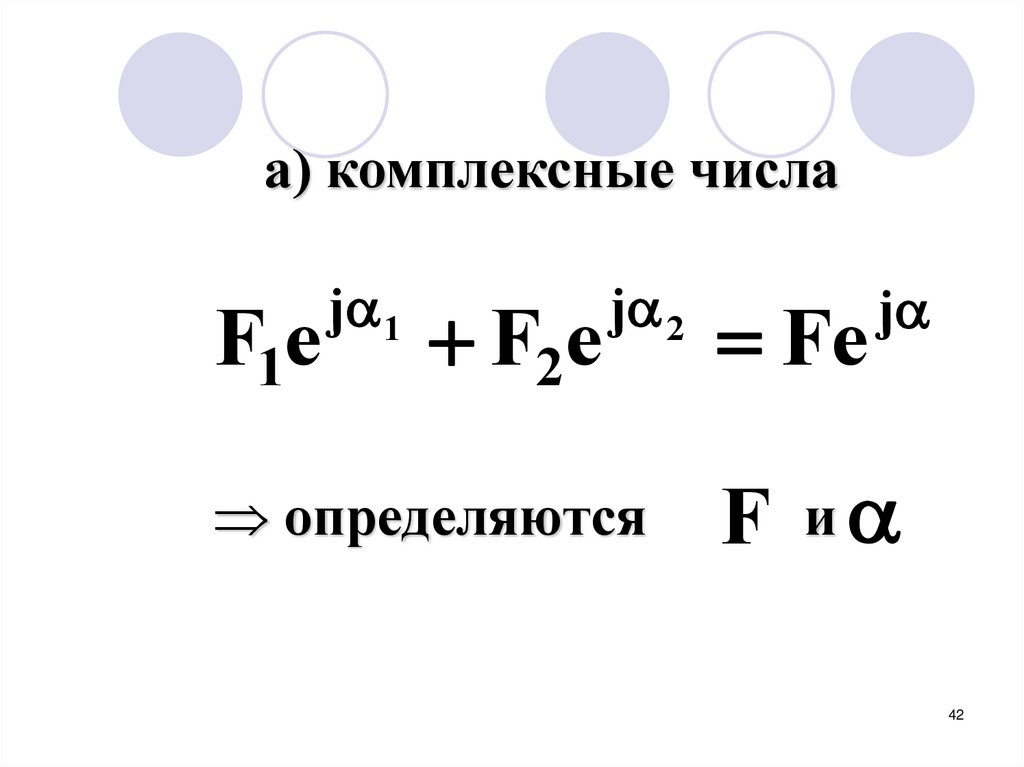

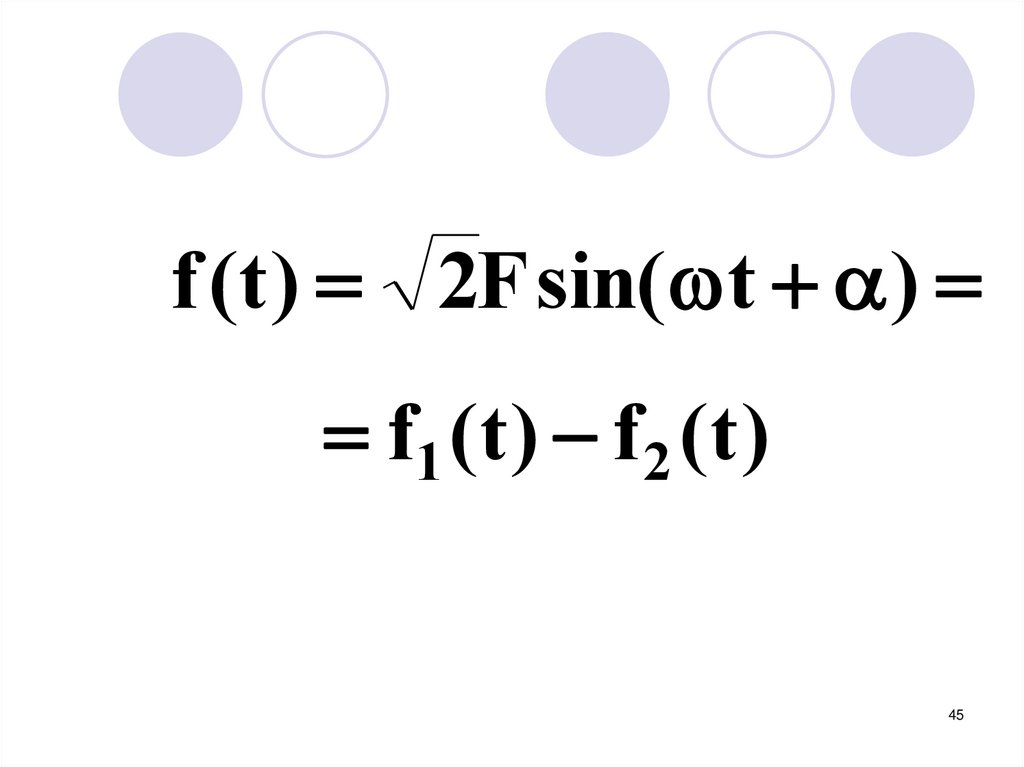
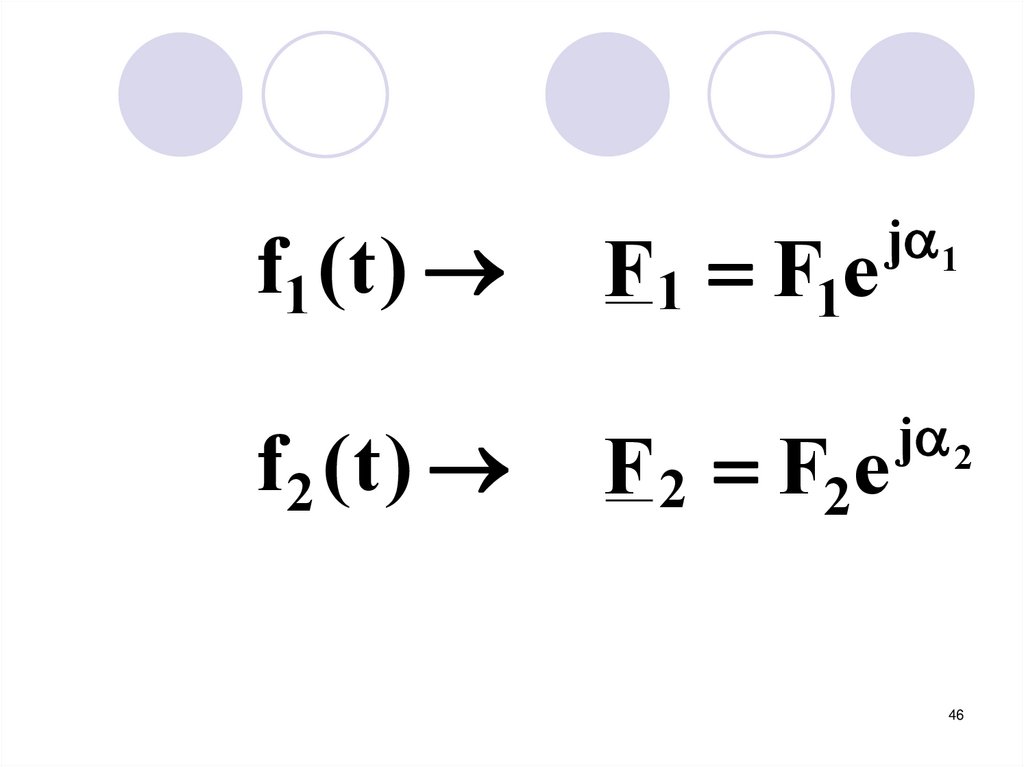

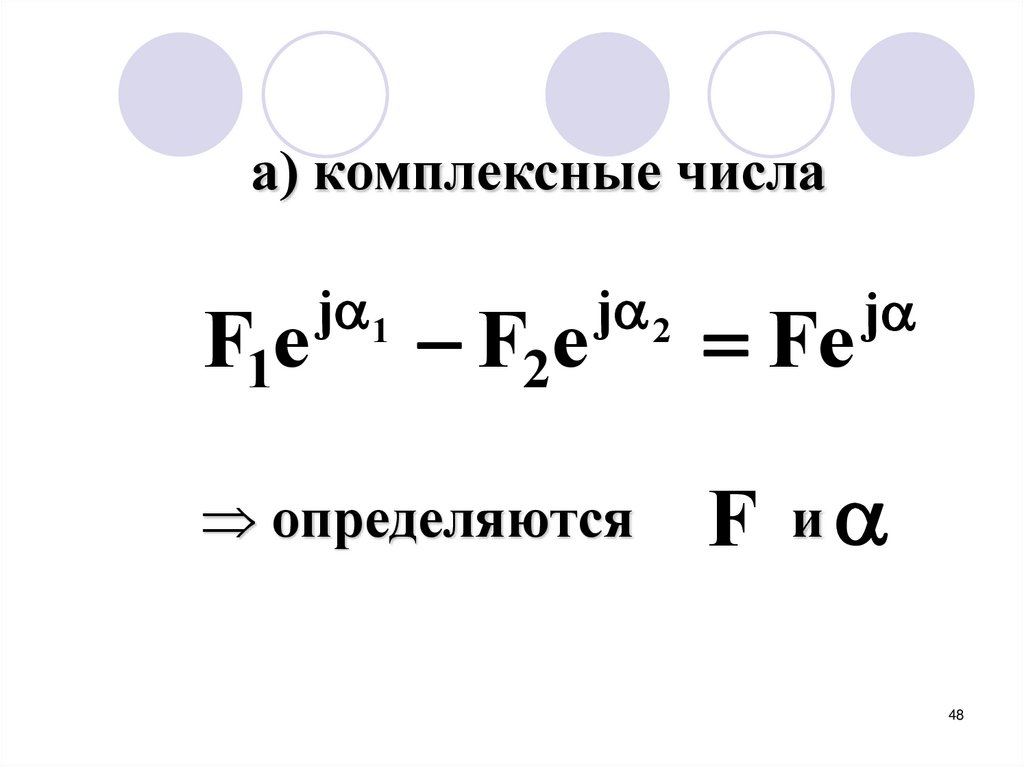

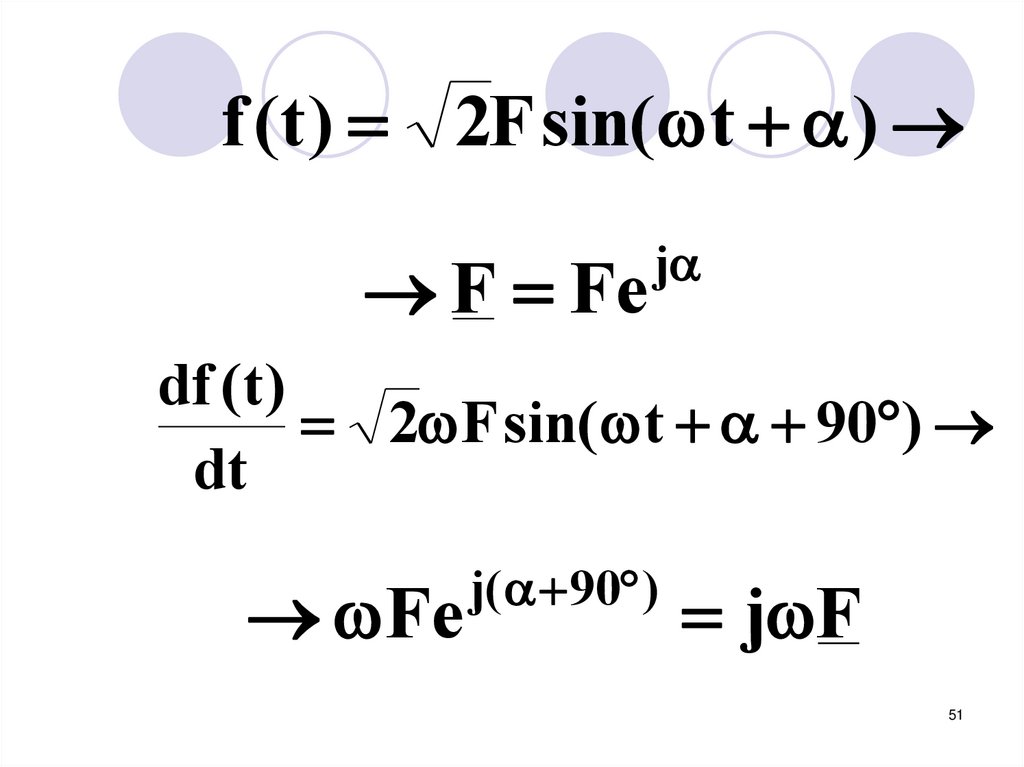


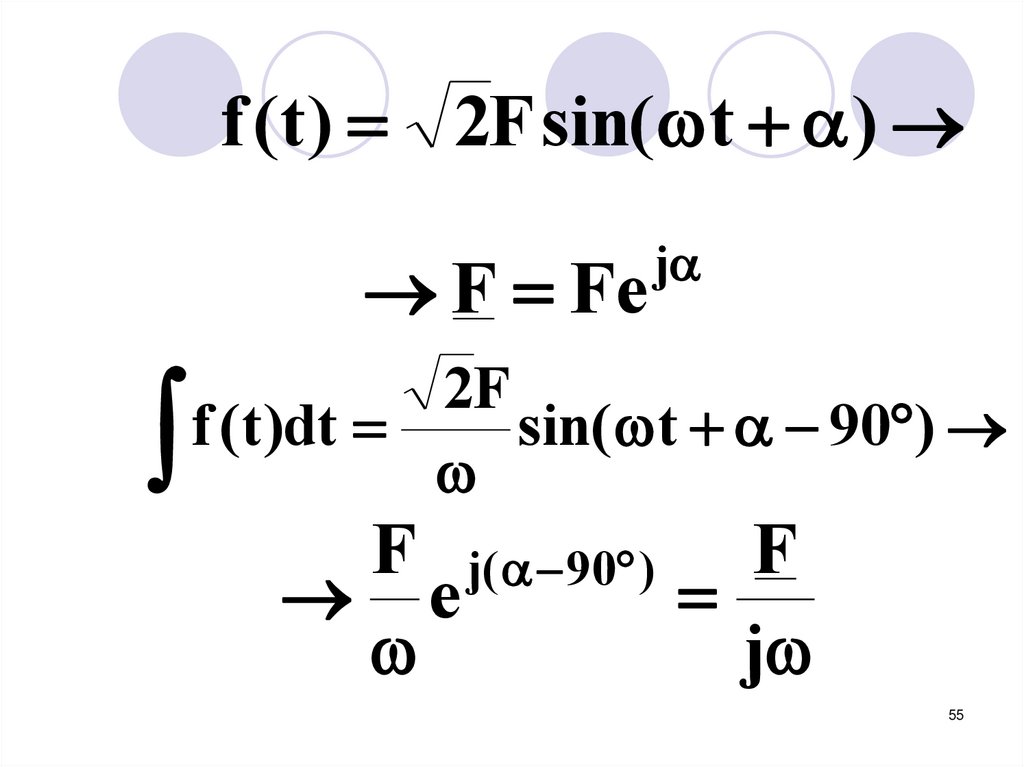










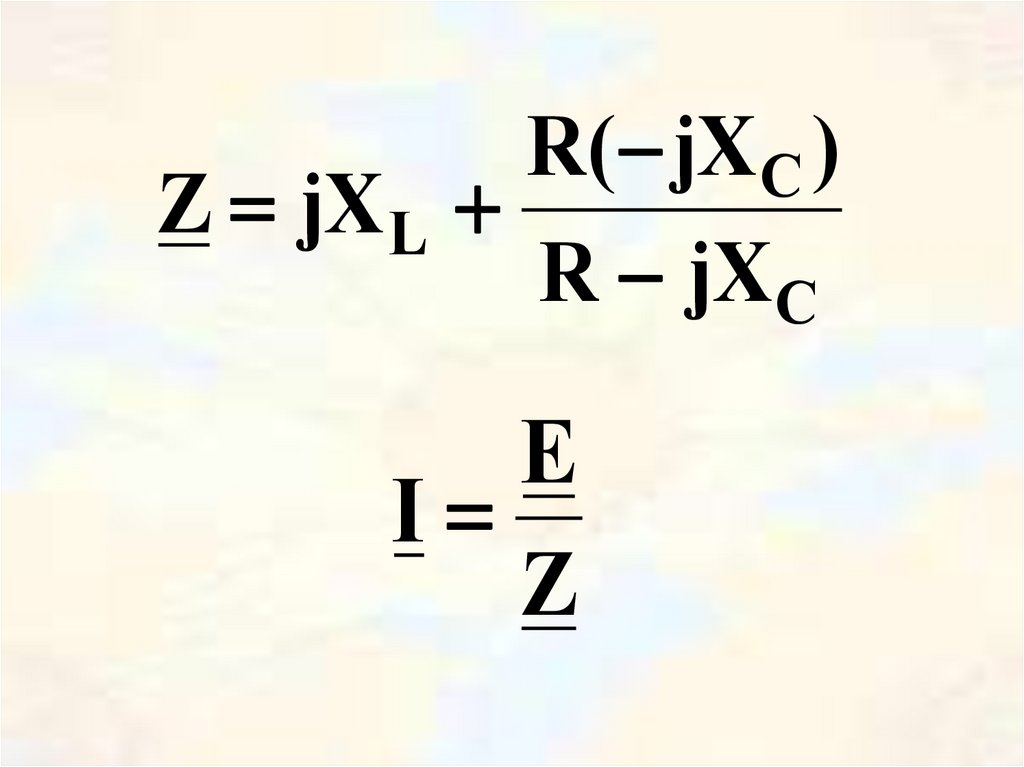

 physics
physics








