Линейные электрические цепи переменного однофазного тока. Получение синусоидальной ЭДС

1. Линейные электрические цепи переменного однофазного тока Получение синусоидальной эдс

Лекция 3
Линейные электрические цепи
переменного однофазного тока
Получение синусоидальной эдс
Целесообразность применения энергии переменного тока
Основные параметры цепей синусоидального тока
Способы представления синусоидальных величин
Элементы R, L, C в электрической цепи синусоидального тока
Мощности в цепях синусоидального тока
i(t) = Im sin(ωt + ψi)

2. Получение синусоидальной эдс

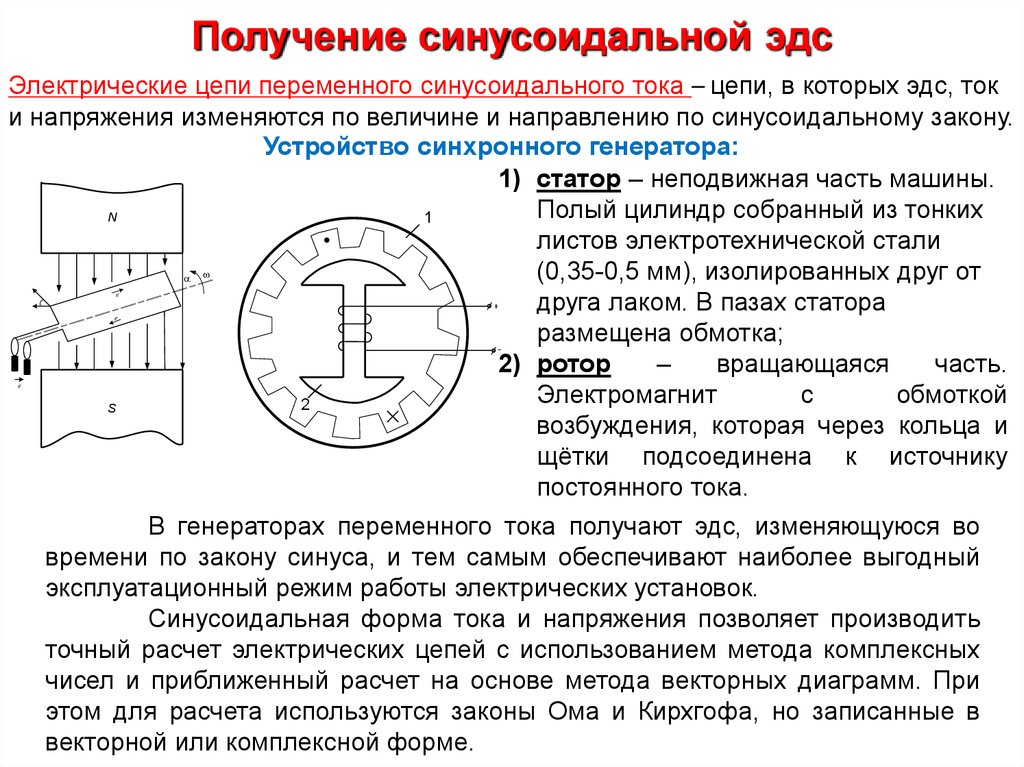
Электрические цепи переменного синусоидального тока – цепи, в которых эдс, ток
и напряжения изменяются по величине и направлению по синусоидальному закону.
Устройство синхронного генератора:
1) статор – неподвижная часть машины.
Полый цилиндр собранный из тонких
N
1
листов электротехнической стали
(0,35-0,5 мм), изолированных друг от
друга лаком. В пазах статора
размещена обмотка;
2) ротор
–
вращающаяся
часть.
Электромагнит
с
обмоткой
2
S
возбуждения, которая через кольца и
щётки подсоединена к источнику
постоянного тока.
e
e
e
В генераторах переменного тока получают эдс, изменяющуюся во
времени по закону синуса, и тем самым обеспечивают наиболее выгодный
эксплуатационный режим работы электрических установок.
Синусоидальная форма тока и напряжения позволяет производить
точный расчет электрических цепей с использованием метода комплексных
чисел и приближенный расчет на основе метода векторных диаграмм. При
этом для расчета используются законы Ома и Кирхгофа, но записанные в
векторной или комплексной форме.

3. Целесообразность применения энергии переменного тока

В настоящее время почти вся электрическая энергия вырабатывается
в виде энергии переменного тока. Это объясняется преимуществом
производства и распределения этой энергии.
Переменный ток получают
на электростанциях, преобразуя с помощью генераторов механическую
энергию в электрическую.
Основные преимущества переменного тока по сравнению с постоянным:
- генераторы синусоидального тока значительно дешевле в производстве,
чем генераторы постоянного тока;
- переменный ток легко преобразуется в постоянный;
- трансформация и передача электрической энергии переменным током
экономичнее чем постоянным;
- двигатели переменного тока имеют простую конструкцию, высокую
надежность и невысокую стоимость.

4. Основные параметры цепей синусоидального тока

, представлен посредством
Синусоидальный ток может быть
действительной функции времени:
i
i Im sin( t i )
Im
Значение тока, напряжения, эдс в любой момент
t
времени t называется мгновенным значением и
обозначается малыми строчными буквами,
соответственно i, u, e.
Im - максимальная амплитуда тока (амплитудное значение);
- угловая частота [1/c] или [рад/c];
=2pf;
f - частота колебаний [Гц];
Т - период [с];
T=2p;
i - начальная фаза,
t i - фаза, рад;
c
i
T
2p
Действующее значение тока обозначается I:
R
T
I
T
I rT i rdt
2
0
2
T
1 2
I
i dt
T 0
T
T 1 cos2( t )dt I
1
1
2
2
i
I
I r sin ( t i )dt Im
m 0,707 Im
T0
T0
2
2
i
Измерительные приборы показывают действующие значения.
R
T

5.

Способы представления синусоидальных токов,
напряжений, эдс
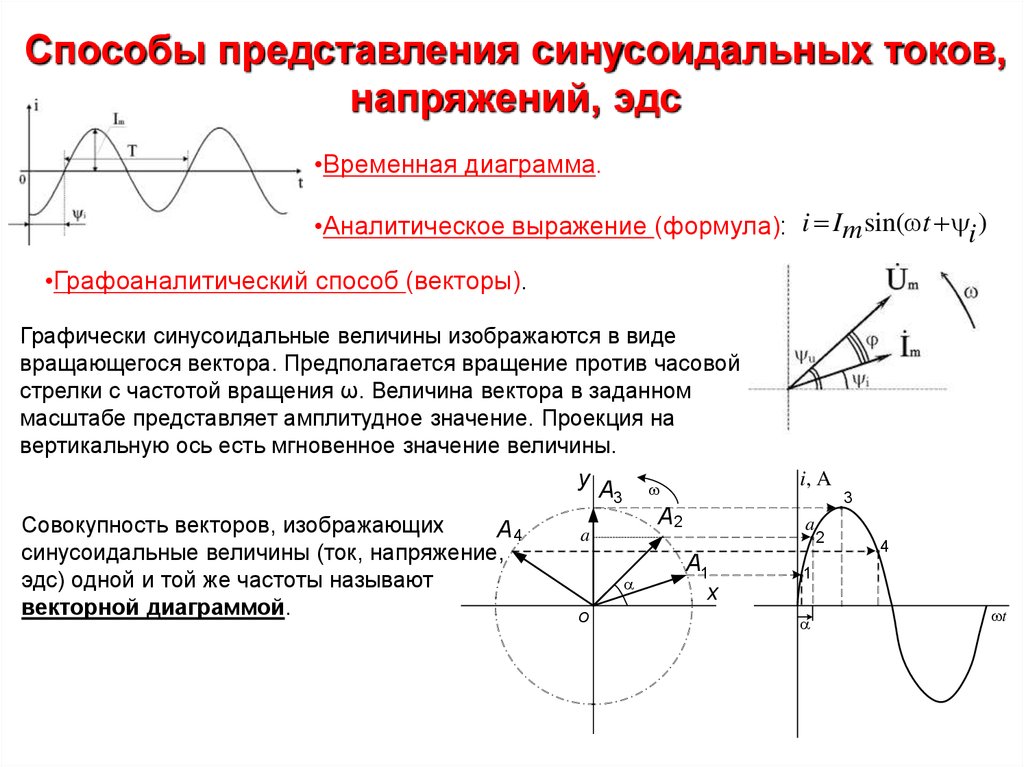
•Временная диаграмма.
•Аналитическое выражение (формула): i Im sin( t i )
•Графоаналитический способ (векторы).
Графически синусоидальные величины изображаются в виде
вращающегося вектора. Предполагается вращение против часовой
стрелки с частотой вращения ω. Величина вектора в заданном
масштабе представляет амплитудное значение. Проекция на
вертикальную ось есть мгновенное значение величины.
yA
3
Совокупность векторов, изображающих
A4
синусоидальные величины (ток, напряжение,
эдс) одной и той же частоты называют
векторной диаграммой.
3
A2
a
o
i, A
a
A1
x
2
4
1
t

6.

Способы представления синусоидальных токов,
напряжений, эдс
+j
Синусоидальный ток можно представить комплексным
j
числом Ím на комплексной плоскости:
I I e i
m
m
где амплитуда тока Im – модуль, а угол ψ, являющийся
начальной фазой, т.е. аргумент комплексного тока.
b
Im
t+
•Комплексные числа.
0
+1
a
Комплексное действующее значение тока Í :
j i
Im
I Ie
2
Символический метод расчёта цепей синусоидального тока - использование
комплексной формы представления позволяет заменить геометрические
операции над векторами алгебраическими операциями над комплексными
числами. В результате этого к анализу цепей переменного тока могут быть
применены все методы анализа цепей постоянного тока.

7. Основные формы записи комплексных чисел:

I Ie j
- показательная форма записи;
I a jb
- алгебраическая форма записи;
I a2 b2
- модуль комплексного числа (длина вектора);
- аргумент комплексного числа (угол вектора);
arctg b
a
a I cos
- действительная (вещественная) часть комплексного числа;
b I sin
- мнимая часть комплексного числа;
I Im
2
- действующее значение тока.
Пример 1:
Для мгновенного значения u (t ) 141sin (314t 30 ) В
определить комплексное значение напряжения.
Пример 2:
Для I 10e
j 60
А
определить мгновенное значение тока.

8. Основные действия над комплексными числами:

A2 A2e j 2 a2 jb2
A1 A1e j 1 a1 jb1
A1 A2 a1 a2 j (b1 b2 )
- сложение (вычитание):
- умножение: A1 A2 A1 A2 e j ( 1 2 ) (a1 jb1 )(a2 jb2 ) a1a2 b1b2 j (a1b2 a2b2 )
- деление:
A1 a1 jb1 (a1 jb1 )(a2 jb2 ) a1a2 b1b2
a2b1 a1b2
j
A2 a2 jb2
a22 b22
a22 b22
a22 b22
A1 A1 j( 1 2 )
e
A2 A2
j a jb
*
- сопряжённое комплексное число: A Ae
AA A2
Комплексное число еj называется оператором поворота, т.к. при умножении
любого числа на еj - вектор поворачивается на комплексной плоскости на
угол .
j 90
e
j
Умножение числа на j поворачивает вектор на
плоскости на 90 против часовой стрелки, если “+” и
по часовой, если “-“.

9.

Элементы R, L, C
в электрической цепи синусоидального тока
u U msin(ωt ψu )
•Активное сопротивление R.
i
R
u
i
u
R
- закон Ома для мгновенных значений тока и напряжения.
Um
i
sin(ωt ψu ),
R
i I m sin( t u ).
I m U m - закон Ома для амплитудных значений.
R
U
I
R - закон Ома для действующих значений.
u i - начальные фазы напряжения и тока.
Если
U
I
R
U Ue
jψ u
, то I Ie
jψ i
U
U
e jψ u .
R
R
+j
0
U
I
u i
+1
- закон Ома для комплексных значений тока и напряжения.

10.

Элементы R, L, C
в электрической цепи синусоидального тока
•Индуктивность L.
i I m sin( t i ) - мгновенное значение тока.
d
di
L
L .
Согласно закону электромагнитной индукции: e
dt
dt
i
По второму закону Кирхгофа: u e.
u
di - закон Ома для мгновенных значений.
e u L
dt
u LIm cos( t i ) LIm sin( t i 90 )
Um Um
- закон Ома для
амплитудных значений.
ωL
xL
- закон Ома для действующих значений.
U m ωLI m I m
U
xL
xL ωL 2pfL - реактивно-индуктивное сопротивление.
U
Начальные фазы напряжения и тока: u i 90 ,
u i 90 .
I
+j
Т.е. в индуктивности напряжение опережает ток на 90 .
jψ u
j (ψi 90 )
j 90 jψi
I
+1
0
U Ue IxL e
IxLe e IjxL.
U
- закон Ома для комплексных значений тока и напряжения.
I
jxL

11.

Элементы R, L, C
в электрической цепи синусоидального тока
•Ёмкость C.
u U msin(ωt ψu ) - мгновенное значение напряжения.
dq
C
q Cu.
, где
Ток – скорость изменения заряда во времени: i
dt
du - закон Ома для мгновенных значений.
u
i C
i
dt
U
I m CU m m ;
i ωCU m cos(ωt ψu ) ωCU m sin( ωt ψu 90 )
1
C
1
1
- реактивно-ёмкостное
x
C
C 2pfC сопротивление.
U
I m m - закон Ома для амплитудных значений.
xC
U - закон Ома для действующих значений.
I
xC
Начальные фазы напряжения и тока: i u 90 ,
+j
U
I
u i 90 .
Т.е. в ёмкости ток опережает напряжения по фазе на 90 .
I Ie
I
U
jxC
jψ i
U j (ψu 90 ) U jψu j 90 U
U
e
e e
j
,
xC
xC
xC
jxC
+1
0
- законом Ома для комплексных значений тока и напряжения.

12.

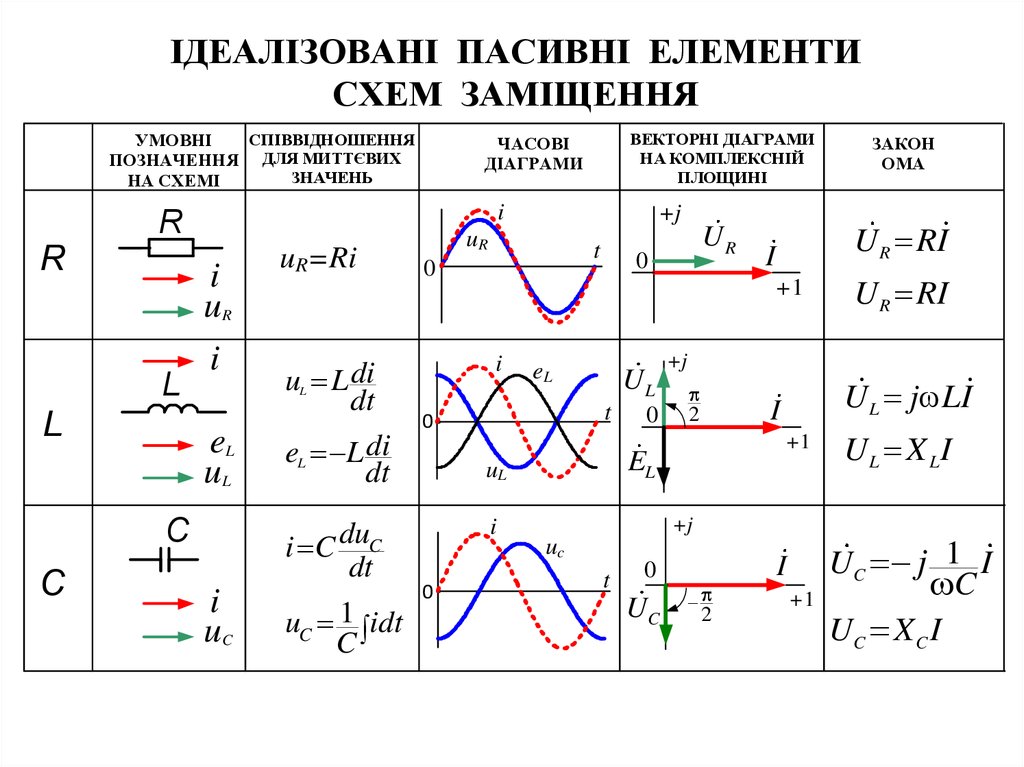
ІДЕАЛІЗОВАНІ ПАСИВНІ ЕЛЕМЕНТИ
СХЕМ ЗАМІЩЕННЯ
СПІВВІДНОШЕННЯ
УМОВНІ
ПОЗНАЧЕННЯ ДЛЯ МИТТЄВИХ
ЗНАЧЕНЬ
НА СХЕМІ
i
R
R
i
uR
L
L
i
uR=Ri
u L di
dt
eL L di
dt
+j
uR
t
0
eL
uL
eL
UL
i
uC
uC 1 idt
C
t
0
0
U R RI
+j
p
2
U L j LI
I
+1
EL
uL
i
0
ЗАКОН
ОМА
U R RI
I
+1
i
i C duC
dt
UR
0
L
C
C
ВЕКТОРНІ ДІАГРАМИ
НА КОМПЛЕКСНІЙ
ПЛОЩИНІ
ЧАСОВІ
ДІАГРАМИ
UL X LI
+j
uc
t
0
UC
p
2
I
+1
UC j 1 I
C
UC X C I

13.

Законы Кирхгофа для цепей синусоидального тока
Первый закон Кирхгофа:
- для мгновенных значений: ik
- для комплексных значений:
Второй закон Кирхгофа:
- для мгновенных значений:
0;
I k 0.
uk ek ;
- для комплексных значений:
U k I k Z k Ek .
Все методы расчета, которые основаны на законах Кирхгофа справедливы и
для цепей синусоидального тока в комплексной форме.
Комплексный (символический) метод расчёта цепей
синусоидального тока
Комплексный метод называется еще символическим методом
расчета., т.к. при расчете используется не истинные токи, напряжения, ЭДС, а
их символы (комплексные числа).
Переход к символам позволяет систему дифферинциальных
уравнений
для
мгновенных
значений
токов
заменить
системой
алгебраических уравнений для комплексов.

14.

Последовательное соединение элементов R, L, C
XL
R
UL
UR
U
I
XC Второй закон Кирхгофа для мгновенных значений
напряжений:
u uR uL uC .
Uc
Второй закон Кирхгофа для комплексных
действующих значений напряжений:
U U R U L UC .
По закону Ома для элементов электрической цепи в комплексной форме:
U R I R;
U L IjxL ;
U C I ( jxC ).
U I R j ( xL xC )].
Z R j ( xL xC ) R jx ze j
где
- комплексное сопротивление цепи.
z R 2 x 2 R 2 ( xL xC )2 - модуль комплексного сопротивления цепи.
x x - угол смещения фаз между
x
arctg arctg L C напряжением и током на входе xC
R
R
xL
I
U
z
U Ue
I
Ie j i , ψi ψu .
Z
ze j
- закон Ома для действующих значений.
Таким образом:
схемы.
j u
z
r

15.

Последовательное соединение элементов R, L, C
Векторная диаграмма: в зависимости от соотношения xL и xC
+j
возможно три состояния цепи:
1.
xL xC x 0 0 u i
+j
UL
2.
+1
0
U
Uc
Uc
Ur
0
I
Ur
3.
U
- активно-индуктивный характер электрической
цепи.
UL
xL xC x 0 0 u i
- активно-ёмкостной характер электрической
цепи.
xL xC x 0 0 u i
- активный характер электрической цепи.
Резонанс напряжений.
I
+1

16.

Последовательное соединение элементов R, L, C
Резонанс напряжений
Резонансом называется режим работы участка цепи с реактивными
элементами, в котором ток и напряжение совпадают по фазе. Сопротивление
электрической цепи является чисто активным.
Условие резонанса напряжений
ω0 L
1
;
ω0 C
ω0
1
LC
xL xC ; соответственно x xL xC 0.
резонансная круговая частота.
Резонанс может быть достигнут изменением частоты, индуктивности или емкости.
Z R j ( xL xC ) R;
I
U
,
R
z R min,
I max .
При резонансе напряжений напряжение на реактивных элементах может
превышать входное. Добротность контура - Q:
Волновое сопротивление контура:
L
C
U L IxL xL
Q
U
IR
R

17.

Последовательное соединение элементов R, L, C
X
Резонанс напряжений
X
C
L
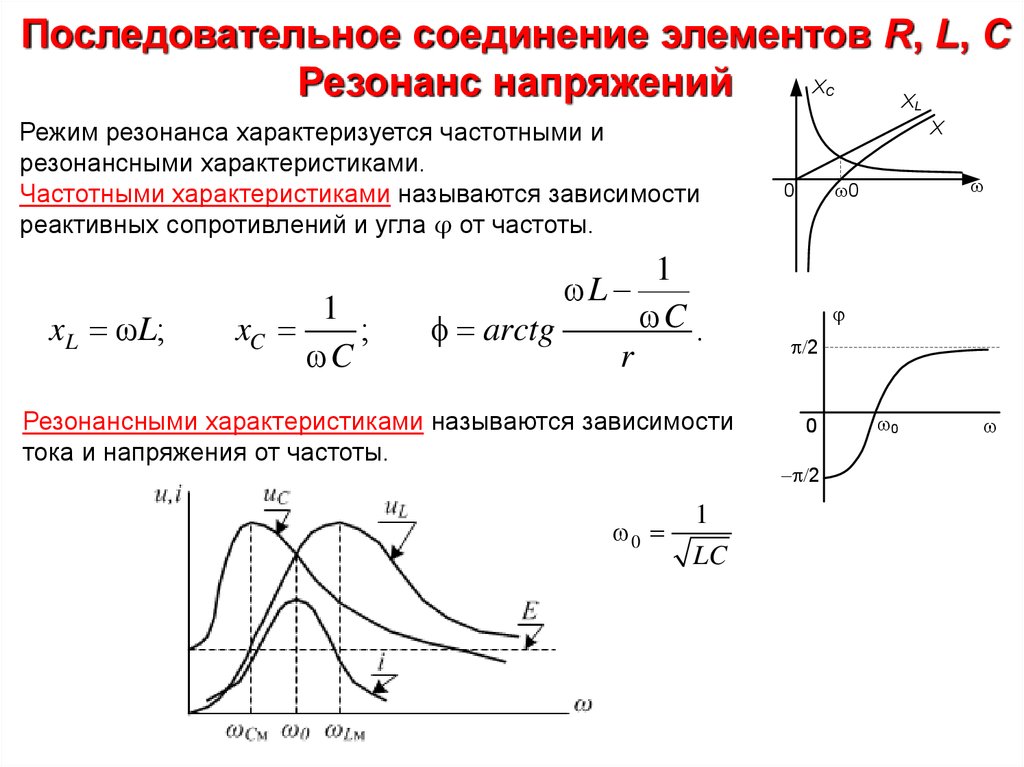
Режим резонанса характеризуется частотными и
резонансными характеристиками.
Частотными характеристиками называются зависимости
реактивных сопротивлений и угла φ от частоты.
xL ωL;
xC
1
;
C
arctg
L
r
1
C .
Резонансными характеристиками называются зависимости
тока и напряжения от частоты.
0
1
LC
X
0
0
p/2
0
p/2
0

18.

Комплексный метод анализа цепей
синусоидального тока
1. Выбрать положительное направление токов во всех ветвях, указав их
стрелками на схеме.
2. Представить исходные данные о параметрах всех источников и элементов
цепи в комплексной форме: J(t)→ J , e(t) → E и R, XL, XC.
e(t ) Emsin(ωt ψe ) →
Z R;
E
Em
2
e
j e
Z jxL jωL j 2pfL;
.
Z - jx
C
1
1
j
.
j C
2pfC
3. Пользуясь законами Ома и Кирхгофа в комплексной форме, составить
систему уравнений и определить комплексные значения токов во всех ветвях
схемы.
4. Перейти от комплексных значений токов (напряжений) к их мгновенным
значениям i(t) или u(t).

19.

Расчёт электрических цепей
синусоидального тока
Задача 1. Определить мгновенное значение тока, если параметры элементов:
XL
R
U
UL
UR
I
Решение.
XC
Uc
R=3 Ом, XL=4 Ом, XC=8 Ом.
Приложенное напряжение равно:
u (t ) 141 sin(314t 30 ) B.

20.

Мощности в цепях переменного тока
Мгновенная мощность p –
произведение мгновенных значений
напряжения и тока:
p ui
u U msin(ωt ψu ), i I m sin( t i ).
Активная мощность P – среднее значение мгновенной мощности за период.
Характеризует скорость преобразования электроэнергии в другие её виды:
1T
P pdt ,
T0
P UI cos , Вт
S UI , BA
Q UI sin , вар.
Максимальное значение активной мощности, которое может быть получено
при данных значениях напряжения и тока, называется полной мощностью S.
Реактивная мощность Q – это мощность обмена энергии между источником и
реактивным элементом.
2
2
S
P
Q
Для удобства и упрощения вычислений вводится
понятие комплексной мощности - произведение
комплексного, действующего значения напряжения
на сопряженный комплекс тока:
~
S U I Ue j u Ie j i UIe j Se j S cos jS sin P jQ.

21.

Расчёт электрических цепей
синусоидального тока
Задача 2. Определить активную, реактивную и полную мощности в цепи
переменного тока, если
u (t ) 282 cos( t 15 ) B
i (t ) 5 2 sin( t 60 ) А.
и

22.

Параллельное соединение элементов R, L, C
Согласно первому закону Кирхгофа и закону Ома в комплексной форме:
R
U
Ir
I I R I L I C ;
U I R R;
U I L jxL ;
U I C ( jx ).
C
XL
XC
IL
IC
IC
U
U ( jbC ).
jxC
U
I R U g;
R
IL
Y
U
U ( jbL );
jxL
1
Z
- комплексная проводимость
I U Y
I Uy
I U g j bL bC U Y
Y g j (bL bC ) g jb ye j
- закон Ома для комплексных значений;
- закон Ома для действующих значений.

23.

Параллельное соединение элементов R, L, C
g
Y g j (bL bC ) g jb ye j
bL
y
bC
bL
bC
b bL bC
g
1
xC
1
xL
1
- активная проводимость;
R
- реактивно-индуктивная проводимость;
- реактивно-ёмкостная проводимость.
- реактивная проводимость;
y g 2 b2 g 2 (bL bC )2
arctg
b b
b
arctg L C
g
g
- модуль полной проводимости;
- аргумент полной проводимости;

24.

Параллельное соединение элементов R, L, C
Векторная диаграмма: в зависимости от соотношения параметров bL и bC
возможны три характера цепи:
1.
bL bC b 0 0 u i
U
Ir
.
- активно-индуктивный характер электрической
цепи.
+j
I
Ic
0
Ir
0
+j
0
0
IL
2. bL bC b 0, 0 u i
+1
+1
I
U
.
u
Ic
IL
- активно-ёмкостной характер электрической
цепи.
+j
3. bL bC b 0, 0 u i
I = Ir
- активный характер электрической цепи.
Резонанс токов.
U
.
Ic
+1
0
IL

25.

I
Резонанс токов
a
I1
U
I2
R1
R2
L
C
b
Согласно первому закону Кирхгофа:
I I1 I 2
Y1
( R jxL ) R1 jxL
1
1
1
;
2
2
Z 1 R1 jxL ( R1 jxL ) R1 xL
Y1
R1
xL
1
j
g1 jbL ;
2
2
2
2
Z 1 R1 xL
R1 xL
I 1 U Y1 U ( g1 jbL ) I1a jI1 p ;
Y2
( R jxС ) R2 jxС
xС
R2
1
1
2
j
g 2 jbС ;
2
2
2
2
2
2
Z 2 R2 jxС ( R2 jxС ) R2 xС R2 xС
R2 xС
I 2 U Y2 U ( g 2 jbС ) I 2 a jI 2 p ;
Y Y1 Y2 ( g1 g 2 ) j (bL bС ) g jb
I U Y U ( g jb).
- полная проводимость;

26.

I
a
Резонанс токов
I2
I1
U
R1
R2
L
C
I U Y U ( g jb).
bL bC
Условие резонанса токов:
bL
xL
R12
xL2
;
b
При резонансе токов входной ток I min
определяется только активной проводимостью:
bC
xC
;
R2 xC2
2
+j
I2
I Uy U ( g1 g 2 ) 2 (bL bC ) 2 Ug
IR I
0
b
bL
bC
I1
0 u i
C
b 0.
Частотные резонансные характеристики
проводимостей реактивных элементов.
U
+1

27.

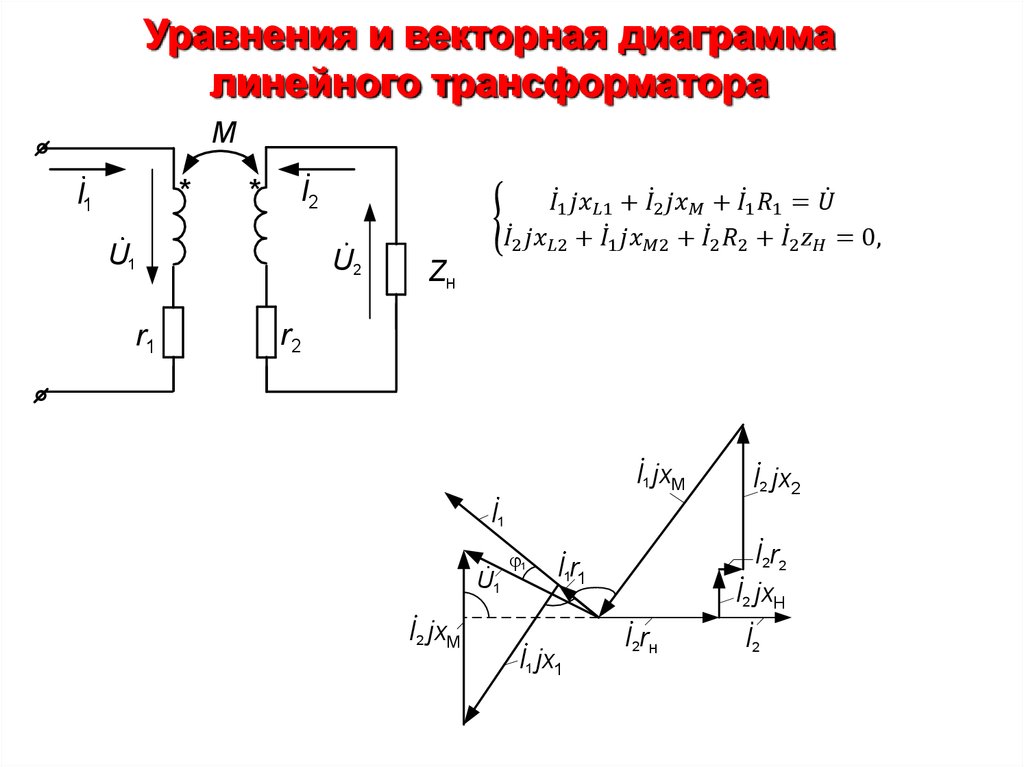
Электрические цепи
с магнитно-связанными элементами
Когда изменение тока в одном из элементов цепи приводит к появлению ЭДС в
другом элементе цепи, говорят, что эти два элемента индуктивно связаны, а
возникающую ЭДС называют ЭДС взаимной индукции. Степень индуктивной
связи элементов характеризуется коэффициентом связи (kc).
Ф12
Ф21
Ф11
*
I 1
Ф22 *
I 2