Electro_2_ОЦ

1. Электротехника 2 Однофазные цепи переменного тока

Воршевский Александр Алексеевич
Зав. кафедрой Э и ЭОС

2.

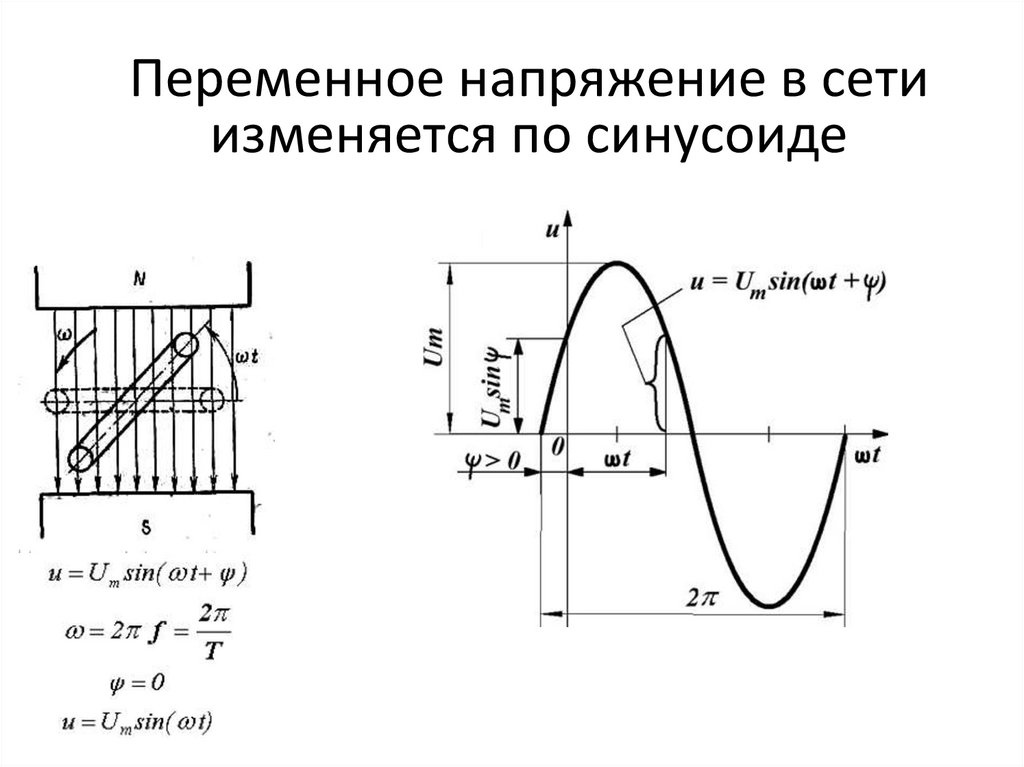
Переменное напряжение в сети
изменяется по синусоиде

3.

Обозначения электрических величин
Мгновенное значение напряжения и тока:
u=u(t)=Umsin (ωt+ψu)
i=i(t)=Imsin (ωt+ψi)
Амплитудное значение напряжения есть максимальное по модулю значение мгновенного
напряжения за весь период колебаний:
Um=max(|u|)
Im=max(|i|)
Среднеквадратическое значение напряжения или действующее значение напряжения
Для переменного синусоидального напряжения U=Um/√2=0,707 Um
Для переменного синусоидального тока действующее значение

4.

Обозначения основных величин
Значение напряжения
u – мгновенное
Um – амплитудное
U – действующее, U – комплексное
Значение тока
i – мгновенное
Im – амплитудное
I – действующее, I – комплексное
Значение ЭДС
e – мгновенное
Em – амплитудное
E – действующее, E – комплексное

5.

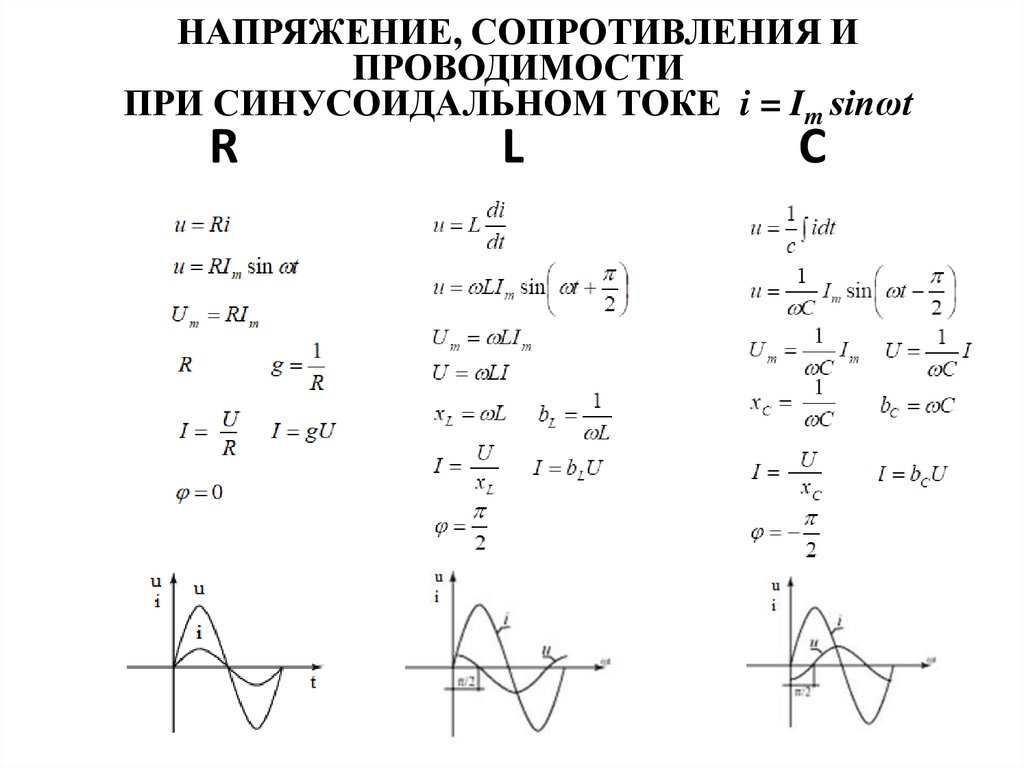
НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЯ И
ПРОВОДИМОСТИ
ПРИ СИНУСОИДАЛЬНОМ ТОКЕ i = Im sinωt
R
L
C

6.

НАПРЯЖЕНИЯ, СОПРОТИВЛЕНИЯ И
ПРОВОДИМОСТИ
ПРИ СИНУСОИДАЛЬНОМ ТОКЕ i = Im sinωt
R
L
C
Как же рассчитывать токи и напряжения в цепи
с конденсаторами и катушками индуктивности?
Решать дифференциальные уравнения?

7.

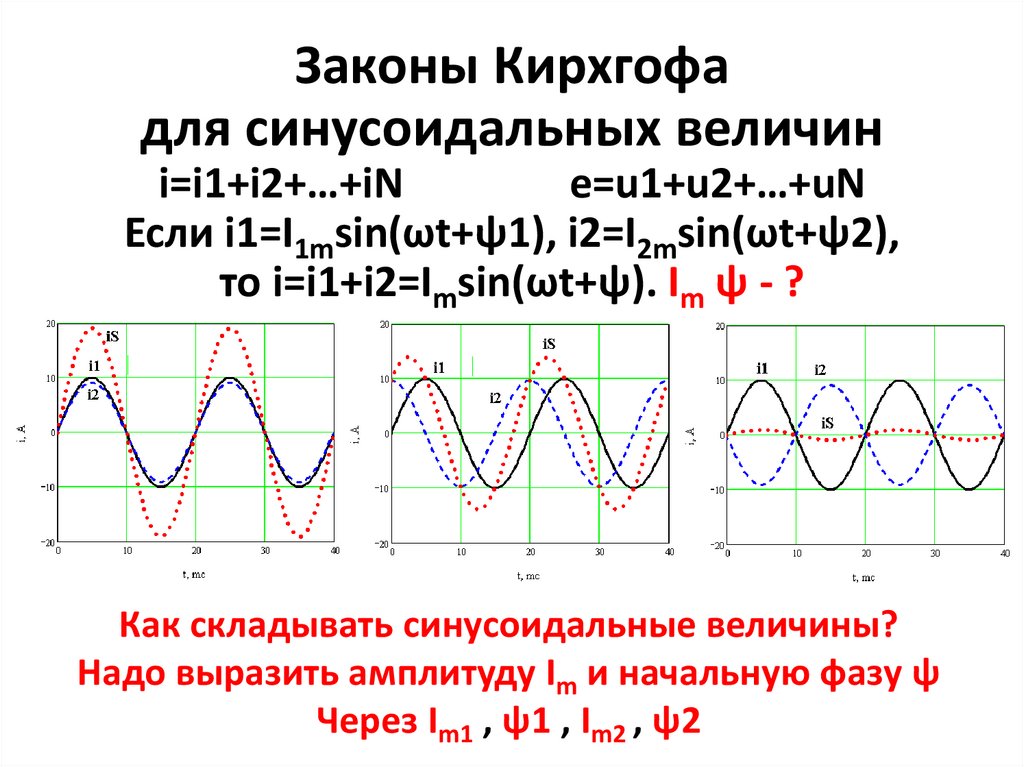
Законы Кирхгофа
для синусоидальных величин
i=i1+i2+…+iN
e=u1+u2+…+uN
Если i1=I1msin(ωt+ψ1), i2=I2msin(ωt+ψ2),
то i=i1+i2=Imsin(ωt+ψ). Im ψ - ?
Как складывать синусоидальные величины?
Надо выразить амплитуду Im и начальную фазу ψ
Через Im1 , ψ1 , Im2 , ψ2

8.

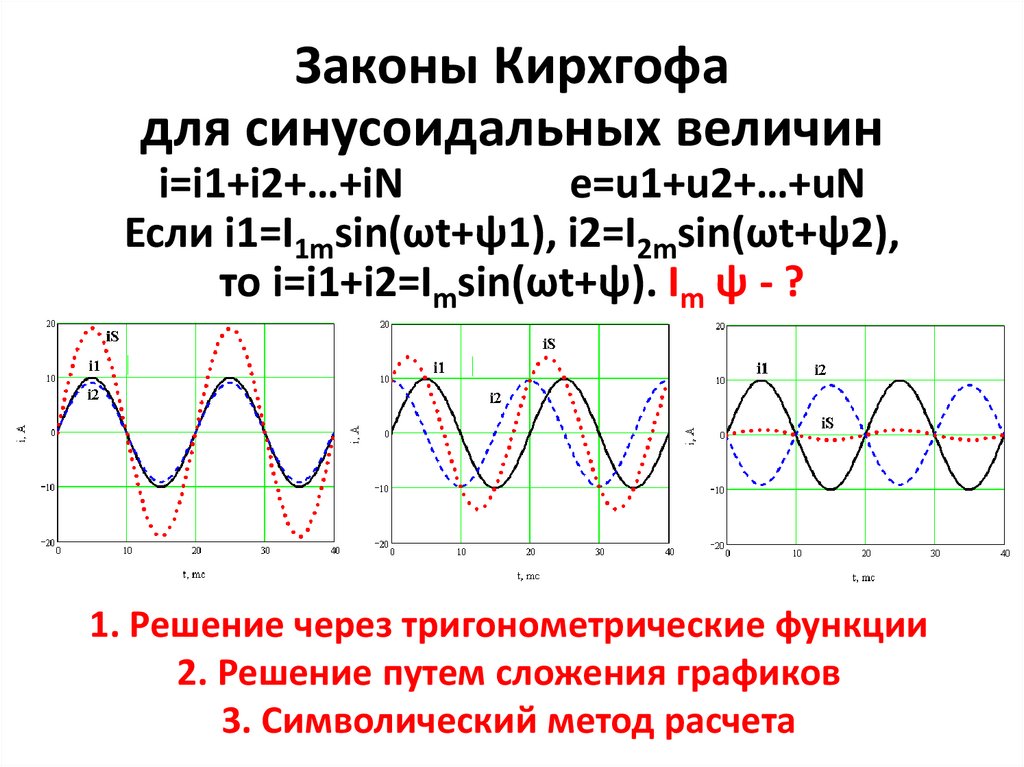
Законы Кирхгофа
для синусоидальных величин
i=i1+i2+…+iN
e=u1+u2+…+uN
Если i1=I1msin(ωt+ψ1), i2=I2msin(ωt+ψ2),
то i=i1+i2=Imsin(ωt+ψ). Im ψ - ?
1. Решение через тригонометрические функции
2. Решение путем сложения графиков
3. Символический метод расчета

9.

Представление синусоидальных величин в
комплексной форме
Тригонометрическая запись
u=Umsin(ωt+ψ),
параметры Um ψu
вместо Um удобно U=Um/√2

10.

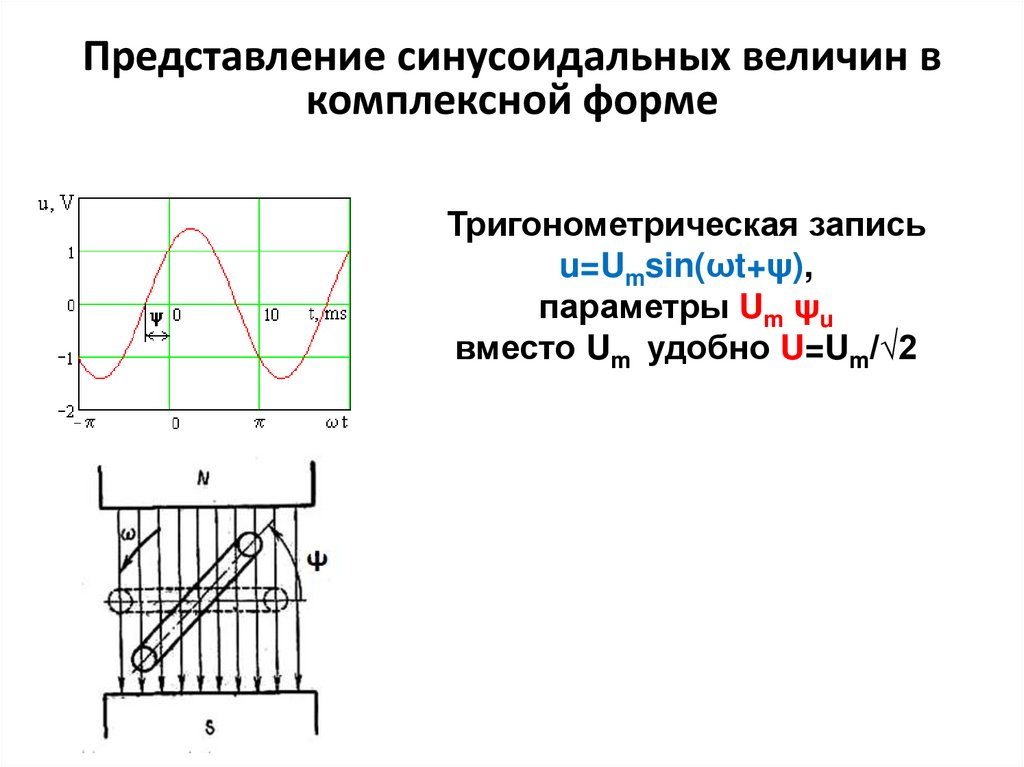
Представление синусоидальных величин в
комплексной форме
Тригонометрическая запись
u=Umsin(ωt+ψ),
параметры Um ψu
вместо Um удобно U=Um/√2

11.

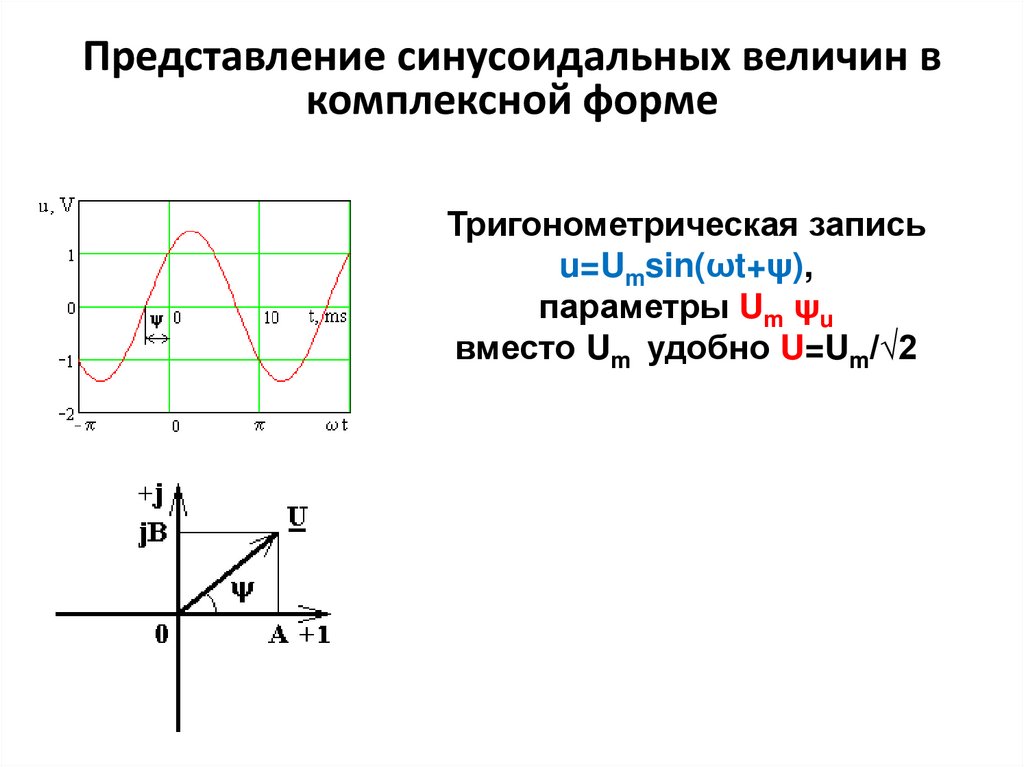
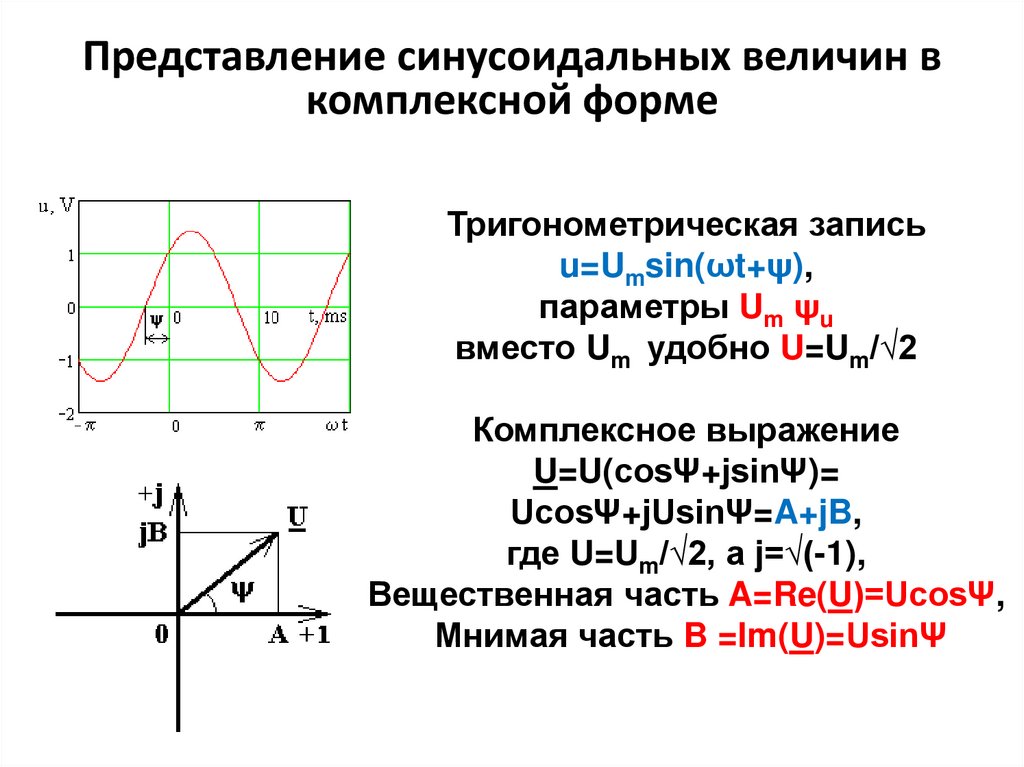
Представление синусоидальных величин в
комплексной форме
Тригонометрическая запись
u=Umsin(ωt+ψ),
параметры Um ψu
вместо Um удобно U=Um/√2
Комплексное выражение
U=U(cosΨ+jsinΨ)=
UcosΨ+jUsinΨ=A+jB,
где U=Um/√2, а j=√(-1),
Вещественная часть A=Re(U)=UcosΨ,
Мнимая часть B =Im(U)=UsinΨ

12.

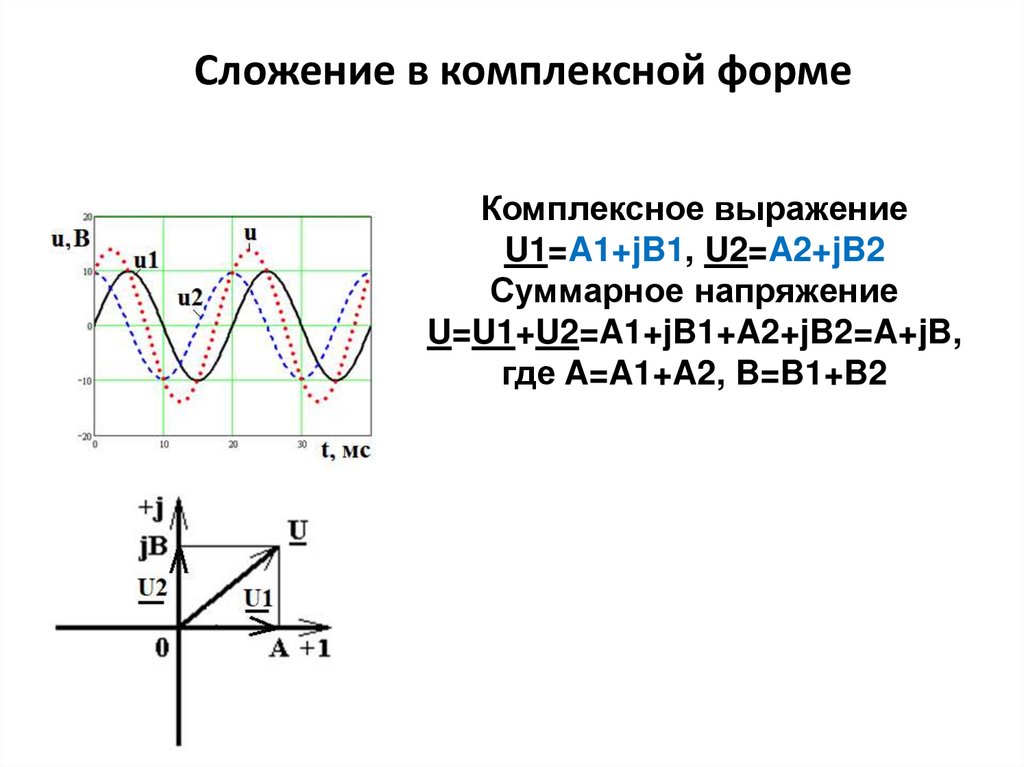
Сложение в комплексной форме
Комплексное выражение
U1=A1+jB1, U2=A2+jB2
Суммарное напряжение
U=U1+U2=A1+jB1+A2+jB2=A+jB,
где A=A1+A2, B=B1+B2

13.

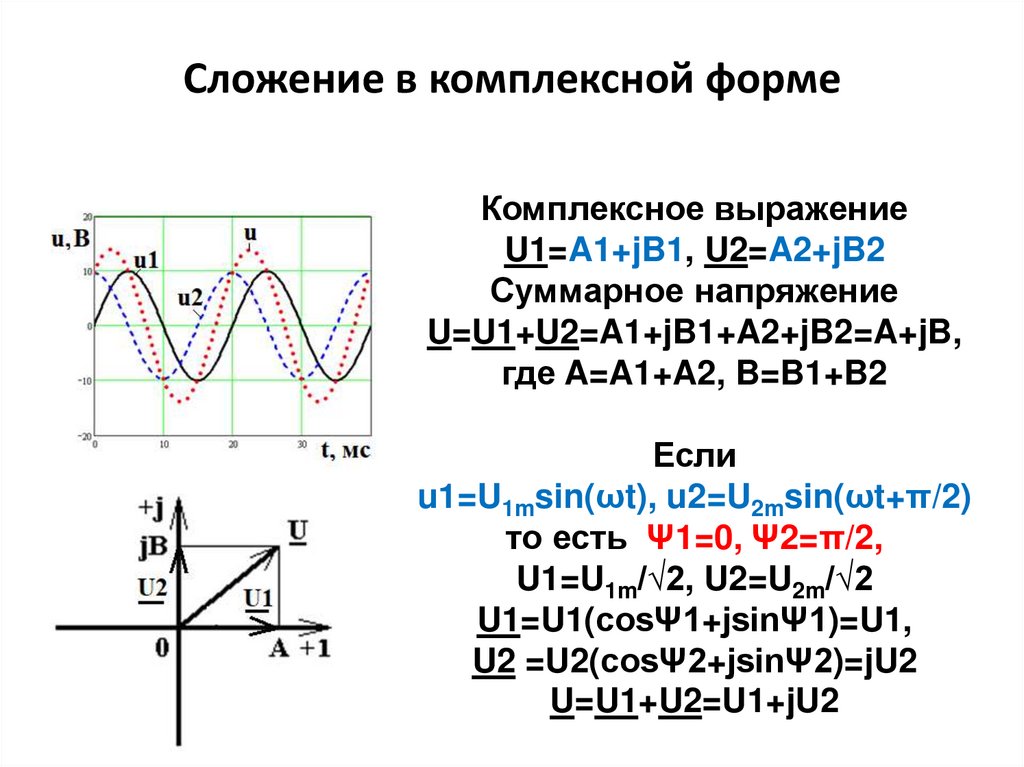
Сложение в комплексной форме
Комплексное выражение
U1=A1+jB1, U2=A2+jB2
Суммарное напряжение
U=U1+U2=A1+jB1+A2+jB2=A+jB,
где A=A1+A2, B=B1+B2
Если
u1=U1msin(ωt), u2=U2msin(ωt+π/2)
то есть Ψ1=0, Ψ2=π/2,
U1=U1m/√2, U2=U2m/√2
U1=U1(cosΨ1+jsinΨ1)=U1,
U2 =U2(cosΨ2+jsinΨ2)=jU2
U=U1+U2=U1+jU2

14.

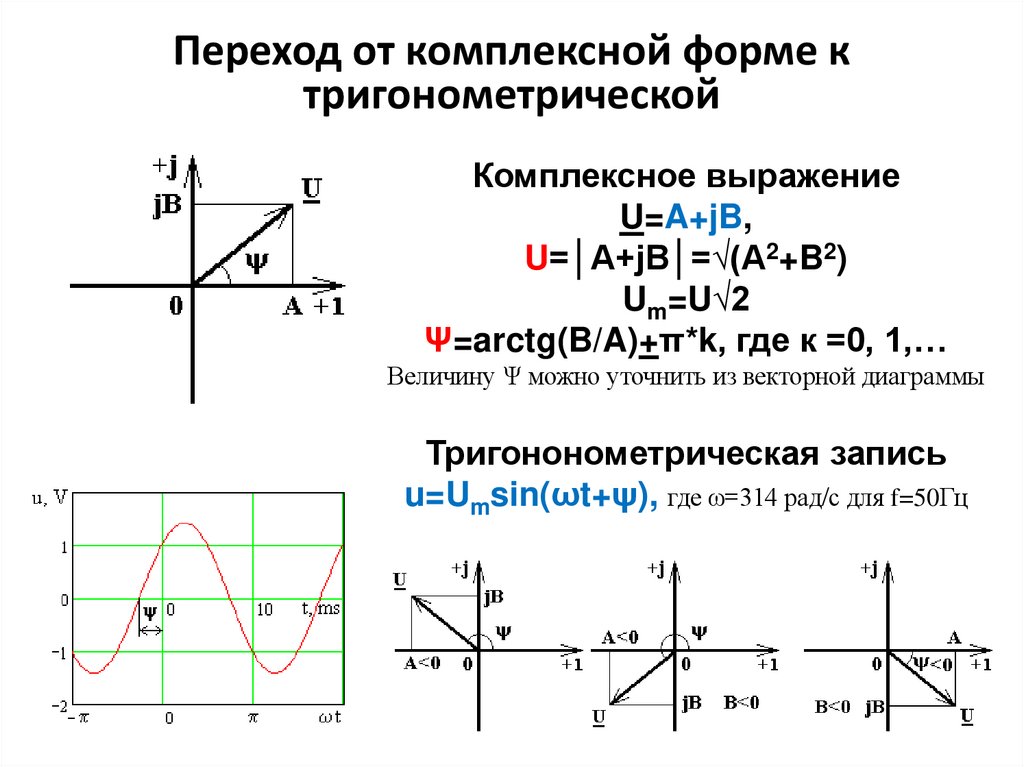
Переход от комплексной форме к
тригонометрической
Комплексное выражение
U=A+jB,
U=│А+jB│=√(A2+B2)
Um=U√2
Ψ=arctg(B/A)+π*k, где к =0, 1,…
Величину Ψ можно уточнить из векторной диаграммы
Тригононометрическая запись
u=Umsin(ωt+ψ), где ω=314 рад/с для f=50Гц

15.

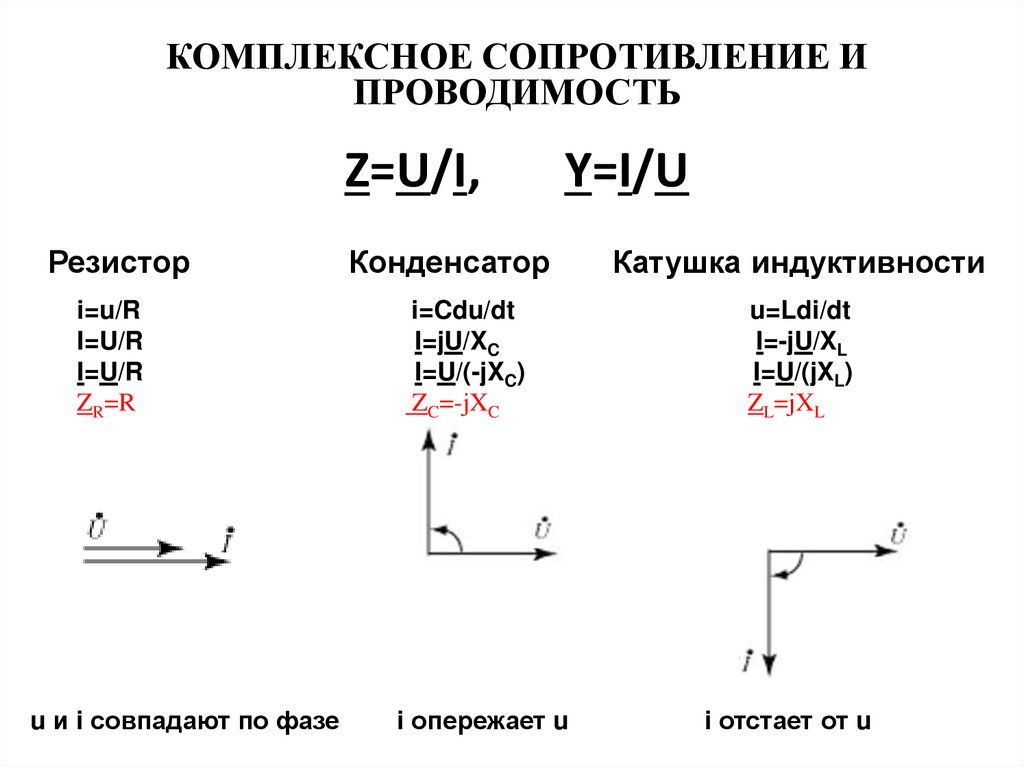
КОМПЛЕКСНОЕ СОПРОТИВЛЕНИЕ И
ПРОВОДИМОСТЬ
Z=U/I,
Резистор
i=u/R
I=U/R
I=U/R
ZR=R
u и i совпадают по фазе
Y=I/U
Конденсатор
Катушка индуктивности
i=Cdu/dt
I=jU/XC
I=U/(-jXC)
ZC=-jXC
u=Ldi/dt
I=-jU/XL
I=U/(jXL)
ZL=jXL
i опережает u
i отстает от u

16.

КОМПЛЕКСНЫЕ СОПРОТИВЛЕНИЯ И
ПРОВОДИМОСТИ ОСНОВНЫХ ЭЛЕМЕНТОВ
R
L
C
ВАЖНО ЗНАТЬ! Резистор ZR=R, конденсатор ZC=-jXC,
идеальная катушка индуктивности ZL=jXL, реальная катушка ZK=RK+jXL

17.

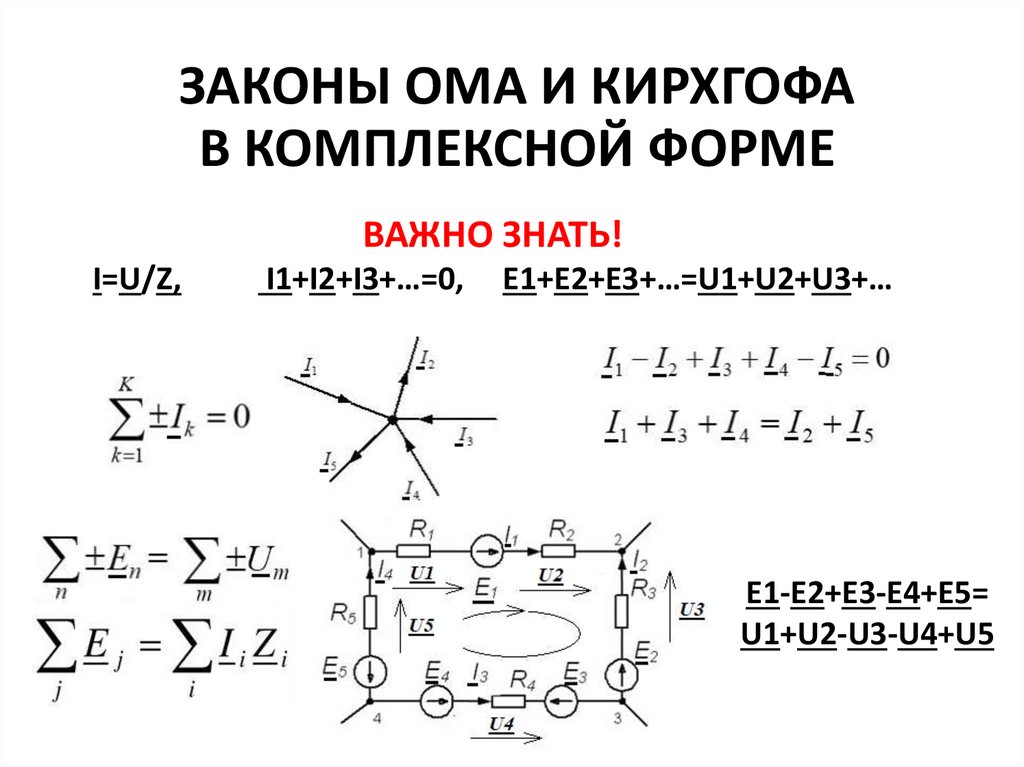
ЗАКОНЫ ОМА И КИРХГОФА
В КОМПЛЕКСНОЙ ФОРМЕ
ВАЖНО ЗНАТЬ!
I=U/Z,
I1+I2+I3+…=0,
E1+E2+E3+…=U1+U2+U3+…
E1-E2+E3-E4+E5=
U1+U2-U3-U4+U5

18.

Соединение элементов
ВАЖНО ЗНАТЬ!
При последовательном соединении
Z= Z1+Z2
Z= Z1+Z2+Z3+Z4+…+ZN
При параллельном соединении
Z= Z1 Z2/(Z1+Z2)
Z=1/(1/Z1+1/Z2+…+1/ZN)

19.

МОЩНОСТЬ
Активная мощность P=UIcosφ характеризует
энергию, выделяемую в цепи.
Реактивная мощность Q=UIsinφ характеризует обмен
энергией между цепью и источником электроэнергии.
Полная мощность - просто произведение S=UI.
Коэффициент мощности cosφ=P/S

20.

МОЩНОСТЬ В КОМПЛЕКСНОЙ
ФОРМЕ
ВАЖНО ЗНАТЬ!
комплексная мощность S=U I*=P+jQ
где U - комплексное напряжение на конкретной цепи,
I*- сопряженный комплексный ток цепи.
(Сопряженное число - это число с противоположным знаком перед мнимой частью).
Вещественная часть комплексной мощности – это
активная мощность P=UIcosφ, а мнимая – это
реактивная мощность Q=UIsinφ.
Модуль комплексной мощности – это и есть полная
мощность S=UI. Модуль S=│P+jQ│=√(P2+Q2)
Коэффициент мощности cosφ=P/S

21.

Алгоритм расчета
цепей переменного тока
1) Обозначить на схеме все разные напряжения и токи.
Токи обозначаются стрелками на соединительных линиях схемы (на проводниках). Напряжение обозначается
между разными точками схемы длинной стрелкой, начинающейся от одного узла схемы и оканчивающейся у
другого узла схемы.
2) Выразить в комплексной форме заданную ЭДС, напряжение, ток.
u(t)=Umsin(ωt+Ψ) представляется в комплексной форме по формуле U=U(cosΨ+jsinΨ),
где U=Um/√2, а j=√(-1). Можно задаться начальной фазой только одной величины.
3) Выразить в комплексной форме сопротивления элементов.
Резистор ZR=R, конденсатор ZC=-jXC, идеальная катушка индуктивности ZL=jXL
4) Составить систему уравнений, связывающих ЭДС, напряжения,
токи и сопротивления элементов в схеме.
Используются законы Ома, Кирхгофа в комплексной форме.
5) Решить систему уравнений относительно неизвестных величин.
В результате получают комплексные значения неизвестных величин. Можно построить векторную диаграмму на
комплексной плоскости.
6) Найти модули неизвестных величин как корень квадратный из суммы квадратов
вещественной и мнимой частей комплексного выражения величины. Можно также найти начальные фазы величин
и представить величины в тригонометрической форме или построить график зависимости величины от времени.

22.

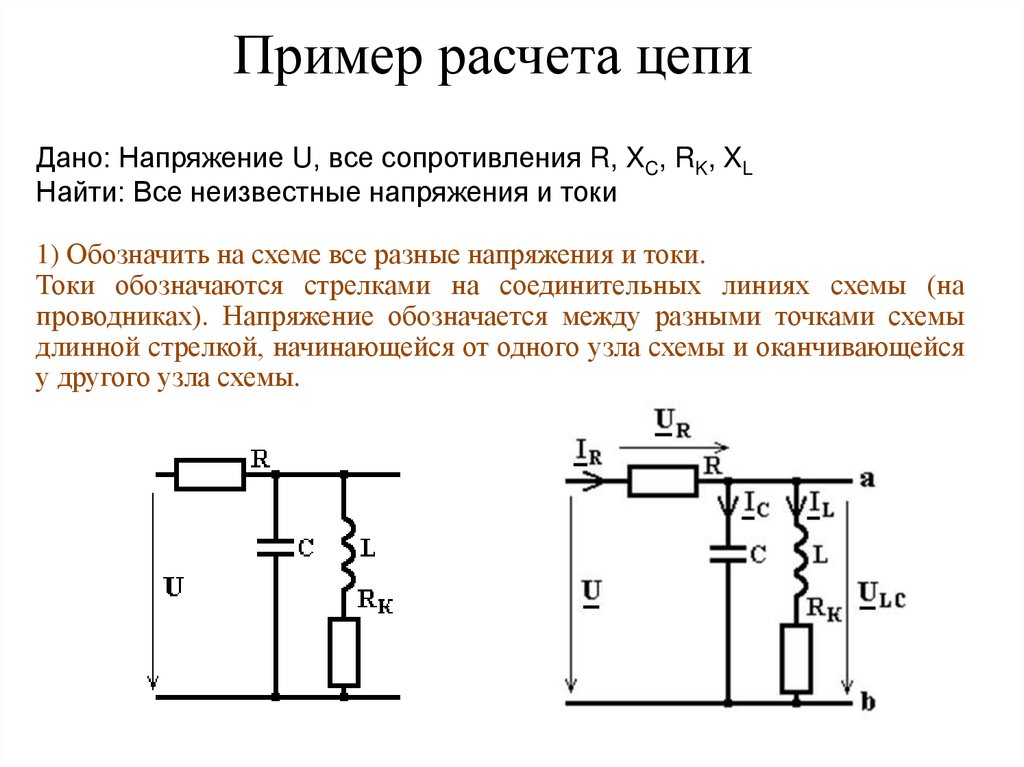
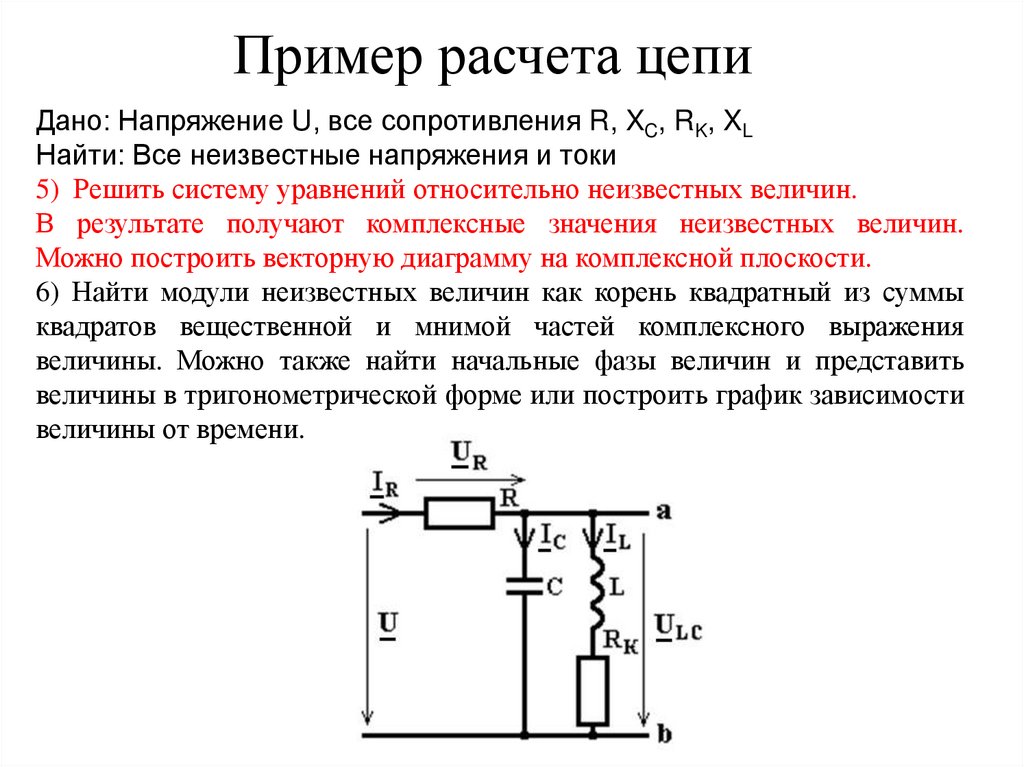
Пример расчета цепи
Дано: Напряжение U, все сопротивления R, XC, RK, XL
Найти: Все неизвестные напряжения и токи
1) Обозначить на схеме все разные напряжения и токи.
Токи обозначаются стрелками на соединительных линиях схемы (на
проводниках). Напряжение обозначается между разными точками схемы
длинной стрелкой, начинающейся от одного узла схемы и оканчивающейся
у другого узла схемы.

23.

Пример расчета цепи
Дано: Напряжение U, все сопротивления R, XC, RK, XL
Найти: Все неизвестные напряжения и токи
2) Выразить в комплексной форме заданную ЭДС, напряжение, ток.
u(t)=Umsin(ωt+Ψ) представляется в комплексной форме по формуле
U=U(cosΨ+jsinΨ),
где U=Um/√2, а j=√(-1). Можно задаться начальной фазой только одной
величины. Если положить Ψ=0, то U=U, т.к. cos0=1, sin0=0. Все остальные
напряжения и токи будут иметь начальные фазы, рассчитанные по формулам. Ими
задаваться нельзя. Комплексные напряжения, токи, ЭДС подчеркиваются снизу. Не
подчеркнутое напряжение U означает действующее значение или модуль |U|.

24.

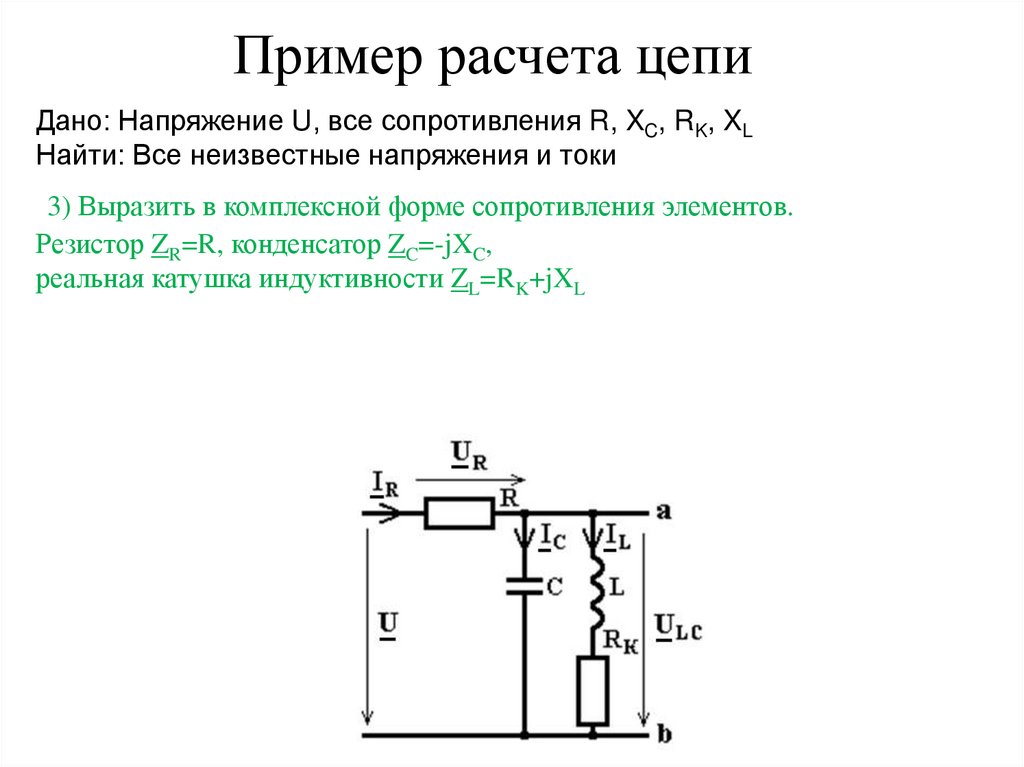
Пример расчета цепи
Дано: Напряжение U, все сопротивления R, XC, RK, XL
Найти: Все неизвестные напряжения и токи
3) Выразить в комплексной форме сопротивления элементов.
Резистор ZR=R, конденсатор ZC=-jXC,
реальная катушка индуктивности ZL=RK+jXL

25.

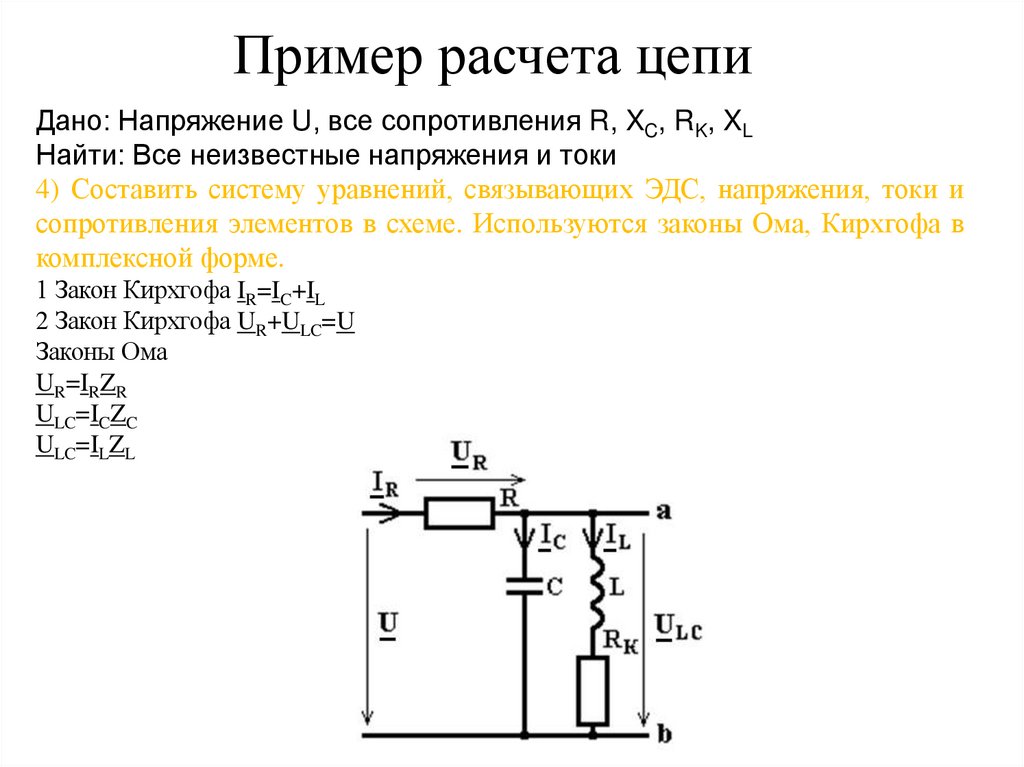
Пример расчета цепи
Дано: Напряжение U, все сопротивления R, XC, RK, XL
Найти: Все неизвестные напряжения и токи
4) Составить систему уравнений, связывающих ЭДС, напряжения, токи и
сопротивления элементов в схеме. Используются законы Ома, Кирхгофа в
комплексной форме.
1 Закон Кирхгофа IR=IC+IL
2 Закон Кирхгофа UR+ULC=U
Законы Ома
UR=IRZR
ULC=ICZC
ULC=ILZL

26.

Пример расчета цепи
Дано: Напряжение U, все сопротивления R, XC, RK, XL
Найти: Все неизвестные напряжения и токи
5) Решить систему уравнений относительно неизвестных величин.
В результате получают комплексные значения неизвестных величин.
Можно построить векторную диаграмму на комплексной плоскости.
6) Найти модули неизвестных величин как корень квадратный из суммы
квадратов вещественной и мнимой частей комплексного выражения
величины. Можно также найти начальные фазы величин и представить
величины в тригонометрической форме или построить график зависимости
величины от времени.

27.

Пример расчета цепи
Дано: Напряжение U, все сопротивления R, XC, RK, XL
Найти: Все неизвестные напряжения и токи
5) Решить систему уравнений относительно неизвестных величин.
В результате получают комплексные значения неизвестных величин.
Можно построить векторную диаграмму на комплексной плоскости.
Решаем относительно неизвестных IR, IC, IL, UR, ULC
Можно также находить решение через расчет сопротивлений
При последовательном соединении Z= Z1+Z2 (только в комплексной форме!)
При параллельном соединении Z= Z1 Z2/(Z1+Z2) (только в комплексной форме!)
Общее сопротивление всей схемы
ZЭ= ZR+ZLC, где ZLC= ZC ZK/(ZC+ZK).
Тогда ZЭ= ZR+ ZC ZK/(ZC+ZK)
Входной ток всей схемы IR=U/ZЭ
Напряжения на элементах:
UR=IRZR
ULC=IRZLC
Токи:
IC=ULC/ZC
IL=ULC/ZL

28.

6) Найти модули неизвестных величин как корень квадратный из суммы
квадратов вещественной и мнимой частей комплексного выражения
величины. │А+jB│=√(A2+B2).
Полезные приемы работы с комплексными числами:
Надо не забывать, что j2=-1
Избавиться от мнимых величин в знаменателе можно умножив числитель и
знаменатель на сопряженное знаменателю
(A+jB)/(C+jD)=(A+jB)(C-jD)/(C2+D2)
Сопряженное число - это число с противоположным знаком перед мнимой частью.
Расчет мощности цепи или ее части:
комплексная мощность S=U I*=P+jQ
где U - комплексное напряжение на конкретной цепи или ее части,
I*- сопряженный комплексный ток цепи или через ее часть.
Вещественная часть комплексной мощности это активная мощность P[Вт],
а мнимая – это реактивная мощность Q [ВАр].
Модуль комплексной мощности – это полная мощность S =√(P2+Q2) [ВА]

29.

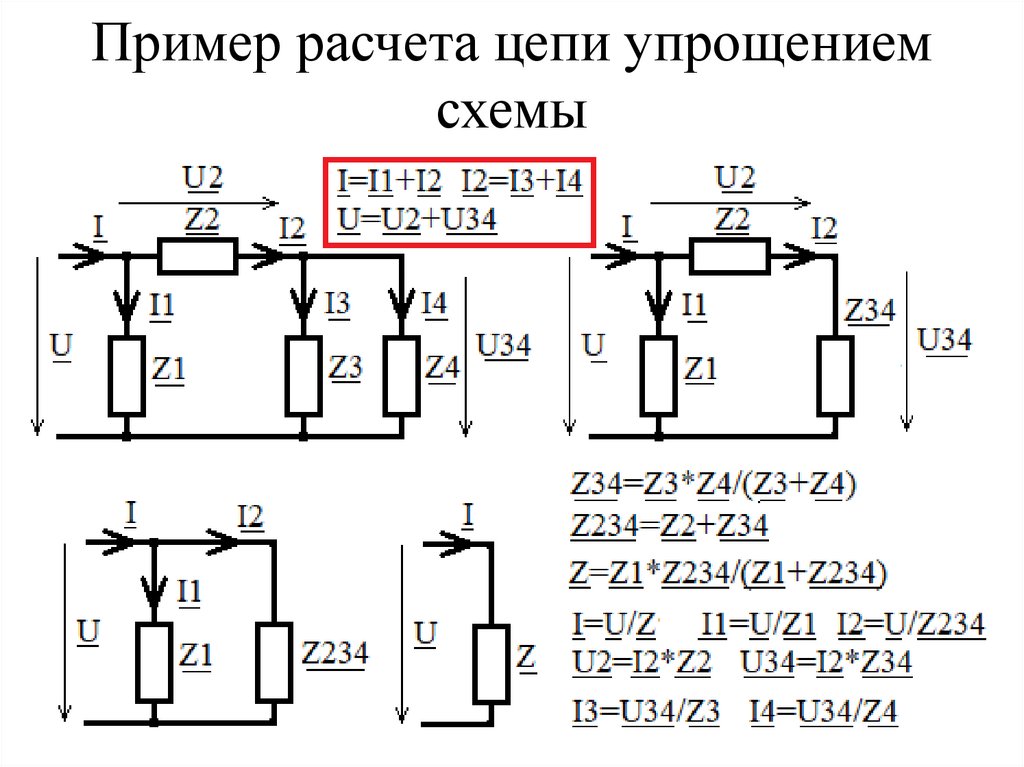
Пример расчета цепи упрощением
схемы

30.

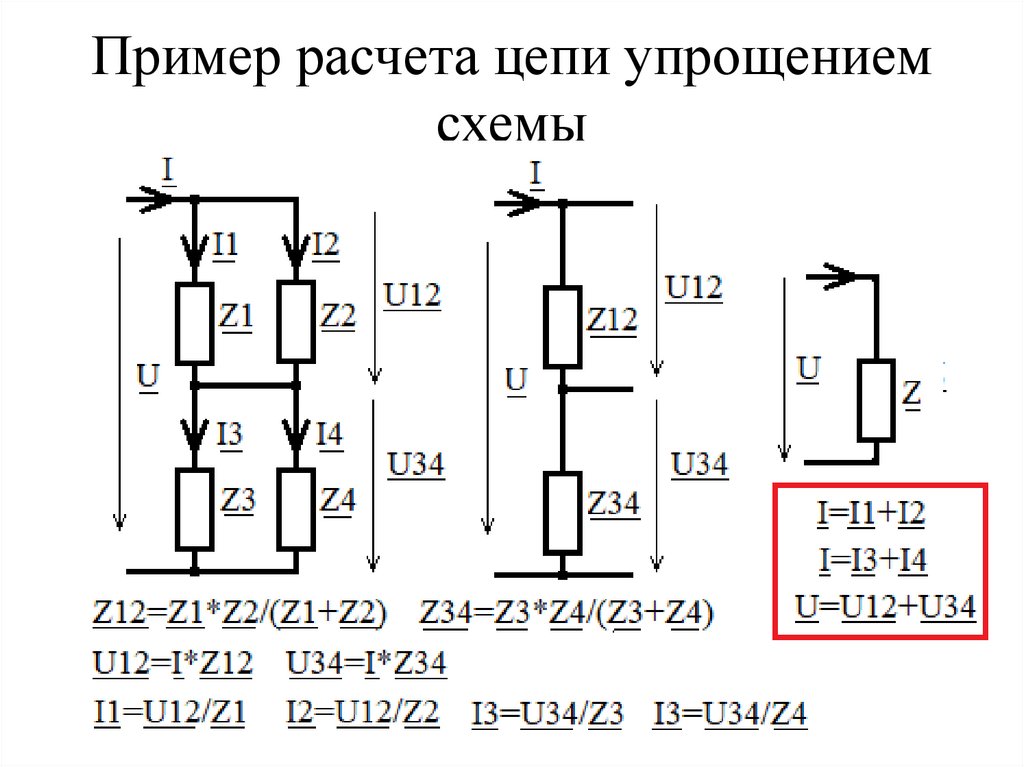
Пример расчета цепи упрощением
схемы

31.

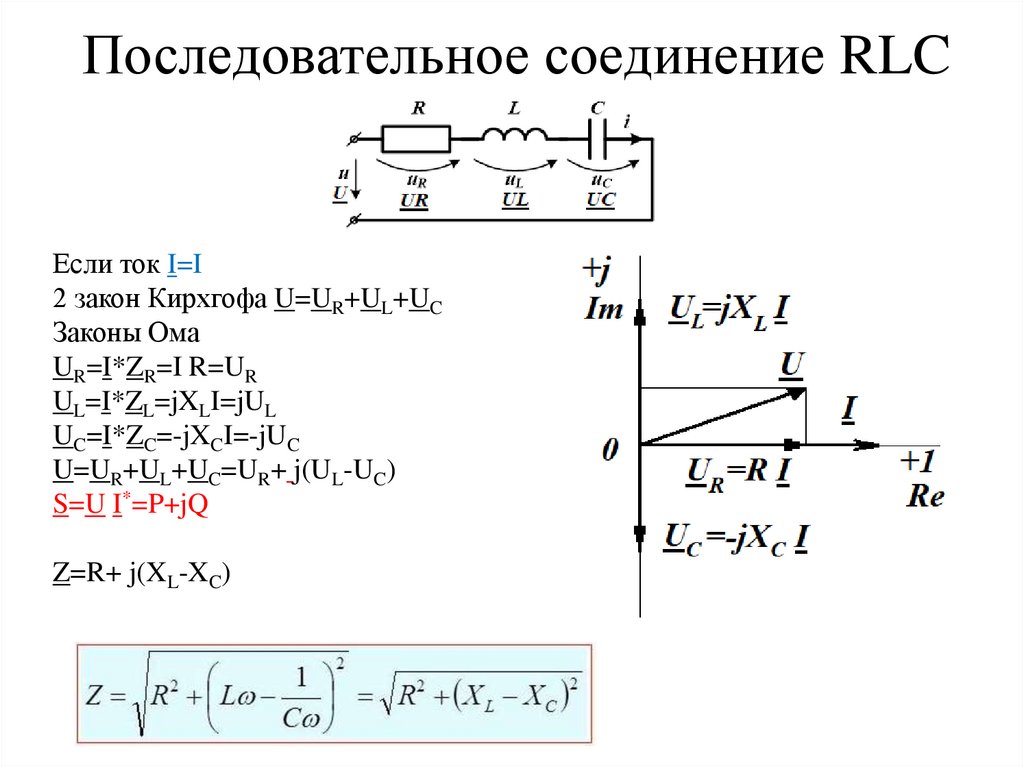
Последовательное соединение RLC
Дано: Напряжение U или ток I, все сопротивления R, XC, XL
Найти: Все разные напряжения и токи
Ток только один - I. Напряжений 4 - U, UR, UL, UC
В комплексной форме записываем все величины.
Если начальная фаза тока Ψ=0, то I=I
Резистор ZR=R, конденсатор ZC=-jXC, катушка индуктивности ZL=+jXL
2 закон Кирхгофа U=UR+UL+UC
Законы Ома UR=I*ZR, Ul=I*Zl, UC=I*ZC,
Подставляем Выражения для законов Ома в формулу закона Кирхгофа
U=UR+UL+UC=I*ZR+I*ZL+I*ZC=I*(ZR+ZL+ZC)=I*(R+ j(XL-XC))
Выражение доказывает, что при последовательном соединении
комплексные сопротивления складываются Z=ZR+ZL+ZC
Если дано напряжение, то ток находится I=U/(ZR+ZL+ZC)=U/(R+ j(XL-XC))
Если дан или расcчитан ток, то U=I*(ZR+ZL+ZC), UR=I*ZR, Ul=I*Zl, UC=I*ZC

32.

Последовательное соединение RLC
Если ток I=I
2 закон Кирхгофа U=UR+UL+UC
Законы Ома
UR=I*ZR=I R=UR
UL=I*ZL=jXLI=jUL
UC=I*ZC=-jXCI=-jUC
U=UR+UL+UC=UR+ j(UL-UC)
S=U I*=P+jQ
Z=R+ j(XL-XC)

33.

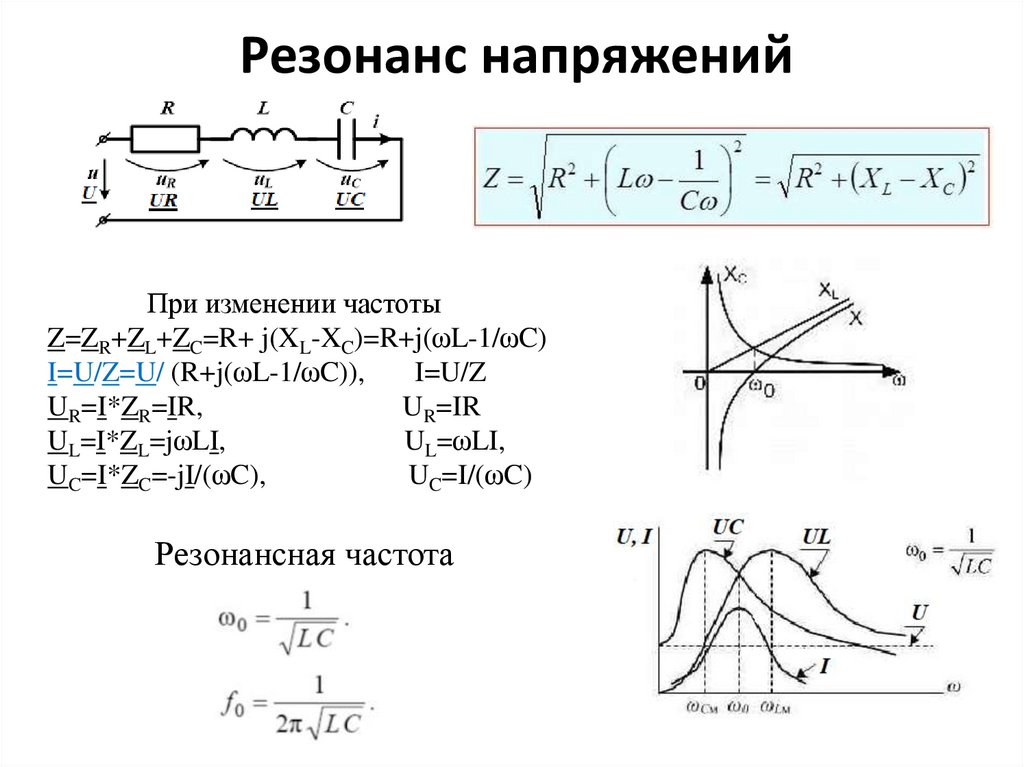
Резонанс напряжений
При XL=XC напряжения UL=UC
Сопротивление минимально Z=R,
а ток максимален I=U/R
Входное напряжение U=UR
U=UR+UL+UC=UR+ j(UL-UC)=UR
Напряжение на L, C может быть больше U
UL/U=UC/U =ωL/R=1/(ωCR)
Если ток I=I
UR=I*ZR=I R=UR
UL=I*ZL=jXLI=jUL
UC=I*ZC=-jXCI=-jUC
S=U I*=P+jQ=P,
нет реактивной мощности Q=0, cosφ =1

34.

Резонанс напряжений
При изменении частоты
Z=ZR+ZL+ZC=R+ j(XL-XC)=R+j(ωL-1/ωC)
I=U/Z=U/ (R+j(ωL-1/ωC)),
I=U/Z
UR=I*ZR=IR,
UR=IR
UL=I*ZL=jωLI,
UL=ωLI,
UC=I*ZC=-jI/(ωC),
UC=I/(ωC)
Резонансная частота

35.

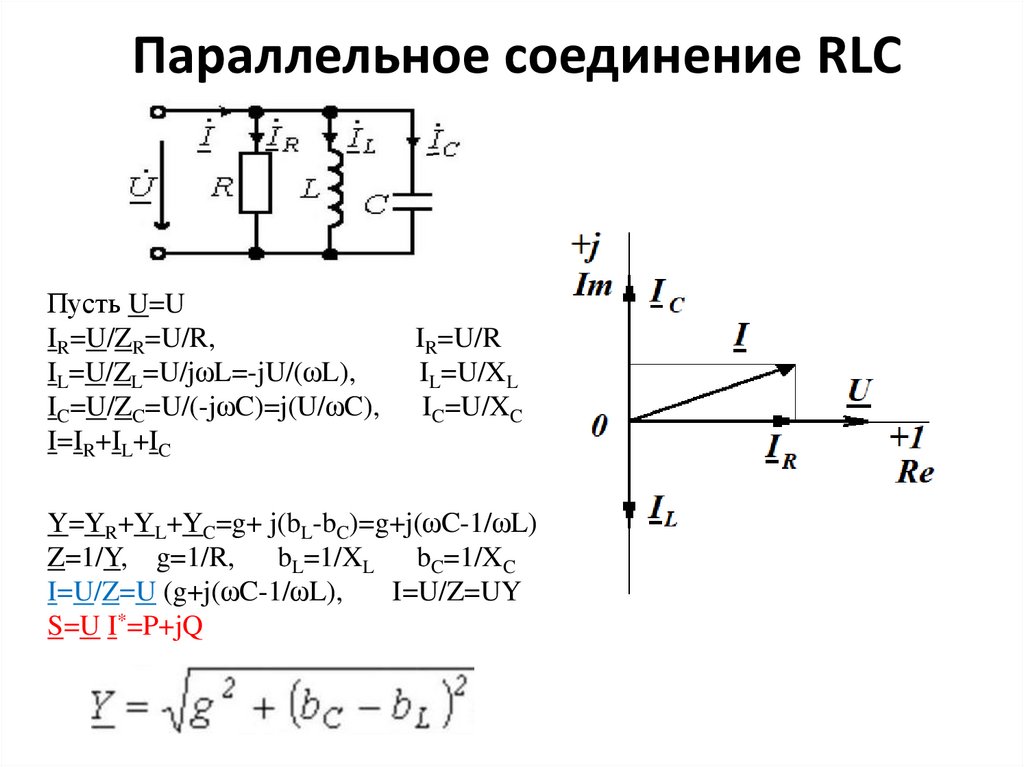
Параллельное соединение RLC
Дано: Напряжение U, все сопротивления R, XC, XL
Найти: Все разные напряжения и токи
Напряжение только одно - U. Токи - I, IR, IL, IC
В комплексной форме записываем все величины.
Если начальная фаза напряжения Ψ=0, то U=U
Резистор ZR=R, конденсатор ZC=-jXC, катушка индуктивности ZL=+jXL
IR=U/ZR=U/R,
IR=U/R
IL=U/ZL=U/jXL,
IL=U/XL
IC=U/ZC=U/(-jXC),
IC=U/XC
I=IR+IL+IC
Y=YR+YL+YC=g+ j(bC-bL)=g+j(ωC-1/ωL)
Z=1/Y, g=1/R, bL=1/XL bC=1/XC
I=U/Z=U (g+j(ωC-1/ωL),
I=U/Z=UY

36.

Параллельное соединение RLC
Пусть U=U
IR=U/ZR=U/R,
IL=U/ZL=U/jωL=-jU/(ωL),
IC=U/ZC=U/(-jωC)=j(U/ωC),
I=IR+IL+IC
IR=U/R
IL=U/XL
IC=U/XC
Y=YR+YL+YC=g+ j(bL-bC)=g+j(ωC-1/ωL)
Z=1/Y, g=1/R, bL=1/XL bC=1/XC
I=U/Z=U (g+j(ωC-1/ωL),
I=U/Z=UY
S=U I*=P+jQ

37.

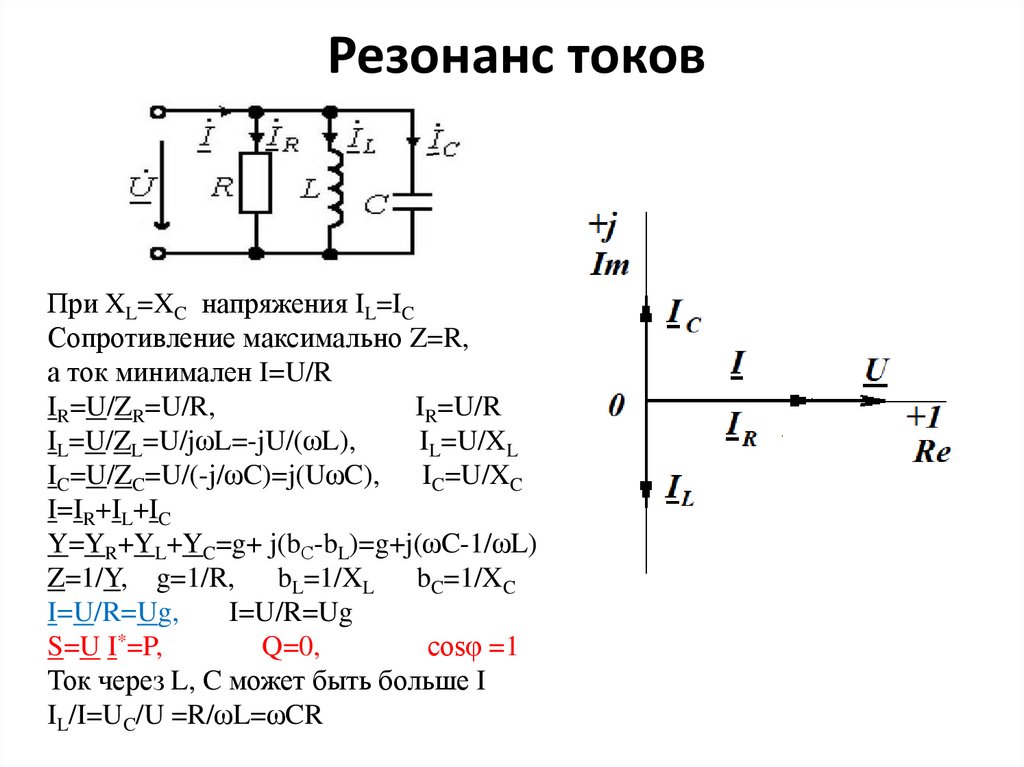
Резонанс токов
При XL=XC напряжения IL=IC
Сопротивление максимально Z=R,
а ток минимален I=U/R
IR=U/ZR=U/R,
IR=U/R
IL=U/ZL=U/jωL=-jU/(ωL),
IL=U/XL
IC=U/ZC=U/(-j/ωC)=j(UωC), IC=U/XC
I=IR+IL+IC
Y=YR+YL+YC=g+ j(bС-bL)=g+j(ωC-1/ωL)
Z=1/Y, g=1/R, bL=1/XL bC=1/XC
I=U/R=Ug,
I=U/R=Ug
S=U I*=P,
Q=0,
cosφ =1
Ток через L, C может быть больше I
IL/I=UC/U =R/ωL=ωCR

38.

Настройка на резонанс
При изменении частоты
Y=YR+YL+YC=g+ j(bC-bL)=g+j(ωC-1/ωL)
Z=1/Y, g=1/R, bL=1/XL bC=1/XC
I=U/Z=U (g+j(ωC-1/ωL),
I=U/Z=UY
IR=U/ZR=UR,
IR=U/R
IL=U/ZL=U/jωL,
IL=U/ωL,
IC=U/ZC=U/(-j/ωC),
IC=U*(ωC)
I=IR+IL+IC
Резонансная частота