Similar presentations:
Анализ установившегося синусоидального режима в простейших линейных цепях
1. Дисциплина: Основы теории цепей
2. Лекция №4
Тема: Анализустановившегося
синусоидального режима
в простейших линейных
цепях
3. Учебные вопросы
1. Режимы работы последовательнойRLC-цепи.
2. Расчетные соотношения в
последовательной RLC-цепи.
Треугольники напряжений и
сопротивлений.
3. Режимы работы параллельной RLCцепи.
4. Расчетные соотношения в
параллельной RLC-цепи. Треугольники
токов и проводимостей.
4. Литература
1. Попов В.П. Основытеории цепей: Учебник
для вузов спец.
"Радиотехника".-М.:
Высшая школа, 2007, с.
122-137.
5.
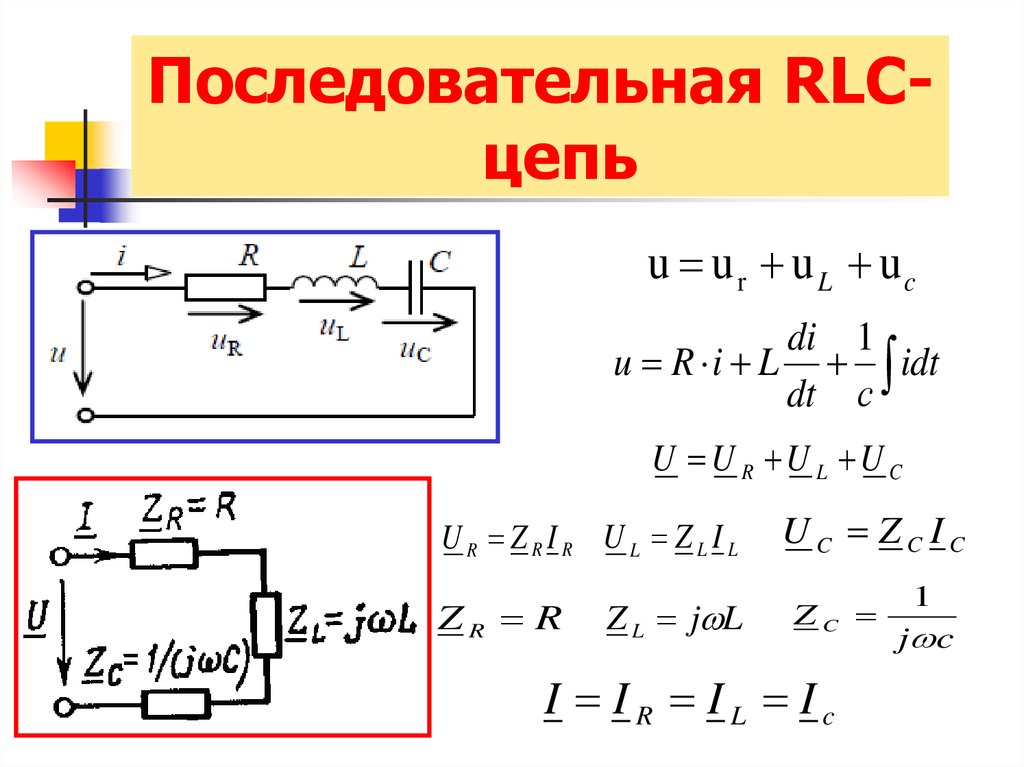
Последовательная RLCцепьu u r u L uc
di 1
u R i L idt
dt с
U U R U L U C
UR ZRIR UL ZLIL
ZR R
Z L j L
UC ZC IC
ZC
I IR IL Ic
1
j c
6.
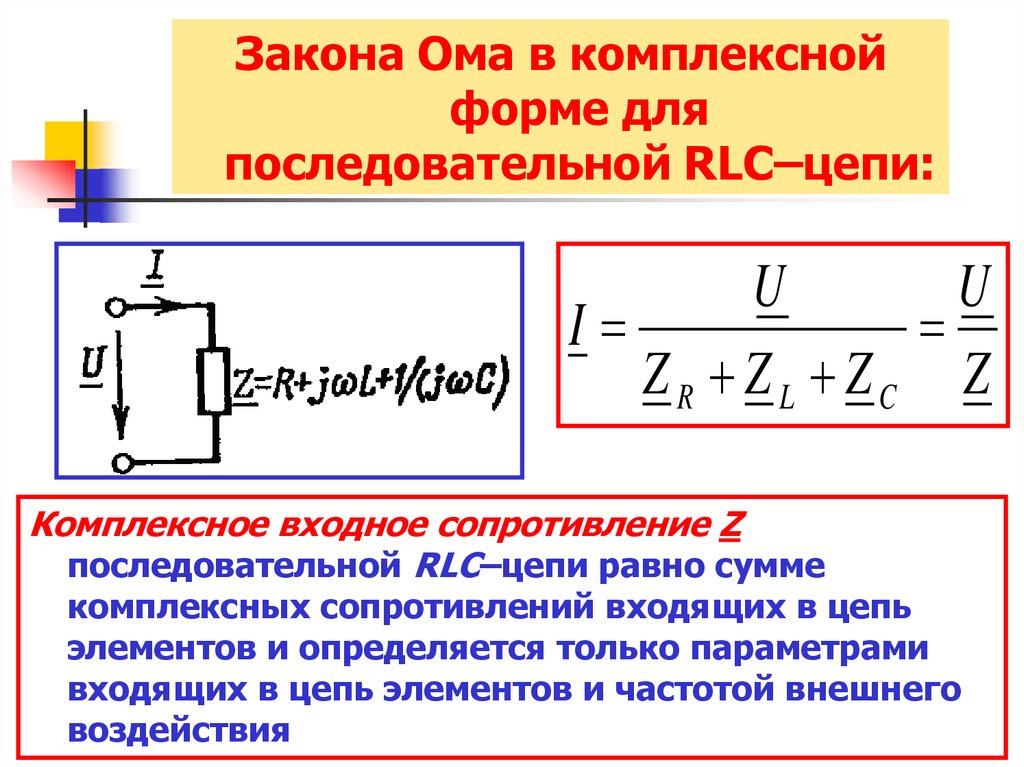
Закона Ома в комплекснойформе для
последовательной RLC–цепи:
U
U
I
ZR ZL ZC Z
Комплексное входное сопротивление Z
последовательной RLC–цепи равно сумме
комплексных сопротивлений входящих в цепь
элементов и определяется только параметрами
входящих в цепь элементов и частотой внешнего
воздействия
7. Комплексное входное сопротивление
1Z Z R Z L Z C R j ( L ) R j ( x L xC )
c
j
R jx Z cos jZ sin Ze
Модуль и аргумент комплексного входного
сопротивления:
1 2
Z R ( L )
c
2
L 1 /( c)
arctg
R
8. Вещественная и мнимая части комплексного сопротивления
Активное R и реактивное xсопротивления:
R Re Z Re( Z cos jZ sin ) Z cos
x JmZ Jm(Z cos jZ sin ) Z sin
9. Режимы работы последовательной RLC-цепи
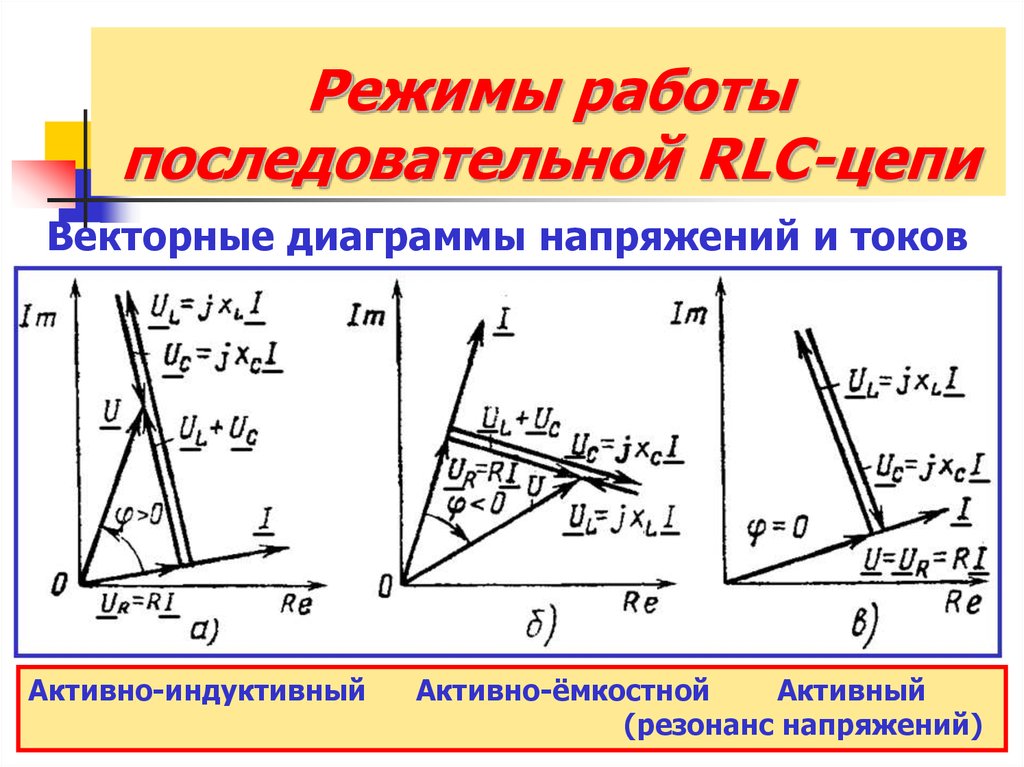
Векторные диаграммы напряжений и токовАктивно-индуктивный
Активно-ёмкостной
Активный
(резонанс напряжений)
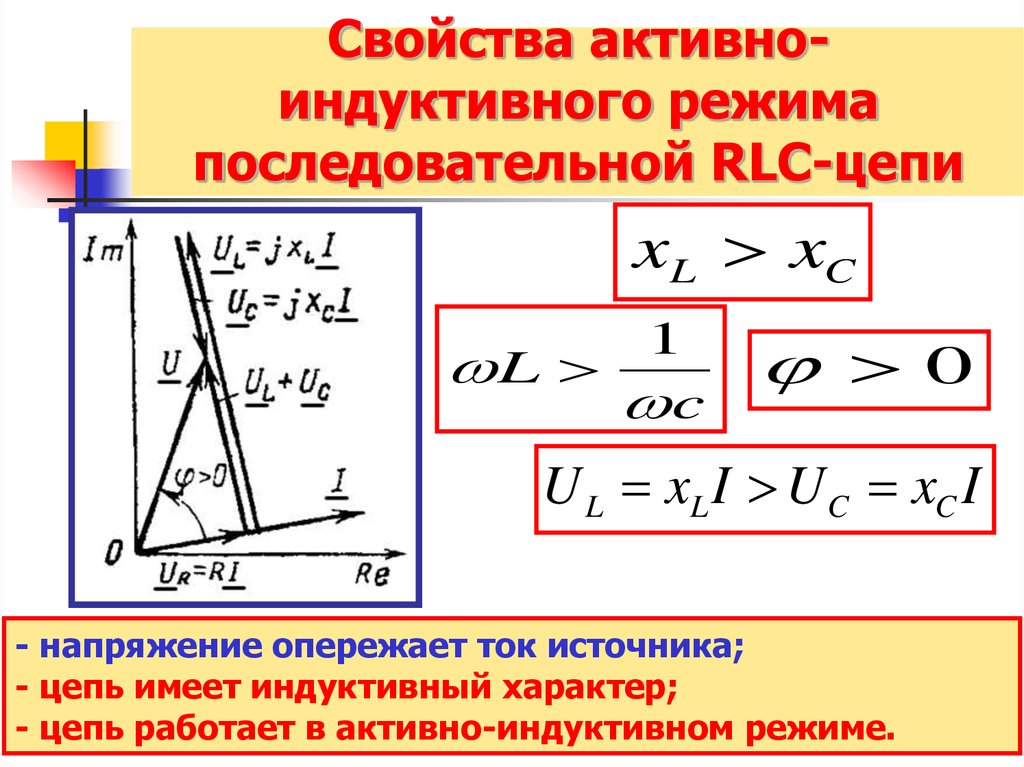
10. Свойства активно-индуктивного режима последовательной RLC-цепи
Свойства активноиндуктивного режимапоследовательной RLC-цепи
xL xC
1
L
c
0
U L xL I U C xC I
- напряжение опережает ток источника;
- цепь имеет индуктивный характер;
- цепь работает в активно-индуктивном режиме.
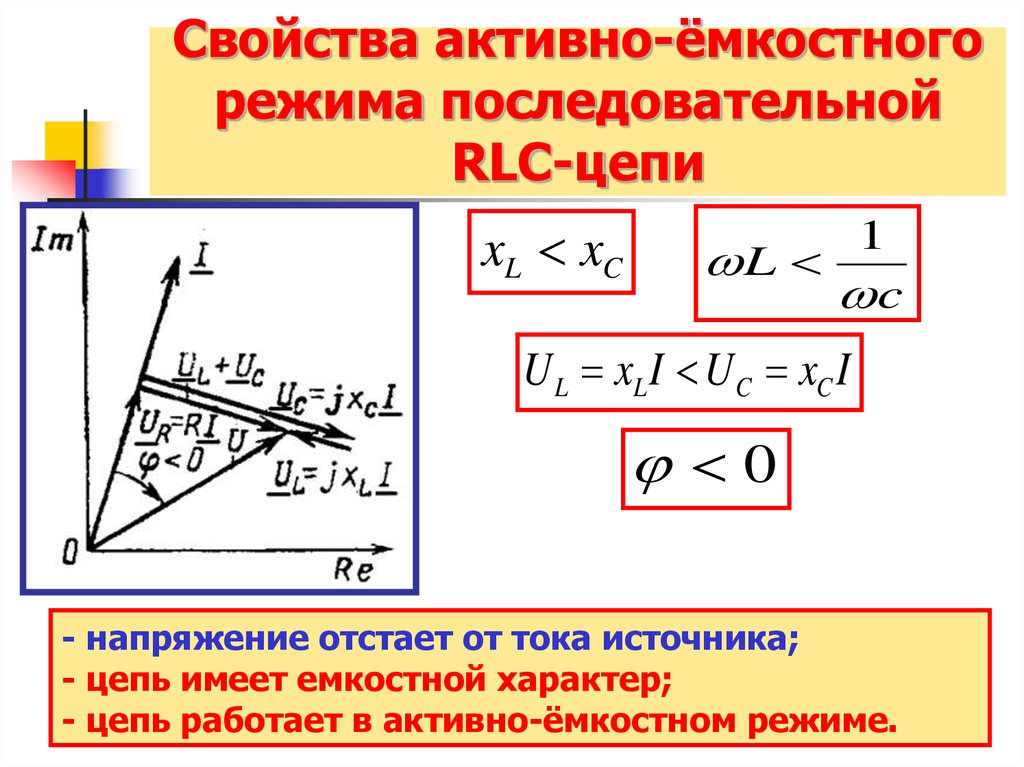
11. Свойства активно-ёмкостного режима последовательной RLC-цепи
xL xC1
L
c
U L xL I U C xC I
0
- напряжение отстает от тока источника;
- цепь имеет емкостной характер;
- цепь работает в активно-ёмкостном режиме.
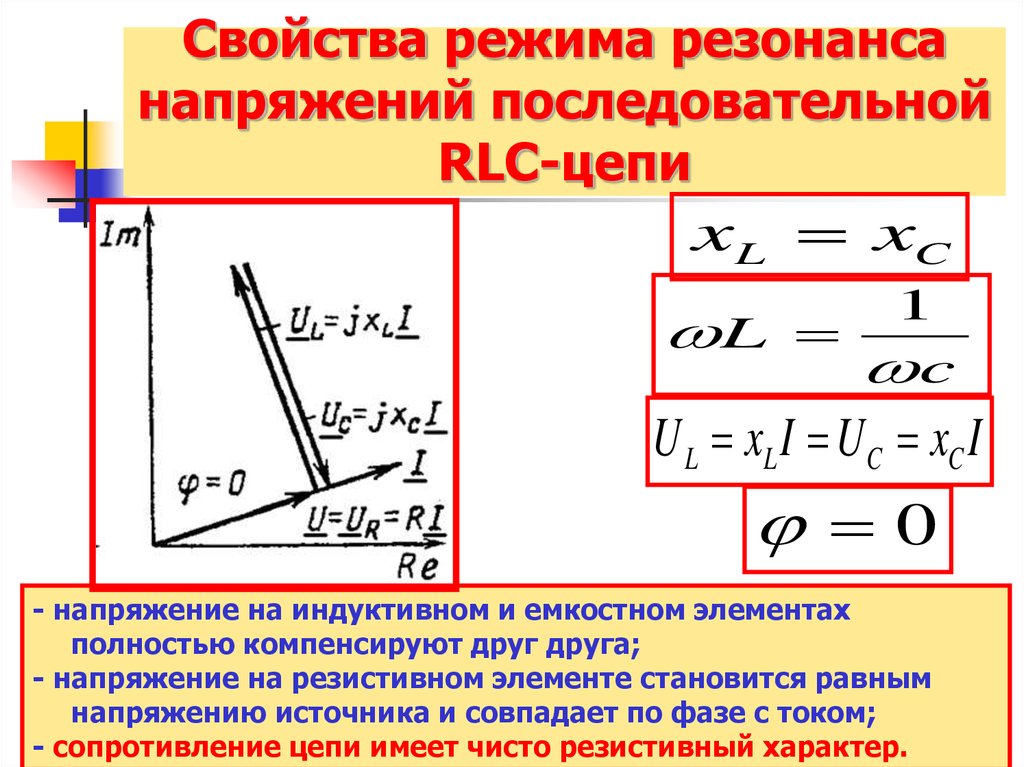
12. Свойства режима резонанса напряжений последовательной RLC-цепи
xL xC1
L
c
U L xL I U C xC I
0
- напряжение на индуктивном и емкостном элементах
полностью компенсируют друг друга;
- напряжение на резистивном элементе становится равным
напряжению источника и совпадает по фазе с током;
- сопротивление цепи имеет чисто резистивный характер.
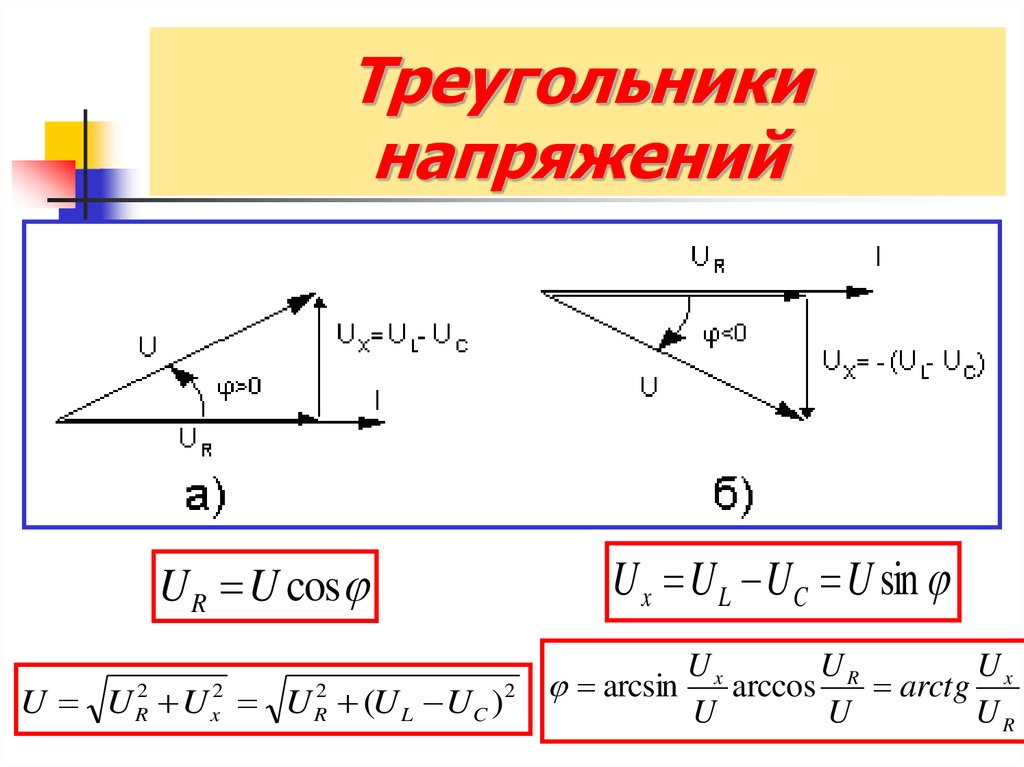
13. Треугольники напряжений
U R U cosU x U L UC U sin
U U R2 U x2 U R2 (U L UC )2
Ux
UR
Ux
arcsin
arccos
arctg
U
U
UR
14. Треугольник сопротивлений и закон Ома
R Z cosZ R 2 x 2 R 2 ( xL xC )2 R 2 ( L
1 2
)
c
x xL xc Z sin
U
xL xC
R
xL xC
I
arcsin
arccos arctg
Z
Z
Z
R
Im
Um
Z
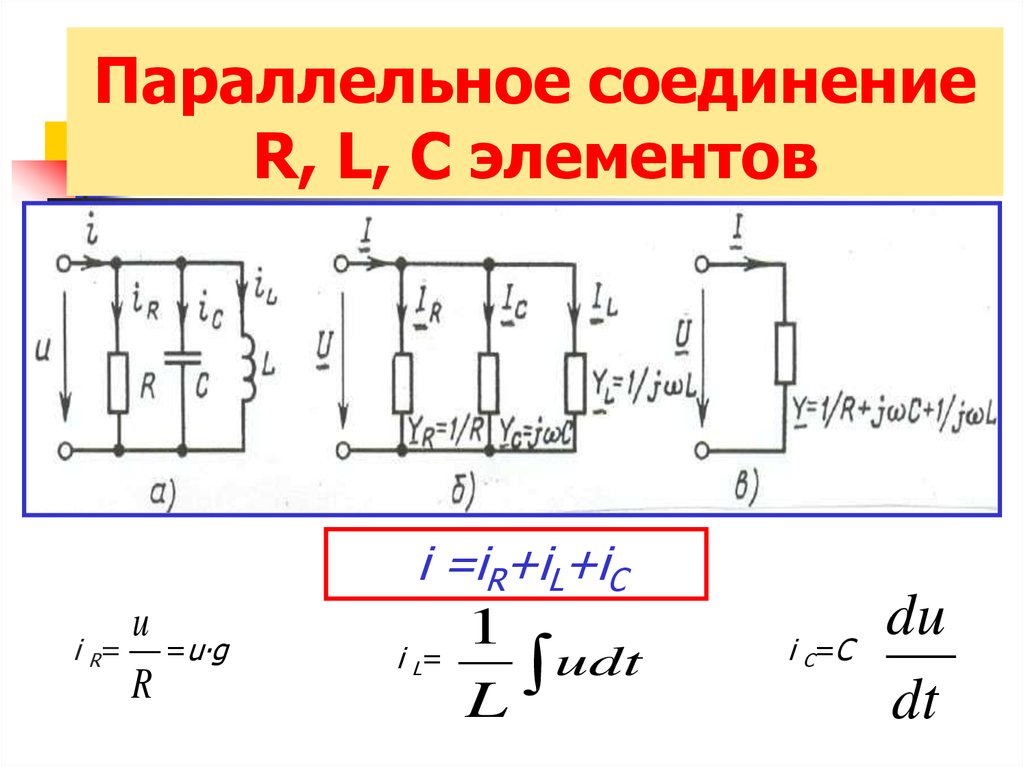
15. Параллельное соединение R, L, C элементов
i =iR+iL+iCu
i R=
R
=u∙g
i L=
1
udt
L
i C=C
du
dt
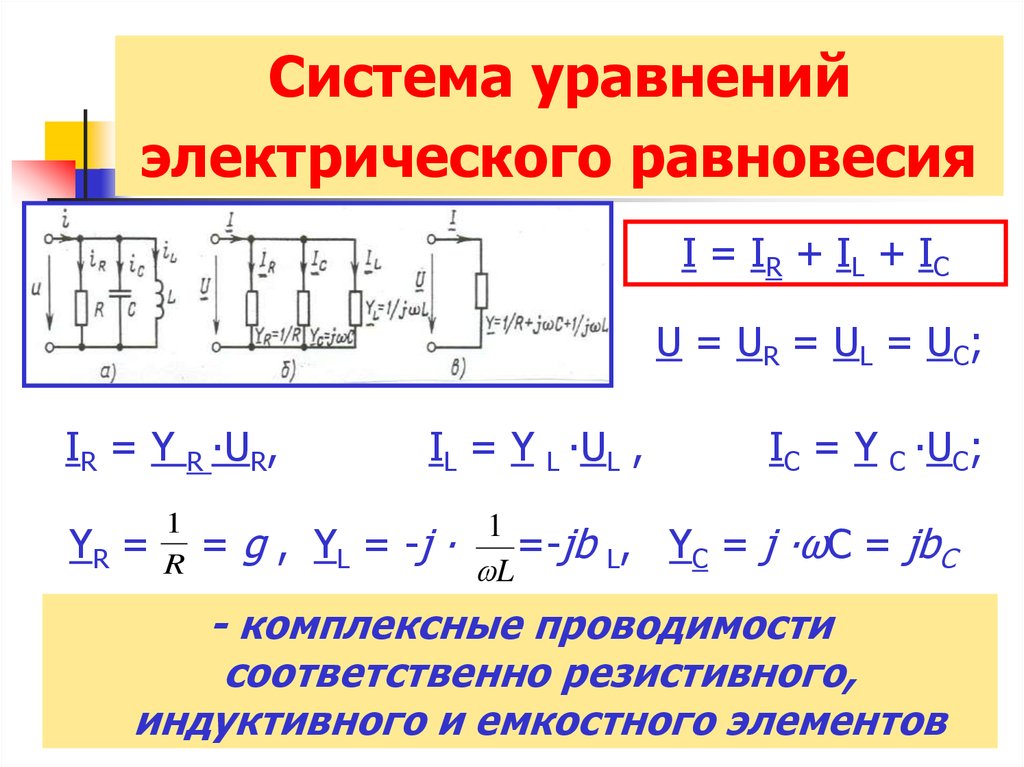
16. Система уравнений электрического равновесия
I = IR + IL + ICU = UR = UL = UC ;
IR = Y R ∙UR,
YR =
1
R
IL = Y L ∙UL ,
= g , YL = -j ∙
1
=-jb L,
L
IC = Y C ∙UC;
YC = j ∙ωC = jbC
- комплексные проводимости
соответственно резистивного,
индуктивного и емкостного элементов
17. Закон Ома в комплексной форме для параллельной RLC-цепи:
Закон Ома в комплекснойформе для параллельной RLCцепи:
I = (YR + YL + YC) U = YU
где Y = YR + YL + YC - комплексная проводимость RLCцепи, равная сумме комплексных проводимостей
входящих в цепь идеализированных элементов
Комплексная проводимость параллельной RLC-цепи
не зависит от амплитуды (действующего
значения) и начальной фазы внешнего
воздействия, а определяется только параметрами
входящих в цепь элементов и частотой внешнего
воздействия
18. Комплексная проводимость параллельной RLC-цепи
Y = YR + YL + YC = g + j ∙(bC-bL) =1
1
j( C )
R
L
j
Y = y ∙e
y=
g (bC bL )
2
2
2
= 1 C 1
L
R
ν = arctg
bC bL
g
2
1
C
L
= arctg
1
R
Вывод: характер проводимости, а, следовательно, и
характер сопротивления цепи зависит от соотношения
индуктивной и емкостной проводимостей.
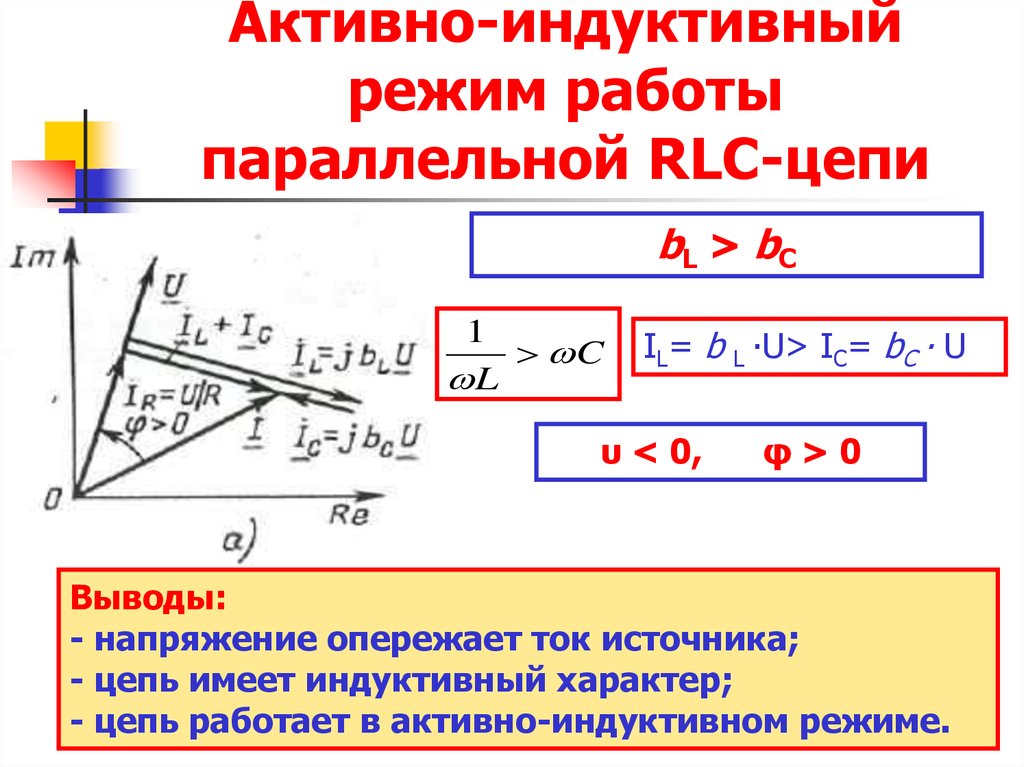
19. Активно-индуктивный режим работы параллельной RLC-цепи
bL > bC1
C
L
IL= b L ∙U> IC= bC ∙ U
υ < 0,
φ>0
Выводы:
- напряжение опережает ток источника;
- цепь имеет индуктивный характер;
- цепь работает в активно-индуктивном режиме.
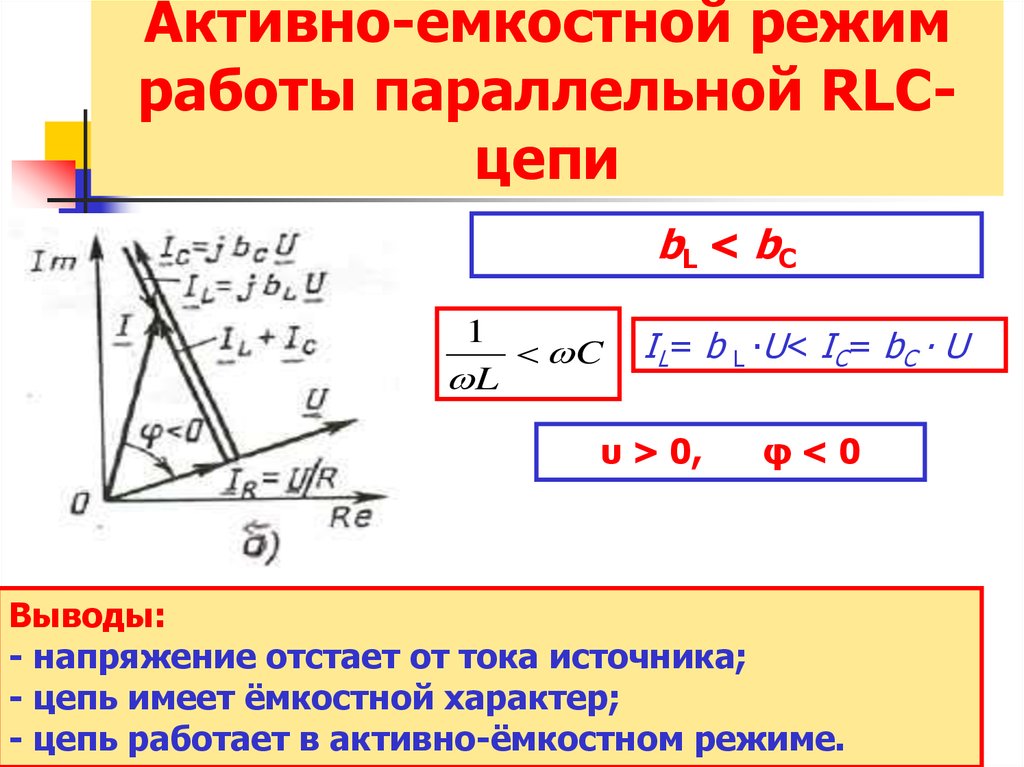
20. Активно-емкостной режим работы параллельной RLC-цепи
Активно-емкостной режимработы параллельной RLCцепи
bL < bC
1
C
L
IL= b L ∙U< IC= bC ∙ U
υ > 0,
φ<0
Выводы:
- напряжение отстает от тока источника;
- цепь имеет ёмкостной характер;
- цепь работает в активно-ёмкостном режиме.
21. Активный (резонанс токов) режим работы параллельной RLC-цепи
bL = bC1
C
L
IL= b L ∙U= IC= bC ∙ U
υ = 0,
φ=0
Выводы:- индуктивный и емкостной токи полностью
компенсируют друг друга, в результате чего ток через
резистивный элемент равен току источника и совпадает
по фазе с напряжением;
- проводимость цепи имеет чисто резистивный характер;
- цепь работает в режиме резонанса токов.
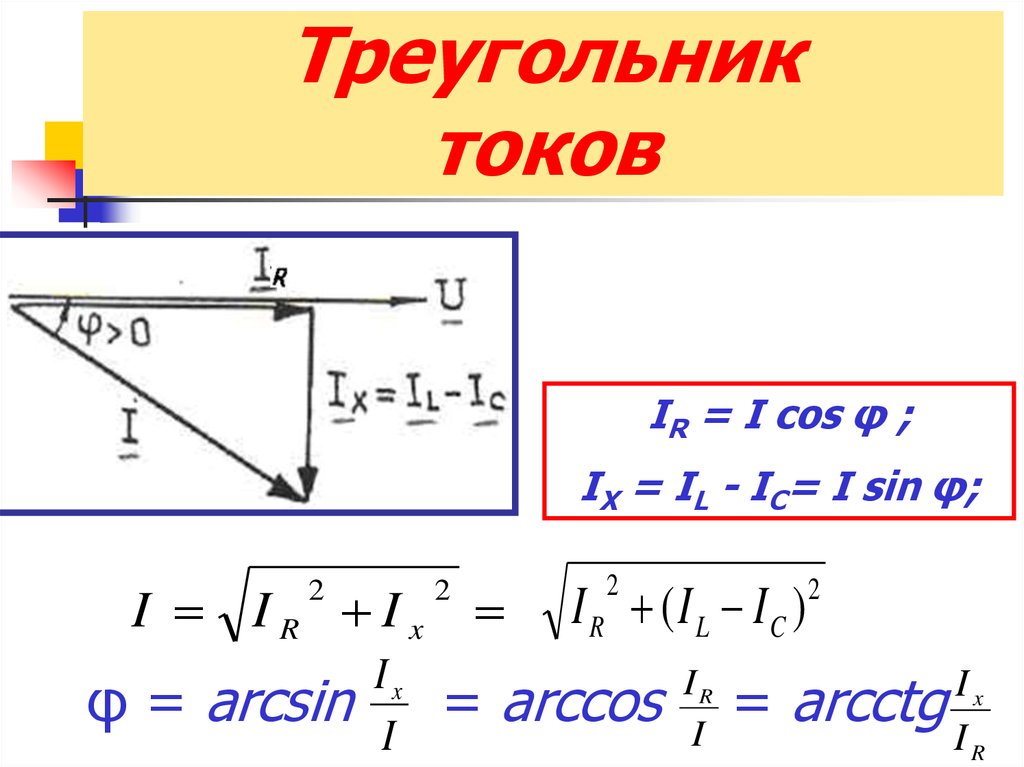
22. Треугольник токов
IR = I cos φ ;IX = IL - IC= I sin φ;
I IR Ix
2
φ = arcsin
Ix
I
2
I R ( I L IC )
2
= arcсos
IR
I
=
2
Ix
arсctg I
R
23. Треугольник проводимостей
g =y cos φ; b =bL - bC= y sin φ ;y g b
2
2
g (bL bC )
2
b
φ = arcsin
=
y
g
b
=arcсos
= arcсtg
y
g
2
.











 electronics
electronics








