Similar presentations:
Законы в комплексной форме, мощность и векторные диаграммы. Лекция 6
1.
ТОЭ Часть №1. Лк. №6.Тема: законы в комплексной форме,
мощность и векторные диаграммы
2.
ЗАКОН ОМАВ КОМПЛЕКСНОЙ
ФОРМЕ
3.
Закон Ома в комплексной формеоснован на символическом методе
и справедлив для линейных цепей
с гармоническими напряжениями
и токами
Этот закон следует из
физической взаимосвязи
между током и напряжением
отдельных элементов цепи
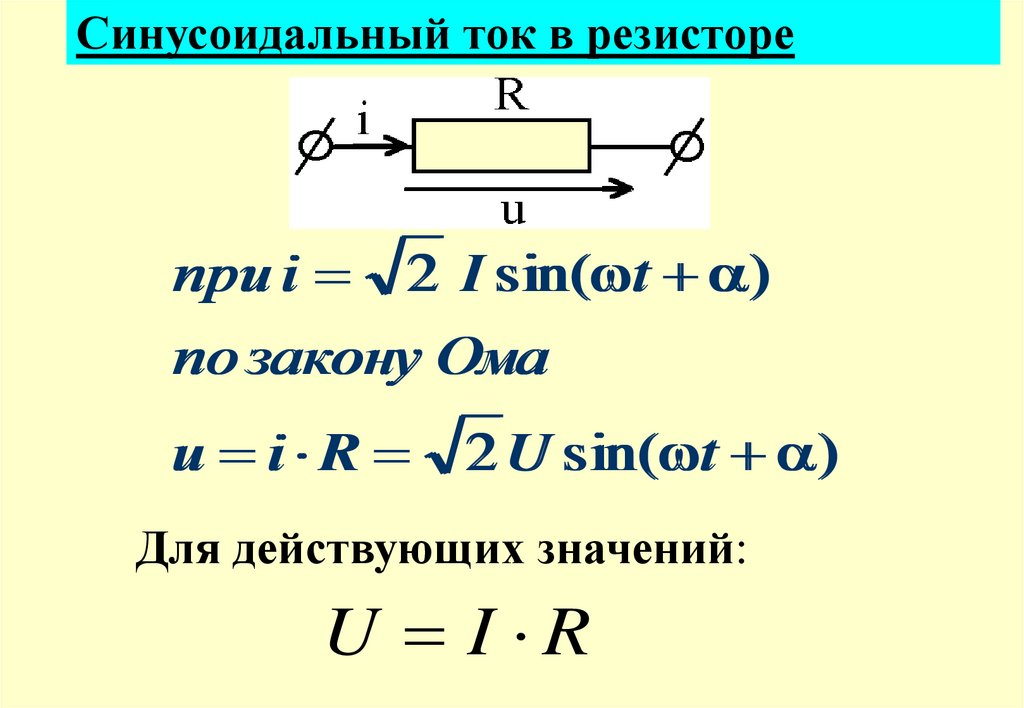
4.
Синусоидальный ток в резисторепри i 2 I sin( t )
по закону Ома
u i R 2 U sin( t )
Для действующих значений:
U I R
5.
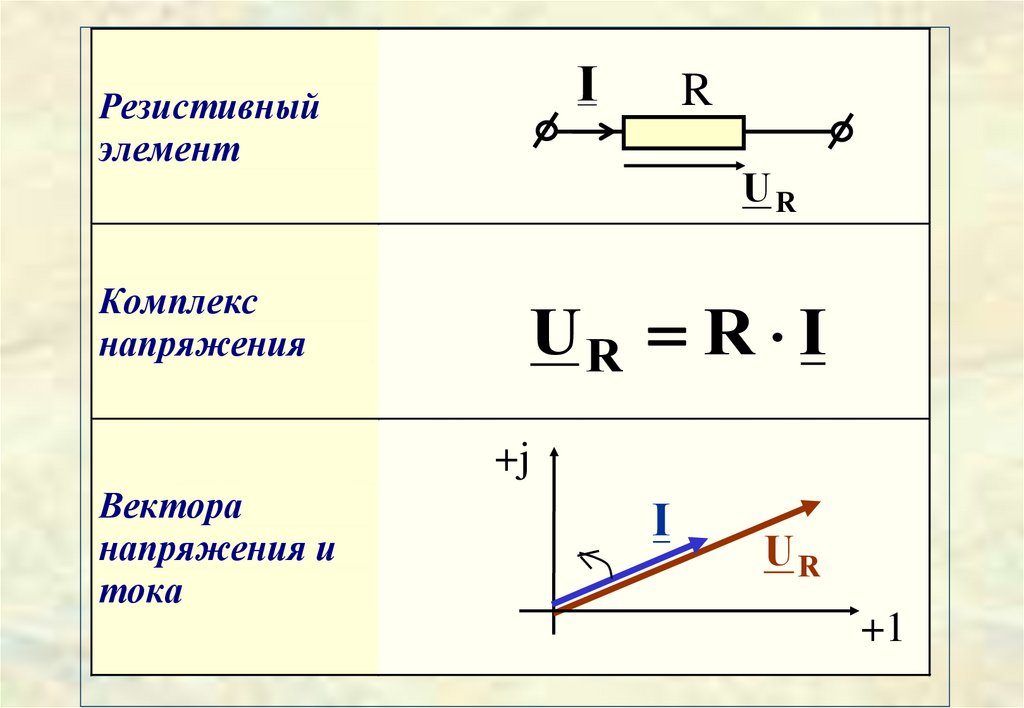
IРезистивный
элемент
Комплекс
напряжения
R
UR
UR R I
+j
Вектора
напряжения и
тока
I
UR
+1
6.
На комплексной плоскостивектор напряжения
резистивного элемента
совпадает по направлению
с вектором своего тока
7. Мгновенная активная мощность:
22
p u i 2 I R sin t
I R
1 cos 2 t
2
Средняя активная мощность за период Т
T
1
2
P p t dt I R, Bт
T0
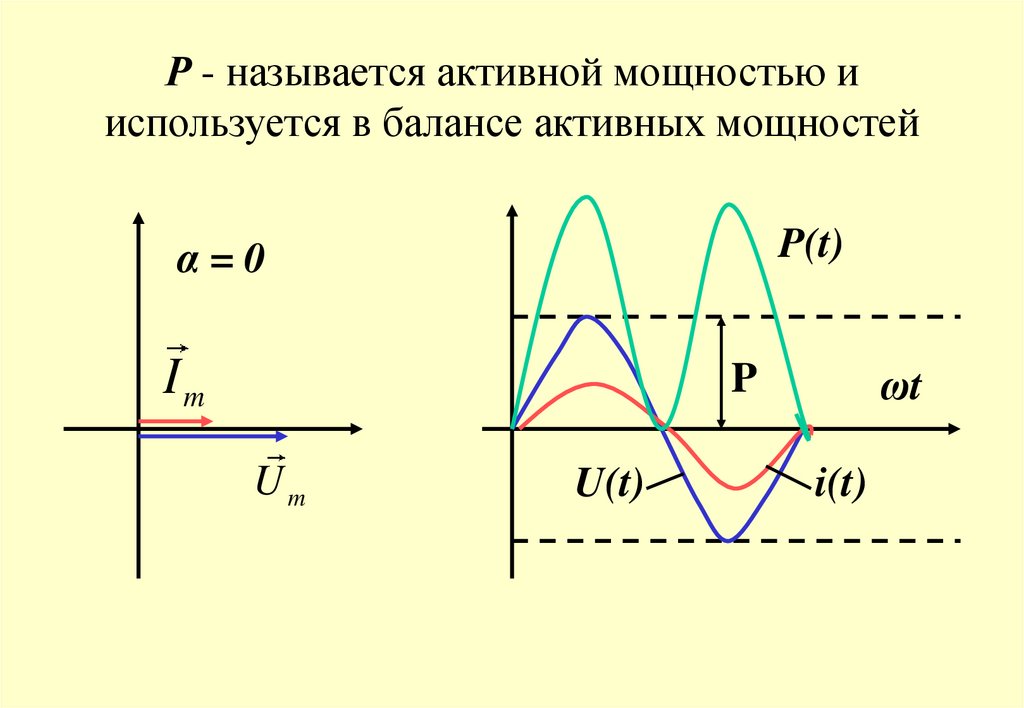
8. Р - называется активной мощностью и используется в балансе активных мощностей
P(t)α=0
Im
ωt
P
Um
U(t)
i(t)
9.
Синусоидальный ток в индуктивностипри i 2 I sin( t )
по закону электромагнитной
индукции :
di
u L
2 I L cos( t )
dt
0
2 U sin( t 90 )
10.
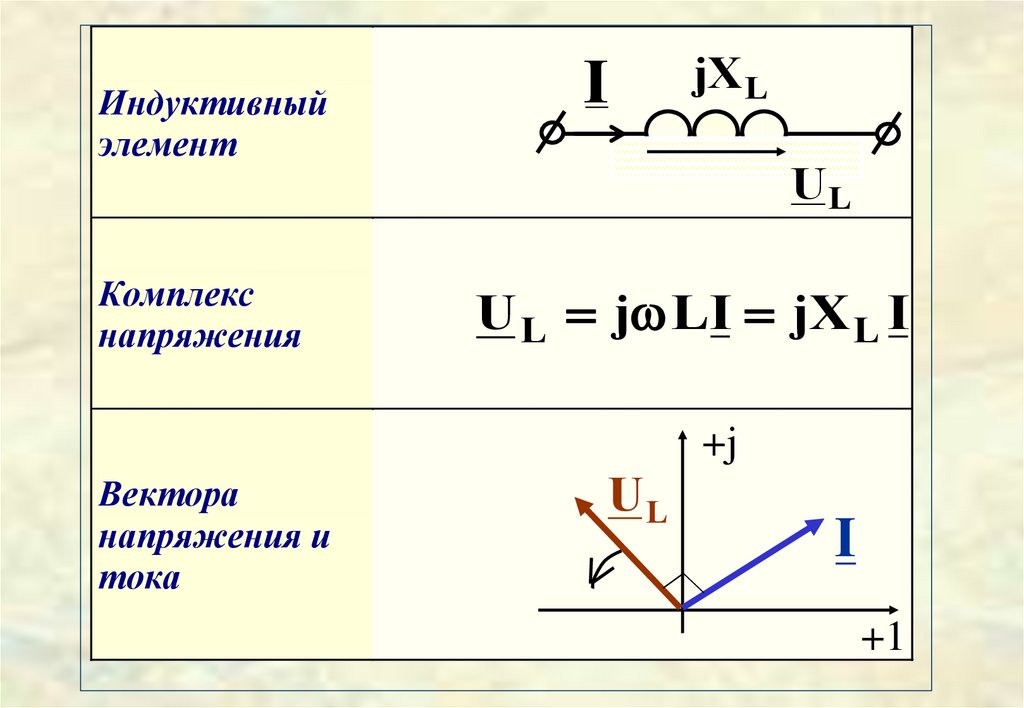
Индуктивныйэлемент
Комплекс
напряжения
I
jXL
UL
U L j LI jX L I
+j
Вектора
напряжения и
тока
UL
I
+1
11.
На комплексной плоскостивектор напряжения
индуктивного элемента
опережает по направлению
вектор своего тока
на 90 градусов
12.
Для действующих значений:где X
U I L I X L
- индуктивное реактивное
L
L
сопротивление
В индуктивности напряжение опережает ток
0
на 90
Мгновенная активная мощность равна:
р u i
2 I X L sin( t ) cos( t )
2
QL sin 2( t )
13.
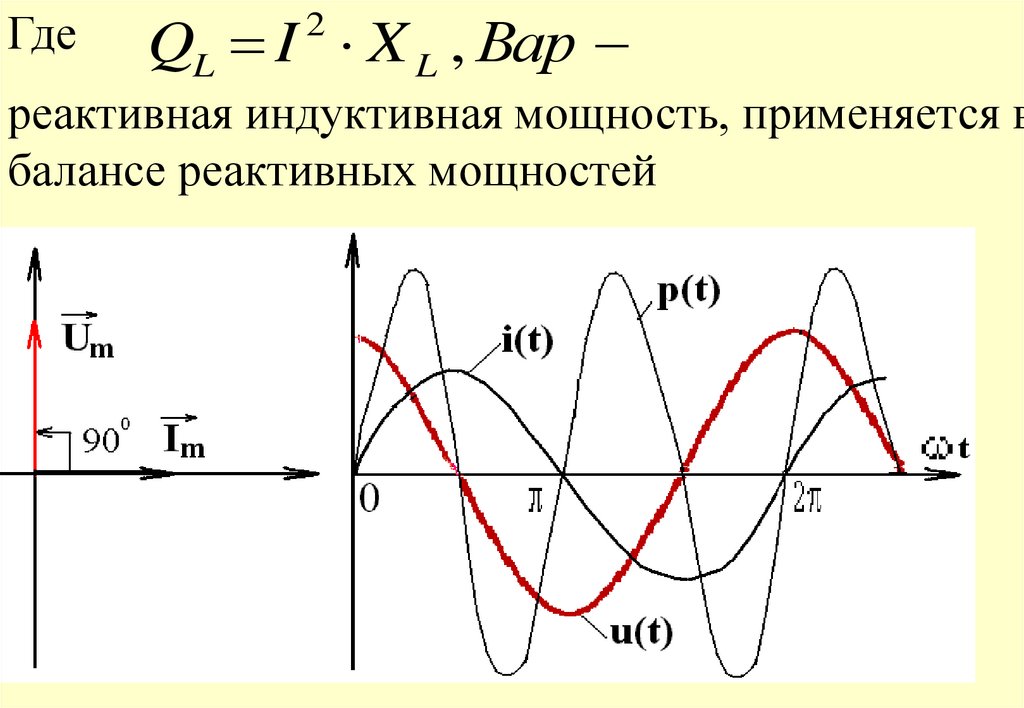
ГдеQL I X L , Вар
2
реактивная индуктивная мощность, применяется в
балансе реактивных мощностей
14.
Когдаp 0 индуктивность потребляет
энергию, которая запасается в магнитном
поле;
Когда p 0 запасенная энергия
возвращается в сеть.
Средняя за период Т активная мощность Р=0.
15.
Синусоидальный ток в ёмкостиi
С
i 2 I sin( t )
напряжения получим :
1
I
u i (t ) dt 2
cos( t )
С
C
0
2 U sin( t 90 )
при
для
16.
Для действующих значений:I
U
I XC
C
1
где X С
С
реактивное емкостное
сопротивление
17.
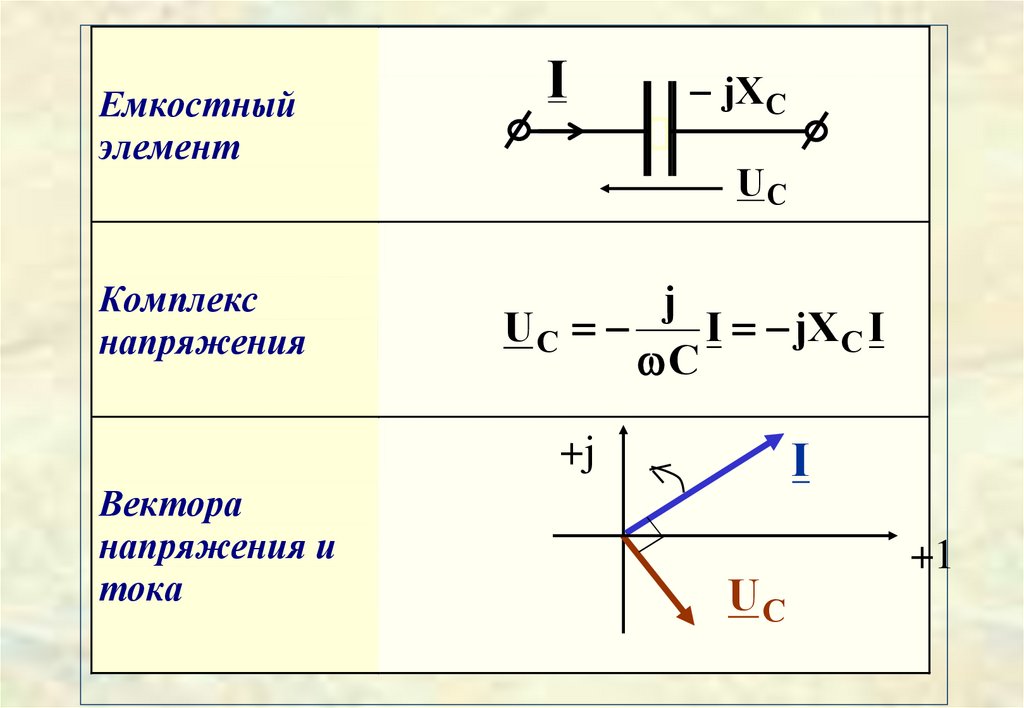
Емкостныйэлемент
Комплекс
напряжения
I
jXC
UC
j
UC
I jX C I
C
I
+j
Вектора
напряжения и
тока
UC
+1
18.
На комплексной плоскостивектор напряжения
емкостного элемента
отстает по направлению
от вектора своего тока
на 90 градусов
19.
В ёмкости напряжение отстаёт от токана 90
0
Мгновенная активная мощность равна:
р u i
2 I X C sin( t ) cos( t )
2
QC sin 2( t )
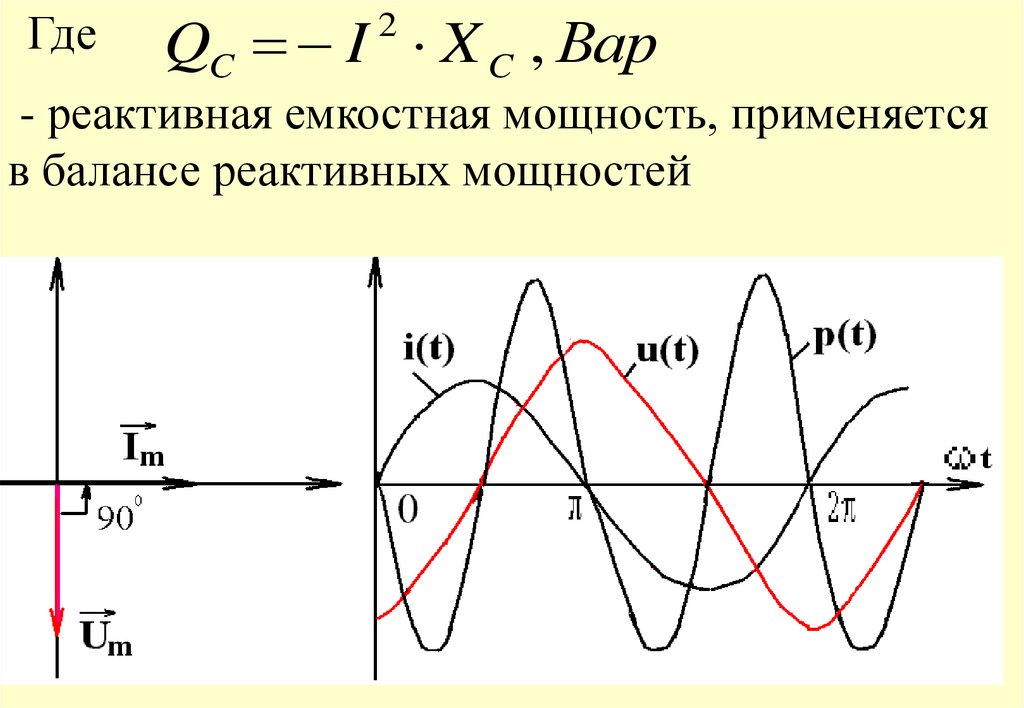
20.
ГдеQC I X C , Вар
2
- реактивная емкостная мощность, применяется
в балансе реактивных мощностей
Средняя за период Т активная мощность Р=0.
21.
Когдаp 0 ёмкость потребляет
энергию, которая запасается в электрическом
поле;
Когда p 0 запасенная энергия
возвращается в сеть.
Средняя за период Т активная мощность Р=0.
22.
Где:X L L
XC 1
- индуктивное
сопротивление (Ом)
- емкостное
C
сопротивление (Ом)
23.
Закон Ома в комплексной формедля отдельных элементов аналогичен
закону Ома для резистивного элемента
на постоянном токе.
Для символического метода
необходимо составить комплексную
схему замещения с комплексными
сопротивлениями и с комплексами
действующих значений токов и
напряжений
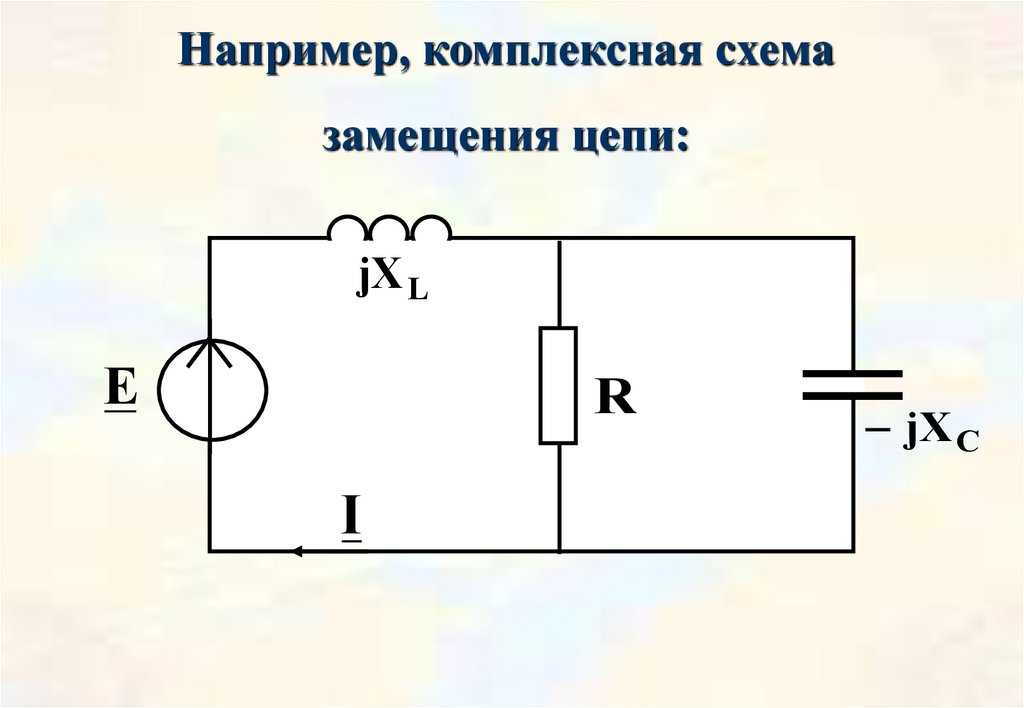
24.
Например, комплексная схемазамещения цепи:
jX L
E
R
I
jX C
25.
R( jX C )Z jX L
R jX C
E
I
Z
26.
Где:j
Z RЭ jX Э Z e
– эквивалентное комплексное
сопротивление цепи (Ом)
2
2
Z RЭ X Э
- модуль сопротивления (Ом)
XЭ
arctg
RЭ
-аргумент (фаза)
сопротивления (Град)
27.
ЗАКОНЫ КИРХГОФАВ КОМПЛЕКСНОЙ
ФОРМЕ
28.
Сложению и вычитаниюгармонических токов и напряжений
с одинаковой угловой частотой
в законах Кирхгофа
соответствует сложение и вычитание
их комплексных величин
29.
1. ПЕРВЫЙЗАКОН КИРХГОФА
В КОМПЛЕКСНОЙ
ФОРМЕ
30.
Для любого узла комплексной схемызамещения цепи алгебраическая
сумма комплексных значений токов
равна нулю
31.
I0
k
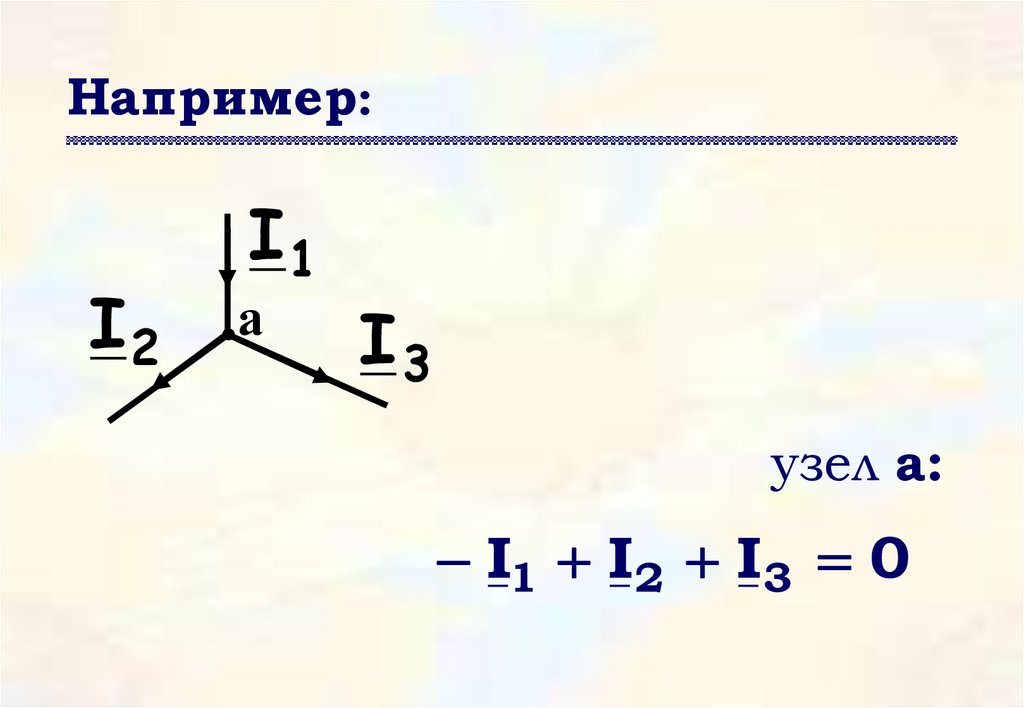
32.
Например:I2
I1
а
I3
узел а:
I1 I2 I3 0
33.
2. ВТОРОЙЗАКОН КИРХГОФА
В КОМПЛЕКСНОЙ
ФОРМЕ
34.
Для любого контура комплексной схемызамещения цепи алгебраическая
сумма комплексов напряжений
на пассивных элементах равна
алгебраической сумме комплексов
ЭДС и напряжений на
источниках тока
35.
U n E k UJq U p36.
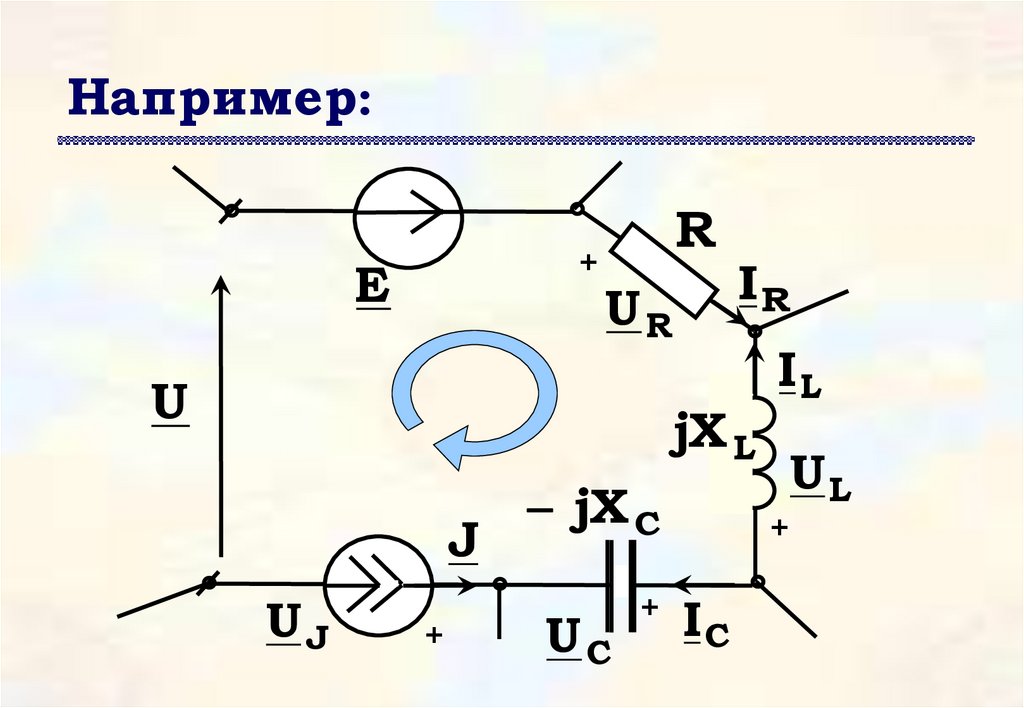
Например:+
E
R
UR
U
IR
jX L
J
UJ
+
jX C
UC
+
IL
+
IC
UL
37.
UR UL UC E U J Uили
RIR jX L I L ( jX C)I C E U J U
38.
3. МЕТОД ЗАКОНОВКИРХГОФА
В КОМПЛЕКСНОЙ
ФОРМЕ
39.
Решая комплексные алгебраическиеуравнения, составленные
по законам Кирхгофа в
комплексной форме, можно
определить комплексы токов и
напряжений в комплексной
схеме замещения цепи
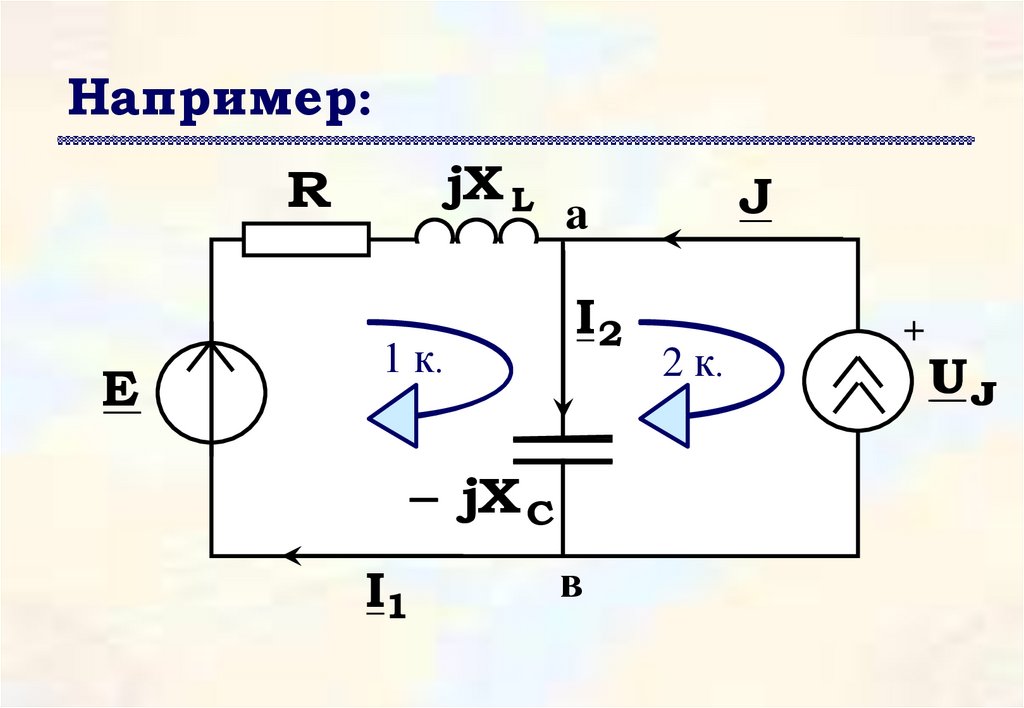
40.
Например:jX L
R
E
1 к.
I2
jX C
I1
J
a
в
2 к.
+
UJ
41.
ny 2nв 3
n1 n y 1 1
n 2 n в n1 2
42.
a:I1 I2 J 0
1к :
(R jX L ) I1 ( jX C ) I2 E
2к :
( jX C ) I2 U J
43.
11
(R jX L ) ( jX C )
0
jX C
0
I1
0
I2
1
UJ
J
E
0
44.
ЗАКОНЫ ОМА И КИРХГОФАВ КОМПЛЕКСНОЙ ФОРМЕ
ИМЕЮТ ТАКОЙ ЖЕ ВИД КАК
И ДЛЯ ЦЕПЕЙ С ПОСТОЯННЫМИ
ТОКАМИ, ПОЭТОМУ К
КОМПЛЕКСНЫМ СХЕМАМ
ПРИМЕНИМЫ ВСЕ ИЗВЕСТНЫЕ
МЕТОДЫ РАСЧЕТА,
НО В КОМПЛЕКСНОЙ ФОРМЕ
45.
46.
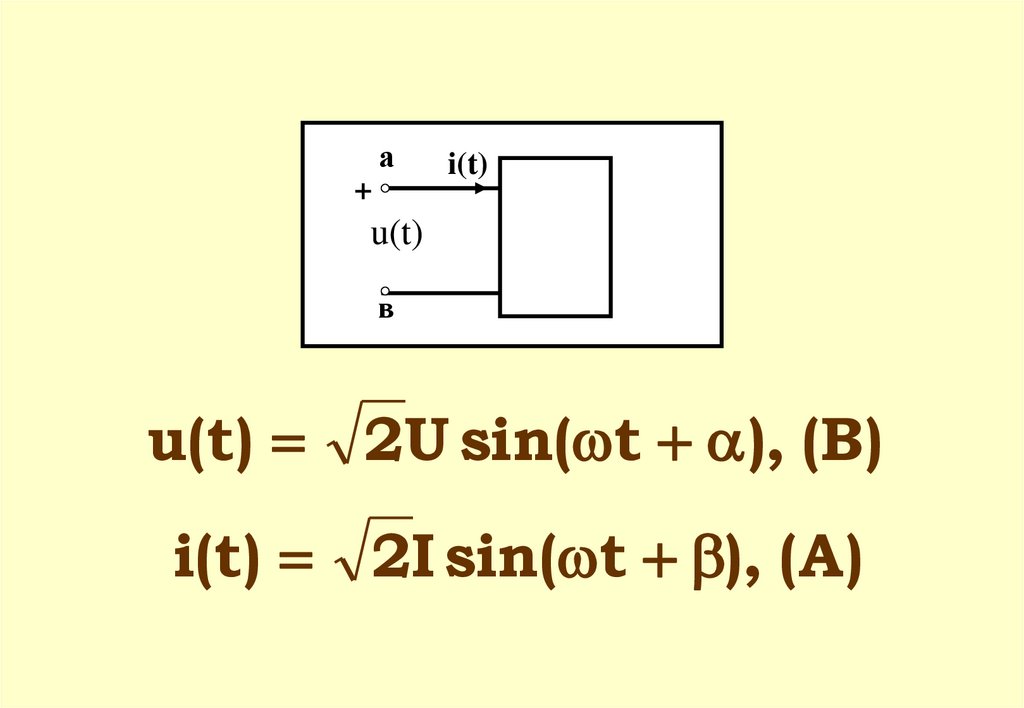
а+
i(t)
u(t)
в
u(t) 2U sin( t ), (B)
i(t) 2I sin( t ), (A)
47.
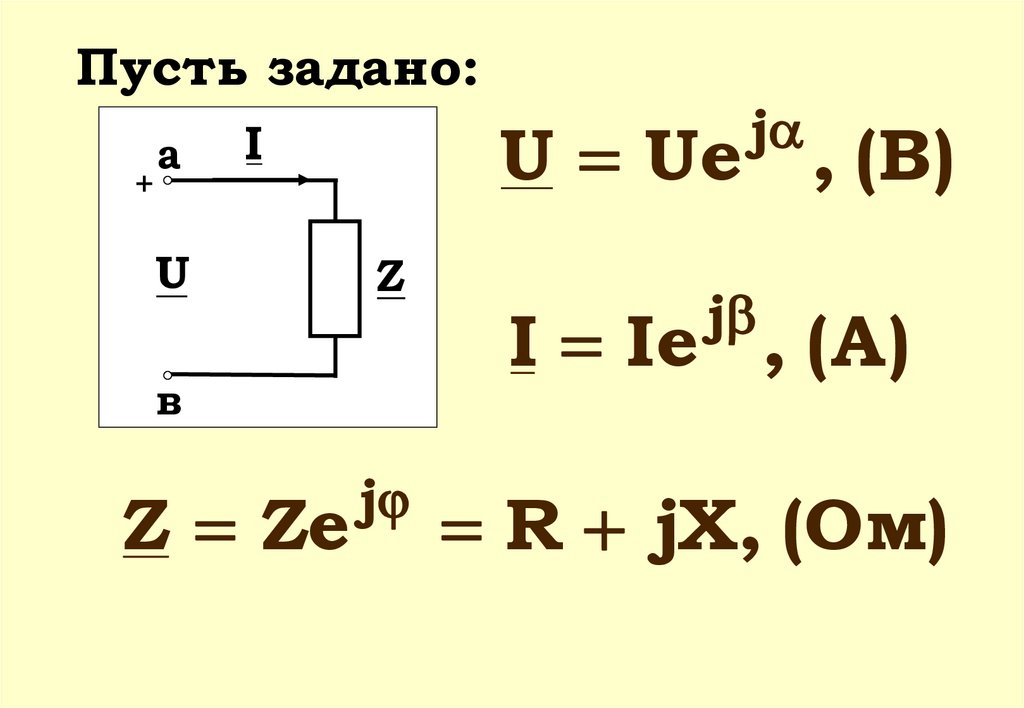
Пусть задано:+
а
U
Z
в
Z Ze
j
U Ue , (В)
I
j
j
I Ie , (A)
R jX, (Ом)
48.
ПриI Ie
j
находим
S U I P jQ , ( ВА)
- комплекс полной мощности
где
I Ie
j
-сопряженное
значение тока
49.
Т.к.U ZI
, то
S U I (Z I ) I
Z I I R jI X , ( ВА)
2
2
2
50.
Таким образомактивная мощность:
2
P UI cos I R, (Вт)
- это мощность тепловой
энергии
51.
Реактивная мощность:Q UI sin I X, (вар)
2
- пропорциональна
максимальной энергии,
запасаемой в электромагнитном
поле
52.
Полная мощность:P
S UI
, (ВА )
cos
-это максимально
возможная активная
мощность
при
cos 1
53.
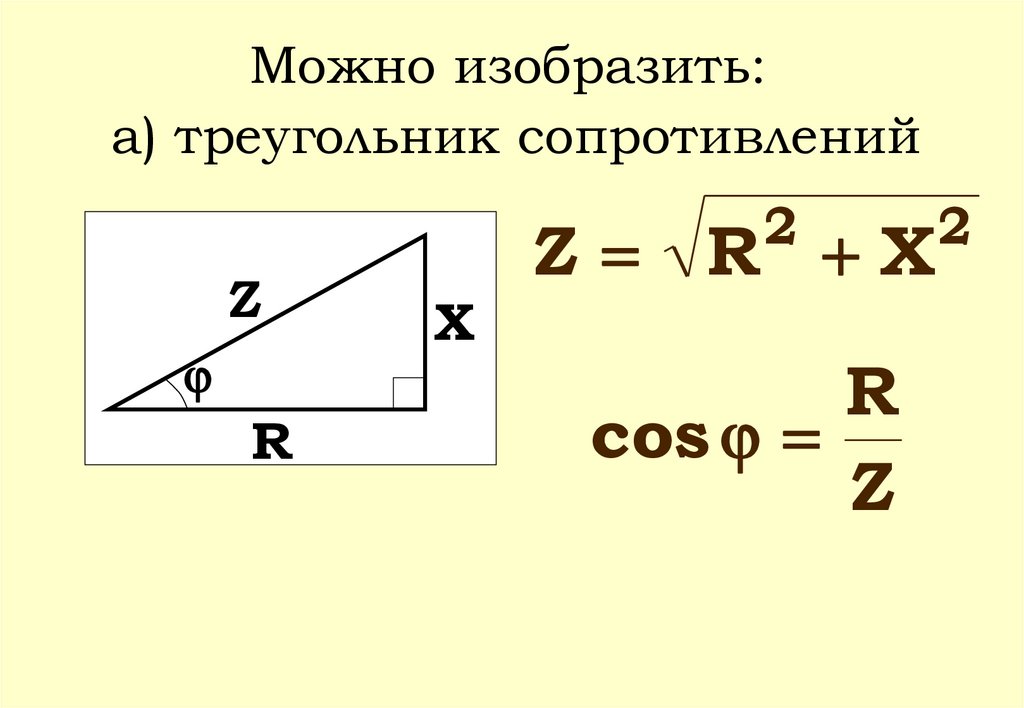
Можно изобразить:а) треугольник сопротивлений
2
Z
R
Z R X
Х
R
cos
Z
2
54.
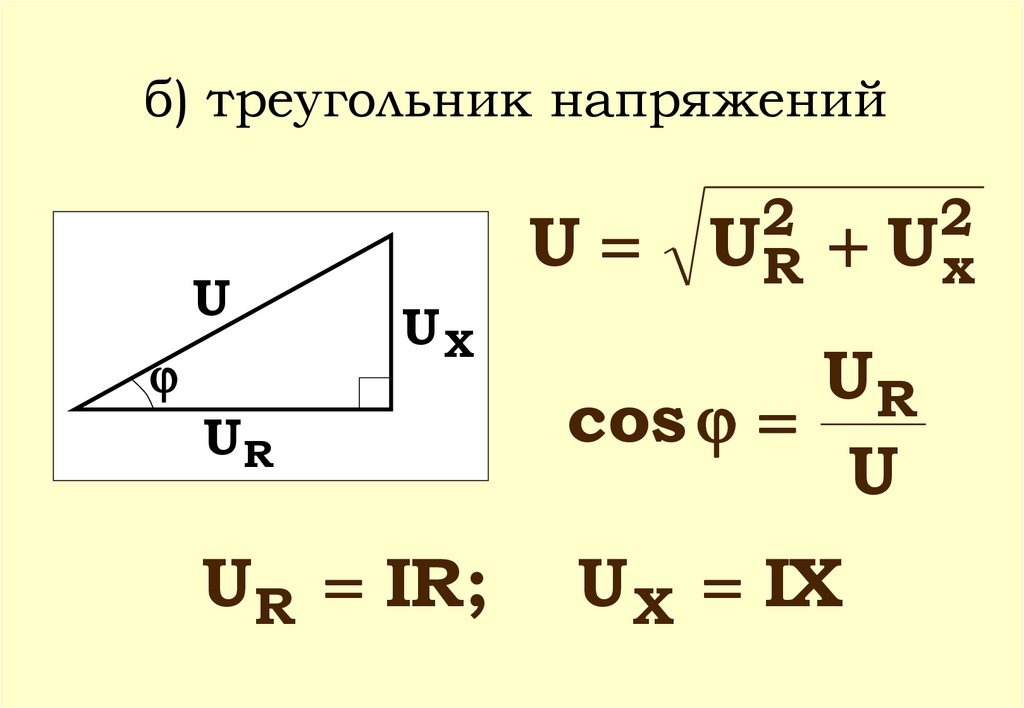
б) треугольник напряженийU
U
UХ
2
2
UR U x
UR
UR
cos
U
UR IR;
U X IX
55.
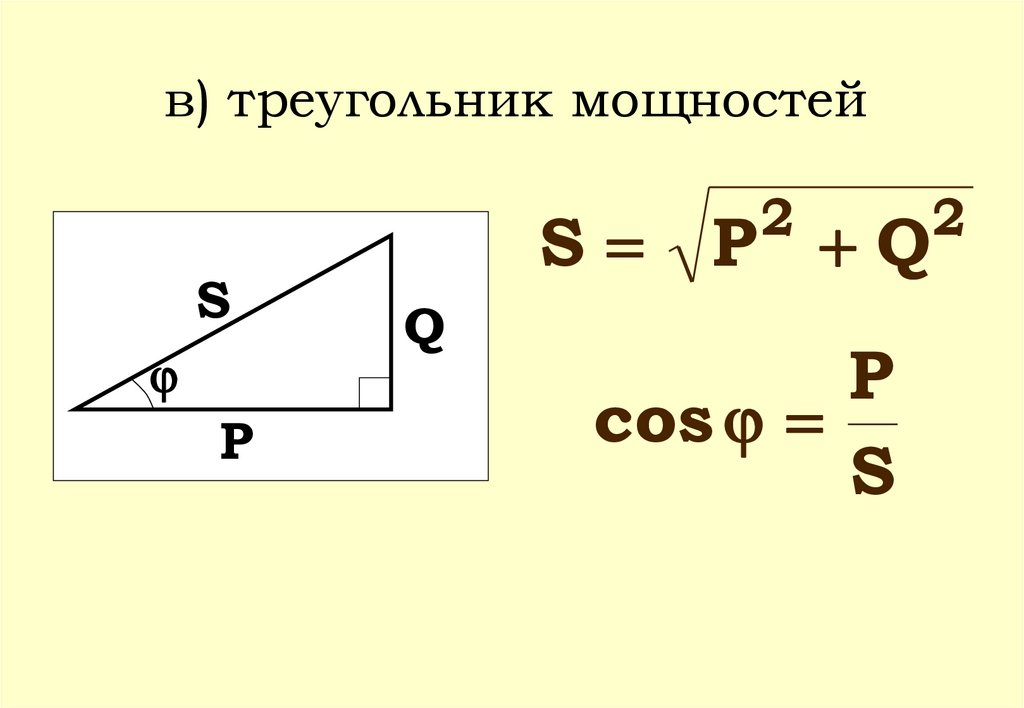
в) треугольник мощностей2
S
P
S P Q
Q
P
cos
S
2
56.
57.
Топографические и лучевыевекторные диаграммы
используются при анализе
и расчете цепей с синусоидальными напряжениями и токами
Эти диаграммы строятся
совмещенными на комплексной
плоскости в масштабах
напряжения и тока
58.
Лучевые векторные диаграммыстроятся
для комплексов действующих
значений токов, когда их
вектора выходят из начала
координат каждый под своим
углом
Эти диаграммы используются
для графической проверки
первого закона Кирхгофа
59.
Топографические векторныедиаграммы строятся для
комплексов действующих
значений напряжений, когда
их вектора подстраиваются
один к другому, образуя
замкнутые контуры
Эти диаграммы используются
для графической проверки
второго закона Кирхгофа
60.
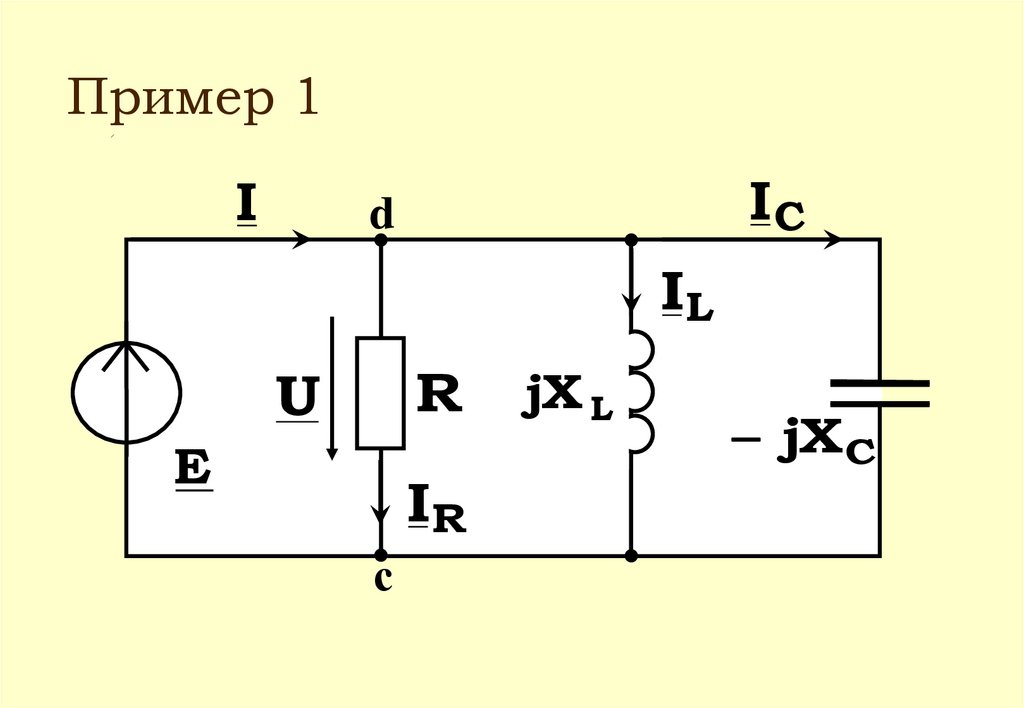
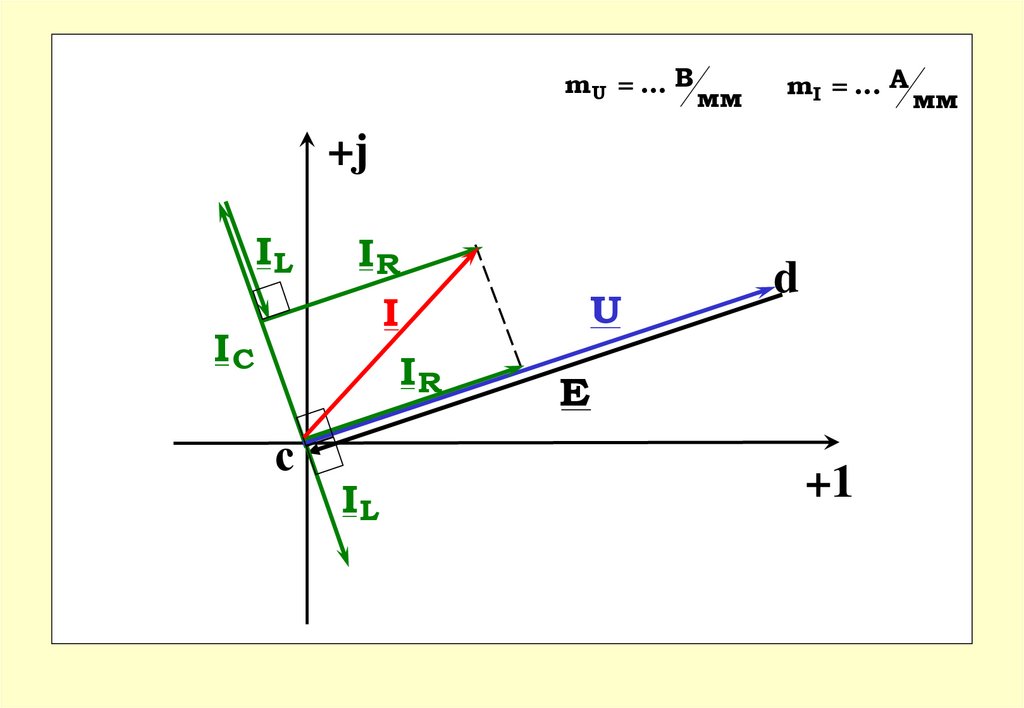
Пример 1I
IС
d
IL
R
U
E
IR
с
jX L
jX C
61.
m U ... Вмм
mI ... A
+j
IL
IR
I
IС
IR
с
IL
U
d
E
+1
мм
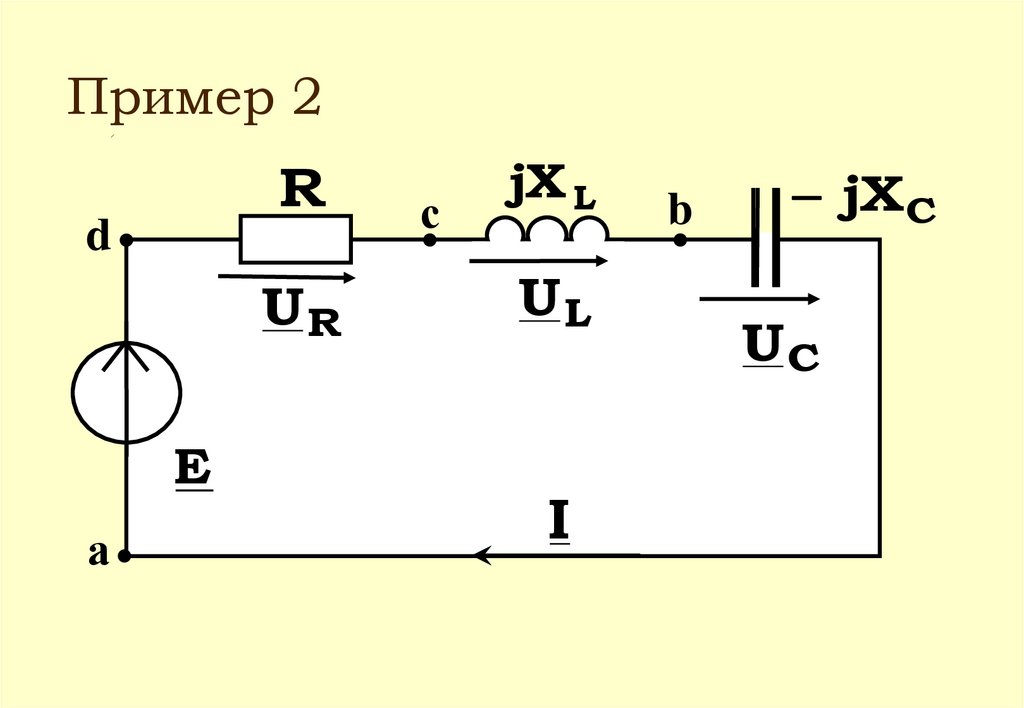
62.
Пример 2R
d
UR
E
а
с
jX L
UL
I
b
jX C
UС
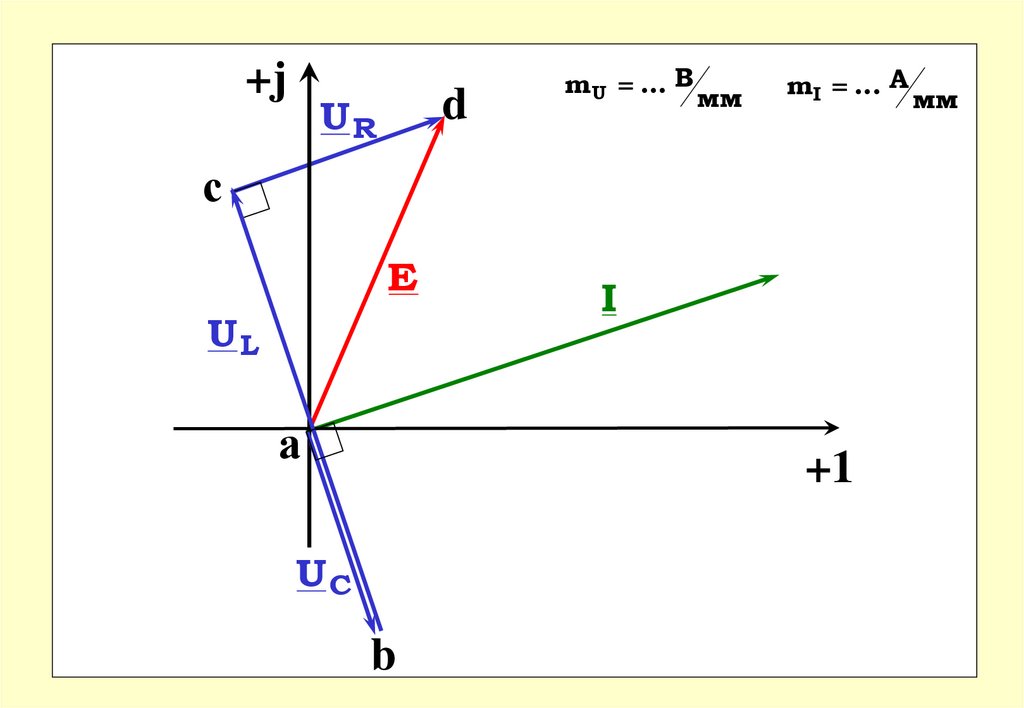
63.
+jd
UR
m U ... В
мм
mI ... A
с
E
UL
а
I
+1
UC
b
мм
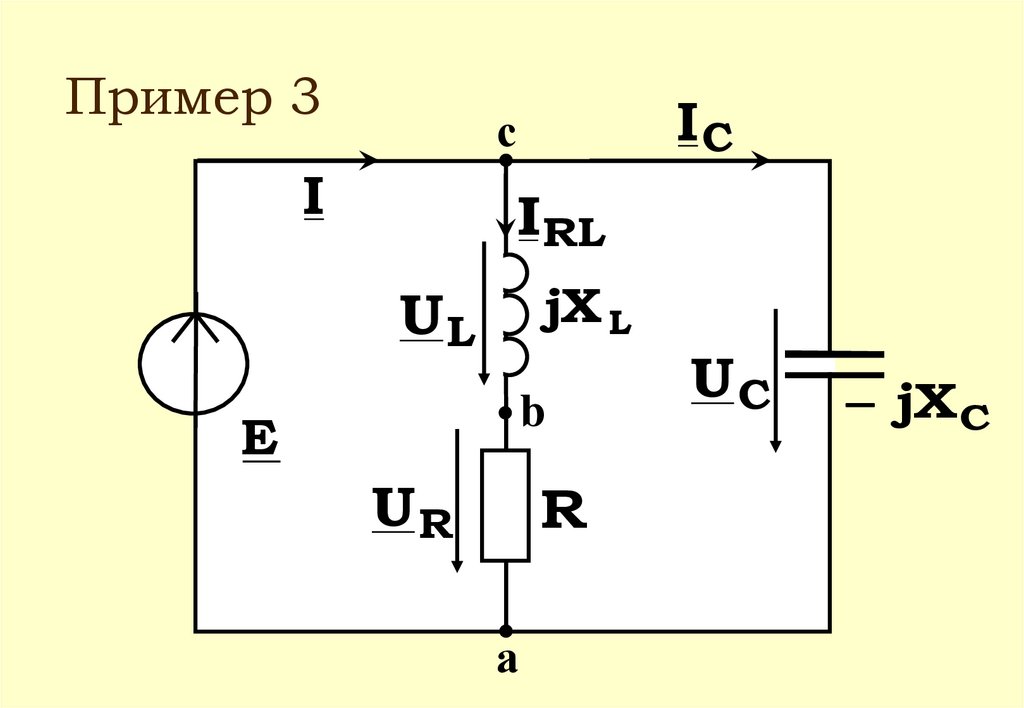
64.
Пример 3IС
с
I
IRL
jX L
UL
b
E
UR
R
а
UС
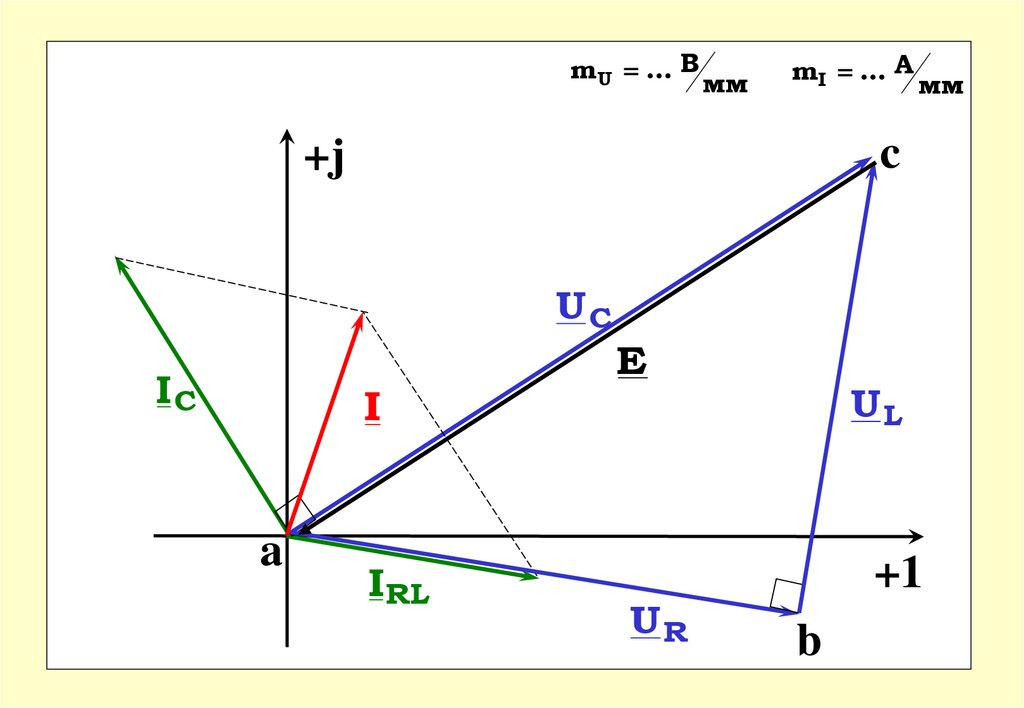
jX C
65.
m U ... Вмм
mI ... A
мм
c
+j
UС
IС
I
a
IRL
E
UR
UL
+1
b




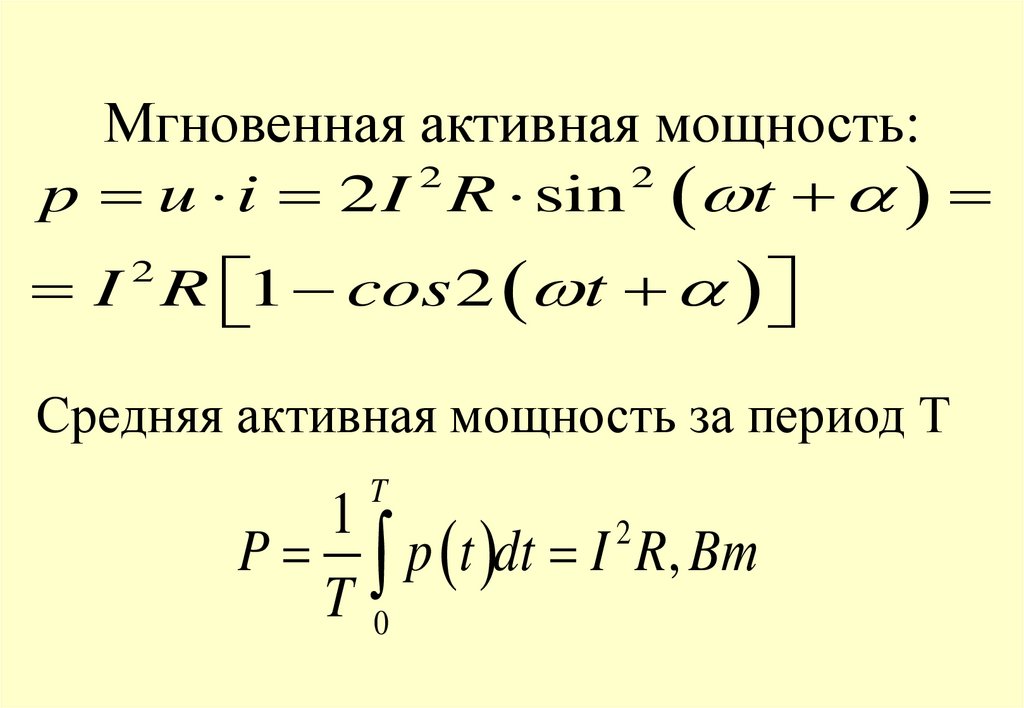


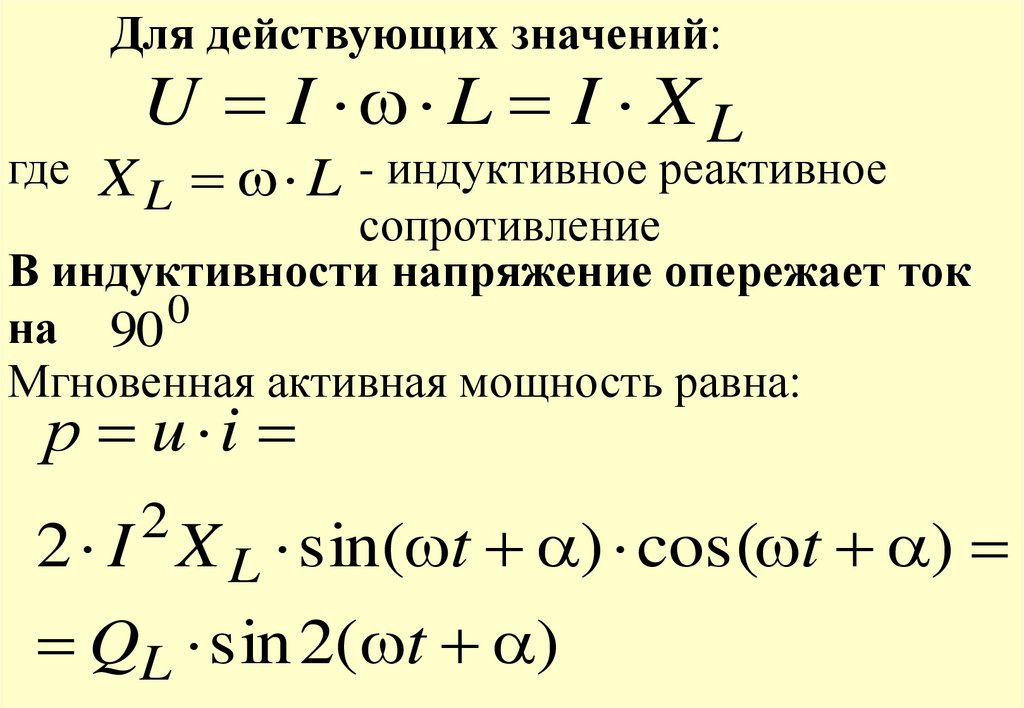


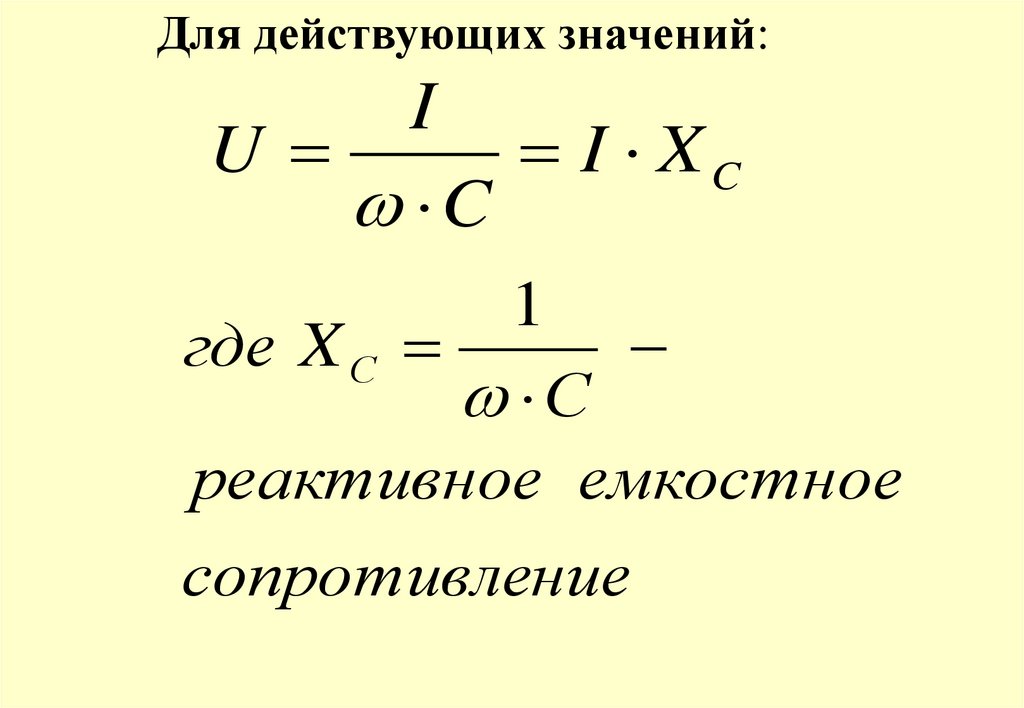





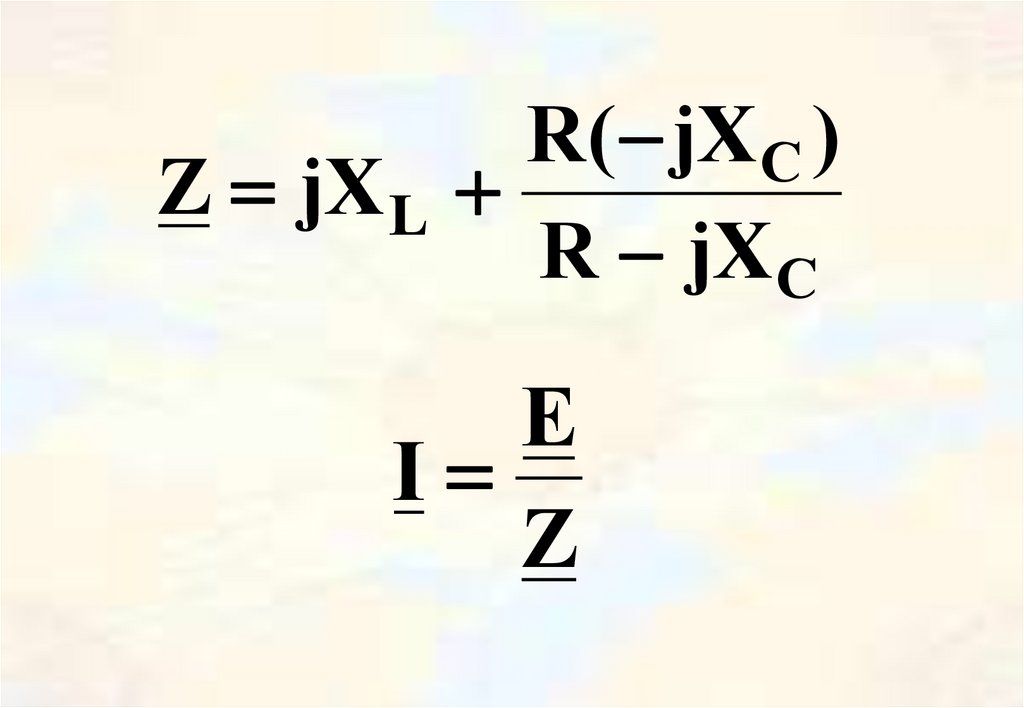





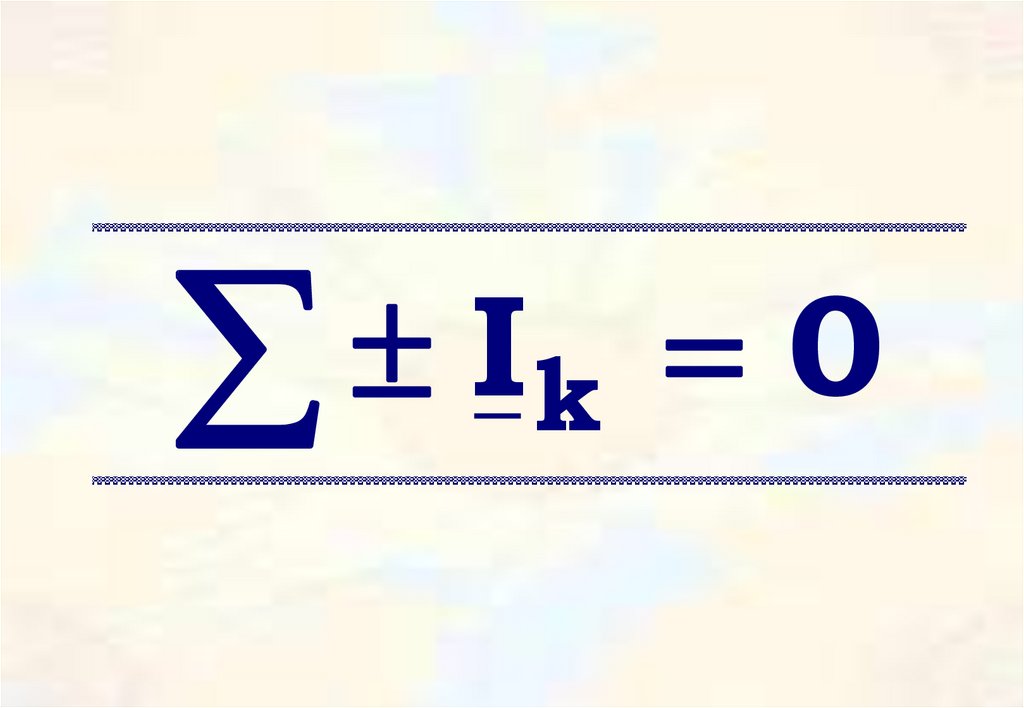


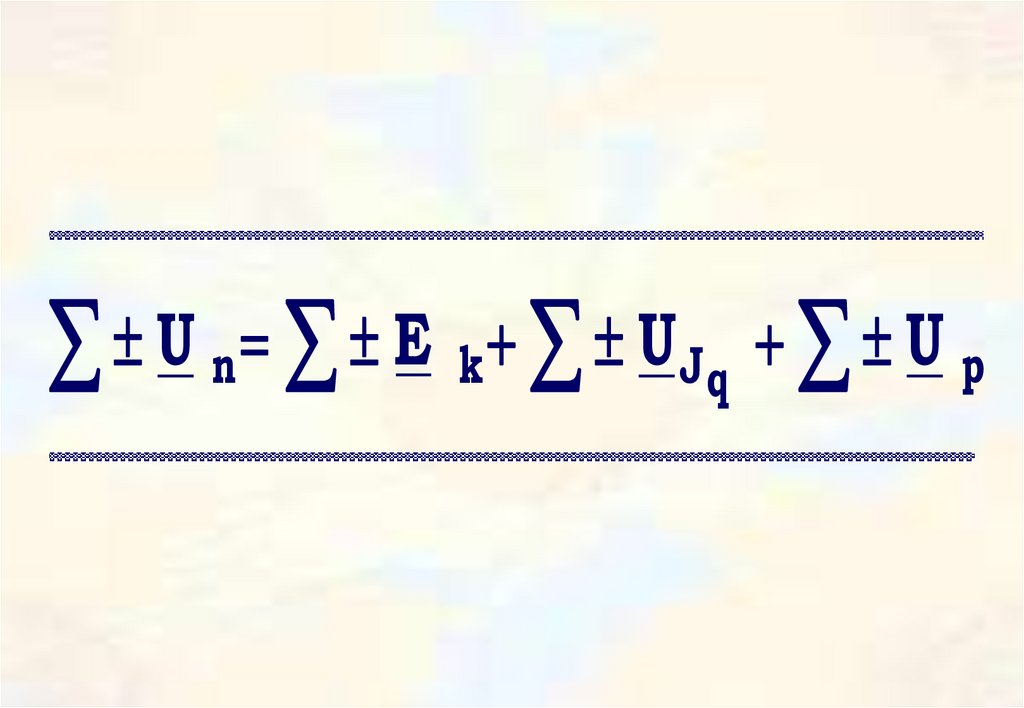
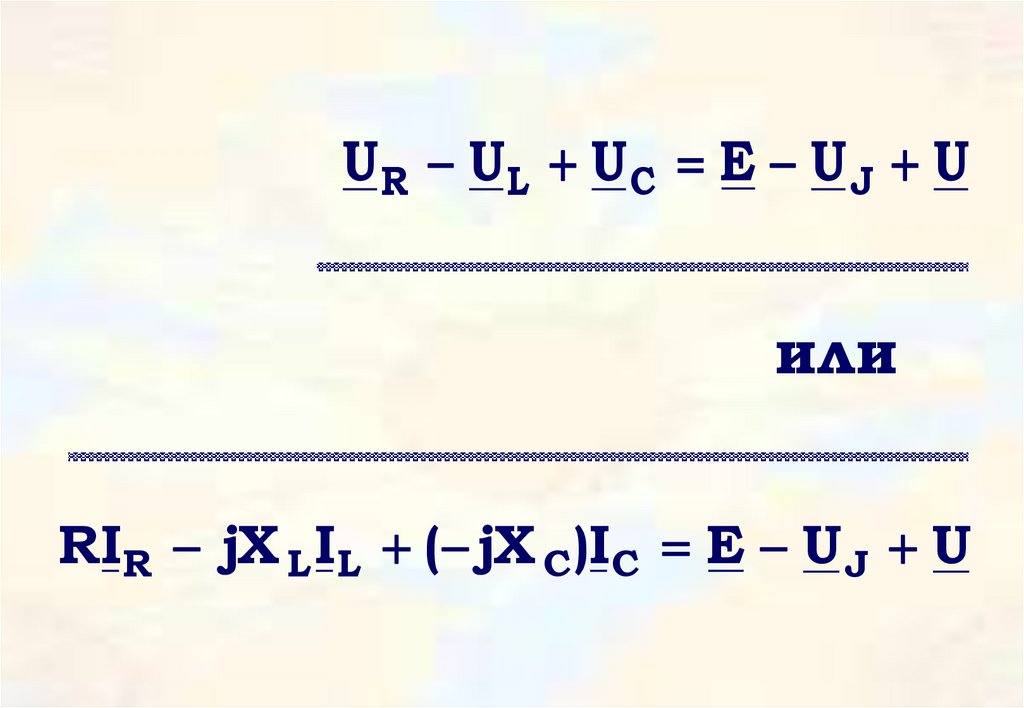


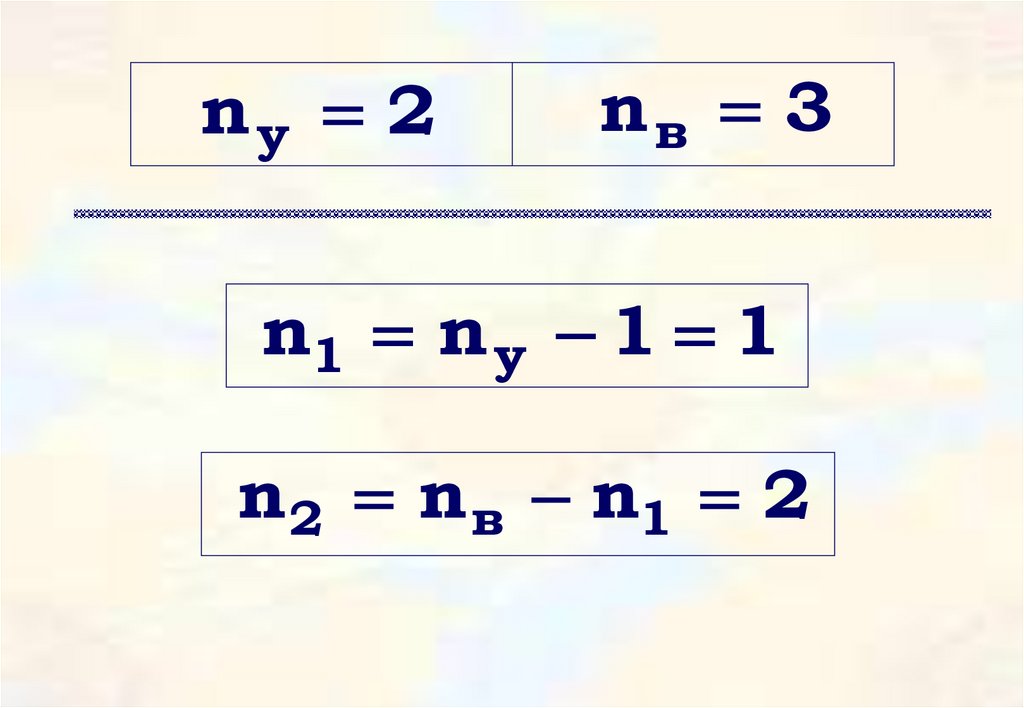
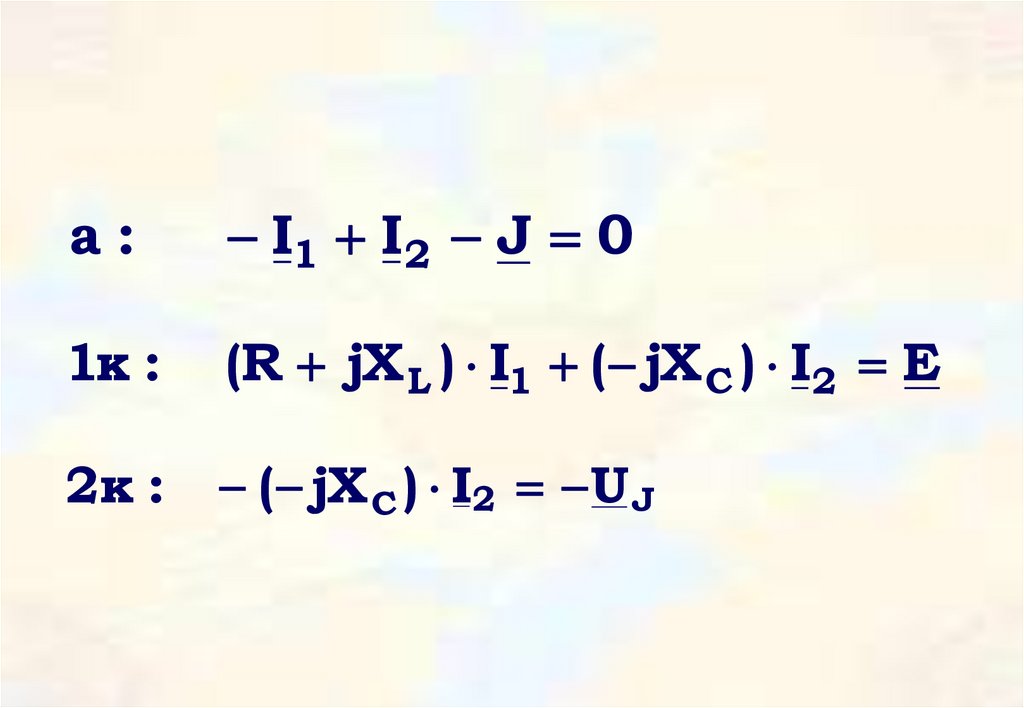
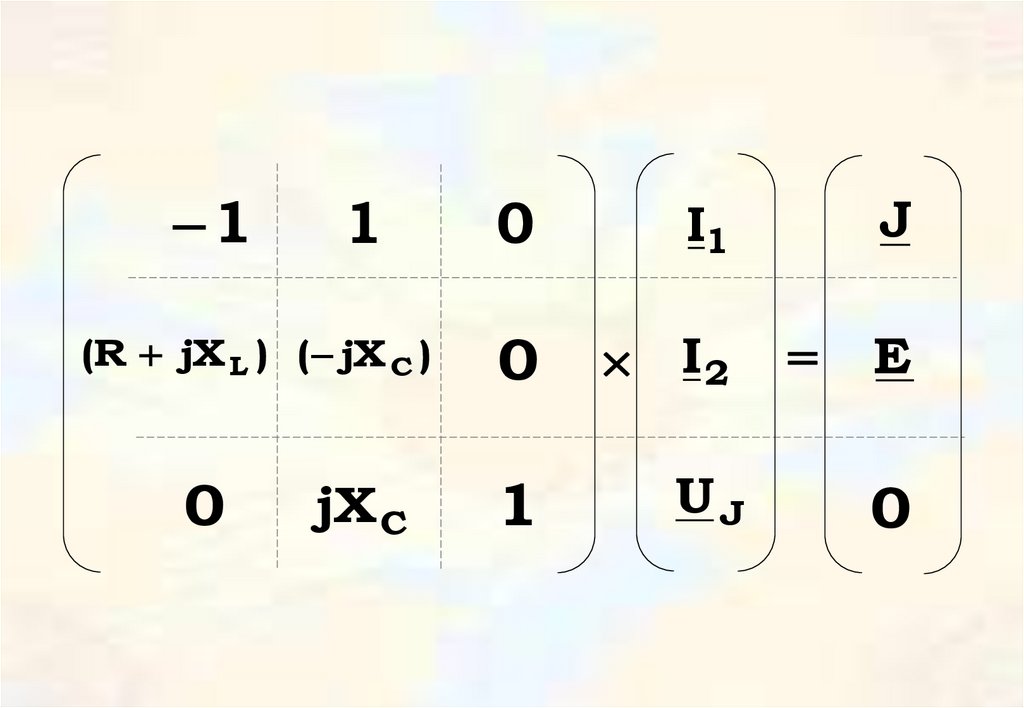



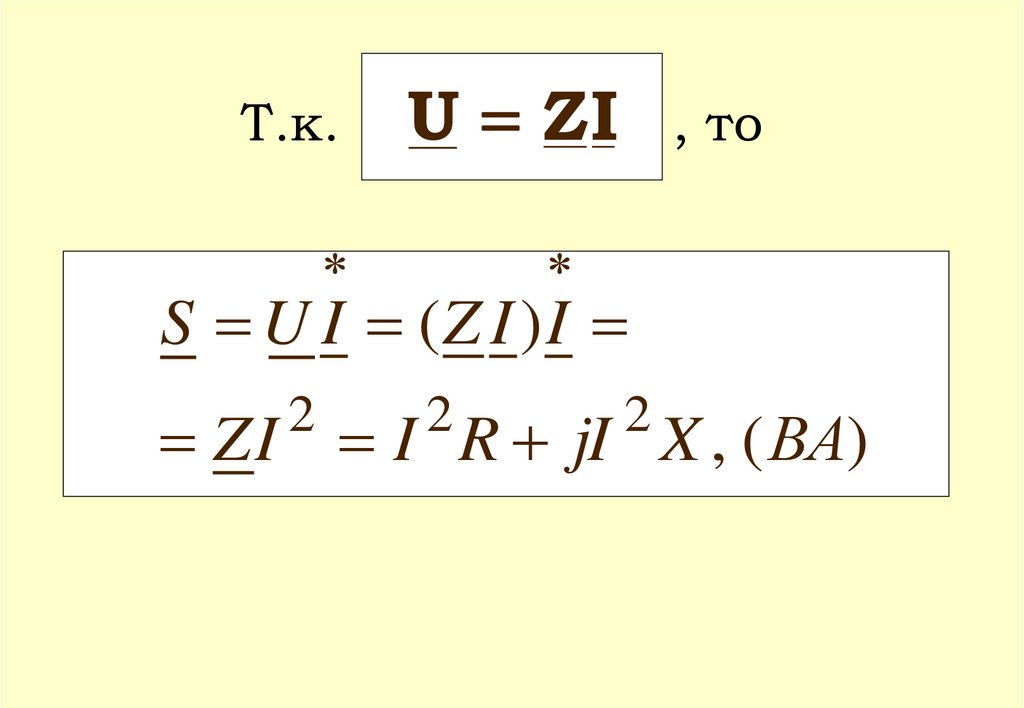







 physics
physics








