Применение комплексных чисел к расчету электрических цепей переменного тока. Лекция 6

1. БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова кафедра электротехники, О8

Лекция 6
Применение комплексных чисел к расчету
электрических цепей
переменного тока
1

2.

Расчёт электрической цепи классическим методом
Найти токи в ветвях и напряжения на элементах. Проверить баланс мощностей
а
Даны:
e(t ) 180 sin(314t 30 )
r1 40 Ом r2 20 Ом r3 30 Ом
x L 30 Ом xC 40 Ом
II
I
Вычислим комплекс действующего ЭДС:
180 j 30
E
e
127,3e j 30
2
b
127,3 cos 30 j127,3 sin 30
110,2 j 63,65
Выберем направления токов I1, I2, I3 в ветвях
Составим систему уравнений по законам Кирхгофа
Система уравнений в матричном виде:
I 1
r1 (r2 jxL )
0
. I 2
0 (r2 jxL ) (r3 jxC ) I 3
I 1 I 2 I 3 0
I 1r1 I 2 (r2 jx L ) E
I 2 (r2 jx L ) I 3 (r3 jxC ) 0
Решение ищем в виде
I A
1
1
E
1
1
0
E
0
2

3.

Расчёт электрической цепи классическим методом
Система перепишем в матричном виде:
I 1
40 (20 j 30)
0
I 2
0 (20 j 30) (30 j 40) I 3
1
1
1
0
E
Решение ищем в виде:
Решение:
I A
1
E
0
|I|=
|A|
Токи в ветвях:
I 1 1.565 0.671i
I 1.582 0.533i
2
I 3 0.018 1.204i
|I|
|E|
Напряжение на элементах ветвей:
U r1 I 1 Z1 (1.565 j 0.671) 40 62,6 j 26,84 68,11e j 23
U r2 I 2 r2 (1.582 j 0.533) 20 31,64 j10,66 33,4e j19
U xL I 2 xL (1.582 j 0.533) j 30 15,99 j 47,46 50,1e j 71
j 91
U r3 I 3 r3 (-0.018 j1.204) 30 0,54 j 36,12 36,122e
j1
U xC I 3 xC (-0.018 j1.204) ( j 40) 48,16 j 0,72 48,161e
U ab
Напряжение между узлами а и b:
j 38
U r2 U xL 31,64 j10,66 15,99 j 47,46 47,63 j 36,8 60,2e
3

4.

Расчёт электрической цепи методом эквивалентных преобразований
Обозначим комплексы сопротивлений:
Z1 r1
Z 2 r2 jx L 20 j 30
а
Z 3 r3 jxC 30 j 40
Z 23
(r2 jx L )(r3 jxC )
r2 jx L r3 jxC
b
(20 j 30)(30 j 40)
34,23 j8,85
20 j 30 30 j 40
Вычислим токи в ветвях по закону Ома:
E
110,2 j 63,65
j 23
1.565 0.671i 1,71e
Z1 Z 23 34,23 j8,85
j 37
I Z (1.565 j 0.671) (34,23 j8,85) 47.619 j 36.809 B 60,2e
I 1
U ab
1
23
U
I ab 47,62 j 36,81 1.582 j 0.533 1,57e j19
2
Z2
20 j 30
I U ab 47,62 j 36,81 0.018 j1.204 1,2041e j 91
3
Z3
30 j 40

5.

Проверка результатов векторной форме:
+j
U r1 68e j 23
U r2 36e j 91
U 33,4e j19
U xL
r2
U xL 50,1e j 71
j1
U xC 48e
U ab 60,2e j 37 `
E 127,3e j 30
I 1 1.565 0.671i
I 1.582 0.533i
2
I 3 0.018 1.204i
U ab U r2 U xL U r3 U xC
U ab
U r2
U r1
I 3
I 1
0
I 2
U xC
+1
U r2
I 1 I 2 I 3
5

6.

Баланс мощностей
Полная мощность источника:
Полная мощность потребителей:
*
S ист E I
E комплекс ЭДС источника
S пр I12 r1 I 22 r2 I 22 ( jx L ) I 32 r3 I 32 ( jxC )
*
I - сопряженный тто ветви с ЭДС
S пр 1,712 40 1,57 2 20 1,57 2 j 30
S 127,3e j 30 1,71e j 23 217,7e j 7
215 j 26 ВА
P 215 Вт;
Q 26 ВАр
1,204 2 30 1,204 2 j 40 209,8 j15,96
Pпр 209,8 Вт;
Qпр 15,96 ВАр;
S ист S пр
6

7.

Резонанс
1.
2.
Резонанс напряжений
Резонанс токов
Резонанс – явление в электрической цепи, когда напряжения и токи
на элементах электрической цепи превышает приложенное синусоидальное
воздействие во много раз.
Рассмотрим резонанс напряжений в простой электрической цепи с последовательным
соединением RLC
При резонансе двухполюсник от сети потребляет только активную мощность!
Потребляемая реактивная мощность равно нулю! Следовательно, реактивное
сопротивление x равно нулю.
7

8.

Резонанс
Входное воздействие
u (t ) U m sin( t )
U
Составим второй закон Кирхгофа
1
U U r U L U C I (r jx L jxC ) I (r j ( x L xC )) I (r j ( L
))
C
При резонансе x=xL-xC=0 Следовательно: x= L-1/ C=0
Отсюда найдем собственную
частоту колеб. контура:
0 L
1
или 0
0C
1
LC
Резонанс можно достичь изменяя , L, C.
При резонансе фазовый сдвиг между входным током напряжением равен 0.
x L xC
arctg
0
r
8

9.

Резонанс
При резонансе:
U L IxL U C IxC
U x U L UC 0
U r Ir U
U L UC
Векторная диаграмма:
U L
U r
U C
I
U U r
Ток при резонансе имеет макс. значение: I
U
U
U
2
z
r ( x L xC ) r

10.

Резонанс
Сопротивления реактивных элементов xL и xC при резонансе называются
реактивным сопротивлением
1
L
C
Для колебательного контура вводится понятие Добротность Q:
Q
U C0
U
U L0
U
r
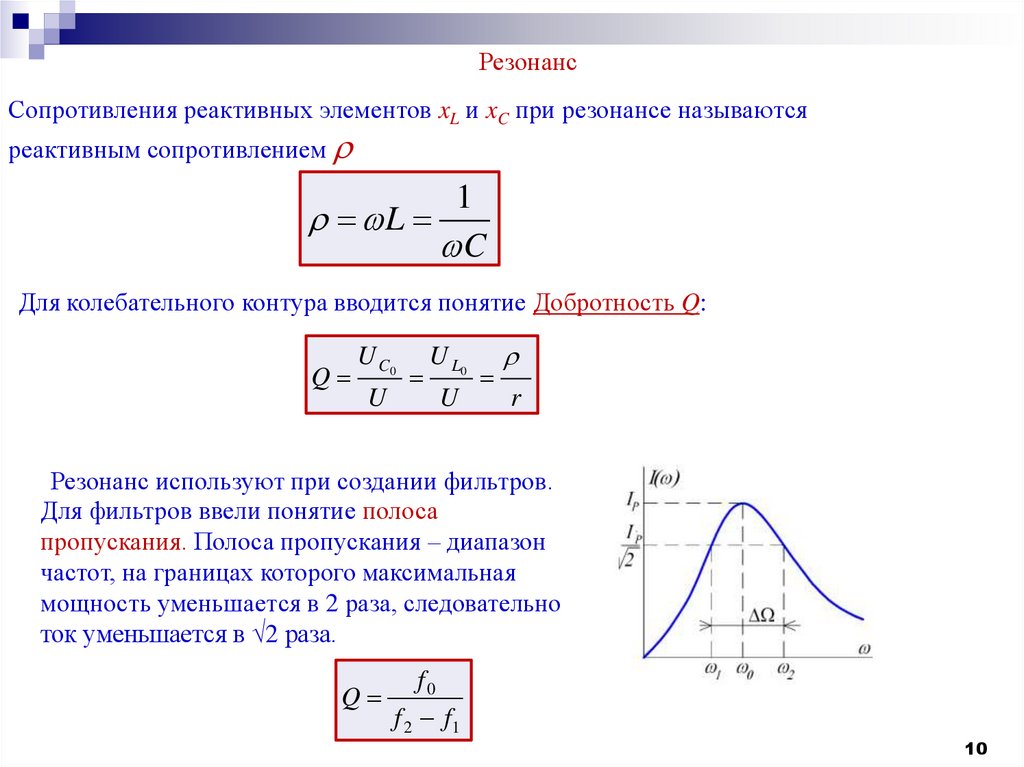
Резонанс используют при создании фильтров.
Для фильтров ввели понятие полоса
пропускания. Полоса пропускания – диапазон
частот, на границах которого максимальная
мощность уменьшается в 2 раза, следовательно
ток уменьшается в 2 раза.
Q
f0
f 2 f1
10