Similar presentations:
Электрические цепи переменного тока. Лекция 2
1. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
2.
Основные параметрыi( t) I m sin( t i ) е( t) Еm sin( t е ) и( t) U m sin( t u )
где Im (Em, Um) – амплитуда (то есть наибольшее значение) тока (э.д.с.,
напряжения);
i(t) – мгновенное значение тока (э.д.с. е, напряжения u);
(ωt ± ψ) – аргумент синусоиды, фаза, или фазовый угол;
ω – угловая частота (рад/с), скорость изменения угла, ω=2πf.
В России ω = 2∙3,14∙50 = 314 рад/с;
t – время, (с);
ψ – начальная фаза, или фаза смещения. Она определяется
величиной смещения синусоиды относительно начала координат.
2
3.
Действующие значения тока, э.д.с., напряженияДействующим значением переменного тока называется такой постоянный ток,
который на одном и том же резисторе сопротивлением R за то же время
выделяет столько же тепла, что и данный переменный ток.
1 T 2
I
i dt
T 0
Действующие значения токов, э.д.с., напряжений
Im
I
0,707 I m
2
Амплитудные значения
Еm
Е
0,707 Еm
2
Im 2I
Um
U
0,707U m
2
Em 2 E U m 2U
3
4.
Среднее значение тока, э.д.с., напряженияСреднее (то есть среднеарифметическое значение) переменного тока – это
значение тока за половину периода, в течение которого его знак не меняется
I ср
I ср
2
idt
T 0
2I m
T
2
0,637 I m
Аналогично для э.д.с. и напряжения:
Eср = 0,637Em, Uср = 0,637Um.
4
5.
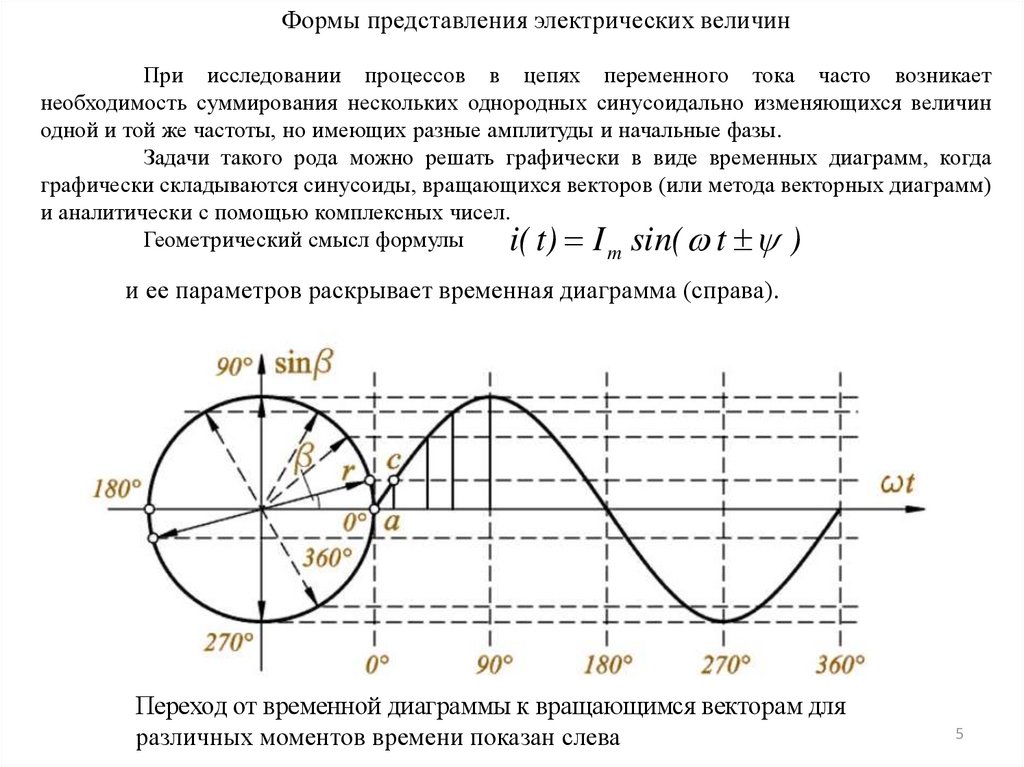
Формы представления электрических величинПри исследовании процессов в цепях переменного тока часто возникает
необходимость суммирования нескольких однородных синусоидально изменяющихся величин
одной и той же частоты, но имеющих разные амплитуды и начальные фазы.
Задачи такого рода можно решать графически в виде временных диаграмм, когда
графически складываются синусоиды, вращающихся векторов (или метода векторных диаграмм)
и аналитически с помощью комплексных чисел.
Геометрический смысл формулы
i( t) I sin( t )
m
и ее параметров раскрывает временная диаграмма (справа).
Переход от временной диаграммы к вращающимся векторам для
различных моментов времени показан слева
5
6.
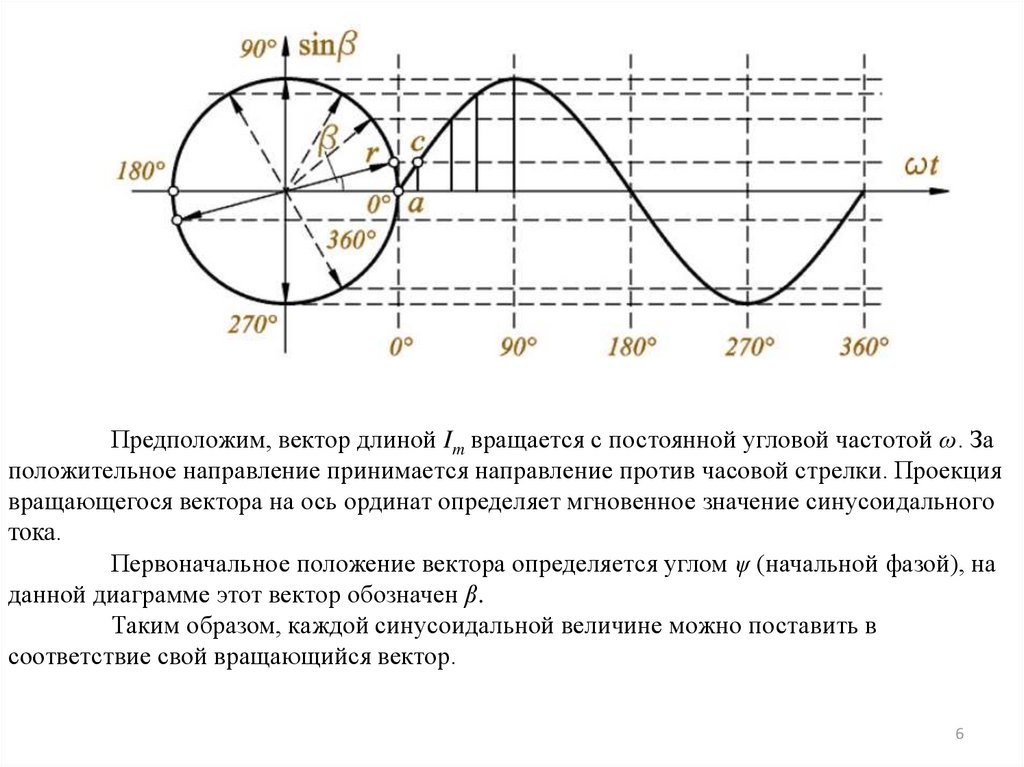
Предположим, вектор длиной Im вращается с постоянной угловой частотой ω. Заположительное направление принимается направление против часовой стрелки. Проекция
вращающегося вектора на ось ординат определяет мгновенное значение синусоидального
тока.
Первоначальное положение вектора определяется углом ψ (начальной фазой), на
данной диаграмме этот вектор обозначен β.
Таким образом, каждой синусоидальной величине можно поставить в
соответствие свой вращающийся вектор.
6
7.
При действиях с несколькимисинусоидами получаем несколько векторов,
действия над которыми заменяют действия
над синусоидальными токами или
напряжениями.
Векторы-амплитуды вращаются с
одинаковой скоростью, так как частота всех
токов и напряжений одна, а значит,
относительно друг друга они неподвижны.
Поэтому, когда диаграммы
используются для сложения действующих
величин напряжений и токов, то векторы не
вращают.
Таким образом, векторной диаграммой называется совокупность векторов,
характеризующих процесс в электрической цепи.
Векторные диаграммы бывают двух типов:
– лучевые;
– топографические.
Лучевой диаграммой называется диаграмма, в которой все векторы напряжений и
токов цепи строят из одной точки.
Топографической диаграммой называется диаграмма, на которой векторы
напряжений пристраиваются друг к другу в том же порядке, в котором они действуют в
электрической цепи.
7
Чаще применяются топографические диаграммы.
8.
Метод комплексных чисел(cos j sin ) e j формулаЭйлера
с а jb
- алгебраическая форма записи комплексного числа
с
– комплексное число
а Re c – действительная (реальная) часть комплексного числа
b Im c – мнимая часть комплексного числа
j – мнимая единица, или оператор поворота на 90º в положительную стороны (против
часовой стрелки)
с а jb
с а jb – сопряженные комплексные числа
а c cos
b c sin
с c(cos j sin )
с ce
j
– показательная форма записи
с а2 b2
аrctg
b
a
– тригонометрическая форма записи
(jψ – поворотный множитель)
– модуль комплексного числа
– аргумент комплексного числа
8
9.
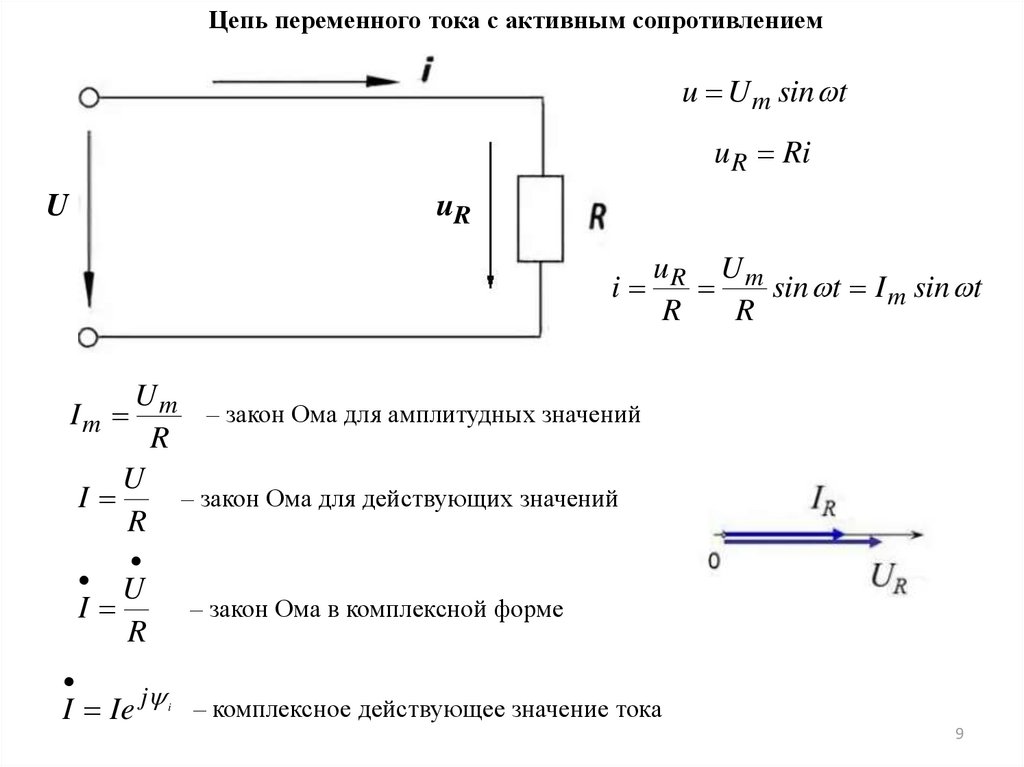
Цепь переменного тока с активным сопротивлениемu U m sin t
uR Ri
U
uR
uR U m
i
sin t I m sin t
R
R
U
I m m – закон Ома для амплитудных значений
R
U
– закон Ома для действующих значений
I
R
I
U
R
– закон Ома в комплексной форме
I Ie j – комплексное действующее значение тока
i
9
10.
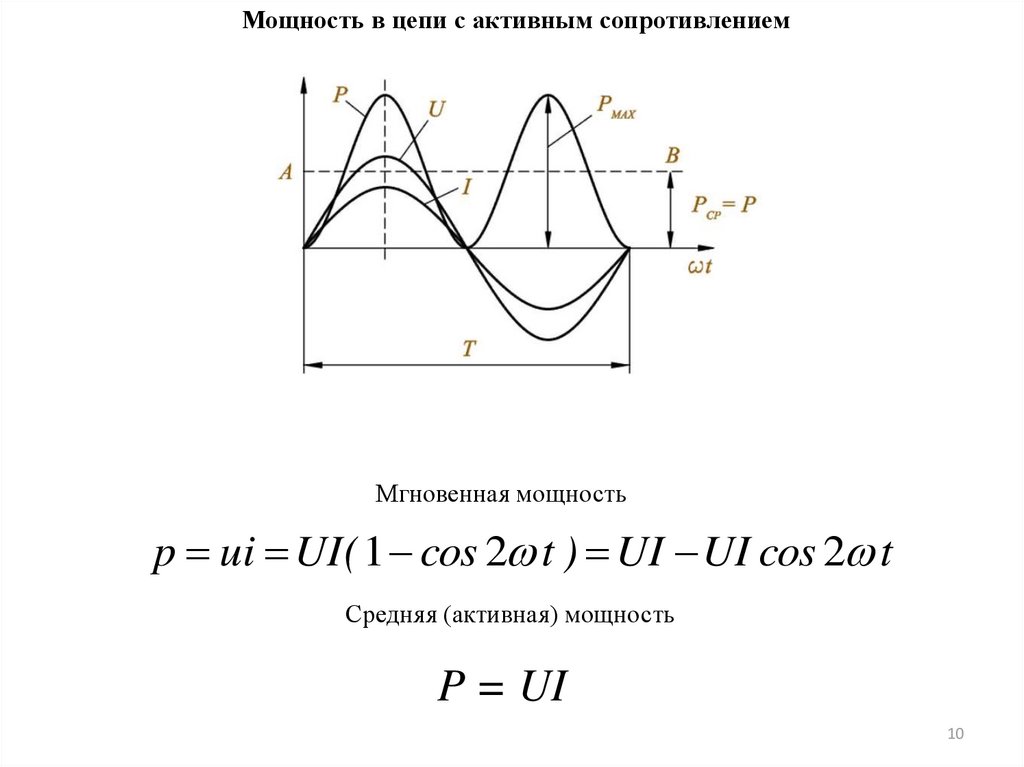
Мощность в цепи с активным сопротивлениемМгновенная мощность
p ui UI ( 1 cos 2 t ) UI UI cos 2 t
Средняя (активная) мощность
P = UI
10
11.
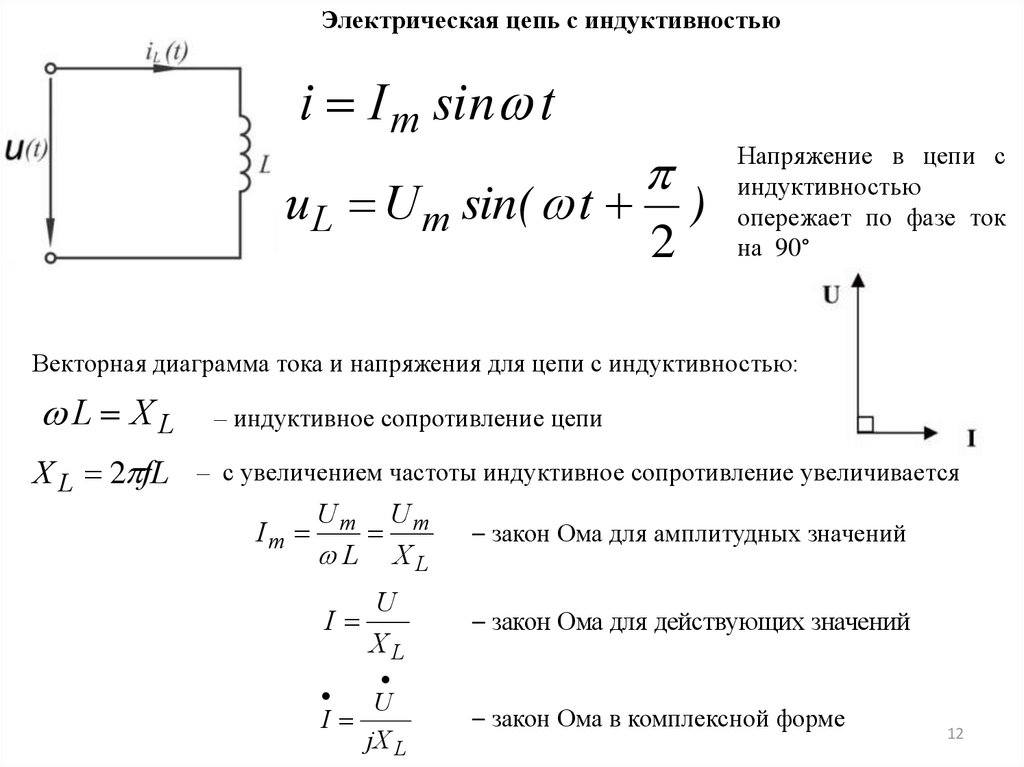
Электрическая цепь с индуктивностью, то
Под действием синусоидального напряжения в цепи
протекает синусоидальный ток
i I m sin t
В результате этого вокруг катушки возникает
.
переменное
магнитное поле, и в катушке
наводится э.д.с. самоиндукции.
Если R = 0, то напряжение источника целиком идет на уравновешивание этой э.д.с.
u L e L
По закону электромагнитной индукции
di
eL L
dt
d ( I m sin t )
di
uL L L
I m L cos t
dt
dt
или
u L U m sin( t
2
)
где
U m I m L
11
12.
Электрическая цепь с индуктивностьюi I m sin t
u L U m sin( t
2
)
Напряжение в цепи с
индуктивностью
опережает по фазе ток
на 90°
Векторная диаграмма тока и напряжения для цепи с индуктивностью:
L XL
X L 2 fL
– индуктивное сопротивление цепи
– с увеличением частоты индуктивное сопротивление увеличивается
Um Um
Im
L XL
I
I
– закон Ома для амплитудных значений
U
XL
– закон Ома для действующих значений
U
jX L
– закон Ома в комплексной форме
12
13.
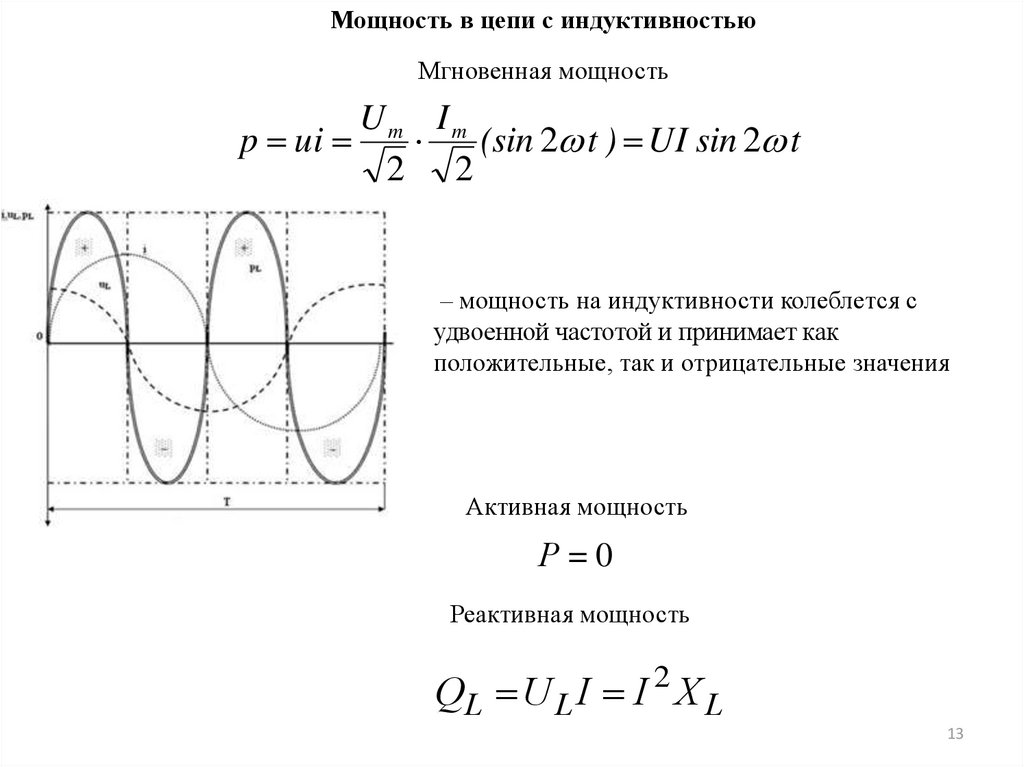
Мощность в цепи с индуктивностьюМгновенная мощность
Um Im
p ui
(sin 2 t ) UI sin 2 t
2 2
– мощность на индуктивности колеблется с
удвоенной частотой и принимает как
положительные, так и отрицательные значения
Активная мощность
Р=0
Реактивная мощность
QL U L I I 2 X L
13
14.
Электрическая цепь с емкостьюi I m sin t
Im
uC U mC sin( t ) U mC
C
2
– амплитудное значение
напряжения на емкости
1
1
X C – емкостное сопротивление
C 2 f C
Ток опережает напряжение на емкости на 90°, так как напряжение
на обкладках конденсатора появляется только после
возникновения тока
Im
Um
XC
– закон Ома для амплитудных значений
I
U
XC
– закон Ома для действующих значений
I
U
jX C
– закон Ома в комплексной форме
14
15.
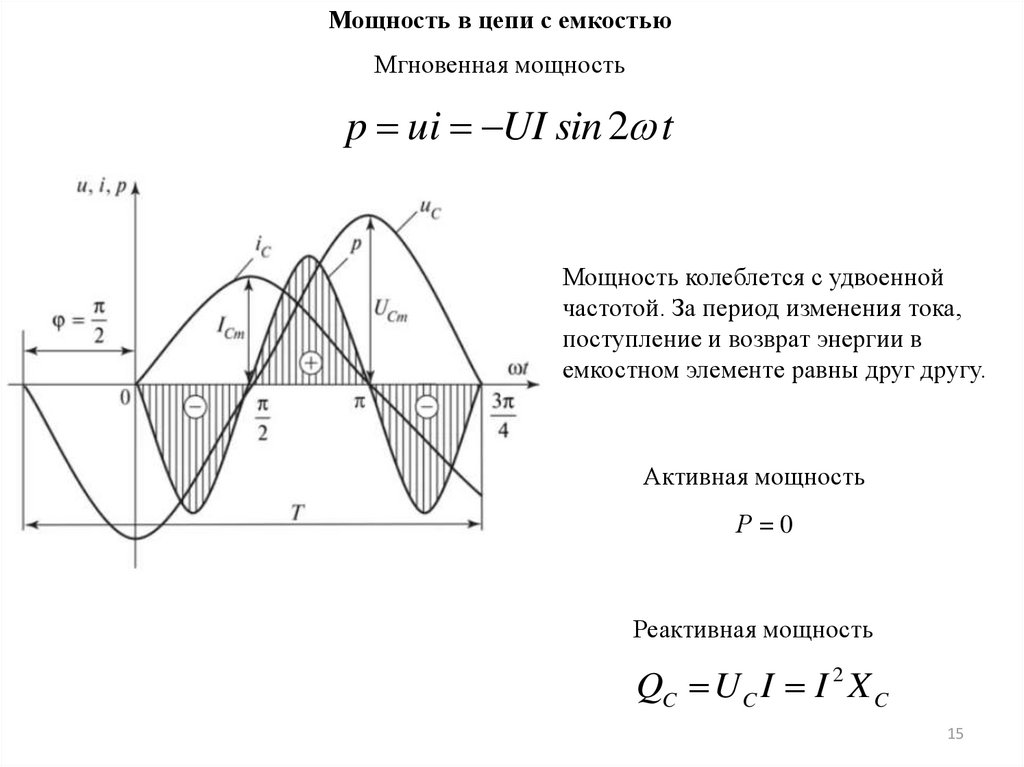
Мощность в цепи с емкостьюМгновенная мощность
p ui UI sin 2 t
Мощность колеблется с удвоенной
частотой. За период изменения тока,
поступление и возврат энергии в
емкостном элементе равны друг другу.
Активная мощность
Р=0
Реактивная мощность
QC U C I I 2 X C
15
16.
Правила Кирхгофа для цепей переменного токаn
Ii
i 1
Первое правило Кирхгофа
0
Алгебраическая сумма комплексных токов в узле электрической цепи равна нулю
Второе правило Кирхгофа
n
Еi
i 1
m
m
U i I i Z i
i 1
i 1
Алгебраическая сумма комплексных значений э. д. с. в любом контуре
электрической цепи равна алгебраической сумме комплексных значений падений
напряжений на всех приемниках этого контура
Правила Кирхгофа справедливы для мгновенных значений токов, э. д. с., напряжений
16
17.
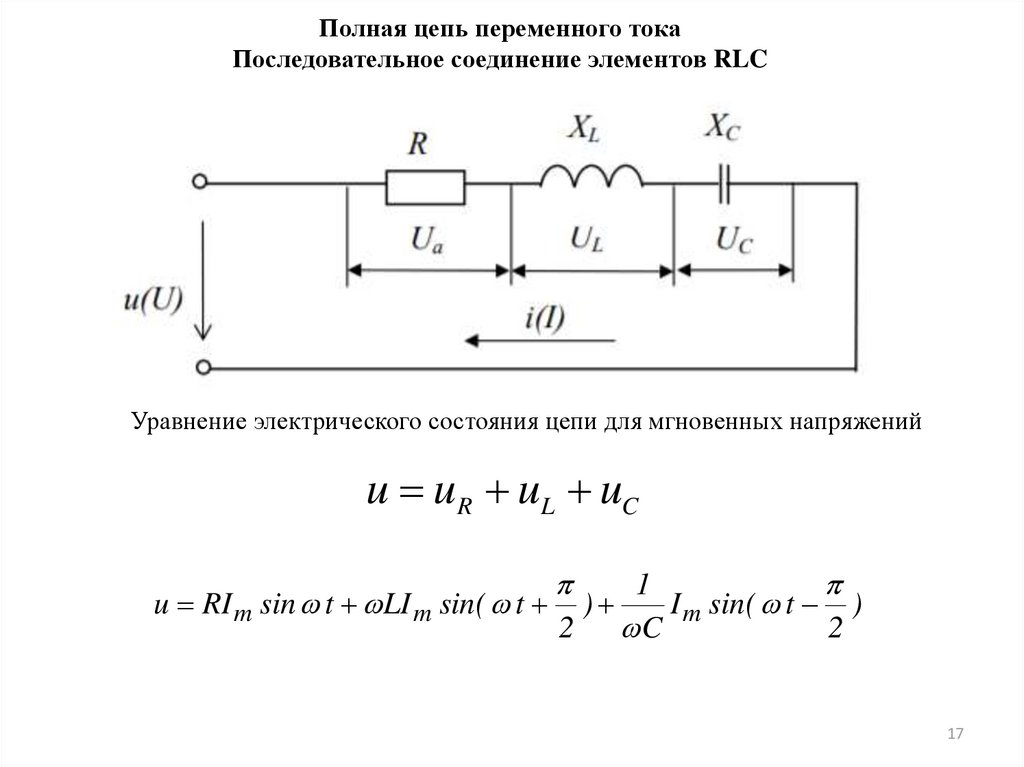
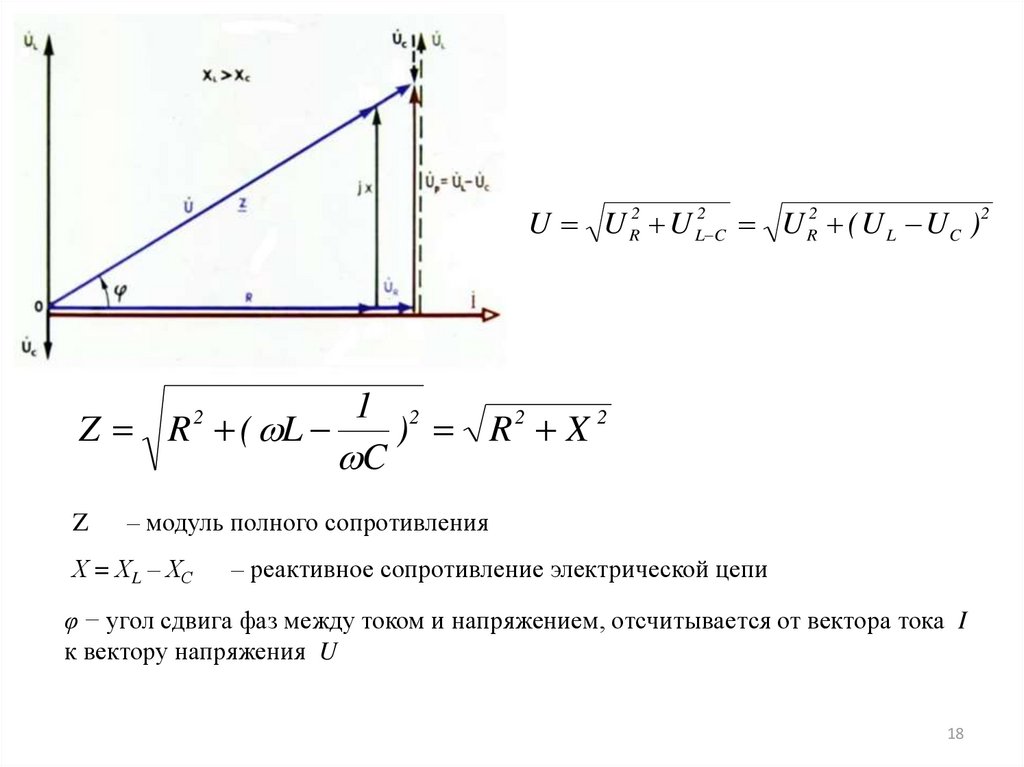
Полная цепь переменного токаПоследовательное соединение элементов RLC
Уравнение электрического состояния цепи для мгновенных напряжений
u uR uL uC
u RI m sin t LI m sin( t
2
)
1
I m sin( t )
C
2
17
18.
U U R2 U L2 C U R2 ( U L U C )21 2
Z R ( L
) R2 X 2
C
2
Z
– модуль полного сопротивления
Х = ХL – ХС
– реактивное сопротивление электрической цепи
φ − угол сдвига фаз между током и напряжением, отсчитывается от вектора тока I
к вектору напряжения U
18
19.
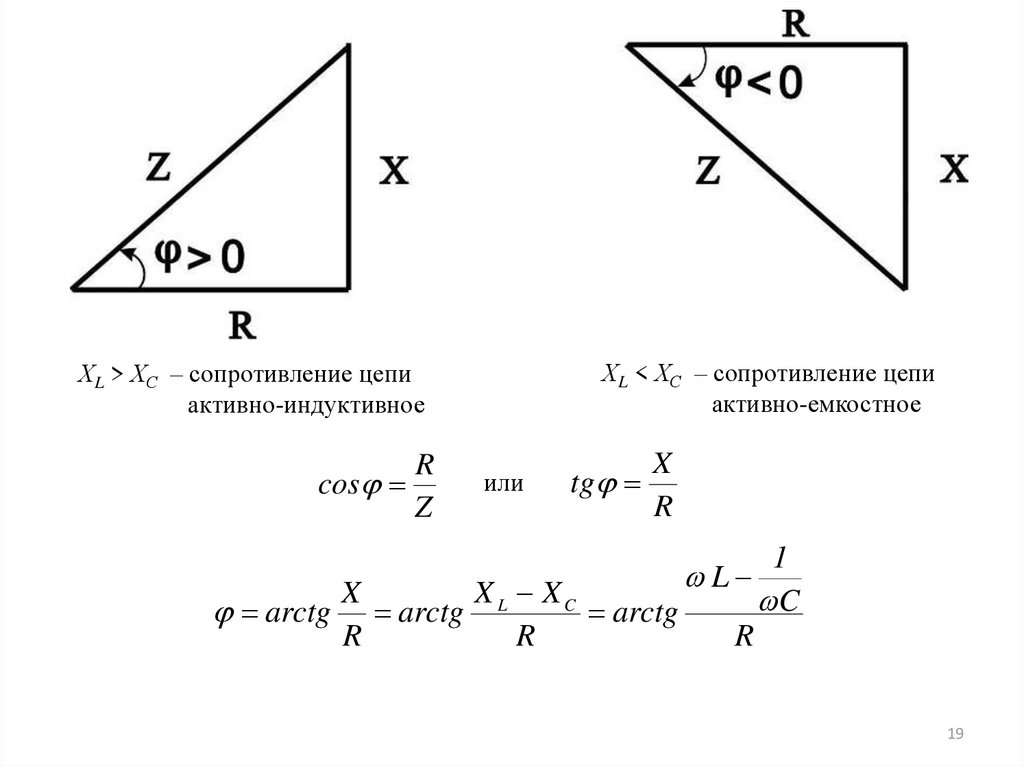
ХL < ХС – сопротивление цепиактивно-емкостное
ХL > ХС – сопротивление цепи
активно-индуктивное
cos
R
Z
или
tg
X
R
1
L
X
X L XC
C
arctg arctg
arctg
R
R
R
19
20.
Закон Ома в комплексной формеU U R U L U C R I jX L I jX C I I ( R j( X L X C ))
U IZ
Комплексное полное сопротивление
U m j
j
Z
e Ze
Im
Модуль полного сопротивления
Um U
Z
Im I
Z R ( X L XC )
2
2
20
21.
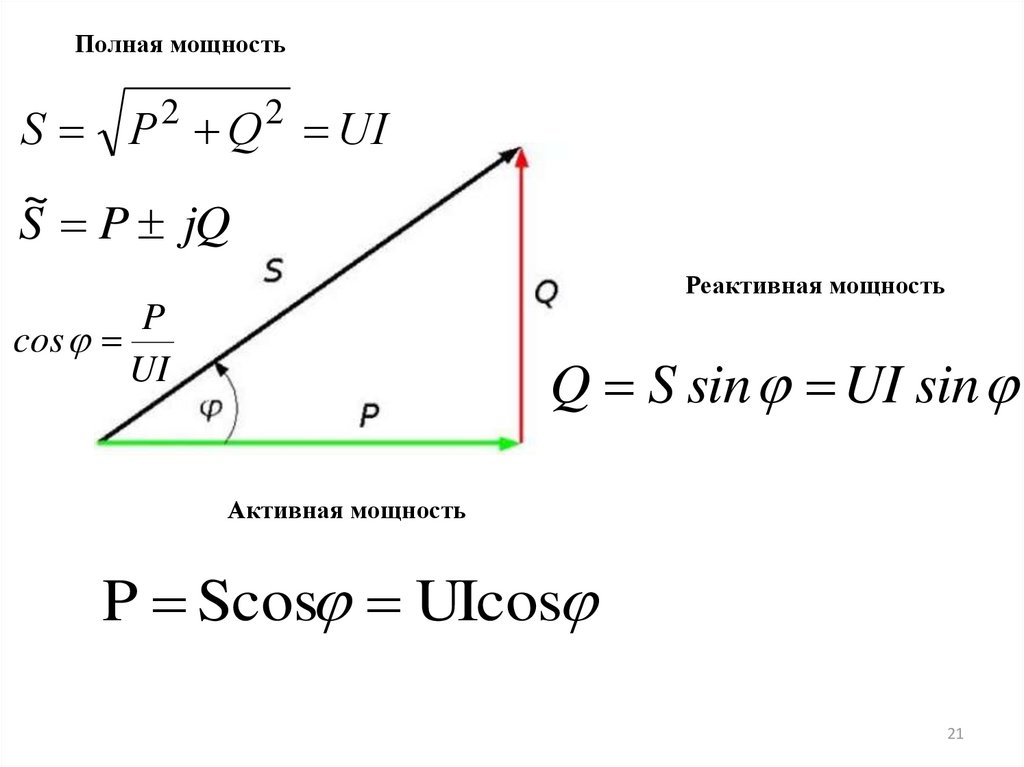
Полная мощностьS P Q UI
2
2
~
S P jQ
Реактивная мощность
P
cos
UI
Q S sin UI sin
Активная мощность
P Scos UIcos
21
22.
Параллельное соединение элементов RLC1
R
U U
U
I I R I L IC
U ( G j( BL BC )) U Y
R jX L jX C
G
BL
1
1
X L L
1
BC
C
XC
Y G jB
I YU
− закон Ома в комплексной форме
Y G jB – если нагрузка активно-индуктивная (ХL > ХС)
Y G jB – если нагрузка активно-емкостная (ХL < ХС)
22
23.
Баланс мощности в цепи синусоидального токаАктивная составляющая: алгебраическая сумма активных мощностей
всех источников энергии равна арифметической сумме мощностей всех
активных элементов
U ист I ист cos( u
Рист
i ) RI R2
РR
Реактивная составляющая: алгебраическая сумма реактивных мощностей
всех источников энергии равна алгебраической сумме реактивных
мощностей всех индуктивных и всех емкостных элементов
U ист I ист sin( u
Qист
i ) X L I L2 X C I C2
QL QC
23
24.
Резонанс в цепях переменного токаR = const
XL = ωL
1
XC =
C
Колебательный контур – электрическая цепь, содержащая катушку индуктивности,
конденсатор и источник электрической энергии. Это простейшая система, в которой
могут происходить электромагнитные колебания
Резонансом называют такой режим в электрической цепи, содержащей катушки
индуктивности и конденсаторы, при котором ее реактивное сопротивление равно
нулю
При резонансе I и U совпадают по фазе
Различают резонанс напряжений и резонанс токов
24
25.
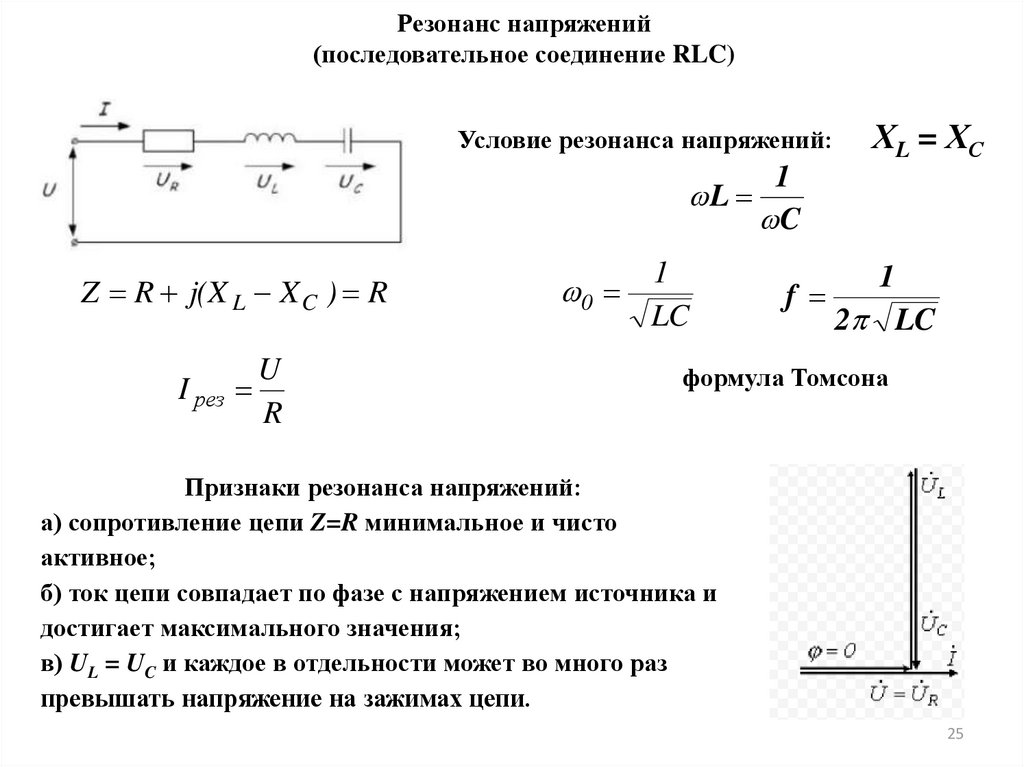
Резонанс напряжений(последовательное соединение RLC)
Условие резонанса напряжений:
ХL = ХС
1
L
C
Z R j(X L X C ) R
I рез
U
R
1
0
LC
f
1
2 LC
формула Томсона
Признаки резонанса напряжений:
а) сопротивление цепи Z=R минимальное и чисто
активное;
б) ток цепи совпадает по фазе с напряжением источника и
достигает максимального значения;
в) UL = UC и каждое в отдельности может во много раз
превышать напряжение на зажимах цепи.
25
26.
ДобротностьДобротность Q – отношение величины электромагнитной энергии, запасенной в
реактивных элементах контура, к энергии, рассеиваемой на активном сопротивлении
контура за один период:
Wзап
Q 2
Wпотр
Добротность показывает, во сколько раз напряжение на индуктивном (емкостном)
элементе превышает входное напряжение в резонансном режиме:
Q
U L U C X L I 0 X L X C 0 L
1
UR UR
RI 0
R
R
R
0CR R
Добротность характеризует «избирательные» свойства резонансного контура, в
частности, его полосу пропускания:
0
Q
Волновое сопротивление
L
C
Q R
26
27.
Резонанс токов(параллельное соединение RLC)
Условие резонанса токов:
I 1 I 1a jI p
ВL = ВС
I 2 I 2 a jI p
I I1a I 2a
0
1
LC
LC
LC
R12
R22
f
1
2 LC
L C R12
L C R22
Признаки резонанса токов:
а) сопротивление Z контура максимальное и чисто
активное;
б) ток в неразветвленной части цепи практически
совпадает по фазе с напряжением источника и
достигает минимального значения;
в) реактивная составляющая тока в катушке равна
реактивной составляющей емкостного тока, причем
эти токи могут во много раз превышать ток источника.
27















 physics
physics electronics
electronics








