Similar presentations:
Цепи синусоидального тока. Лекция 6
1.
1Лекция 6
Цепи синусоидального тока
2.
2Действующие значения синусоидального
напряжения и тока
Математически действующее значение функции
представляет собой ее среднеквадратичное
значение
T
1 2
F
f (t)dt.
T0
(3.33)
3.
Аналогично выражаются и действующиезначения электрических величин
3
T
1 2
U
u (t)dt;
T0
(3.34)
T
1 2
I
i (t)dt ,
T0
где u, i – мгновенные значения напряжения, тока;
T – период функции.
4.
Пусть, например, напряжение представляется ввиде u = Umsin(ωt). Подстановка этой функции в
(3.34) дает:
4
1T 2
Um
2
U
(U m sin t)dt
T0
2
Действующее значение меньше амплитудного в
2
раз.
Um
Im
U
; I
;
2
2
Em
E
.
2
(3.35)
5.
5На щитках электрических машин и аппаратов
переменного тока в качестве номинальных
указываются действующие значения
напряжений и токов.
Измерительные приборы измеряют
действующие значения соответствующих
величин.
6.
Комплексные действующие значения иликомплексы напряжений и токов:
6
7.
7Мгновенная мощность
p=ui
u U m sin t,
(3.36)
i Im sin( t ),
p ui U m sin t I m sin( t )
U m I m sin t sin( t ).
8.
81
p U m I m cos cos(2 t )
2
UI cos cos(2 t ) .
(3.37)
Мгновенная мощность является периодической
функцией, изменяющейся с двойной частотой по
отношению к частоте напряжения и тока.
9.
Мгновенная мощность для сопротивления r неимеет отрицательных значений.
p
u
i
p=ui
UI
t
i
u
9
10.
10p
u
i
u
p=ui
+
–
+
i
–
+
t
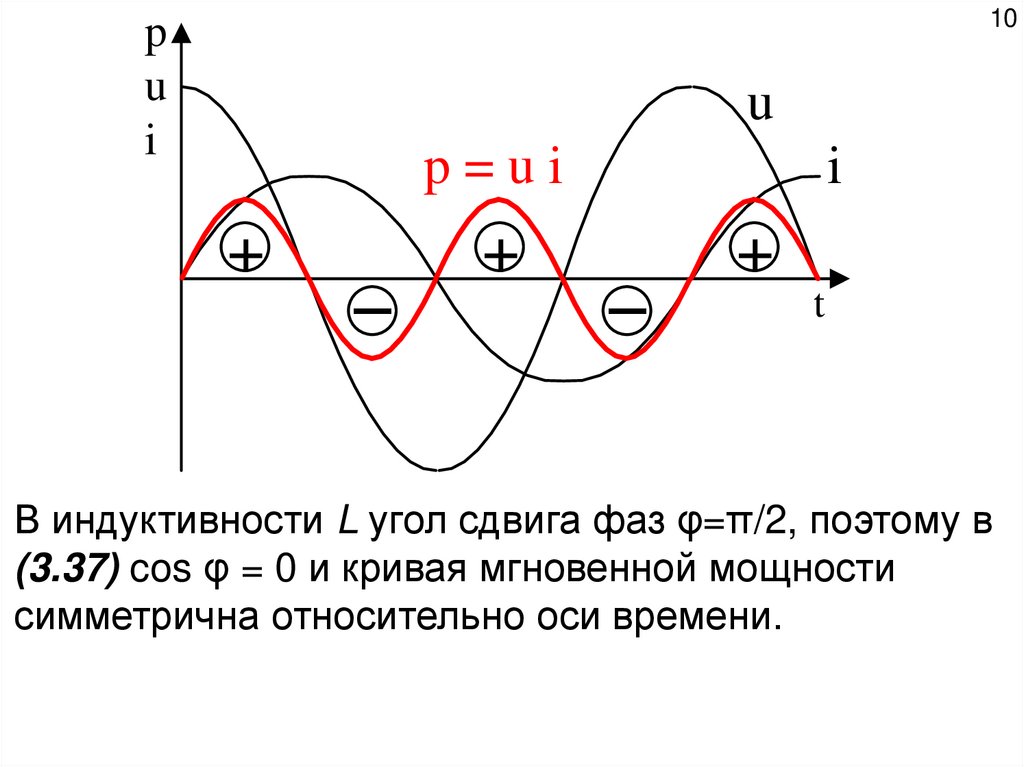
В индуктивности L угол сдвига фаз φ=π/2, поэтому в
(3.37) cos φ = 0 и кривая мгновенной мощности
симметрична относительно оси времени.
11.
11Это значит, что в части периода энергия
поступает от источника в индуктивность, в
другой – возвращается источнику.
12.
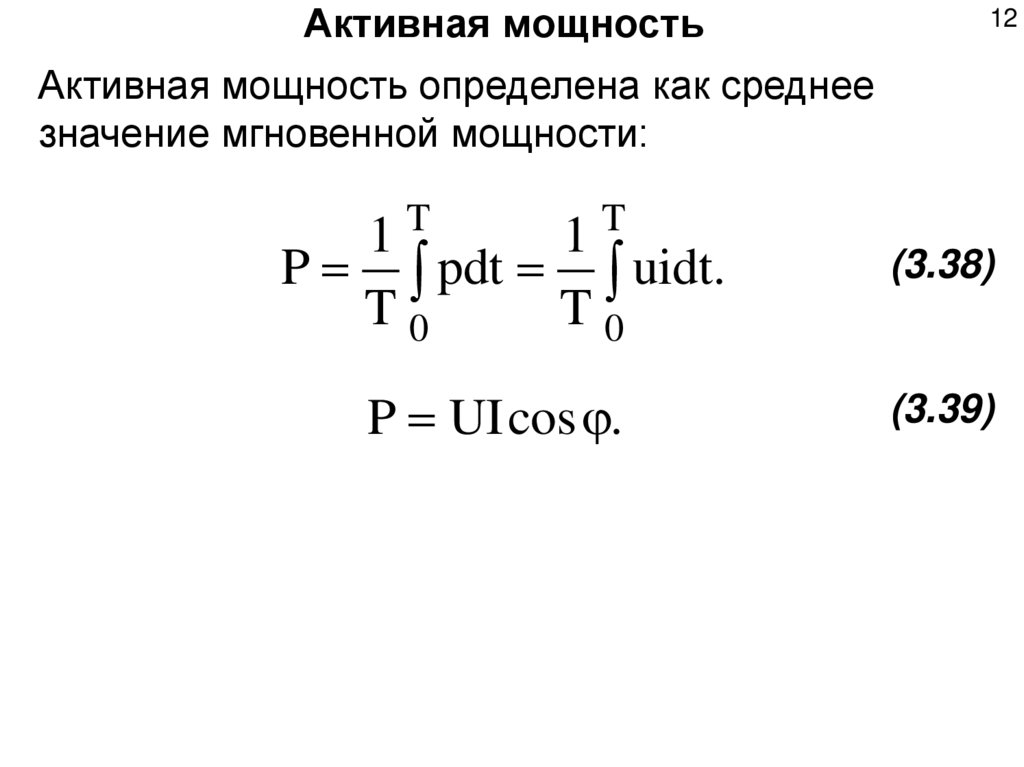
Активная мощность12
Активная мощность определена как среднее
значение мгновенной мощности:
T
T
1
1
P pdt uidt.
T0
T0
(3.38)
P UIcos .
(3.39)
13.
13Произведение
UI S
есть полная мощность, поэтому активная
мощность записывается также в виде:
P Scos
(3.40)
Единица измерения активной мощности –
ватт (Вт); полная мощность измеряется в вольтамперах (ВА).
14.
14Реактивная мощность определяется формулой
Q UIsin .
Единица измерения Q – вольт-ампер реактивный
(вар).
15.
15Мощность в комплексной форме или
комплексная мощность
Комплексная мощность представляет собой
произведение комплекса напряжения на
сопряженный комплекс тока:
S U I.
(3.41)
16.
16I Ie
Пусть
j
.
Осуществим подстановку этих значений в (3.41):
j
S U I Ue Ie
UIe
j
P jQ
j
UIe
j( )
UIcos jUIsin
Q
jarctg
2
2
P
P Q e
Se
j
17.
17Коэффициент мощности –
это отношение активной мощности к
полной:
P P
cos
.
UI S
18.
Баланс мощностейSист Sпотр ;
Pист jQист Pпотр jQпотр ;
Pист Pпотр ;
Q
Q
.
ист
потр
18
19.
Мощности Pист и Qист определяются через входноенапряжение и входной ток:
Pист U вх Iвх cos вх ;
Qист U вх Iвх sin вх .
С использованием выражения для комплексной
мощности получим:
S U вх Iвх U вх Iвх cos вх jU вх Iвх sin вх .
19
20.
Составляющие Pпотр и Qпотр удобно записыватьпоэлементно:
Pпотр I k2 rk ;
k
2
Qпотр I k x k .
k
При этом следует учитывать, что все
составляющие активной мощности Pпотр
положительны. Слагаемые Qпотр имеют разные
знаки:
– индуктивные составляющие I2kxLk имеют знак
«плюс»;
– емкостные составляющие I2kxCk – «минус».
20
21. Комплексные соотношения для трехэлементных электрических цепей
22.
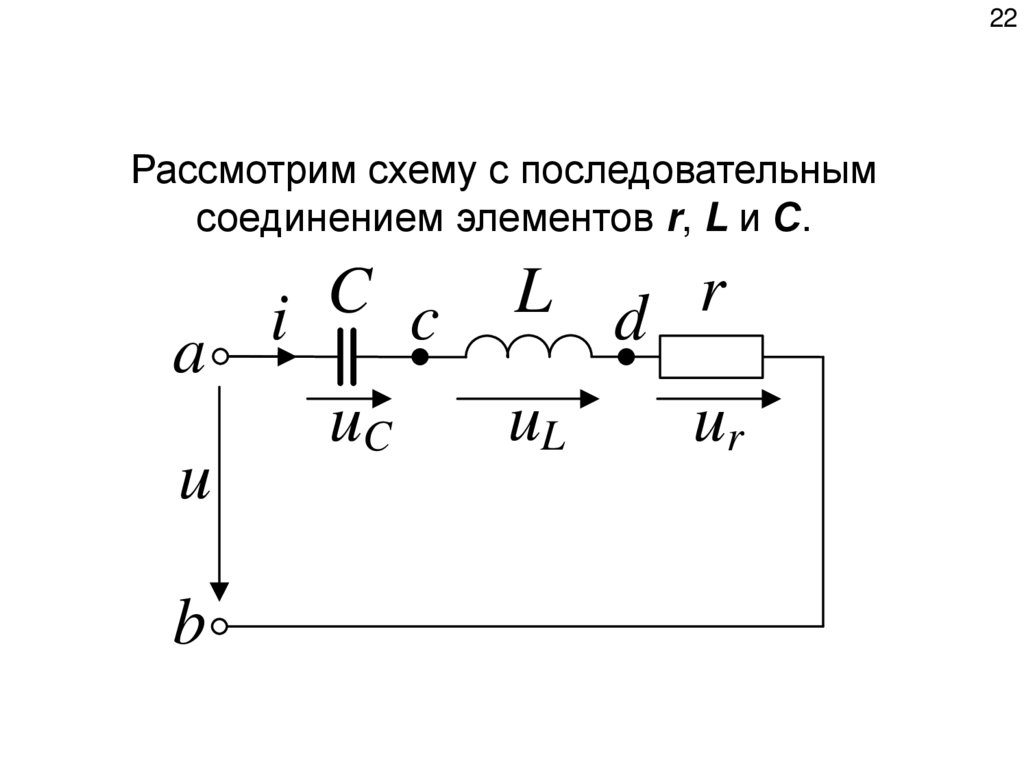
22Рассмотрим схему с последовательным
соединением элементов r, L и С.
C
i
c
a
uC
u
b
L d r
uL
ur
23.
23Записываем уравнение для мгновенных
значений по второму закону Кирхгофа:
ur uL uC u
или
di 1
ri L idt u.
dt C
(3.42)
24.
Пусть24
u U m sin( t );
i I sin( t )
m
Условимся использовать запись по комплексным
действующим значениям, которые в данном случае
имеют вид:
тогда уравнению (3.42) в комплексной форме будет
соответствовать уравнение:
(3.43)
25.
11
j
С учетом
уравнение (3.43)
j C
C
преобразуется в следующей последовательности:
25
26.
гдеx xL xC
Z r jx
– реактивное сопротивление;
x
jarctg
2
2
j
r
r x e
ze
комплексное сопротивление цепи;
z r
2
2 – полное сопротивление или
x
модуль комплексного сопротивления;
x
arctg
r
– аргумент комплексного
сопротивления, представляющий собой угол
сдвига фаз между входным напряжением и
током.
26
27.
Установленные здесь закономерности имеютобщий характер и сводятся к следующему:
1. Индуктивное и емкостное сопротивления в
состав общего реактивного сопротивления
входят с разными знаками (индуктивное – с
плюсом, емкостное – с минусом).
2. Модуль комплексного сопротивления есть
полное сопротивление.
3. Аргументом комплексного сопротивления
всегда является угол сдвига фаз между
соответствующими напряжением и током.
27
28.
28Результатом решения (3.43) является
комплексное действующее значение тока
(комплекс тока), по которому легко
записывается мгновенное значение:
U
I i I 2 sin( t ).
Z
29.
29+j
Для построения
векторной диаграммы
выбирают масштабы
действующих значений
тока и напряжений
(модулей комплексов).
+1
30.
30+j
·
I
α
+1
Общей величиной для
всех элементов является
ток I. Поэтому вектор
тока на данной
диаграмме является
исходным или базовым.
31.
31+j
·
I
α
+1
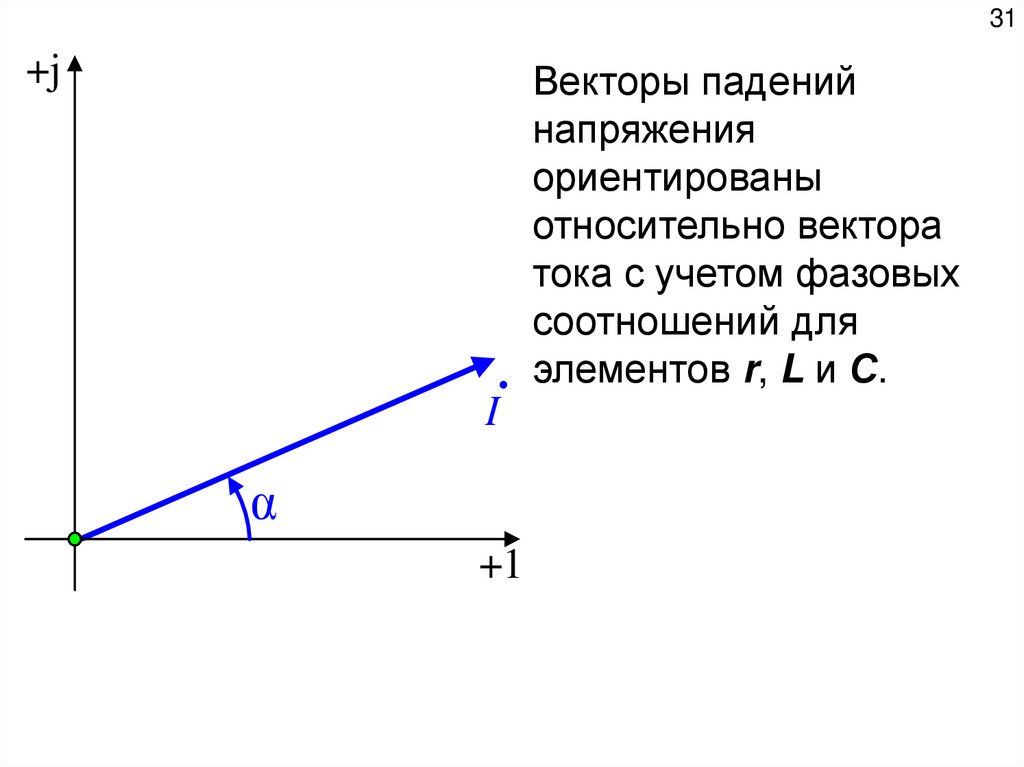
Векторы падений
напряжения
ориентированы
относительно вектора
тока с учетом фазовых
соотношений для
элементов r, L и С.
32.
32+j
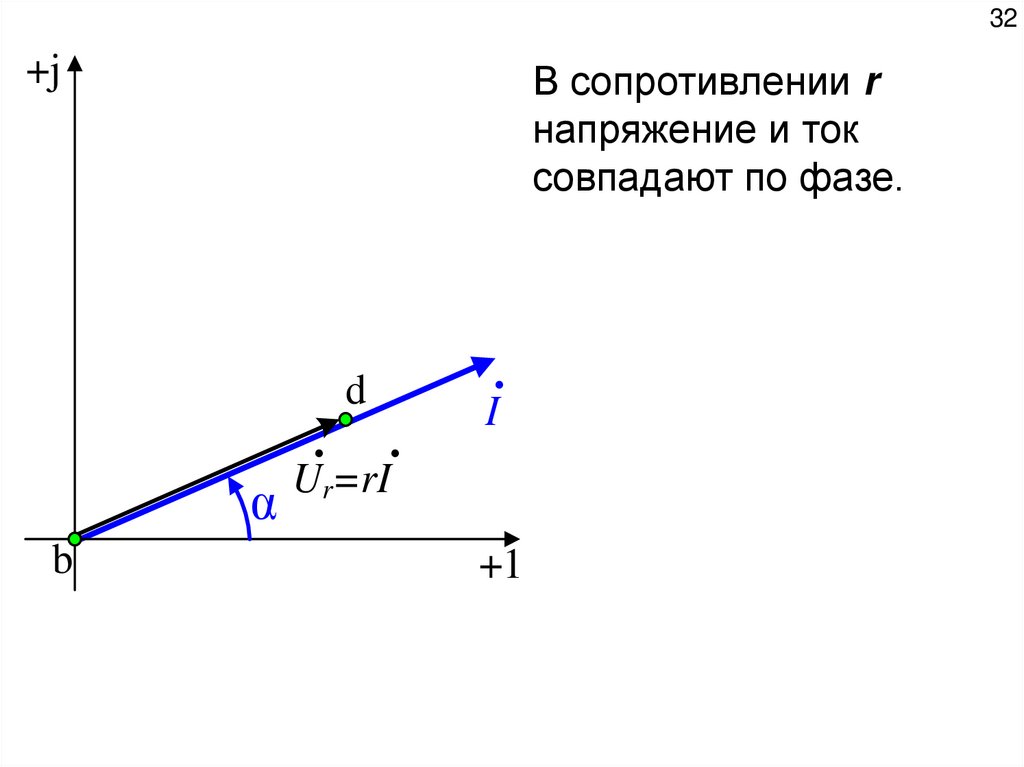
В сопротивлении r
напряжение и ток
совпадают по фазе.
d
α
b
· ·
·
I
Ur=rI
+1
33.
33+j
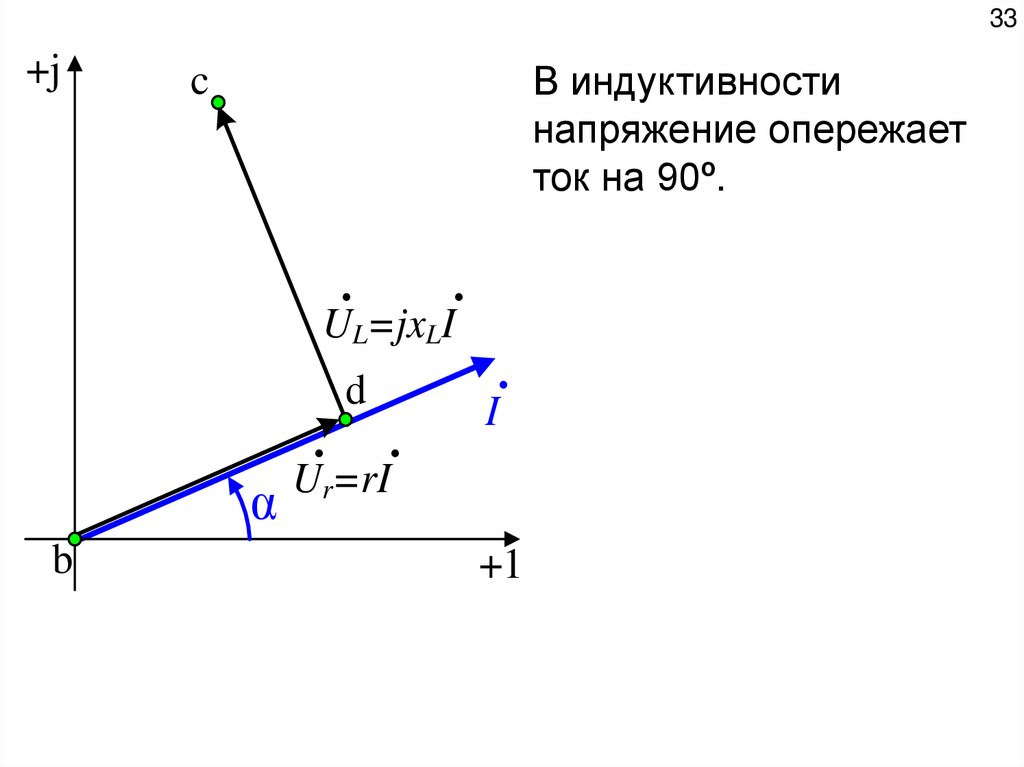
В индуктивности
напряжение опережает
ток на 90º.
c
· ·
UL=jxLI
d
α
b
· ·
·
I
Ur=rI
+1
34.
34+j
В емкости напряжение
отстает от тока на 90º.
c
·
·
UC=–jxCI
· ·
a
UL=jxLI
d
α
b
· ·
·
I
Ur=rI
+1
35.
+j35
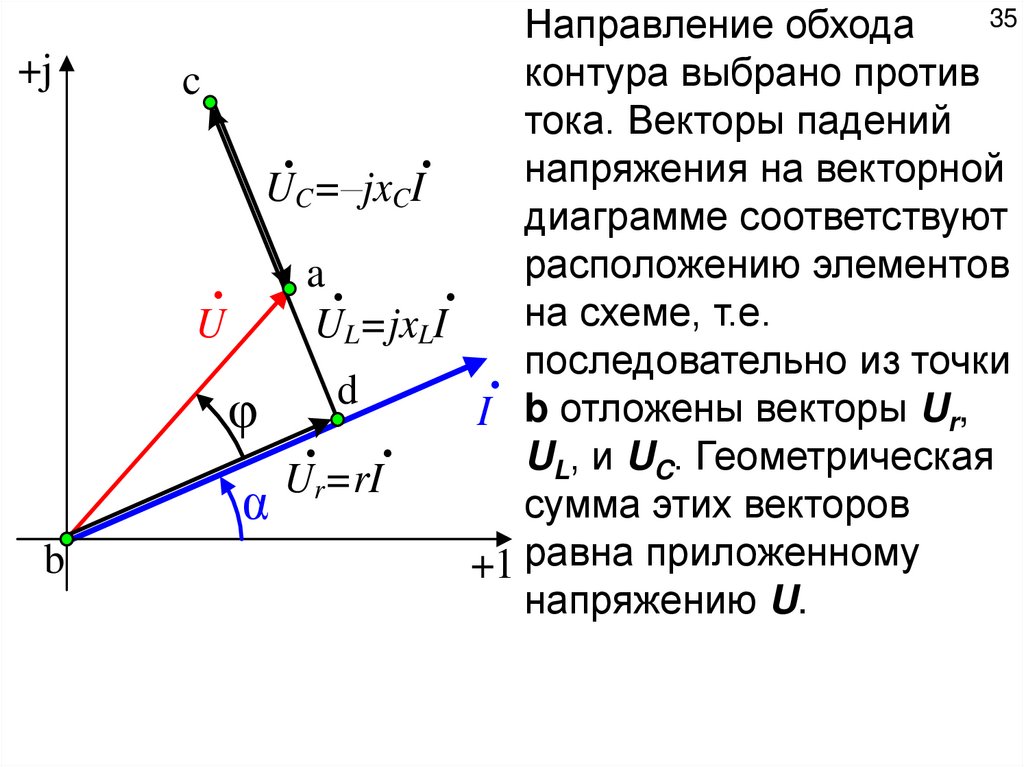
Направление обхода
контура выбрано против
c
тока. Векторы падений
напряжения на векторной
UC=–jxCI
диаграмме соответствуют
расположению элементов
a
на схеме, т.е.
U
UL=jxLI
последовательно из точки
d
I b отложены векторы Ur,
φ
UL, и UC. Геометрическая
Ur=rI
сумма этих векторов
α
+1 равна приложенному
напряжению U.
·
·
·
· ·
· ·
b
·
36.
36Векторные диаграммы такого типа
называются топографическими
векторными диаграммами.
Главная их особенность – соответствие
расположения векторов падений напряжений
расположению элементов на схеме.
37.
37Построенная векторная диаграмма соответствует
случаю, когда индуктивное сопротивление xL,
равное ωL, превышает емкостное xC, равное
1/(ωС), поэтому падение напряжения на
индуктивности UL=xLI, больше падения
напряжения UC=xCI, угол φ положителен,
напряжение по фазе опережает ток и
относительно входных зажимов схема
воспринимается как активно-индуктивная.













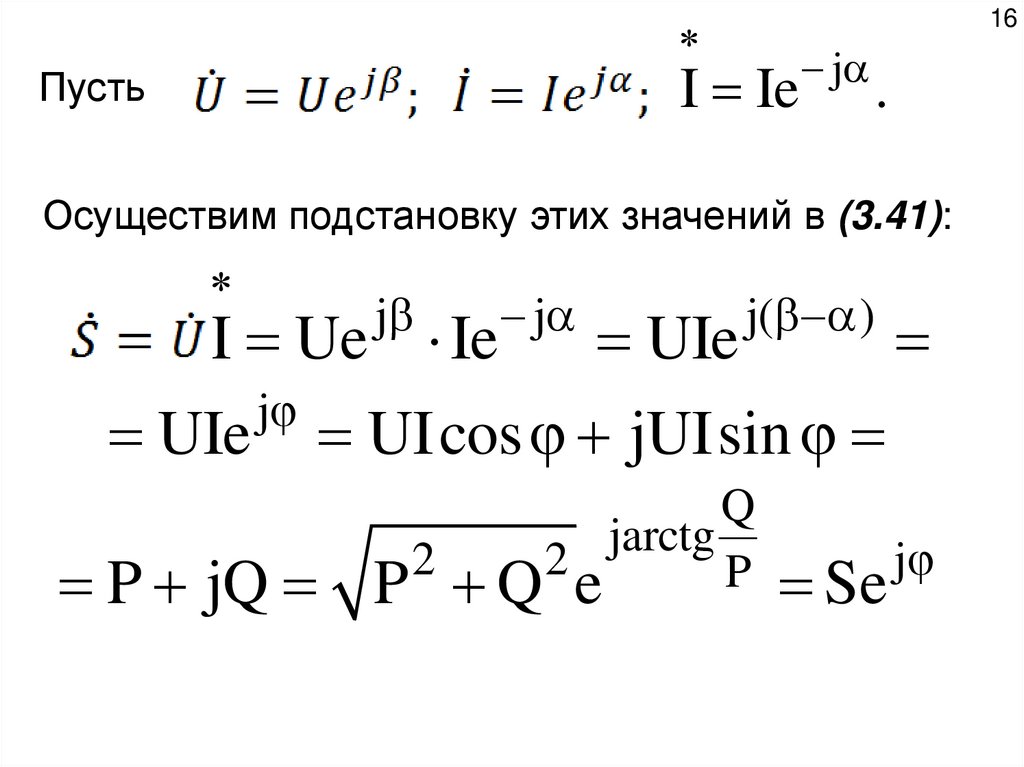















 physics
physics








