Similar presentations:
Гармонические колебания и их параметры
1.
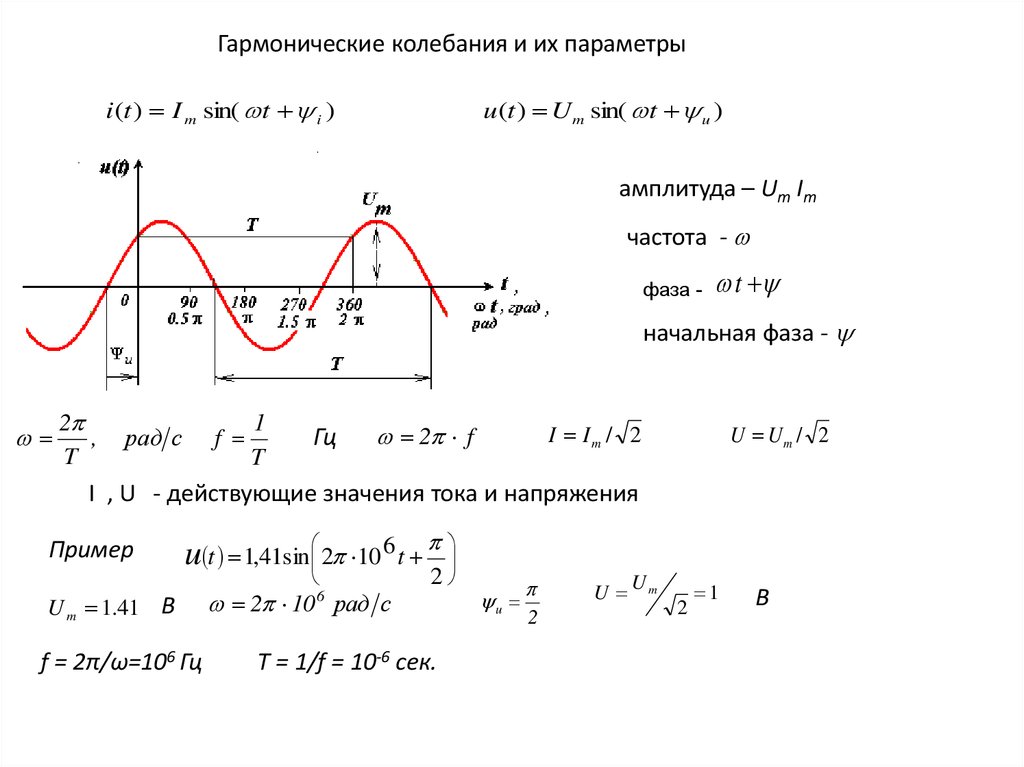
Гармонические колебания и их параметрыi(t ) I m sin( t i )
u (t ) U m sin( t u )
амплитуда – Um Im
частота -
фаза -
t
начальная фаза -
2
,
T
f
рад с
1
T
Гц
2 f
U Um / 2
I Im / 2
I , U - действующие значения тока и напряжения
Пример
u t 1,41sin 2 10 6 t
U m 1.41 B
f = 2π/ω=106 Гц
2 10 рад с
2
6
Т = 1/f = 10-6 сек.
u
2
U
Um
2
1
B
2.
Представление гармонических колебаний комплексными числамиu (t ) U m sin( t u ) Im(U m e j ( t u ) ) Im(U m cos( t u ) jU m sin( t u ))
комплексная амплитуда напряжения
U m U me
комплексная амплитуда тока
j u
I m I m e j i
U m sin( t u ) U m e j u
Комплекс действующего значения напряжения и тока
U Ue
j u
I Ie j i
изображение на комплексной плоскости по координатам в полярной
системе координат
3.
Комплексы в декартовой системе координатU a jb
a U cos u b U sin u
U a b
2
2
b
a
u arctg
4.
Идеализированные пассивные элементыR
L
C
в режиме воздействия на них гармонического колебания
электрическое сопротивление
R
i(t ) I m sin( t i )
I Ie j i
u(t ) i(t ) R I m R sin( t i )
U R I
U R I
u i 0
u i
Комплексное сопротивление для электрического сопротивления
U
Zr R
I
Комплексная проводимость
Yr
1
1
G
Zr R
R
5.
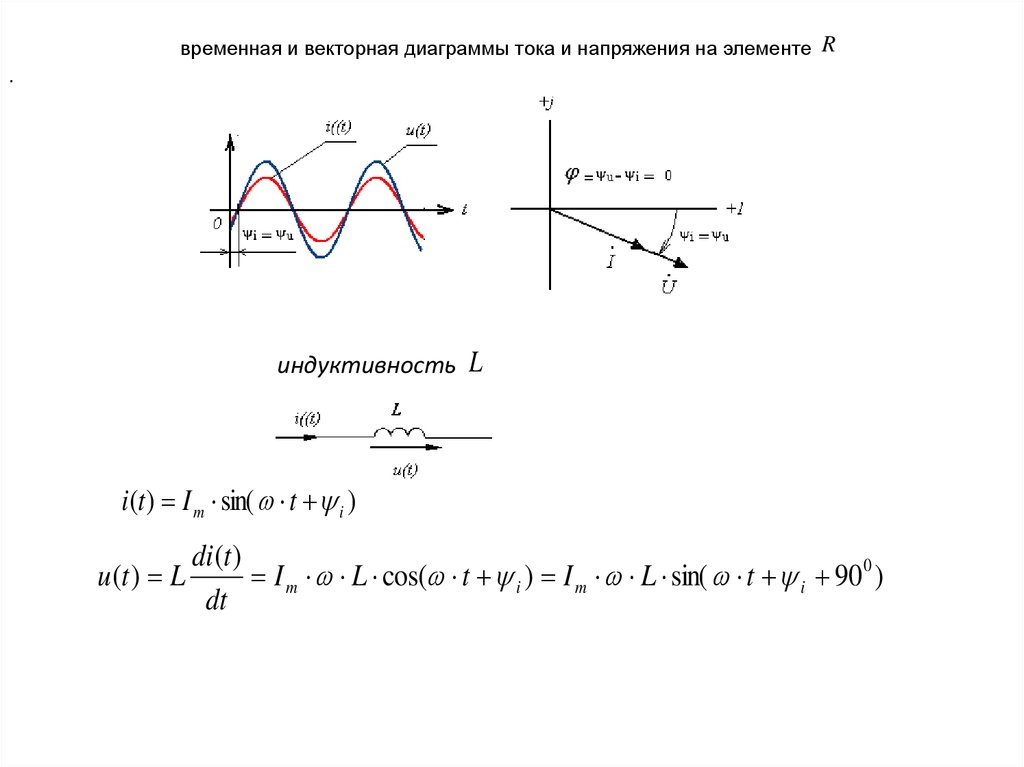
временная и векторная диаграммы тока и напряжения на элементе R.
индуктивность L
i(t ) I m sin( t i )
u (t ) L
di(t )
I m L cos( t i ) I m L sin( t i 900 )
dt
6.
j ( 1 900 )U m I m Le
j LI m
j ( 1 900 )
U I Le
j LI
X L L
индуктивное сопротивление синусоидальному току
Z L jX L
комплексное сопротивление индуктивности
1
YL
j bL
ZL
1
1
bL
X L L
комплексная проводимость индуктивности
проводимость индуктивности
u i 90 0
7.
частотная характеристика индуктивного элементавременная и векторная диаграммы тока и напряжения на индуктивности
8.
емкостьC
i(t ) I m sin( t i )
1
1
1
u (t ) i (t )dt
I m ( cos( t i ))
I m sin( t i 90 0 )
C
C
C
1
1
1
j ( i 900 )
U
I e
j
I e j i I
C
C
j C
1
XС
C
Z С jX C
емкостное сопротивление синусоидальному току
комплексное сопротивление емкости
9.
YС1
j bC комплексная проводимость для емкостного элемента
ZС
bC
1
C
XC
проводимость емкости
u i 90 0
частотная характеристика емкостного элемента
10.
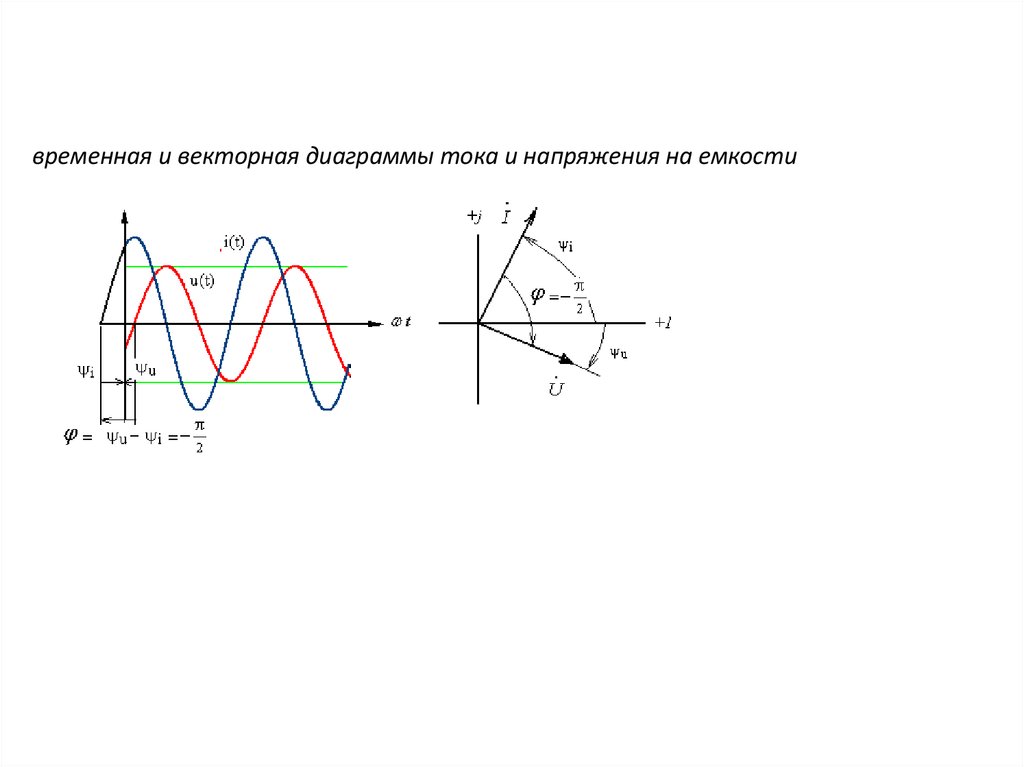
временная и векторная диаграммы тока и напряжения на емкости11.
первый закон Кирхгофа в комплексной формеn
I
k 1
k
0
второй закон Кирхгофа в комплексной форме
n
U
k 1
k
0
закон Ома в комплексной форме
U I Z
12.
расчет простейших электрических цепей в режиме гармоническихколебаний
дано
R
L
e(t ) Em sin( t e )
решение
E E e j e
Zr R
I E
Z0
Z0 Zr ZL
Z L j XL
XL L
U r I Z r
комплексная схема замещения
U L I Z L
13.
расчет ЭЦ при числовых значенияхEm 100 2
E
В
Em
100
2
R
100 Ом
L
0.318 Гн
f 50 Гц
j150
E 100e
2 f 2 50 314
X L L 314 0.318 100
Z L j X L j100
частота
Ом
Ом
j 150
E
100
e
j 300
I
1 e
R Z L 100 j100
j 300
j 600
U L I Z L 1 e
j100 100 e
j 300
j 300
U r I R 1 e
100 100 e
e 15 0
14.
переход от комплексов к синусоидальным функциямi (t ) 1 2 sin( t 300 )
u L (t ) 100 2 sin( t 60 )
0
ur (t ) 100 2 sin( t 300 )
векторная диаграмма тока и напряжений












 physics
physics








