Расчет гармонических колебаний в электрических цепях

1.

Федеральное государственное казенное военное
образовательное учреждение высшего профессионального образования
«Военная академия связи имени Маршала Советского Союза С.М. Буденного»
Министерства обороны Российской Федерации
2 кафедра
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
по учебной дисциплине«Электроника, электротехника и схемотехника»
(Д-0201-2)
Раздел № 1
Электротехника
Тема № 2
Режим гармонических колебаний
в линейных электрических цепях
Занятие №8
Расчет гармонических колебаний
в электрических цепях
Санкт-Петербург

2.

УЧЕБНЫЕ ВОПРОСЫ:
1. Анализ гармонических колебаний в простейших
электрических цепях
2. Анализ гармонических колебаний в сложных
электрических цепях
3. Контроль усвоения изученного материала
ЛИТЕРАТУРА:
1) Улахович Д.А.Основы теории линейных электрических цепей:
Учебное пособие. - СПб.: БХВ-Петербург, 2009.
2) Бабкова Л.А., Киселев О.Н. Методические рекомендации к
практическим занятиям и руководство к лабораторным
работам по дисциплине «Основы теории цепей»: Учеб.
пособие.– СПб.: ВАС, 2011, стр.19-27.

3.

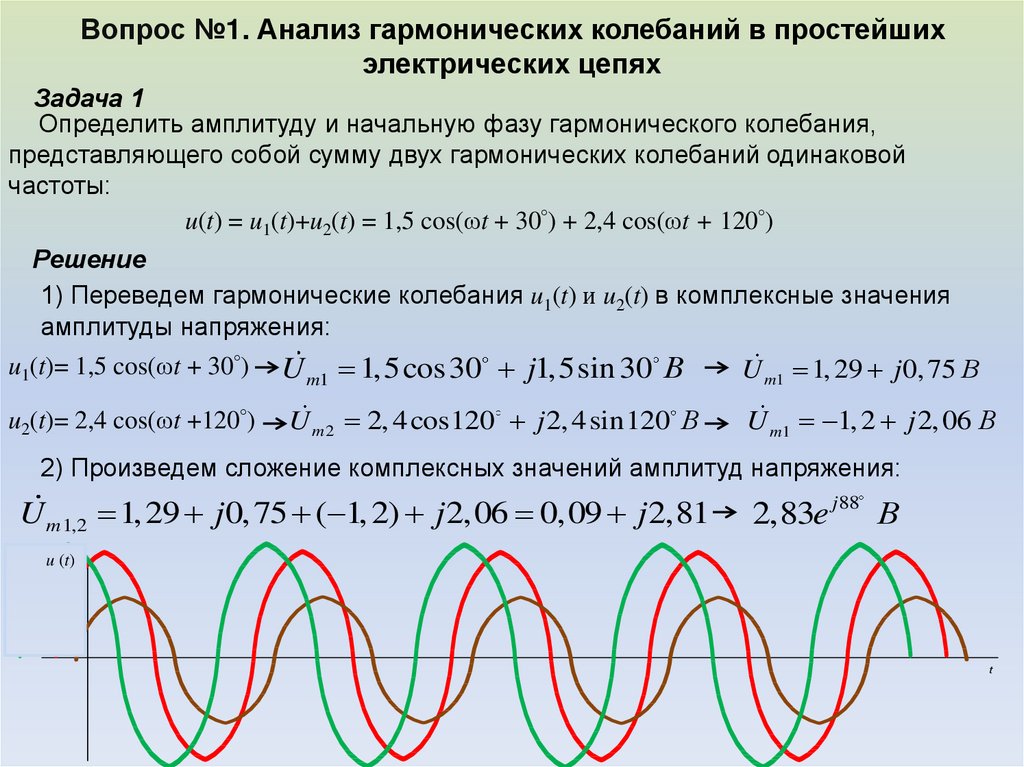
Вопрос №1. Анализ гармонических колебаний в простейших
электрических цепях
Задача 1
Определить амплитуду и начальную фазу гармонического колебания,
представляющего собой сумму двух гармонических колебаний одинаковой
частоты:
u(t) = u1(t)+u2(t) = 1,5 cos(ωt + 30°) + 2,4 cos(ωt + 120°)
Решение
1) Переведем гармонические колебания u1(t) и u2(t) в комплексные значения
амплитуды напряжения:
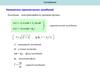
u1(t)= 1,5 cos(ωt + 30°)
U m1 1,5cos 30 j1,5sin 30 В
U m1 1, 29 j 0, 75 В
u2(t)= 2,4 cos(ωt +120°)
U m 2 2, 4 cos120 j 2, 4sin120 В
U m1 1, 2 j 2, 06 В
2) Произведем сложение комплексных значений амплитуд напряжения:
Um 1,2 1, 29 j 0,75 ( 1, 2) j 2,06 0,09 j 2,81
2,83e j 88 В
u (t)
u(t)
t

4.

.
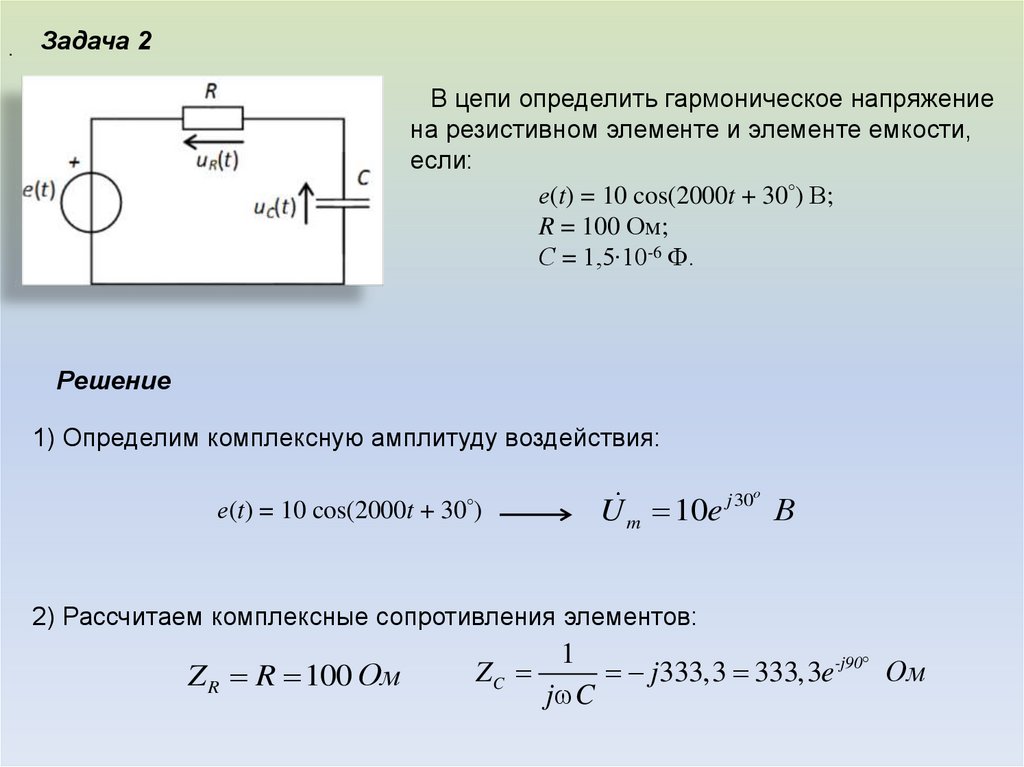
Задача 2
В цепи определить гармоническое напряжение
на резистивном элементе и элементе емкости,
если:
е(t) = 10 cos(2000t + 30°) В;
R = 100 Ом;
С = 1,5∙10-6 Ф.
Решение
1) Определим комплексную амплитуду воздействия:
е(t) = 10 cos(2000t +
30°)
U m 10e
j 30o
В
2) Рассчитаем комплексные сопротивления элементов:
Z R R 100 Ом
ZC
1
j 333,3 333,3e-j90 Ом
j C

5.

3. Схема замещения цепи будет выглядеть следующим образом:
4) Произведем расчет комплексных амплитуд
реакции.
3.1) Определим эквивалентное комплексное
сопротивление:
Z RC
1
Z R ZC R
100 j 333,3 Ом
j C
Переведем в показательную форму:
Z RC 100 j 333,3 348е j 73,3 Ом
3.2) Определим комплексное амплитудное значение тока (первую реакцию).
Применим закон Ома в комплексной форме:
Um
10e j 30
j103,3
Im
0,
02873
е
А
j 73,3
Z RC 348е
3.3) Определим комплексное амплитудное значение напряжения на элементе
сопротивления (вторую реакцию).
U mR I m Z R 0, 02873е j103,3 100 2,873е j103,3 В

6.

3.4) Определим комплексное амплитудное значение напряжения на элементе
емкости (третью реакцию).
U mC I m Z C 0, 02873е j103,3 333,3e-j90 9,578e j13,3 В
Проведем проверку полученных результатов по второму закону Кирхгофа в
комплексной форме:
U m U mR U mС 0 U m U mR U mС
10e j 30 2,873е j103,3 9,578e j13,3
o
10 cos 30 j10sin 30 2,873cos(103,3) j 2,873sin(103,3) 9,578cos13,3 j 9,578sin13,3
4) Запишем мгновенные значения полученных реакций:
i(t) = 0,02873 cos(2000t +103,3°) А
uR(t) = 2,873 cos(2000t + 103,3°) В
u(t)
i (t)
t
uС(t) = 9,578 cos(2000t + 13,3°) В
5) Вывод: а) анализируя мгновенное значение напряжения на элементе
сопротивления можно видеть, что данный элемент частотно
независимый, и начальная фаза совпадает с начальной фазой тока;
б) анализируя мгновенное значение напряжения на элементе емкости
можно видеть, что начальная фаза отстает от начальной фазы тока
на 90°.

7.

Вопрос №2. Анализ гармонических колебаний в сложных
электрических цепях
Задача 3
Для электрической цепи определить мгновенное
значение iL(t), если известно:
u(t) = 4 cos(106t - 40°) В;
R = 1 Ом;
С = 0,5∙10-6 Ф;
L= 10-6 Г.
Решение
1) Определим комплексную амплитуду воздействия:
u(t) = 4
cos(106t
-
40°)
U m 4e
j 40o
2) Рассчитаем комплексные сопротивления элементов:
Z R R 1 Ом
1
ZC
j2 2e-j90 Ом
j C
Z L j L j e
j90
Ом
B

8.

Схема замещения цепи будет выглядеть следующим образом:
3) Произведем расчет комплексных амплитуд
реакции.
3.1) Определим эквивалентное комплексное
сопротивление:
Z RL
ZRZL
1j
j (1 j )
1 j
1 j Ом
Z R Z L 1 j (1 j ) (1 j )
1
ZCRL ZC Z RL 1 j j 2 1 j Ом
Переведем в показательную форму:
ZCRL 1 j 1, 41e j 45
3.2) Определим комплексное амплитудное значение тока.
Применим закон Ома в комплексной форме:
j 40o
Um
4e
j 5o
Im
2,83е А
j 45
Z RCL 1, 41е
3.3) Определим комплексное амплитудное значение напряжения на элементе
емкости.
U mC I m Z C 2,83е
j 5o
2e
j 90
5, 66е
j 85o
B

9.

Применим второй закон Кирхгофа в комплексной форме:
U m U mRL U mС 0 U mRL U m U mС
U mRL 4е
j 40o
5, 66e
j 85o
(3, 06 j 2,57) (0,5 j5, 64) 2,56 j3, 07 4e j 50 B
Т.к. элемент сопротивления и элемент емкости соединены параллельно, то
U mRL U mR U mL
3.4) Определим комплексное амплитудное значение тока на элементе
индуктивности.
o
I mL
U mRL 4е j 50
j 40o
j 90o 4e
А
ZL
e
4) Запишем мгновенное значение полученной реакции:
iL(t) = 4 cos(106t -40°) A
5) Вывод: анализируя мгновенное значение тока на элементе индуктивности
можно видеть, что колебания тока и напряжения одинаковы, а
начальная фаза тока отстает от начальной фазы напряжения на
90°.