Similar presentations:
Расчет комплексных сопротивлений электрических цепей
1.
Федеральное государственное казенное военноеобразовательное учреждение высшего профессионального образования
«Военная академия связи имени Маршала Советского Союза С.М. Буденного»
Министерства обороны Российской Федерации
2 кафедра
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
по учебной дисциплине«Электроника, электротехника и схемотехника»
(Д-0201-2)
Раздел № 1
Электротехника
Тема № 2
Режим гармонических колебаний
в линейных электрических цепях
Занятие №7 Расчет комплексных сопротивлений
электрических цепей
Санкт-Петербург
2.
УЧЕБНЫЕ ВОПРОСЫ:1. Расчет комплексных сопротивлений параллельнопоследовательных электрических цепей
2. Контроль усвоения изученного материала
ЛИТЕРАТУРА:
1. Бабкова Л.А., Бирюков А.А., Дьяков С.В., Киселев О.Н. Теория электрических цепей.
Анализ электрических цепей: Учебн. Пособие.-СПб.:ВАС, 2015.- 256 с.: ил. Стр. 78-97.
2. Улахович Д. А. Основы теории линейных электрических цепей: Учебное пособие. - СПб.:
БХВ-Петербург, 2009. Стр.103-119.
3. Бабкова Л. А., Киселёв О. Н. Методические рекомендации к
практическим занятиям и руководство к лабораторным работам по
дисциплине «Основы теории цепей»: Учеб. пособие. – СПб.: ВАС,
2011. – 116. стр.17-19.
3.
.Вопрос №1. Расчет комплексных сопротивлений
двухполюсников
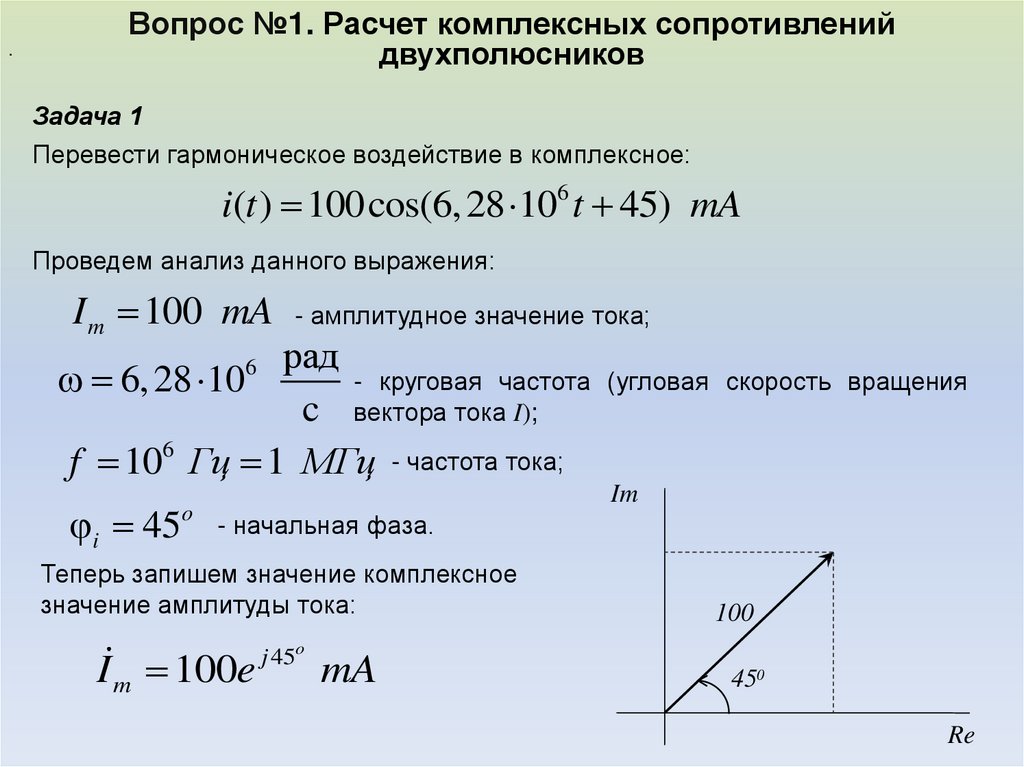
Задача 1
Перевести гармоническое воздействие в комплексное:
i(t ) 100cos(6, 28 106 t 45) mA
Проведем анализ данного выражения:
I m 100 mA
- амплитудное значение тока;
рад
- круговая частота
6, 28 10
c вектора тока I);
f 106 Гц 1 МГц - частота тока;
6
i 45
o
(угловая скорость вращения
Im
- начальная фаза.
Теперь запишем значение комплексное
значение амплитуды тока:
I m 100e
j 45o
mA
100
450
Re
4.
Перейдем к комплексному действующему значению тока:100 j 45o
j 45o
I
e
70,9е
mA
2
Задача 2 (самостоятельно)
Перевести гармоническое воздействие в комплексное:
u(t ) 220cos(6.28 103 t 30) В
Решение:
U m 220 В
- амплитудное значение напряжения;
рад
- круговая частота (угловая
6.28 10
c вектора тока U);
f 103 Гц 1 кГц - частота напряжения;
3
u 30
o
- начальная фаза.
скорость вращения
Im
Комплексное значение амплитуды
напряжения:
U m 220e
j 30o
В
220
300
Re
5.
Задача 3Записать мгновенные значения гармонических колебаний, если f = 105 Гц, а
соответствующие комплексные амплитуды равны:
I m 3, 7 10 3 e j125
I m 0,5e j15
Um 3 j
i(t ) 3,7 10 3 cos(6.28 105 t 125) mA
i(t ) 0,5cos(6.28 105 t 15) mA
u(t ) 3, 2cos(6.28 105 t 18,3) В
Задача 4
Определить активное, реактивное, полное сопротивления и активную,
реактивную, полную проводимость следующих двухполюсников:
R
L
т.к. Z R ( j r + jx, то Z R ( j R+ j0 Z R ( j R
1
т.к. YR ( j g + jb, то YR ( j + j0 YR ( j G
R
т.к. Z L ( j r + jx, то Z L ( j 0+ j L Z L ( j j L
1
1
т.к. YL ( j g + jb, то YL ( j 0+
YL ( j
j L
j L
6.
С1
1
т.к. ZC ( j r + jx, то ZC ( j 0+
ZC ( j
j C
j C
т.к. YC ( j g + jb, то YC ( j 0+ j C YC ( j j C
Задача 4
Для двухполюсника, схема которого изображена на
рисунке, определить Z(jω), r, x, Y(jω), g, b, если:
R = 20 кОм;
1) f = 3 кГц, 2) f = 3 МГц, 3) f = 3 ГГц.
R
Задача 5
Для двухполюсника, схема которого изображена на
рисунке, определить Z(jω), r, x, Y(jω), g, b, если:
L = 40 мкГ;
1) f = 3 кГц, 2) f = 3 МГц, 3) f = 3 ГГц.
L
Задача 6
С
Для двухполюсника, схема которого изображена на
рисунке, определить Z(jω), r, x, Y(jω), g, b, если:
С = 60 мФ;
1) f = 3 кГц, 2) f = 3 МГц, 3) f = 3 ГГц.
7.
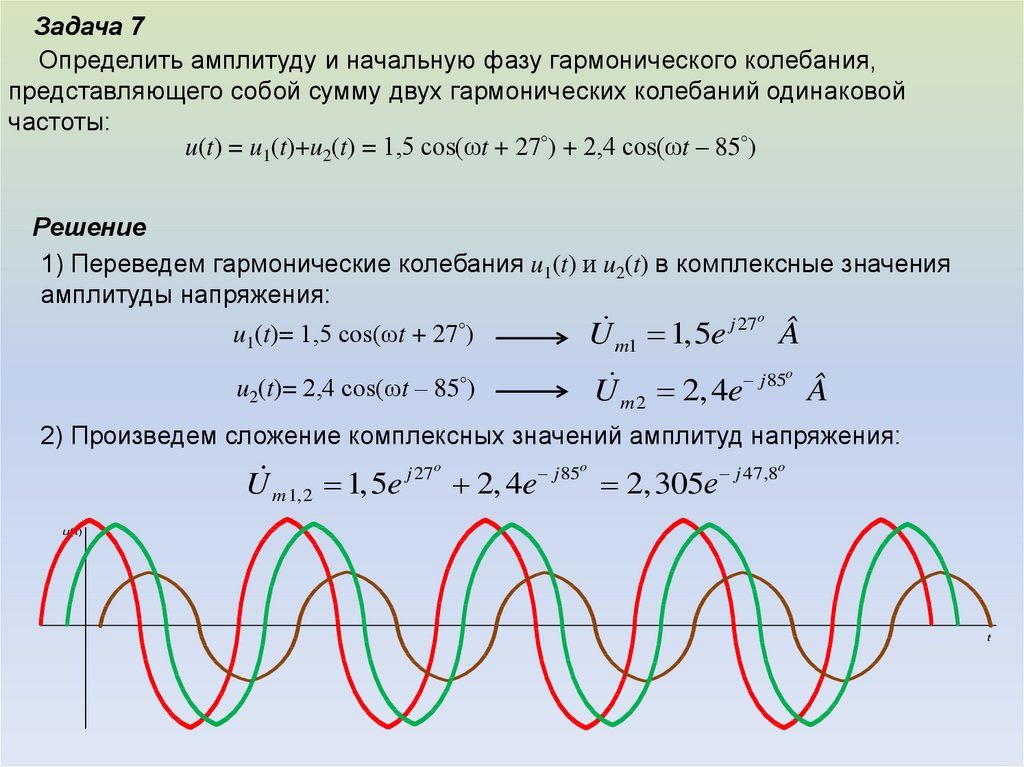
Задача 7Определить амплитуду и начальную фазу гармонического колебания,
представляющего собой сумму двух гармонических колебаний одинаковой
частоты:
u(t) = u1(t)+u2(t) = 1,5 cos(ωt + 27°) + 2,4 cos(ωt – 85°)
Решение
1) Переведем гармонические колебания u1(t) и u2(t) в комплексные значения
амплитуды напряжения:
u1(t)= 1,5 cos(ωt +
U m1 1,5e
27°)
j 27o
U m 2 2, 4e
u2(t)= 2,4 cos(ωt – 85°)
Â
j 85o
Â
2) Произведем сложение комплексных значений амплитуд напряжения:
U m 1,2 1,5e
j 27o
2, 4e
j 85o
2,305е
j 47,8o
u(t)
t
8.
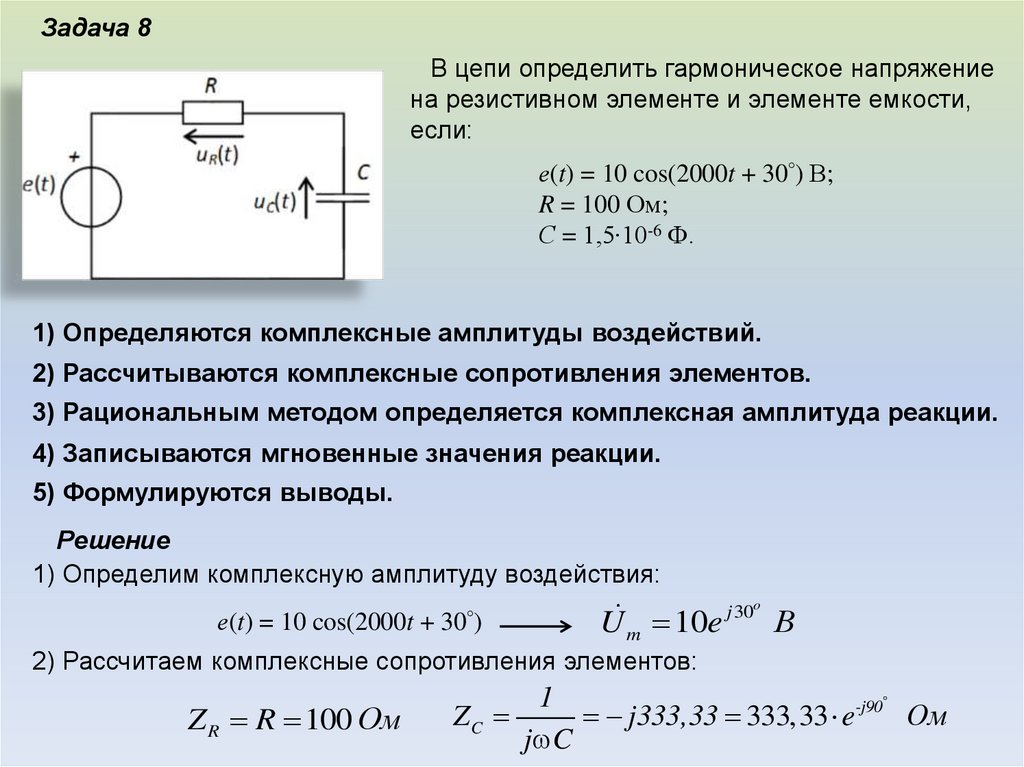
Задача 8В цепи определить гармоническое напряжение
на резистивном элементе и элементе емкости,
если:
е(t) = 10 cos(2000t + 30°) В;
R = 100 Ом;
С = 1,5∙10-6 Ф.
1) Определяются комплексные амплитуды воздействий.
2) Рассчитываются комплексные сопротивления элементов.
3) Рациональным методом определяется комплексная амплитуда реакции.
4) Записываются мгновенные значения реакции.
5) Формулируются выводы.
Решение
1) Определим комплексную амплитуду воздействия:
е(t) = 10 cos(2000t + 30°)
U m 10e j 30 В
o
2) Рассчитаем комплексные сопротивления элементов:
Z R R 100 Ом
1
-j90
ZC
j333,33 333,33 e
Ом
j C
9.
Схема замещения цепи будет выглядеть следующим образом:3) Произведем расчет комплексных амплитуд
реакции.
3.1) Определим эквивалентное комплексное
сопротивление:
Z RC
1
Z R ZC R
100 j 53 Ом
j C
Переведем в показательную форму:
Z RC 100 j 53 113е j 28
3.2) Определим комплексное амплитудное значение тока (первую реакцию).
Применим закон Ома в комплексной форме:
o
Um
10e j 30
j 58o
Im
0, 09е
А
j 28
Z RC 113е
3.3) Определим комплексное амплитудное значение напряжения на элементе
сопротивления (вторую реакцию).
U mR I m Z R 0, 09е
j 58o
100 9е
j 58o
В
10.
3.4) Определим комплексное амплитудное значение напряжения на элементеемкости (третью реакцию).
U mC I m ZC 0, 09е j 58 53e j 90 4, 77e j 32 В
o
o
o
Проведем проверку полученных результатов по второму закону Кирхгофа в
комплексной форме:
U m U mR U mС 0 U m U mR U mС
8,66 j5 10e
j 30o
9е
j 58o
4,77e
j 32o
4,77 j7,63 4,045 j 2,53 8,815 j5,1
4) Запишем мгновенные значения полученных реакций:
i(t) = 0,09 cos(2000t + 58°) А
uR(t) = 9 cos(2000t + 58°) В
uС(t) = 4,77 cos(2000t + 148°) В
5) Вывод: а) анализируя мгновенное значение напряжения на элементе
сопротивления можно видеть, что данный элемент частотно
независимый, и начальная фаза совпадает с начальной фазой тока;
б) анализируя мгновенное значение напряжения на элементе емкости
можно видеть, что начальная фаза отстает от начальной фазы тока
на 90°.







 physics
physics








