Расчет временных характеристик линейных электрических цепей

1.

ВОЕННАЯ
АКАДЕМИЯ
СВЯЗИ
2 кафедра
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
по учебной дисциплине
«Электроника, электротехника и схемотехника»
Тема № 4 Режим негармонических воздействий в
линейных электрических цепях
Занятие № 17 «Расчет временных характеристик
линейных электрических цепей»
Санкт-Петербург

2.

УЧЕБНЫЕ ВОПРОСЫ:
1. Анализ временных характеристик линейных
электрических цепей.
2. Контроль усвоения изученного материала.
ЛИТЕРАТУРА:
Бабкова Л.А., Киселев О.Н. Методические рекомендации к
практическим занятиям и руководство к лабораторным работам по
дисциплине «Основы теории цепей»: Учеб.пособие.– СПб.: ВАС, 2011.
2. Улахович Д.А. Основы теории линейных электрических цепей:
Учеб.пособие. – СПб.: БХВ-Петербург, 2009.
1.

3. Задача 1

1. Анализ временных характеристик линейных
электрических цепей.
Задача 1
Найти импульсную и переходную характеристики электрического
фильтра нижних частот с максимально плоской АЧХ, если известна
передаточная функция:
1
H ( p) 2
.
p 2 p 1
1. Определим изображение переходной характеристики
1
h ( p) H ( p).
p
h ( p)
1
p( p 2 p 1)
2
.

4.

2. Определим изображение импульсной характеристики:
g ( p) H ( p).
Таким образом изображение импульсной характеристики будет
иметь вид:
g ( p)
1
p 2 p 1
2
.
Воспользовавшись таблицей соответствий определяем графическое
изображение переходной и импульсной характеристик:

5.

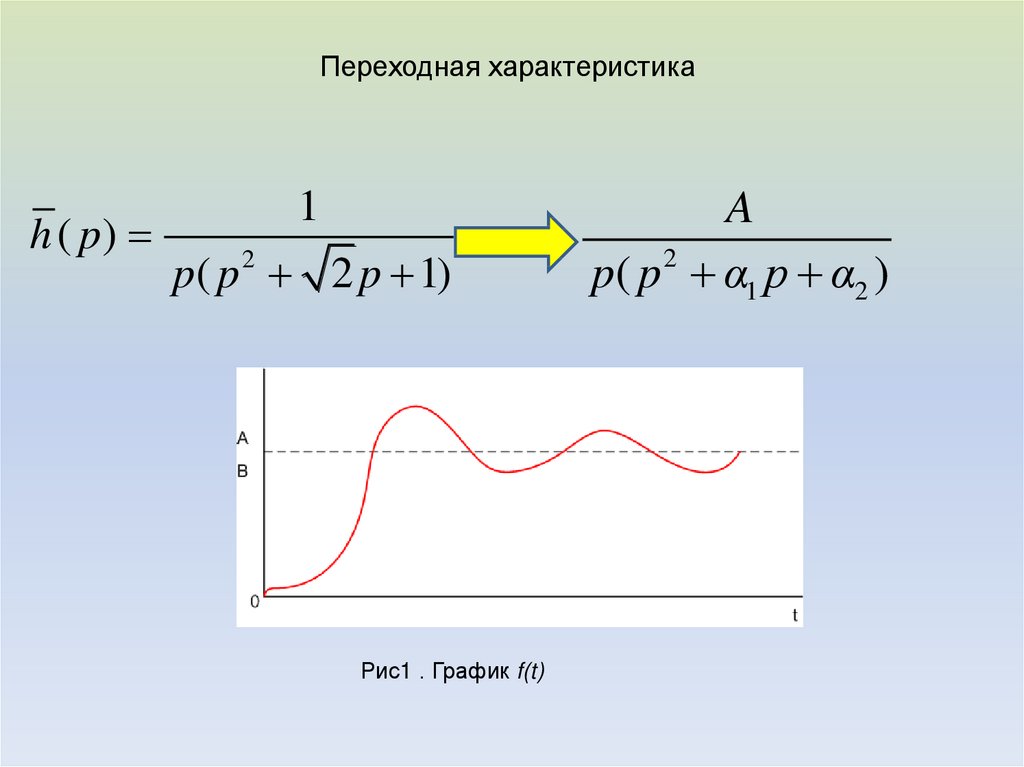
Переходная характеристика
h ( p)
1
p( p 2 2 p 1)
Рис1 . График f(t)
A
p( p 2 α1 p α2 )

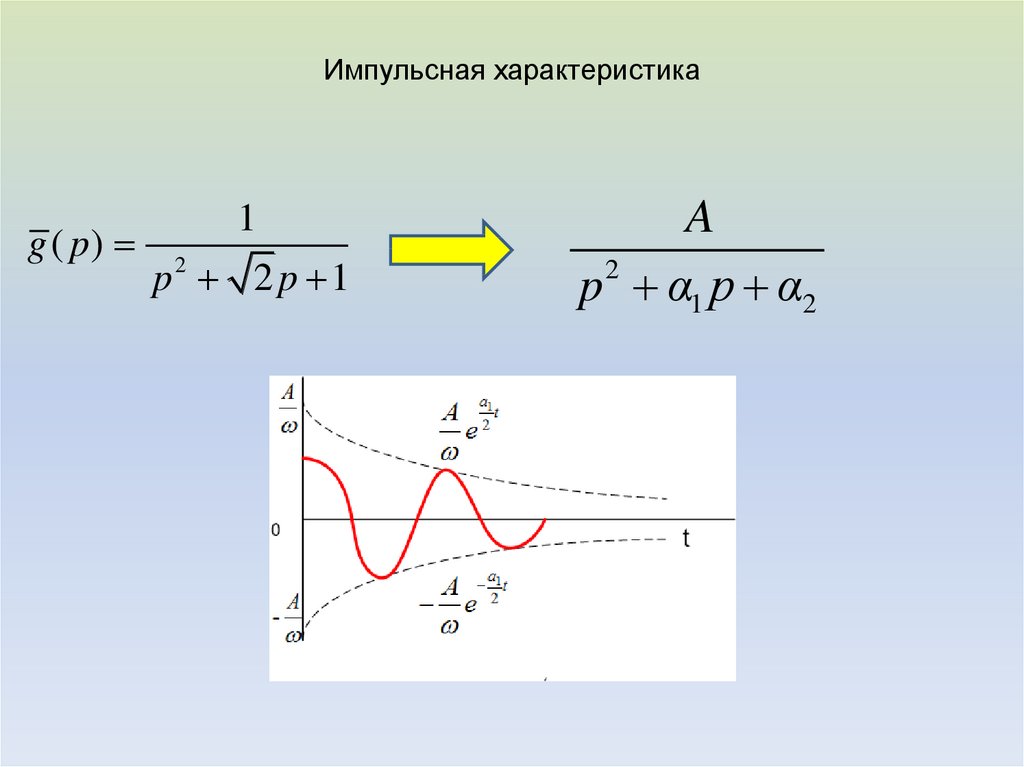
6. Импульсная характеристика

g ( p)
1
p2 2 p 1
A
p 2 α1 p α2

7. Задача 2

Найти импульсную и переходную характеристики цепи, если известна
ее передаточная функция:
181,8 p
H ( p) 2
p 1091 p 1,818 106
1. Определим изображение переходной характеристики
1
h( p ) H ( p )
p
2. Определим изображение импульсной характеристики:
g ( p) H ( p).
181,8 p
g ( p) 2
p 1091 p 1,818 106

8.

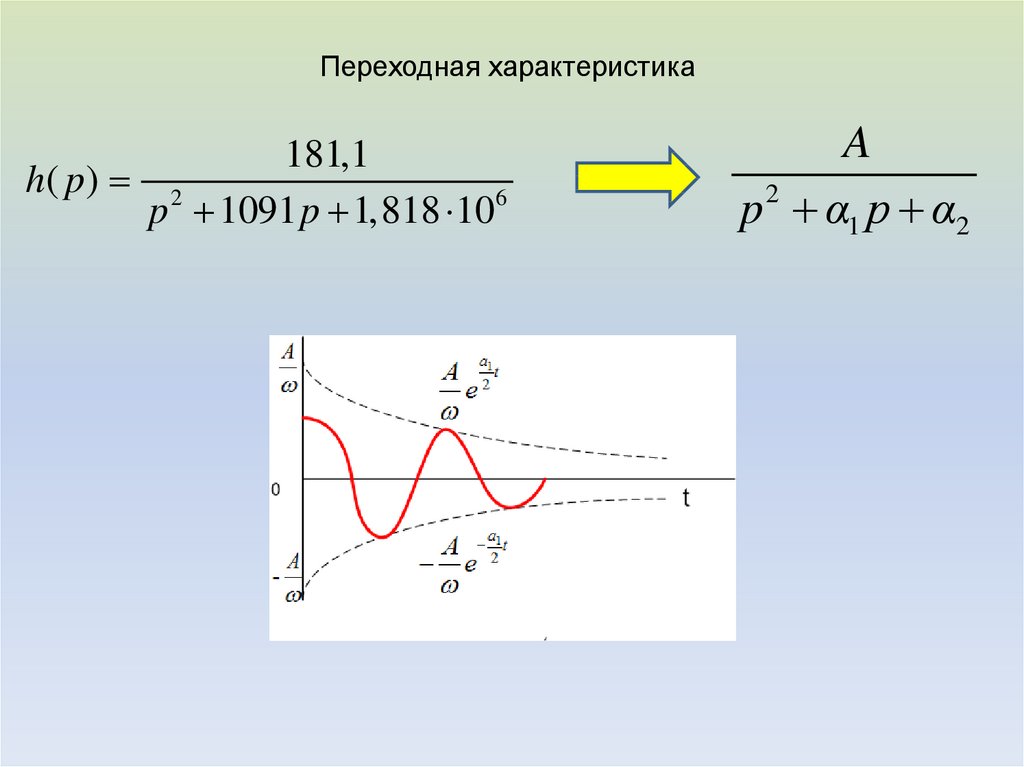
Переходная характеристика
181,1
h( p ) 2
p 1091 p 1,818 106
A
2
p α1 p α2

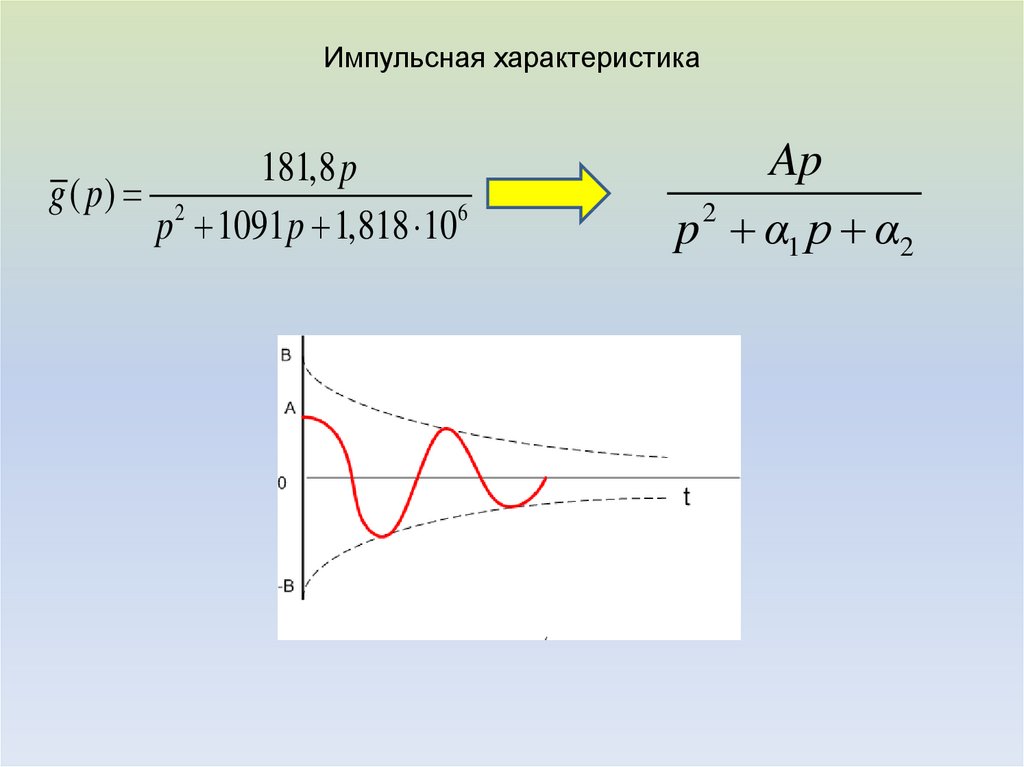
9. Импульсная характеристика

181,8 p
g ( p) 2
6
p 1091 p 1,818 10
Ap
p 2 α1 p α2

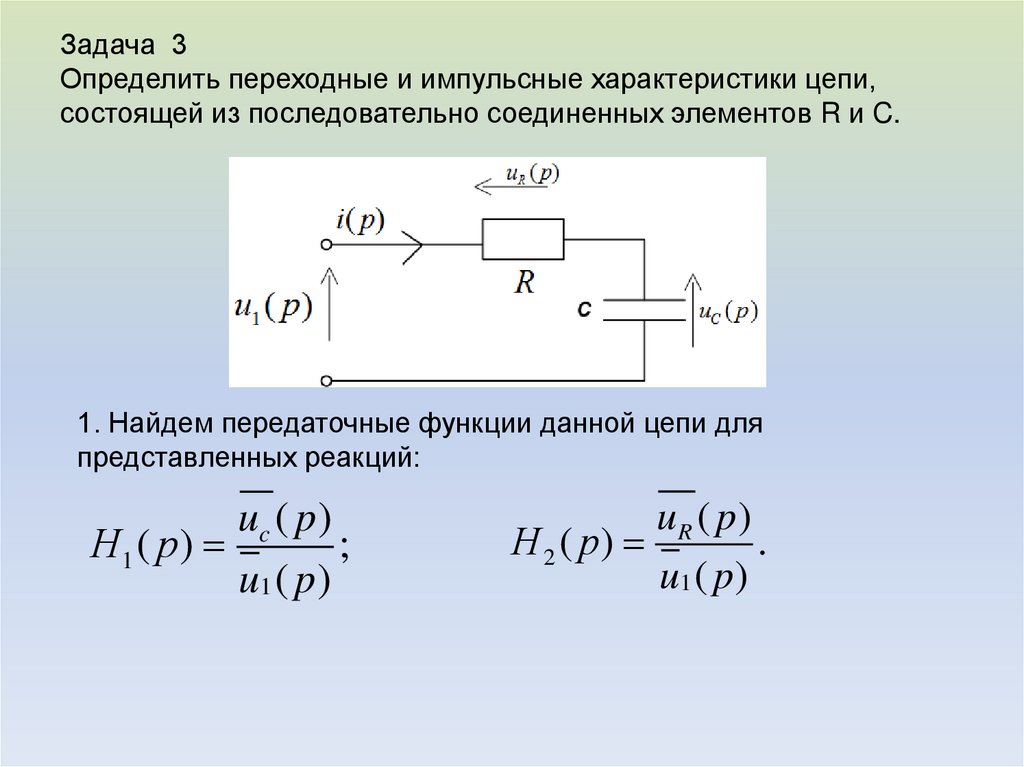
10. Задача 3 Определить переходные и импульсные характеристики цепи, состоящей из последовательно соединенных элементов R и C.

1. Найдем передаточные функции данной цепи для
представленных реакций:
uc ( p )
Н1 ( p )
;
u1 ( p )
uR ( p)
Н 2 ( p)
.
u1 ( p )

11. 2. Найдем значение реакции на элементах С и R.

1
u1 ( p )
1
u1 ( p )
uc ( p ) i ( p )
;
pC R 1 pC pRC 1
pC
u1 ( p )
u1 ( p ) pRC
uR ( p) i( p) R
R
.
1
pRC
1
R
pC

12. 3.Передаточная функция в операторной форме:

1
H1 ( p )
;
pRC 1
pRC
H 2 ( p)
.
pRC 1
4. Найдем изображения переходных характеристик:
H1 ( p )
1
hC ( p )
p
p ( pRC 1)
1
RC
1
p p
RC
H 2 ( p)
RC
1
h R ( p)
.
p
pRC 1 p 1
RC
;

13. 4. Изображение импульсных характеристик находим по соотношению:

g ( p) H ( p)
1
1
g C ( p ) H1 ( p )
RC ;
pRC 1 p 1
RC
1
pRC
1
g R ( p) H 2 ( p)
1
1 RC .
1
pRC 1
pRC 1
p
RC

14.

Спасибо за внимание!

15. Допустим, что к цепи приложено ступенчатое воздействие , изображение которого является функция

Допустим, что к цепи приложено ступенчатое воздействие
изображение которого является функция A
p
х(t ) A 1(t )
.
x (t )
0 при t 0;
x(t )
A при t 0.
A
t
0
Рис. 1. Ступенчатое воздействие
Тогда операторная передаточная функция будет иметь вид:
y ( p) y ( p)
y ( p)
H ( p)
p
.
A
x ( p)
A
p
(10)
,

16. Осуществляя L-преобразование выражения (7), т.е. найдем L-изображение переходной характеристики. В силу свойства линейности

Осуществляя L-преобразование выражения (7), т.е. найдем Lизображение переходной характеристики. В силу свойства линейности
преобразования Лапласа получаем:
1
h ( p) T ( p).
p
(11)
Это выражение совпадает со вторым сомножителем правой части (10)
и, следовательно, между операторной передаточной функцией и
изображением переходной характеристики h ( p) имеется следующая
взаимосвязь:
H ( p) ph ( p);
1
h ( p) T ( p).
p
(12)
(13)
Аналогично установим связь между H ( p ) и изображением
импульсной характеристики g ( p ) :
y (t )
g ( p)
;
Sи

17. Если же на цепь подается импульсное воздействие , изображение которого равно , то операторная передаточная функция,

Если же на цепь подается импульсное воздействие х(t ) Sи (t ) ,
изображение которого х ( p ) равно
, то операторная передаточная
и
функция, соответствующая этому воздействию, имеет вид:
S
y ( p) y ( p)
H ( p)
.
х ( p)
Sи
(14)
Это выражение совпадает с функцией изображения импульсной
характеристики цепи. Следовательно,
g ( p) H ( p).
(15)

18.

Рассмотрим связь между переходной и импульсной характеристиками
цепи. Не трудно заметить, что их изображения связаны соотношением
g ( p) ph ( p).
Проведя тождественное преобразование последнего равенства
(прибавив
h(0) h(0) ) получим:
g ( p) ph ( p) h(0) h(0).
ph( p) h( p)
Поскольку
представляет собой изображение
произвольной переходной характеристики, то исходное равенство
можно представить в виде
g ( p) h(0) L h / (t ) .
Переходя в область оригиналов, получаем формулу, позволяющую
определить импульсную характеристику цепи по известной
ее
/
переходной характеристике, g (t ) h(0) (t ) h (t ).
/
g
(
t
)
h
(t ).
Если h(0) 0 , то
Обратное соотношение между указанными характеристиками имеет
t
вид:
h(t ) g (t )dt.
0
(15)

19.

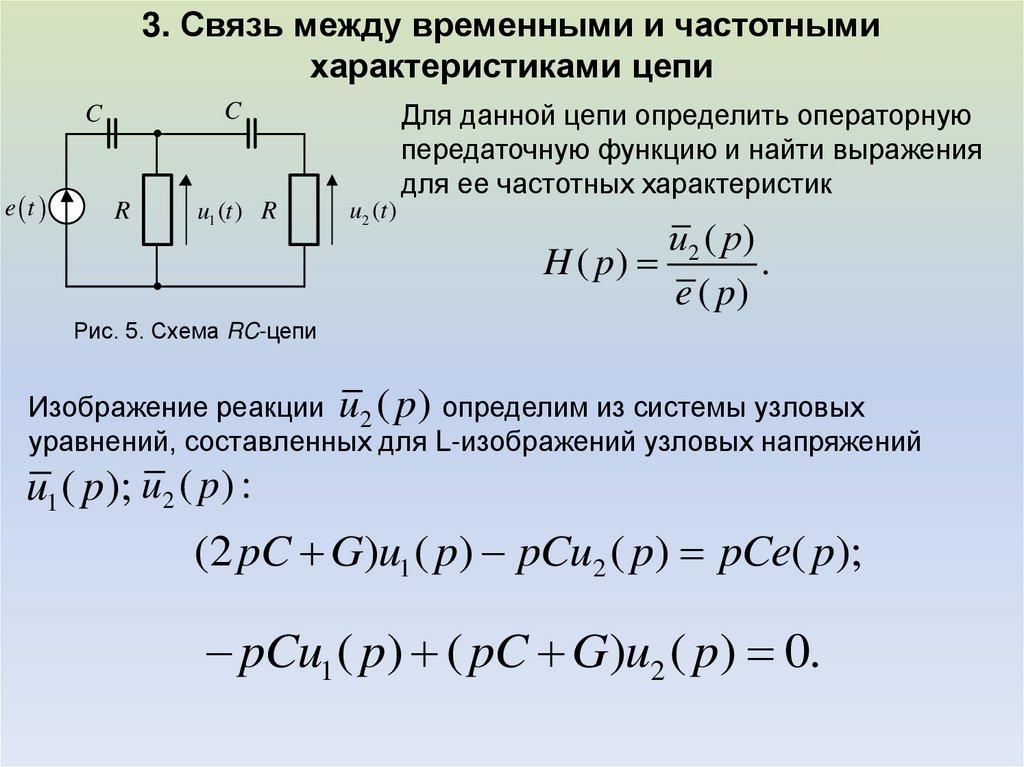
3. Связь между временными и частотными
характеристиками цепи
e t
Для данной цепи определить операторную
передаточную функцию и найти выражения
для ее частотных характеристик
C
C
R
u1 (t ) R
u2 (t )
и2 ( p )
H ( p)
.
e ( p)
Рис. 5. Схема RC-цепи
Изображение реакции u2 ( p) определим из системы узловых
уравнений, составленных для L-изображений узловых напряжений
u1 ( p ); u2 ( p) :
(2 pC G)u1 ( p) pCu2 ( p) pCe( p);
pCu1 ( p) ( pC G)u2 ( p) 0.

20. Отсюда

e ( p) p 2
u2 ( p )
;
2
G G
2
p 3p 2
C C
2
p
H ( p) 2
2
p 3 p
где для упрощения записи введено обозначение
G
.
C
Для нахождения комплексной передаточной функции положим в
последнем выражении p j . Тогда
H ( j ) 2
.
2
( ) j3
2

21.

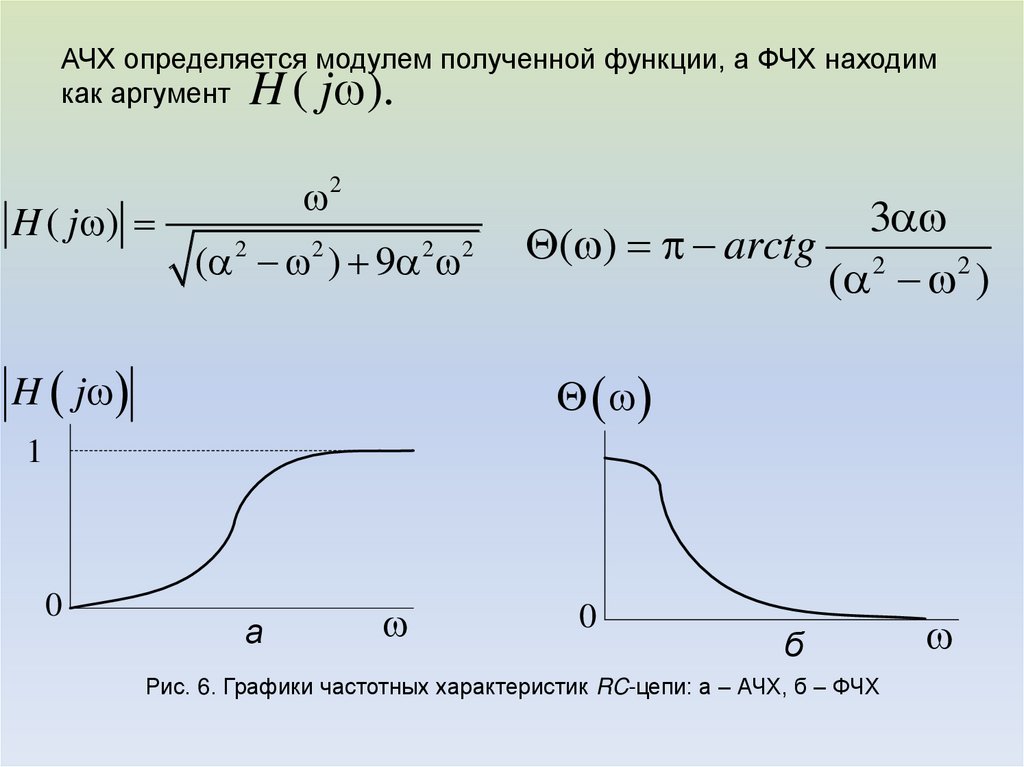
АЧХ определяется модулем полученной функции, а ФЧХ находим
как аргумент
H ( j ).
H ( j )
2
( 2 2 ) 9 2 2
H j
3
( ) arctg 2
( 2 )
1
0
а
0
б
Рис. 6. Графики частотных характеристик RC-цепи: а – АЧХ, б – ФЧХ

22.

ВЫВОДЫ:
1. Передаточная функция является L-изображением импульсной характеристики.
2. Передаточная
функция
является
дробно-рациональной
функцией
с
вещественными коэффициентами.
3. Полюсы устойчивой передаточной функции лежат в левой р-полуплоскости.
4. Степени полиномов числителей передаточной функции и квадрата АЧХ не
превышают степеней полиномов знаменателей; при невыполнении этого
свойства АЧХ на бесконечно больших частотах (ω → ∞) должна принимать
бесконечно большое значение, поскольку числитель в этом случае растёт
быстрее знаменателя.
5. Частотные характеристики цепи вычисляются по передаточной функции при
p = jω.
6. Квадрат АЧХ является чётной рациональной функцией переменной с
вещественными коэффициентами: H(jω) 2 = H(–jω) 2 .
7. По передаточной функции можно изобразить схему цепи.

23.

.
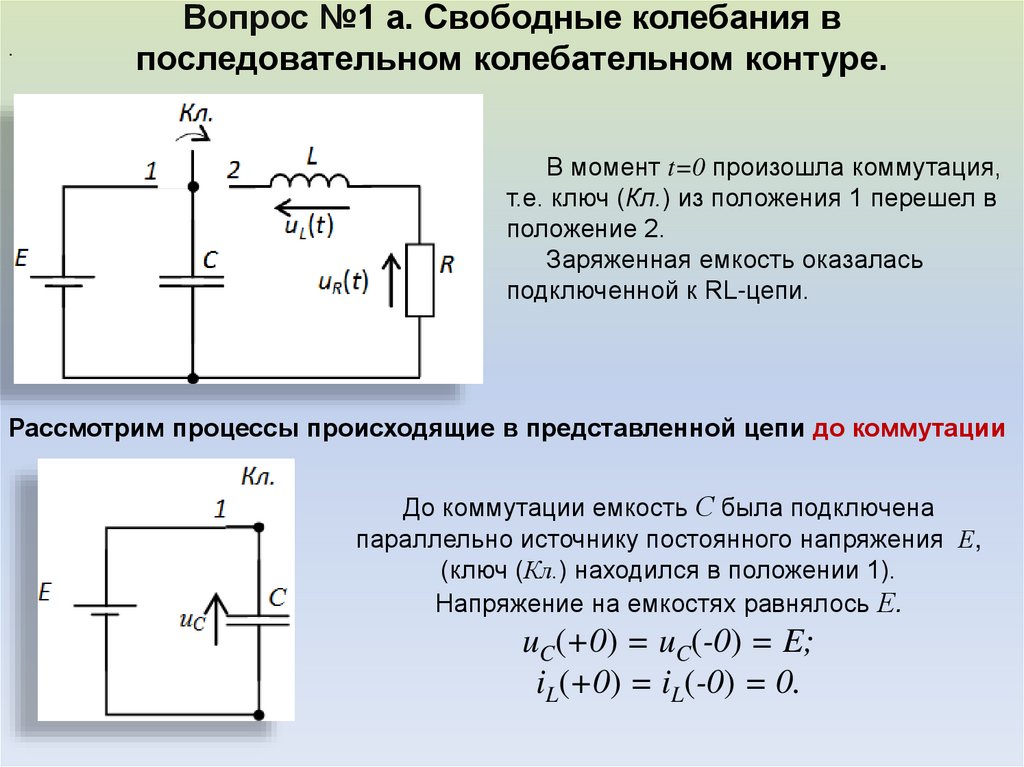
Вопрос №1 а. Свободные колебания в
последовательном колебательном контуре.
В момент t=0 произошла коммутация,
т.е. ключ (Кл.) из положения 1 перешел в
положение 2.
Заряженная емкость оказалась
подключенной к RL-цепи.
Рассмотрим процессы происходящие в представленной цепи до коммутации
До коммутации емкость С была подключена
параллельно источнику постоянного напряжения Е,
(ключ (Кл.) находился в положении 1).
Напряжение на емкостях равнялось Е.
uC(+0) = uC(-0) = E;
iL(+0) = iL(-0) = 0.

24.

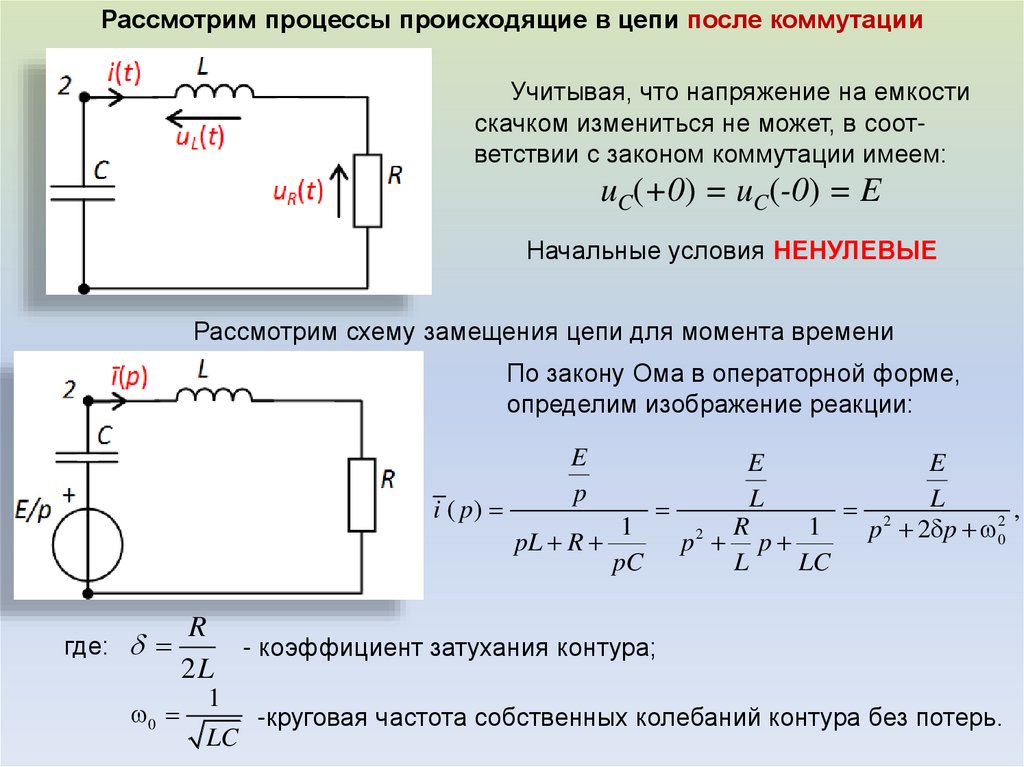
Рассмотрим процессы происходящие в цепи после коммутации
Учитывая, что напряжение на емкости
скачком измениться не может, в соответствии с законом коммутации имеем:
uC(+0) = uC(-0) = E
Начальные условия НЕНУЛЕВЫЕ
Рассмотрим схему замещения цепи для момента времени
По закону Ома в операторной форме,
определим изображение реакции:
E
p
E
E
L
L
i ( p)
2
,
2
1
R
1
p 2 p 0
pL R
p2 p
pC
L
LC
где:
0
R
- коэффициент затухания контура;
2L
1
LC
-круговая частота собственных колебаний контура без потерь.

25.

При анализе свободных и переходных колебаний в сложных цепях
изображение реакции y ( p ) представляет собой дробно-рациональную функцию
переменного p с вещественными коэффициентами, которую можно записать в
виде отношения двух полиномов:
M ( p) bm p m bm 1 p m 1 bm 2 p m 2 ... b0
y ( p)
N ( p)
p n a n 1 p n 1 a n 2 p n 2 ... a 0
По основной теореме алгебры полином степени n может быть разложен на n
простых сомножителей, т.е.:
N(p) = (p-p1) (p-p2),…, (p-pn),
где p1, p2, p3,…,pn – корни полинома N(p) или полюсы функции y ( p ) .
Полином также можно представить в виде произведения m сомножителей:
M(p) = (p-p01) (p-p02) (p-p03),…,(p-p0m).
где p01, p02, p03,…,p0m - корни полинома М(p) или нули функции y ( p ) .
В силу вещественности коэффициентов ai и bi нули и полюсы изображения y ( p )
могут быть вещественными и (или) комплексно-сопряженными.
Ясно, что дислокация полюсов y ( p ) определяет характер свободных и
переходных колебаний в анализируемой цепи.

26.

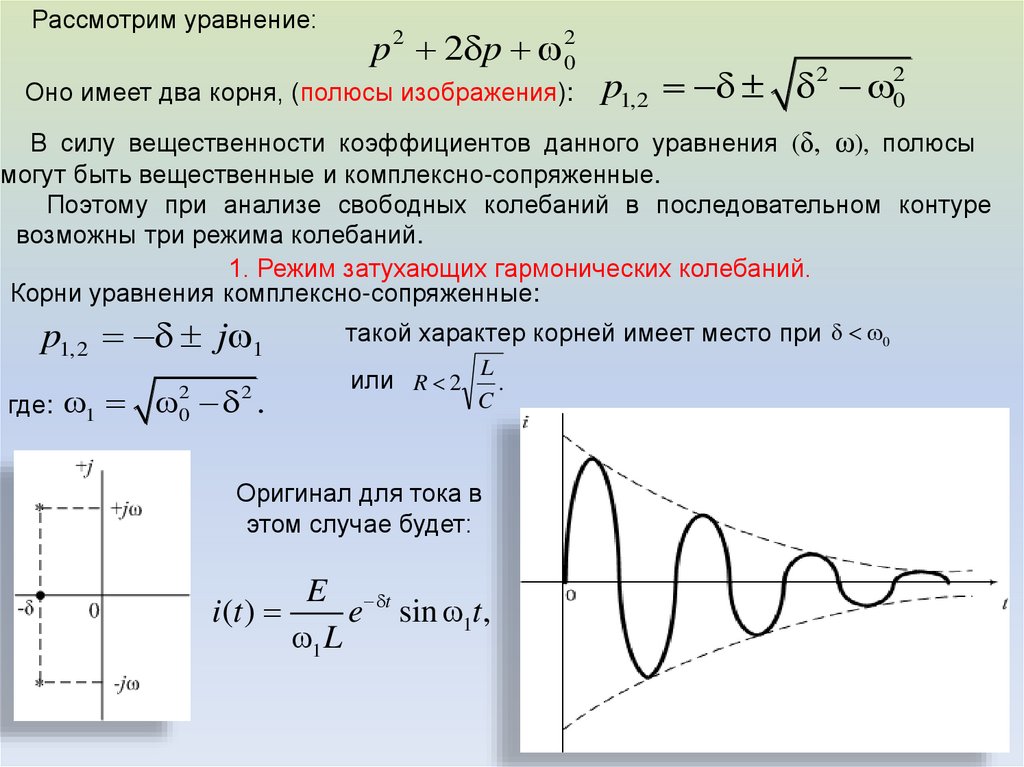
Рассмотрим уравнение:
p 2 2 p 02
Оно имеет два корня, (полюсы изображения):
p1,2 2 02
В силу вещественности коэффициентов данного уравнения (δ, ω), полюсы
могут быть вещественные и комплексно-сопряженные.
Поэтому при анализе свободных колебаний в последовательном контуре
возможны три режима колебаний.
1. Режим затухающих гармонических колебаний.
Корни уравнения комплексно-сопряженные:
p1,2 j 1
где:
1 02 2 .
такой характер корней имеет место при 0
или R 2
L
.
C
Оригинал для тока в
этом случае будет:
E t
i(t )
e sin 1t ,
1 L

27.

Амплитуда колебания убывает во времени по экспоненциальному закону,
поэтому процесс называют затухающим. Скорость убывания амплитуды
свободных колебаний определяется значением коэффициента затухания δ.
2
Частоту: 1 02 2 0 1 называют частотой собственных
0
затухающих колебаний контура. Она, как видно из формулы, всегда меньше
частоты собственных незатухающих колебаний контура w0 и зависит не только от
значений индуктивности и емкости контура, но и от значения его резистивного
сопротивления.
Период затухающих колебаний:
T
2
2
0
2
.
Коэффициент затухания связан с добротностью контура соотношением:
где: Q
R 0
.
2 L 2Q
0 L
- добротность последовательного контура.
R
Таким образом, колебания в контуре убывают тем медленнее, чем выше его
добротность.

28.

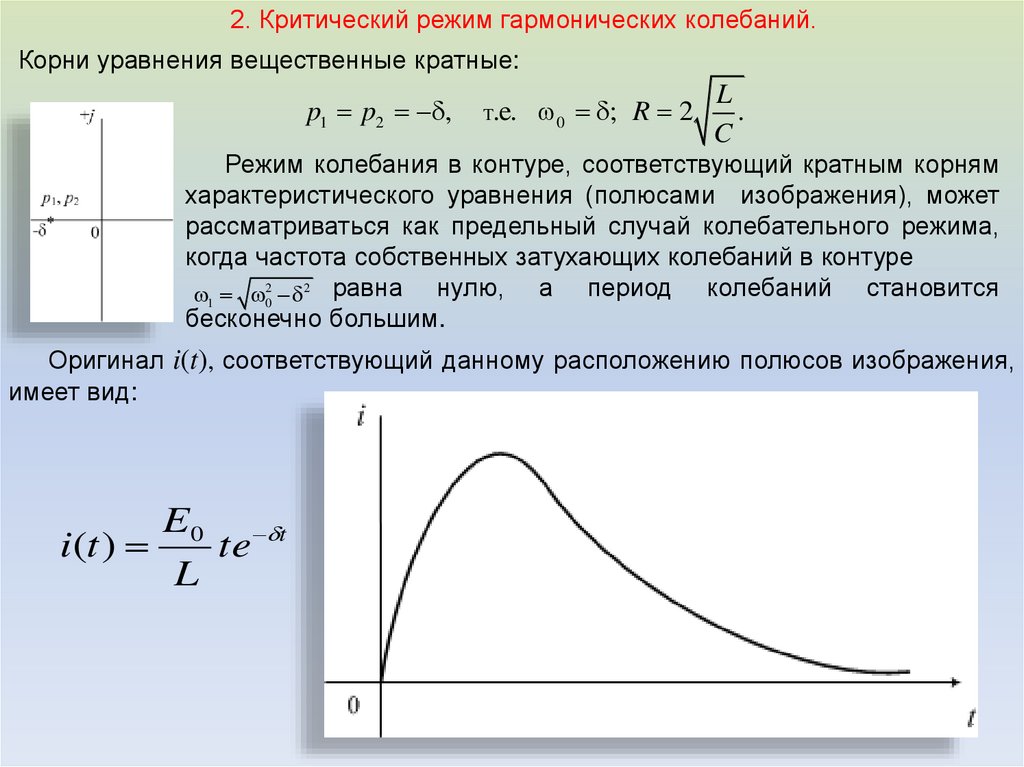
2. Критический режим гармонических колебаний.
Корни уравнения вещественные кратные:
p1 p2 ,
.e. 0 ; R 2
T
L
.
C
Режим колебания в контуре, соответствующий кратным корням
характеристического уравнения (полюсами изображения), может
рассматриваться как предельный случай колебательного режима,
когда частота собственных затухающих колебаний в контуре
нулю, а период колебаний становится
1 02 2 равна
бесконечно большим.
Оригинал i(t), соответствующий данному расположению полюсов изображения,
имеет вид:
E0 t
i(t )
te
L

29.

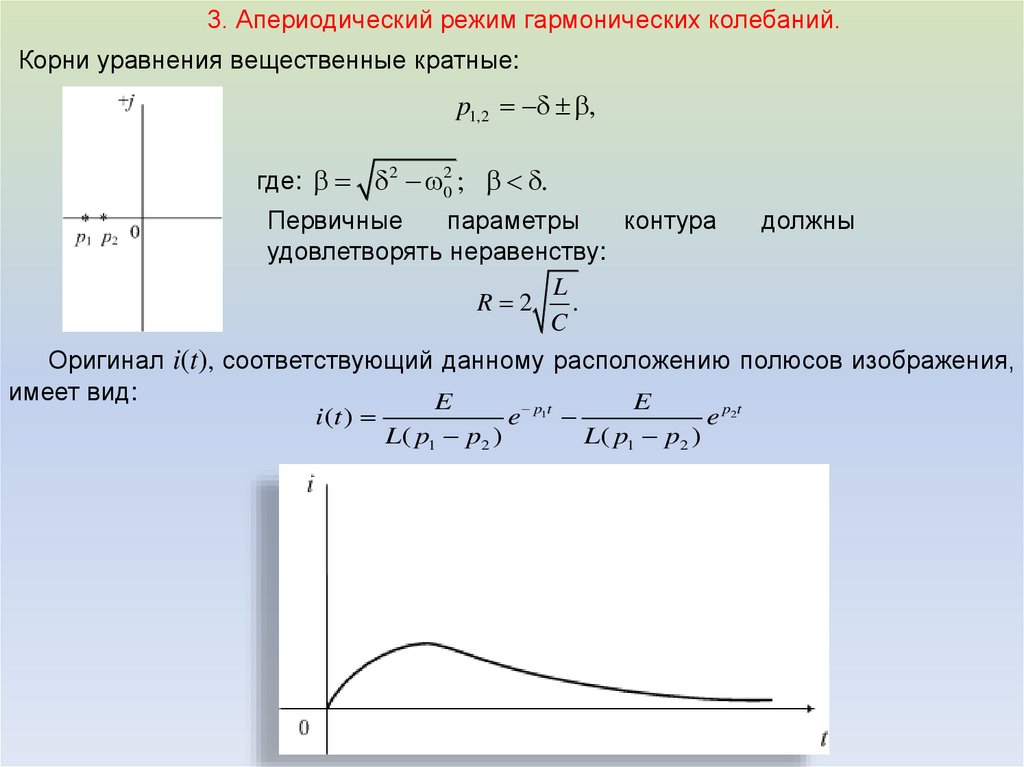
3. Апериодический режим гармонических колебаний.
Корни уравнения вещественные кратные:
p1,2 ,
где: 2 02 ; .
Первичные
параметры
контура
должны
удовлетворять неравенству:
L
R 2
.
C
Оригинал i(t), соответствующий данному расположению полюсов изображения,
имеет вид:
E
E
i (t )
L( p1 p2 )
e p1t
L( p1 p2 )
e p2t

30.

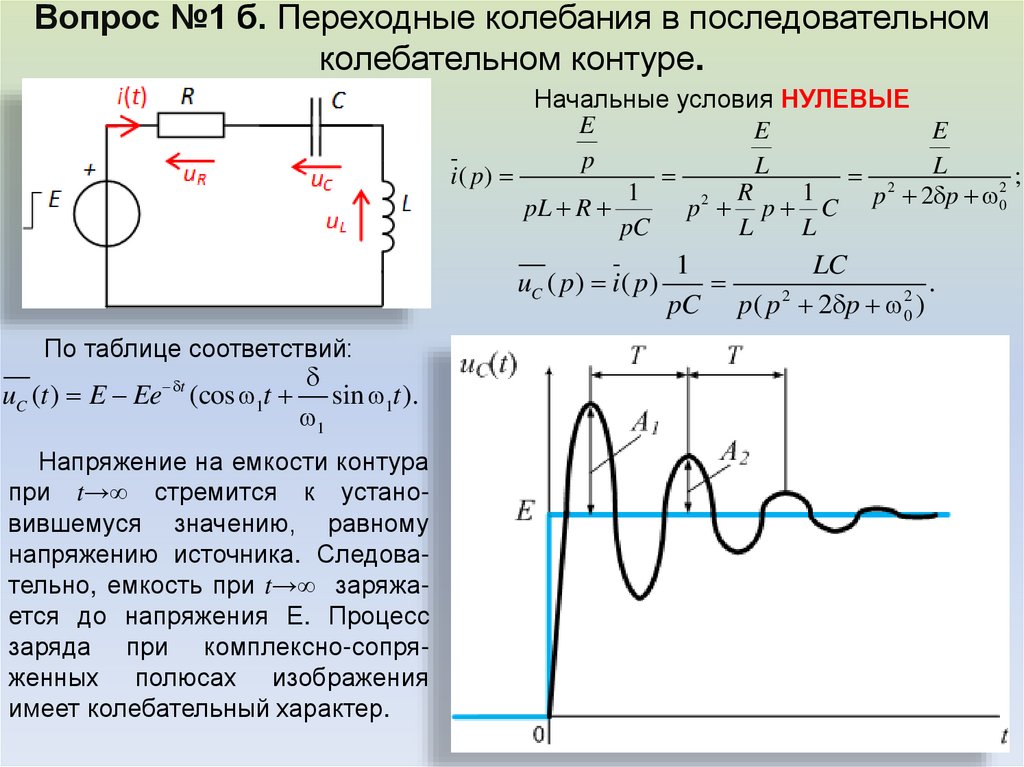
Вопрос №1 б. Переходные колебания в последовательном
колебательном контуре.
Начальные условия НУЛЕВЫЕ
E
E
E
p
L
L
i( p)
2
;
2
1
R
1
p
2
p
0
pL R
p2 p C
pC
L
L
uC ( p) i( p)
По таблице соответствий:
uC (t ) E Ee (cos 1t sin 1t ).
1
t
Напряжение на емкости контура
при t→∞ стремится к установившемуся значению, равному
напряжению источника. Следовательно, емкость при t→∞ заряжается до напряжения Е. Процесс
заряда при комплексно-сопряженных полюсах изображения
имеет колебательный характер.
1
LC
.
2
2
pC p( p 2 p 0 )

31.

Значение uC(t) в отдельные моменты времени превышают значения напряжения при большой добротности может почти вдвое превосходить ЭДС источника.
При t→∞ значения тока в контуре, напряжений на резистивном элементе и на
индуктивности контура стремятся к нулю, а напряжение на емкости - к ЭДС
источника. Следовательно, цепь переходит в режим постоянного тока. Процесс
установления колебаний происходит тем медленнее, чем выше добротность
контура. Для оценки времени установления можно воспользоваться полученной
ранее формулой:
ty
3 4, 6
,
что соответствует промежутку времени, по истечении которого амплитуда напряжения uC(t) отклоняется от установившегося значения не более чем на 0,05 или 0,01.
Вопрос №2 Свободные и переходные колебания в
параллельном колебательном контуре.
2.1 Свободные колебания в ПрКК
Начальные условия НЕНУЛЕВЫЕ
iL(+0) = iL(-0) = I0
uC(+0) = uC(-0) = u0

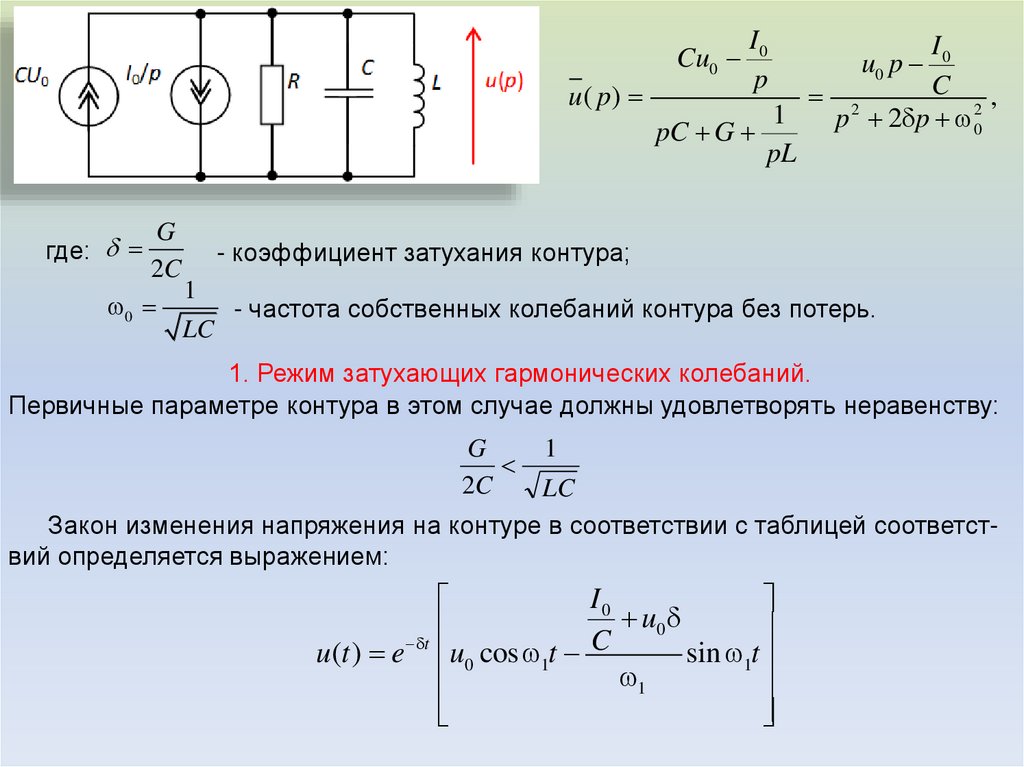
32.

I0
Cu0
p
I0
u0 p
C ,
u ( p)
2
2
1
p
2
p
0
pC G
pL
G
- коэффициент затухания контура;
2C
1
0
- частота собственных колебаний контура без потерь.
LC
где:
1. Режим затухающих гармонических колебаний.
Первичные параметре контура в этом случае должны удовлетворять неравенству:
G
2C
1
LC
Закон изменения напряжения на контуре в соответствии с таблицей соответствий определяется выражением:
I0
u
0
t
C
u (t ) e u0 cos 1t
sin 1t
1

33.

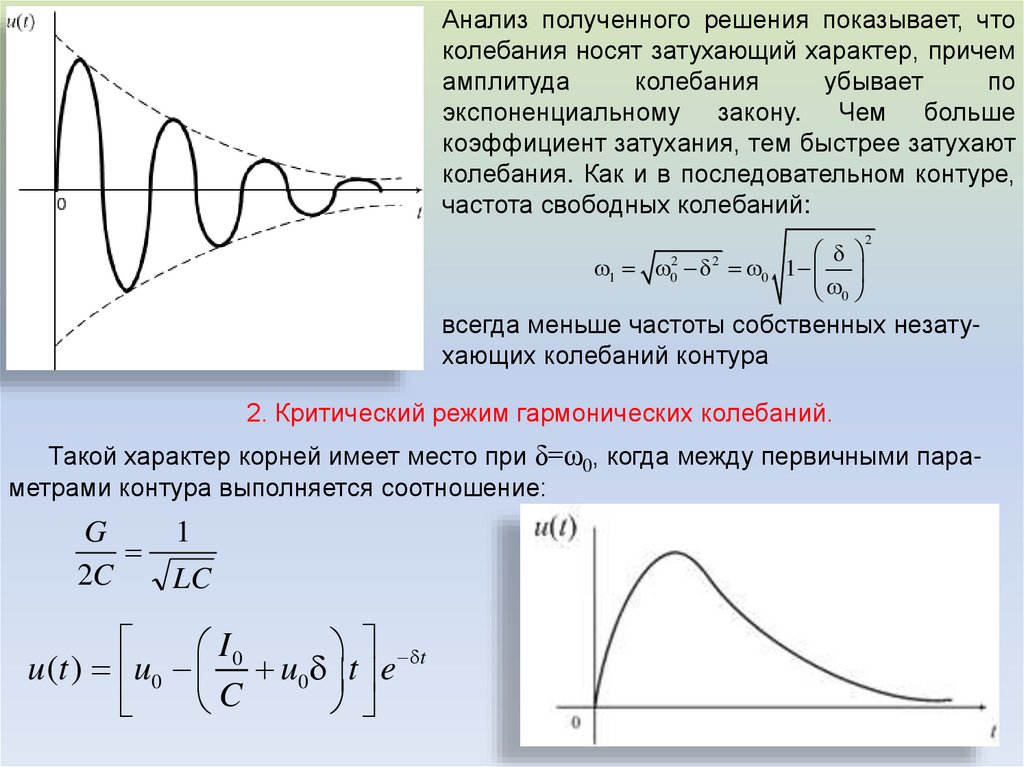
Анализ полученного решения показывает, что
колебания носят затухающий характер, причем
амплитуда
колебания
убывает
по
экспоненциальному закону. Чем больше
коэффициент затухания, тем быстрее затухают
колебания. Как и в последовательном контуре,
частота свободных колебаний:
1 0 1
0
2
0
2
2
всегда меньше частоты собственных незатухающих колебаний контура
2. Критический режим гармонических колебаний.
Такой характер корней имеет место при δ=ω0, когда между первичными параметрами контура выполняется соотношение:
G
2C
1
LC
I0
t
u (t ) u0 u0 t e
C

34.

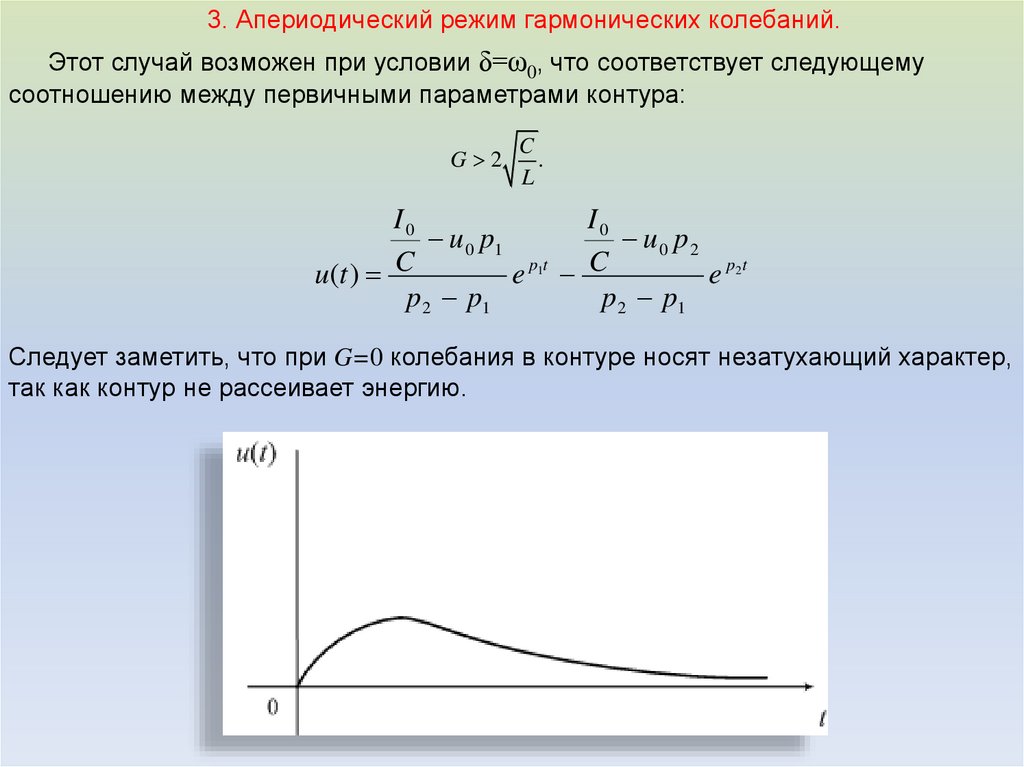
3. Апериодический режим гармонических колебаний.
Этот случай возможен при условии δ=ω0, что соответствует следующему
соотношению между первичными параметрами контура:
G 2
C
.
L
I0
I0
u 0 p1
u0 p2
u (t ) C
e p1t C
e p2t
p 2 p1
p 2 p1
Следует заметить, что при G=0 колебания в контуре носят незатухающий характер,
так как контур не рассеивает энергию.

35.

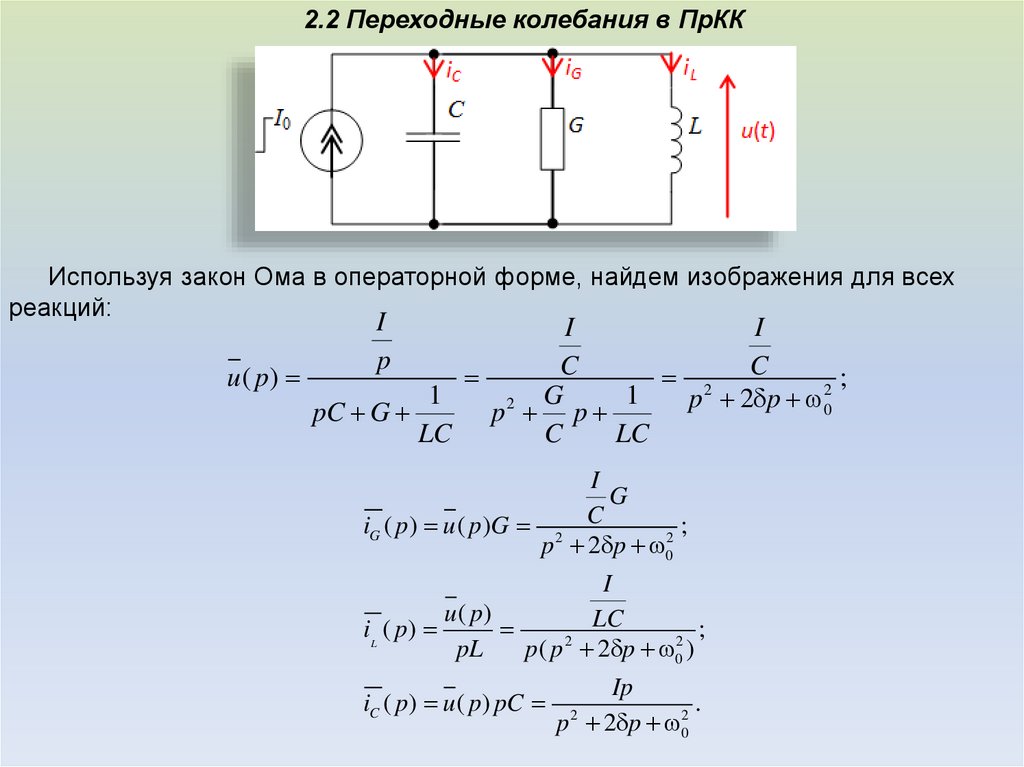
2.2 Переходные колебания в ПрКК
Используя закон Ома в операторной форме, найдем изображения для всех
реакций:
I
p
I
I
C
u ( p)
2 C
;
2
1
G
1
p 2 p 0
pC G
p2 p
LC
C
LC
I
G
C
iG ( p) u ( p)G 2
;
2
p 2 p 0
I
u ( p)
LC
iL ( p)
;
2
2
pL
p ( p 2 p 0 )
iC ( p ) u ( p) pC
Ip
.
2
2
p 2 p 0

36.

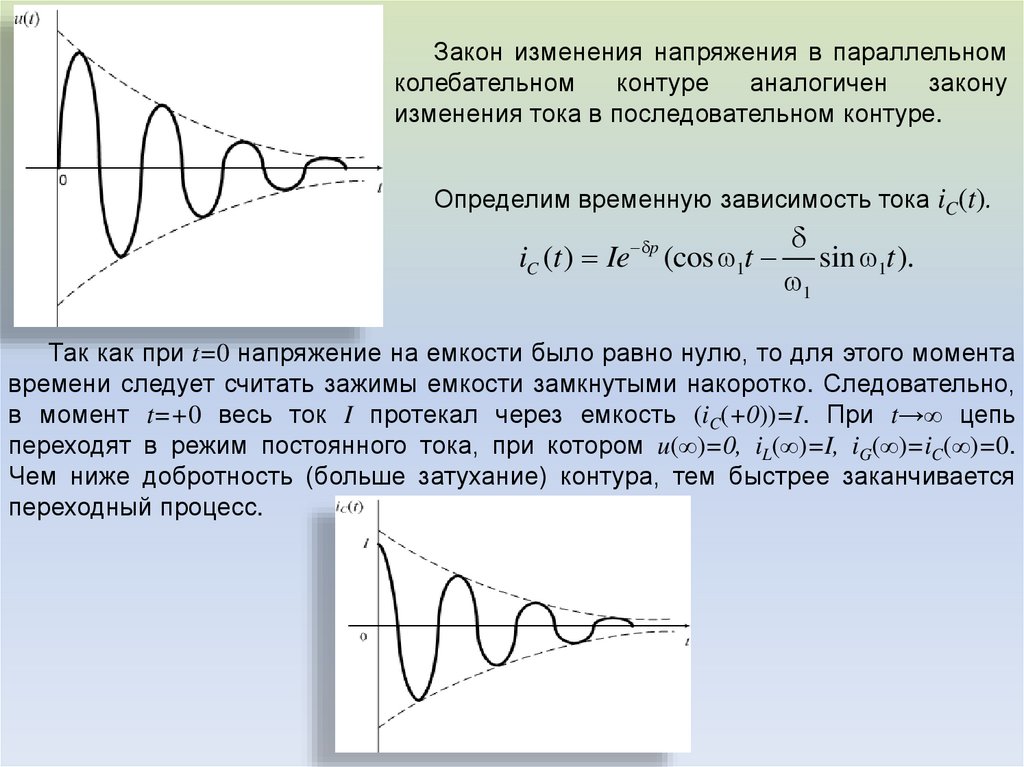
Закон изменения напряжения в параллельном
колебательном
контуре
аналогичен
закону
изменения тока в последовательном контуре.
Определим временную зависимость тока iC(t).
iC (t ) Ie
p
(cos 1t sin 1t ).
1
Так как при t=0 напряжение на емкости было равно нулю, то для этого момента
времени следует считать зажимы емкости замкнутыми накоротко. Следовательно,
в момент t=+0 весь ток I протекал через емкость (iC(+0))=I. При t→∞ цепь
переходят в режим постоянного тока, при котором u(∞)=0, iL(∞)=I, iG(∞)=iC(∞)=0.
Чем ниже добротность (больше затухание) контура, тем быстрее заканчивается
переходный процесс.