Similar presentations:
Классификация электрических цепей
1. Классификация электрических цепей
• 1. ЭЦ делятся на энергетические и информационные.• 2. Определим длину волны электрического сигнала.
• c , где c- скорость света (3 108 м с) , f - частота в Гц.
f
• При f 50 Гц, 6000 км. При f 50 мГц, 6 м.
• Если длина линий соизмерима или больше , то ЭЦ
называется цепью с распределенными параметрами
(длинные линии). В противном случае – с сосредоточенными параметрами.
• 3. Если R, L, C, M зависят от времени, то цепь называется
ЭЦ с переменными во времени параметрами. В противном
случае – с постоянными во времени параметрами.
2. Структура ЭЦ
• Структура – состав элементов цепи и способов ихсоединения.
• Ветвь – участок цепи, по которому течет один и тот же
ток.
• Узел – соединение трех и более ветвей.
• Контур – любой замкнутый путь, проходящий по
нескольким ветвям.
3. Виды соединений элементов
1. Последовательное соединениеR R1 R2 R3
экв
L L1 L2
экв
C
C1 C 2 (C1 C 2)
экв
4.
2. Параллельное соединениеR
R1 R2 (R1 R2)
экв
L
L1 L2 (L1 L2)
экв
C
C1 C 2
экв
5.
3. Смешанное соединениеСложные соединения могут не сводиться к последовательнопараллельным. Это ЭЦ мостиковой структуры, соединения
звездой и треугольником.
6.
Законы электрических цепей1. Закон Ома.
u
i , i u g, где g 1 - активная проводимость в См.
r
r
i, u - мгновенная сила тока и мгновенное напряжение.
2. Первый закон Кирхгофа.
ik 0.
Алгебраическая сумма токов в узле равна нулю.
i1 i2 i3 i4 0.
7.
3. Второй закон Кирхгофа.В замкнутом контуре ЭЦ алгебраическая сумма мгновенных значений ЗДС
равна алгебраической сумме мгновенных значений напряжений на элементах
контура.
m
n
ek uk
k 1
k 1
При составлении уравнений необходимо:
1) выбрать условно положительное направление I и u в элементах цепи;
2) выбрать положительное направление обхода контуров;
3) e и u считать положительными, если их направление совпадает с направлением обхода, в противном случае - отрицательными.
u2
Принято направление обхода - по часовой стрелке.
Тогда:
u1
e1 e2 u1 u2 u3.
e2
e1
u3
8.
4. Закон Джоуля - Ленцаp
Пусть действуют i и u. Определим мгновенную мощность .
Элементарная работа тока и напряжения за время dt - dA u i dt.
t2
Работа : A uidt. Мгновенная мощность : p dA ui.
dt
t1
Средняя мощность за промежуток времени от t до t :
1 2
t2
p 1 pdt.
ср t t
2 2 t1
Параметры элементов ЭЦ
Все элементы делятся на активные (источники ЭДС, тока) и пассивные (R, L, C).
9.
Гармонические воздействияЭто синусоидальные и косинусоидальные воздействия.
e(t) E sin( t ), i(t ) I sin( t ),
m
i
m
e
где E , I
m m
- амплитудные
значения ЭДС и тока.
t
e,i
- фаза,
e,i
- начальная фаза, -- круговая частота,
2 f .
( t ) ( t ) const.
e
i
e i
Разность фаз равна разности начальных фаз.
Разность фаз:
10.
Источники энергии постоянного тока1. Генераторы ЭДС
Это гальванические элементы, аккумуляторы, электрические машины – генераторы постоянного тока.
U
R R
0 н
0
U
Внешняя характеристика источника ЭДС характеризует изменение напряжения
U f (I ).
н
н
н
По второму закону Кирхгофа E U I R ,
E
U
н
U E I R .
н
н 0
н 0
откуда
U U холостого
Строим эту характеристику.
хх
хода ( I 0), I I короткого замыкания (U 0).
н
н
кз
Мощность, теряемая в источнике
E
Если R 0,
0
источник ЭДС энергии не расходует
и не нагревается.
I
I
E
кз R
0
н
н
P U I I 2R .
0н н 0
11.
2. Генераторы токаЭто, например, фотоэлементы.
I
ист
g
0
I
g
н
н
U
Внешняя характеристика источника тока I f (U ).
н
Её можно получить из 1 закона Кирхгофа в виде
н
I I
U g
н ист н 0
I
и построить графически,
используя режимы холостого хода и короткого
замыкания.
н
I
ист
U
I
ист
g
0
н
н
12.
Условия взаимного эквивалентного преобразованиягенераторов
В качестве критерия эквивалентности источников принимается совпадение их
внешних характеристик. Внешняя х-ка источника ЭДС U E I R (1),
источника тока - I I
н
ист
U g
н 0
(2).
н
н 0
Перейдем от источника ЭДС к эквивалентному источнику тока.
Е U
н E Uн
I
Из (1)
н
R
R R
0
0
0
(3).
Приравнивая, почленно, слагаемые правой части (2) и (3), получим:
E
1
I
; g .
ист R
0 R
0
0
Это условия перехода от генератора ЭДС к генератору тока. Переход от генератора тока к генератору ЭДС осуществляется по формулам:
I
1
E ист ; R .
0 g
g
0
0
13.
Действующее значение гармонических функцийДействующее значение переменного тока равно такому постоянному току,
который в одинаковом сопротивлении выделяет такое же количество тепла, что
и переменный ток.
i
r
r
I
dQ
kri2(t )dt.
пост
Для переменного тока, количество тепла, выделяемого за период T
:
T
T 2
Q
kri (t )dt kr i 2 (t )dt.
Q
krI 2T .
Для
постоянного
тока
перем
пост
0
0
T
2
1
Q
Q
.
По определению
перем
пост Отсюда I T I (t )dt . Аналогично
0
T
T
1 2
1 2
E
e (t )dt, U
u (t )dt .
T0
T0
T
1
2
Если функция синусоидальная e(t ) E sin t
, то E E sin 2 t dt.
m
T0 m
Элемент тепла, выделяемого при постоянном токе
Интегрируя, получим
E
E m.
2
Аналогично
Действующее значение величины в
I
U
m
I
,U m.
2
2
2 раза меньше амплитудного.
14.
Векторные диаграммыСинусоидальные токи, напряжения и ЭДС можно изображать вектором, вращающимся против часовой стрелки с угловой частотой , причем длина
этого вектора равна амплитудному (действующему) значению I , U , E. Пусть ЭДС
e E 2 sin( t ), где
- начальная фаза, t , если t меняется.
e
e
e
e
E (E )
m
U
I
Пусть есть 2 синусоидальные функции
u U 2 sin( t ), i I 2 sin( t ).
u
i
Если const, то сдвиг по фазе const.
u i
Всегда , а не наоборот. В нашем случае
u i
говорят, что U опережает I ( 0).
Совокупность векторов, характеризующих процессы в
ЭЦ, построенных с соблюдением их правильной ориентации относительно друг друга, называется векторной
диаграммой (ВД).
15.
1-ый закон Кирхгофа при синусоидальном воздействииn
ik 0.
k 1
Для мгновенных значений
i
2
Пусть имеем участок цепи
По 1 закону Кирхгофа i i i .
1
i
i
1
На векторной диаграмме суммируем геометрически
действующие значения токов I , I
и получаем
3
2 3
вектор I .
I
I
I
1
I
1
2
I
1
I
2
Для действующих значений, 1 закон Кирхгофа
записывается в векторном виде I I I , а не
3
I
3
1
I I I .
1 2 3
2
3
Пример
I , I , I равны, соответственно, 3 А, 10 А, 6 А. Найти ток I .
1 2 3
I
2 3
3
I I
2 3
I
2
I
1
U
I
Из ВД
I I 2 (I I )2 5 А.
1
2 3
16.
2 закон Кирхгофа при синусоидальном воздействииU U1 U 2 U 3.
Рассмотрим участок ЭЦ:
U
1
U
U
2
3
но не
U U U U .
1 2 3
U
Приложенное напряжение равно геометрической сумме напряжений на отдельных
участках цепи.
Пример
U
U , U , U равны, соответственно, 4 В, 15 В, 12 В. Найти U .
1 2 3
2
U U
2 3
U
I
U
1
U
3
U U 2 (U U )2 5 В.
1
2 3
17.
Электрическое сопротивление при синусоидальномвоздействии
i
r
u
i , p ui,
r
где p - мгновенная мощность.
u U 2 sin( t ),
u
u U
i
2 sin( t ) (1). С другой стороны i I 2 sin( t ) (2). Сравним (1) и (2).
i
u
r r
U - закон Ома для действующих значений для резистора. ,
I
т. е. 0.
u i
u i
r
u
Для синусоидального воздействия
Таким образом, ток и напряжение на резисторе – синфазны.
Определим мгновенную мощность:
p U 2 sin( t ) I 2 sin( t ) UI[1 cos 2( t )].
u
i
u
Средняя мощность за период
Выводы:
T
1T
1T
Pср P p dt [ UIdt UI cos 2( t )dt 1 UIT UI .
u
T0
T 0
T
0
1) p=0, когда i или u равно 0;
18.
u(t ), i(t ), p(t )p(t )
u(t )
2UI
i(t )
Графики построены при U I 0.
t
19.
2) p- синусоидальная функция удвоенной частоты;3) p>0, так как sin
2
- положительная величина.
Мощность всегда положительна, т. е. вся мощность, потребляемая резистором из
цепи, выделяется на нём в виде тепла.
Ёмкость при синусоидальном воздействии
du
du
i dq c c u dc c c .
c dt
c dt
dt
dt
Таким образом,
мгновенных значений. Отсюда найдём
1T
u u (0) i dt
c c
c0c
du
i c c
c
dt
uc :
- закон Ома для
uc
t
1
du i dt, duc 1 icdt,
c cc
uc (0) c 0
- закон Ома для мгновенных значений.
Мгновенная мощность:
p u i .
cc
2 sin( t ), Тогда:
c
u
U
du
U
i c c c U 2 cos( t ) c 2 sin( t ) c 2 sin( t ) (1).
u 2 xc
u 2
c
c
u
1
dt
c
Пусть uc изменяется по синусоидальному закону: u U
c
20.
Но, с другой стороны, i Ic
c
2 sin( t ) (2).
u
Сравним (1) и (2) по амплитуде:
U
I c - -закон Ома для действующих значений. x 1 - реактивное сопротивление
c x
c c
c
1
c - реактивная проводимость ёмкости.
ёмкости. b
c x
c
, u i ,
x ,b
Сравнивая
фазы,
получим:
c c
i
u 2
2
x
.
c
b
т. е. на ёмкости ток опережает напряжение на
c
2
I
На ёмкости I и U
c
c
U
c
c
находятся в квадратуре.
Мгновенная мощность:
p u i U c 2 sin( t u ) Ic 2 cos( t u ) U c I c sin 2( t u ).
cc
T
1
Средняя мощность: P P p dt 0.
ср
T0
Идеальная ёмкость активной мощности не потребляет, т. е. не преобразует
электромагнитную энергию в тепловую. При положительной полуволне мгновенной
мощности энергия запасается в С, при отрицательной – возвращается в источник.
21.
U (t ), I (t ), p(t )u (t )
c
p(t )
t
i (t )
c
График построен при U 0.
22.
Примерi
R
C
u 100 2 sin( t 30o ) В, x 10 Ом.
c
c
L
U
100
I I c
10 А;
c x
10
c
R
кат
Найти i.
i 10 2 sin( t 30o 90o ) А.
Индуктивность
L
Реальная индуктивность
L
«Идеальная» индуктивность
L создает магнитный поток L . Если все витки пронизываются потоком
то потокосцепление w L , где w - число витков.
L
Ток i
Опыт показывает, что наведённая ЭДС прямо пропорциональна скорости изменения
потокосцепления контура
L
d
e L.
L
dt
Знак «-» объясняется тем, что положительное направление отсчёта для наведённой
ЭДС и положительное направление линий магнитной индукции, пронизывающих
контур при возрастании потока, принято связывать правилом правого винта.
23.
Из опытов известно, что если катушка без сердечника илисердечника практически
не зависит от потока (магнитодиэлектрик),то потокосцепление пропорционально току:
Li
L
где L - индуктивность.
L,
d
L,
Так как e
L
dt
di
то e L L . Учтем, что u e .
L
L
L
dt
Тогда u L
L
di
L
dt
- закон Ома для мгновенных значений для индуктивности. Так же, как и для ёмкости,
связь между током и напряжением – дифференциальная.
Интегрируя закон Ома для индуктивности, получим закон Ома в интегральной форме:
1T
i i (0) u dt, где i (0) - ток в индуктивности в нулевой момент времени.
L L
L0 L
L
Случай синусоидального воздействия
Пусть i I
L
L
2 sin( t ).
i
Отсюда
u L L LI 2 cos( t ) x I sin( t ) (1),
L
L
i
L L
i 2
dt
di
С другой стороны:
U
L
L -закон Ома для
u U 2 sin( t ) (2). Сравнивая (1) и(2), получим: I L
x
L
L
L
u
L
1 1
b
для действующих значений. x L - индуктивное сопротивление, L x L
L
L
- индуктивная проводимость.
U
24.
x ,bL L
b
L
x
Сравним начальные фазы (1) и (2).
L
. , т. е. напряжение на индуктив-
U
L
u
i 2
u
i
2
ности опережает ток на 90o. Ток и напряжение находятся в
квадратуре.
I
Мгновенная мощность на индуктивности:
L
p u i I 2 sin( t ) I x 2 cos( t ) I LU L sin 2( t i ).
LL L
i
L L
i
1T
Активной мощности индуктивность не потребляет, т. к. P pdt 0.
T0
Пример
o
R=3 Ом, x 1 Ом, x 5 Ом, i 2 2 sin( t 25 ). Найти
C
L
u ,u ,u .
R C
L
R L C
U IR 2 3 6 В, u 6 2 sin( t 25o ); U I x 10 В, u 10 2 sin( t 25o 90o );
R
R
L L L
L
U I x 20 В, u 20 2 sin( t 25o 90o ).
C C C
C
25.
u (t ), i (t ), p(t )L
L
u (t )
L
i (t )
L
График построен при I 0.
p(t )
26.
Установившиеся процессы в ЭЦ присинусоидальном воздействии
(классический метод расчёта)
Последовательное соединение R, L, C
R C
L
Дано : i I 2 sin t,
i
U
u
L
R, L, C, , xC xL .
Из ВД: U U U U
U
R
R
L
C
Найти u.
2
или U U 2 (U U ) .
Разделив обе части выражения на I ,
R
L
C
получим
U U
L C U
2
2 - полное сопротивление цепи.
z
R
(
x
x
)
U
L
C
U
I
C
U I R, U I x , U I x . Фазовый сдвиг:
R
L
L C
C
U U
x x
arctg L C arctg L C . Окончательно:
U
R
R
x x
u I 2 R 2 ( x x ) sin( t arctg L C ).
L C
R
27.
Характер цепи переменного токаR C
U
L
L
U
1. Пусть L
U
I
U
R
lim
.
max
2
2. Индуктивное и емкостное сопротивления равны.
L
U U R U
C
U
1
, 0, т. е. U опережает I .
c
Характер цепи – индуктивный.
U
C
U
Фазовый сдвиг: arctg
1
c .
R
L
I
1
x x , L . U и I совпадают по фазе ( 0).
L C
c
Такой режим называется резонансным.
3. Пусть L
L U
R
U
U
C
1
, 0,
c
т. е. U опережает I .
Характер цепи емкостной.
28.
Треугольники напряжений и сопротивленийИзобразим треугольник напряжений
U Iz
I ( x x ) U - реактивная составляющая напряжения. U U sin .
L C
Р
Р
U IR U - активная составляющая напряжения. U U cos .
R
А
А
Кроме того, U U 2 U 2 .
А
Р
Разделим стороны треугольника напряжений на ток I
и получим треугольник
сопротивлений:
z
R
x x x
L C
z R 2 x 2 - полное сопротивление цепи.
R - активная составляющая сопротивления цепи.
x - реактивная составляющая сопротивления цепи.
R z cos , x z sin .
29.
Параллельное соединение R, L, Ci
Дано: u U 2 sin t, R, L, C, . Найти i.
i i
i
R L C
Пусть мгновенное значение тока имеет вид: i I 2 sin( t ).
u
R L
C
Тогда надо выразить I и через заданные величины.
U
U
U
По первому закону Кирхгофа для действующих значений:
I , I , I .
R R
L x
C x
L
C
I I I I . Построим векторную диаграмму. Из диаграммы следует, что
R L C
I I 2 (I I )2 . Разделим обе части равенства на U .
R L C
U
I
I
Ub
y g 2 (b b )2 , где g, b , b , соответственно,
L C
C x
C
L C
U
U
C
I Ug
R R
проводимости R, L, C. y - полная проводимость
U
I I
y g 2 b 2 , где b b b .
параллельного контура.
L C
L C
U
I
I U y - закон Ома для параллельного контура.
z
U
I Ub
L x
L
L
I I
b b
1
1
1
1
g , b
, b
C, arctg L C arctg L C .
L x
R
L
x
I
g
L
C
R
30.
Треугольники токов и проводимостейТреугольник токов
I I
А R
I
I I I
Р
I
L
C
I
А
Р
- активная составляющая тока,
- реактивная составляющая тока.
I I 2 I 2
А Р
Разделим каждую сторону треугольника токов на U и получим треугольник
проводимостей.
g
y
y g 2 b2 , g y cos , b y sin .
b b b
L C
Пример
I
I 2
I
1
R L
Дано: I 6 А, I 8 А.
1
C
2
Найти I .
I I 2 I 2 I 2 I 2 10 А.
А Р
1 2
31.
Мощности в цепи переменного токаАктивная мощность P
Активной мощностью называется средняя мощность за период T .
1T
P pdt, где p ui. Пусть u U 2 sin t. Тогда ток i I 2 sin( t ).
T0
2UI T
2UI T
P
[cos cos(2 t )]dt UI cos . Таким образом:
sin t sin( t )dt
2T 0
T 0
P UI cos I 2 z cos I 2R U 2 y cos U 2 g. Всегда P 0. P измеряется в Вт.
cos называется коэффициентом мощности.
Реактивная мощность Q
Q UI sin UI IU I 2 z sin I 2 x U 2 y sin U 2b.
Р
Р
Q 0, если 0 (индуктивный характер цепи),
Q 0, если 0 (емкостной характер цепи).
Размерность Q - В А реактивные (ВАр - вары).
Отсюда следует, что
32.
Полная мощностьОбозначается буквой S. S UI ,
S 0 и измеряется в В А (вольтамперы).
Физический смысл S : та наибольшая активная мощность, которая потребляется
электротехническим устройством при наиболее благоприятных условиях работы
(cos 1). Построим векторную диаграмму мощностей:
Q
L
Q
C
i
R
S
Q Q
L C
P
Из векторной диаграммы следует, что S P 2 Q 2 .
Пример
L
C
Дано: I 1 А, R 4 Ом, x 4 Ом, x 1 Ом.
L
C
Найти: Р, Q , Q , Q, S.
L
C
P I 2R 1 4 4 Вт, Q I 2 x 4 ВАр, Q I 2 x 1 ВАр, Q Q Q 3 ВАр,
L
L
C
C
L C
S P 2 Q 2 5 ВА.
33.
ПримерДано: u 50 2 sin( t 20o ),
i 10 2 sin( t 17o).
Найти: R, x, P, Q, S , характер цепи.
U
5 Ом, 370. Характер цепи – индуктивный.
U
I
I
R z cos 4 Ом, x z sin 3 Ом, P UI cos I 2 R 400 Вт, Q UI sin I 2 x 300 ВАр,
L
S UI 500 ВА.
z
34.
Комплексный метод расчёта ЭЦпеременного тока
Метод основан на замене векторов комплексными числами и геометрических
операций над векторами на алгебраические операции над комплексными числами.
Расположим вектор с модулем F и аргументом на комплексной плоскости.
Im( j)
f
2 F
Вектор F
можно представить в трёх формах записи:
F Fe j - показательная форма,
Re( 1) F f f - алгебраическая форма,
1 2
f1
F F cos j F sin - тригонометрическая форма.
f
2
2
2.
F
f
f
,
arctg
Из векторной диаграммы следует:
1
2
f
1
Пусть i I sin( t ).
m
i
j( t )
i I cos( t ) j I sin( t )
I
e
Рассмотрим комплексное число:
m
m
i
m
i
j( t )
i ]. Значит можно ставить в соответствие
Отсюда i Im[ I e
m
j
j
i I - комплексная амплитуда, e j t - множитель
j
t
i I e i e
, где I me
m
m
вращения.
в
р
а
35.
Ij
I - будем обозначать комплекс действующего значения тока. I m , I Ie i .
2
j
j
Аналогично: E Ee e , U Ue u .
Пример
Дано: u 50 2 sin( t 250 ).
Найти: U , U .
m
0
0
j
25
j
25
U 50 2e
, U 50e
.
m
Закон Ома в комплексной форме для резистора
i
R
u
Дано: i I sin( t ). Найти: U, Z R - комплексное сопротивление
m
i
резистора.
i I e j t ; u Ri RI e j t (1). С другой стороны u U sin( t ) U e j t (2).
m
u
m
m
m
Из (1) и (2) RI U . Разделим на 2 и получим: RI U . Отсюда
m
m
U
I
- закон Ома в комплексной форме для резистора.
R
U
Z R - комплексное сопротивление резистора – величина положительная и
R I
вещественная. (Заглавная Z означает комплексное сопротивление, в отличие от
полного сопротивления, обозначаемого z).
36.
Закон Ома в комплексной форме для индуктивностиL
i
L
Дано: iL I Lm sin( t i ), L. Найти: U , Z
L
u
L
- комплексное
сопротивление индуктивности.
L
di
i I e j t , u L
j LI e j t . (1)
Операция дифференциирования в
L Lm
L
Lm
dt
комплексном методе заменяется умножением на j .
С другой стороны
u U sin( t ) U e j t .(2) Сравнивая (1) и (2), получим: j LI U .
Lm
Lm
L
Lm
u
Lm
U
U
U
Lm
Lm
I
Lm j L jx .
- закон Ома для индуктивности. Z
Lm j L
L I
L
Z
L
Lm
Комплексное сопротивление индуктивности – величина мнимая, положительная.
i
C
C
Закон Ома в комплексной форме для ёмкости
U
U Z -комплексное сопротивление
Найти:
i
I
sin(
t
),
C
.
C, C
Дано: C
Cm
i
C
ёмкости.
1T
1
i I e j t , u iC dt
I e j t . (1)
C
Cm
C C0
j C Cm
u U sin( t ) U e j t . (2)
C
Cm
u
Cm
Отсюда:
С другой стороны:
37.
1U
U
I
U , I
- закон Ома в комплексной форме.
Cm
C
1
j C Cm
ZC
j C
U
1
j
1
- комплексное сопротивление ёмкости
Z
Z C
j
jx .
C
C I
C
j C j 2 C
C
C
(величина мнимая, отрицательная).
Последовательный RLC - контур
R C
L
По второму закону Кирхгофа
U
Перейдём к изображениям:
di 1 t
iR L i dt u.
dt C 0
1
1
I R j LI
I U ,U I (R j L
) I Z , где Z R j L 1 .
j C
j C
j C
1
Z R j( L
) R j( x x ) R jx - комплексное сопротивление последовательного
L C
C
RLC контура в алгебраической форме записи. Запишем Z в показательной форме:
x x
jarctg L C
R ze j , - сдвиг по фазе между напряжением и
Z R 2 ( x x )2 e
L C
током.
38.
iu
i i i
R L C
C
R L
Параллельный RLC контур
Определим комплексную проводимость контура Y .
Y
1
1
1 1 1
1
g jbL jbC g j(bL bC ).
Z R Z L ZC R jxL jxC
b b b .
L C
Y g jb, где b – реактивная проводимость контура.
Комплексная проводимость контура в показательной форме:
Y g 2 b 2 e
j arctg
b
g ye j .
Знак «-» - цепь носит индуктивный характер, «+» -
цепь носит емкостной характер.
I U Y -закон Ома для параллельного контура.
Пример. Параллельный контур.
1
3
1
x Ом, x 1 Ом. Найти: Y , характер цепи.
L 5
C
Х
0
а
1
1
1
j
53
g 3 См, b
5 См, b
1 См. Y g рj(b b ) 3 j 4 5e
.
L C
L
С
R
x
x
L
С
а
Дано: R Ом,
Характер цепи – индуктивный.
к
т
е
39.
Пример. Параллельный контур с данными предыдущего примера.0
Дано: u 20 2 sin( t 20 ).
Найти: i.
0
0
0
I U Y Ue j u Y 20e j20 5e j53 100e j33 . Или: i 100 2 sin( t 33o ).
Законы Кирхгофа в комплексной форме
Первый закон Кирхгофа
n
n
i
0
k
I mk 2 sin( t i ). Перейдём к изображениям.
k
k 1
k 1
n
j t
0. Делим на e j t и на 2.
I k e
k 1
n
I k 0 -алгебраическая сумма комплексов действующих значений токов в узле
равна нулю.
k 1
Второй закон Кирхгофа
n
m
n
m
ek uk . Поступая аналогично, получим: Ek U k .
0
0
0
0
40.
ПримерE
Дано: i 2 2 sin( t 250 ), R 3 Ом, x 2 Ом, x 6 Ом. Найти e.
C
R C
L
L
I
0
0
0 j530
0
j
25
j
25
j
25
j
78
E IR Ijx Ijx I [ R j( x x )] 2e
(3 j 4) 2e
(3 j 4) 2e
5e
10e
.
L
C
L C
Мгновенное значение ЭДС: e 10 2 sin( t 780 ).
Комплексная мощность
j
Умножим комплекс напряжения U на сопряжённый комплекс тока I Ie
i
и обозначим полученный комплекс через S .
j( )
S U I UIe u i UIe j UI cos j sin P jQ.
Таким образом, активная мощность P – действительная часть, а реактивная
мощность Q - мнимая часть комплексной мощности.
Q 0
- цепь имеет индуктивный характер, Q 0 - цепь имеет емкостной характер.
41.
Эквивалентные параметры пассивных двухполюсниковПусть имеются два двухполюсника с параллельной и последовательной цепями.
1
Z
1 Y
1
g
b
1
Z
2 Y
2
R
x
Задача: имея параллельную цепь, заменить её последовательной и наоборот.
Z , Z - входные комплексные сопротивления, Y ,Y -входные комплексные
1 2
1 2
проводимости. Приравняем их, тогда двухполюсники будут эквивалентны.
1
1
g jb
g
b
Z
j
Z R jx. Тогда, переход от параллель1 Y g jb
2
g 2 b 2 g 2 b 2
g 2 b 2
1
g
g
b
b
ного соединения к последовательному: R
2, x
2.
g 2 b 2 y
g 2 b 2 y
1
1
R jx
R
x
Y
j
Y g jb. Переход от последователь2 Z
1
2
2
2
2
2
2
R jx R x
R x
R x
2
R
R
x
x
ного соединения к параллельному:
g
2 , b
2.
R2 x2 z
R2 x2 z
42.
Последовательное соединение комплексных сопротивленийZ
1
Z
2
U
Z
I
n
n
U U I Z (1).
k
k
k 1
k 1
n
Из (1) и (2): Z Z .
k
Э
k 1
Z
n
U
I
U I Z (2).
Э
Каждое комплексное сопротивление может содержать
активную и реактивную составляющие: Z R x .
n
m
l
Z Z R j x .
k
k
k
Э
k 1
k 1
k 1
Пример
R1
x
x
C1 L
Э
k
k
Дано: R1 1 Ом, x
x
R2 C 2
C1
k
Тогда
10 Ом, x 8 Ом, R2 2 Ом, x 2 Ом.
L
C2
Найти: Z .
0
Z R1 R2 j( xL xC1 xC 2 ) 3 j(8 12) 3 j 4 5e j53 .
43.
Параллельное соединение комплексных сопротивленийI
I
I
1
2
Y1 Y 2
U
Y
n
I
n
n
По первому закону Кирхгофа: I I ,
k
U
I
I U Y .
k
k
Y
Э
Подставив I
k 1
n
U Y I (1). В эквивалентной схеме замещения I U YЭ (2).
k
k 1
l
n
n
m
n
Y Y g j b
U Y UY , Y Y .
k
k
k
k
Э
k Э
Э
1
k
1
1
1
k 1
k
Приравняем (1) и (2)
Пример
g
g
1
2 b
b
C
1
L
Y g g j(b b b ).
1 2
L C1 C 2
b
C2
, получим
44.
I1
R1
U
jx
L
U
Смешанное соединение
a
I
2
I
3 U
ab U
R2
R
L
Э
jx
C b
Z R1 jx , Z jx , Z R2.
1
L
2
C
3
R x2
R2 x
Z Z Z R1 2 C j( xL 2 C ) RЭ jxЭ.
Э 1 23
R 2 x2
R 2 x2
2
C
2
C
U
R1
x
Э
Выводы:
1. Эквивалентные параметры R и x сложным образом зависят от параметров элементов
Э
Э
и частоты.
2
R x
2 C
x
(
)
2. Если L
R2 x2
2 C
U
U
I
2 U
L
-характер цепи – индуктивный (емкостной).
Построим векторную диаграмму.
R1
U
L
R1
I
1
I
3
U
U
ab
Здесь характер цепи – емкостной,
так как 0.
45.
Методы составления мат. моделей процессов в ЭЦСоставление мат. модели с помощью уравнений Кирхгофа
Система интегродифференциальных или алгебраических уравнений, описывающая
переходные или установившиеся процессы, называется математической моделью.
i
1
e (t)
1
1
i
4
R
1
2
i
R
3
2 II
I
i
C
5
L III 3 R
5
j(t )
i
2
4
Обозначим узлы и контуры.
Выберем направление обхода контуров.
Пусть n – число токов и уравнений, q –
число узлов.
n q 1 - число уравнений по первому
1
R
закону Кирхгофа, n n n - число уравнений
i
e (t)
6
2
1
6
6
по
второму
закону
Кирхгофа.
1 узел i i i 0, (1)
6 4 1
В нашем случае:
2 узел i i i j(t), (2)
1 2 3
n 6, q 4. n 4 1 3, n 6 3 3.
3 узел i i i 0, (3)
1
2
3 4 5
di
1t
I контур i R i dt L 4 e (t ), (4)
11 C 3
dt 1
0
1t
II контур i R i R i dt 0, (5)
2 2 5 5 C 3
0
di
III контур L 4 i R i R e (t ). (6) Полученная система уравнений называется
6
математической моделью.
dt 5 5 6 6
46.
Частный случай. Пусть воздействие – синусоидальное. Тогда можно записатьуравнения (1) –(6) в комплексной форме:
I I I 0,
6 1 4
I I I J ,
1 3 2
I I I 0,
3 5 4
1
I R
I j LI E ,
1 1 j C 3
4 1
1
I R I R
I 0,
2 2 5 5 j C 3
j LI I R I R E .
4 5 5 6 6
6
I , I , I , I , I , I . i , i , i , i , i , i .
1 2 3 4 5 6
1 2 3 4 5 6
47.
Метод расчёта цепей, основанный на принципе наложенияМгновенное значение тока в любой ветви сколь угодно сложной ЭЦ равно
алгебраической сумме мгновенных значений токов в этой ветви, создаваемых
каждым источником в отдельности.
Порядок расчёта.
1. Исключаем все источники, кроме одного. При этом, заменяем источники ЭДС
их внутренними сопротивлениями, а источники тока их внутренними проводимостями.
Рассчитываем цепь и определяем i1, i1 , i1 .
1 2
n
2. Оставляем в цепи другой источник, исключая все остальные и повторяем
2 2
1 2
2
n
расчёт, определяя i , i , i .
3. Осуществляем наложение
Пример
E
I R
1 1
Дано: R , R , R , J , E, R 0, g 0. Найти: I .
1 2 3
J
R R
2 3
m (k )
m (k )
i i , где m – число источников, i i .
1
2
1
2
k 1
k 1
0
0
1
48.
EI1 R
1 1
R R
2 3
a
I2
1
R
1
1. Исключим источник тока. Остаётся цепь:
I1
1
E
.
R2 R3
R1
R2 R3
2. Исключим источник ЭДС.
J
b R R
2 3
U
R R
R1R2 R3
2
ab
2 3
J
.
U J
, I
1
ab
R
R
R
R
R
R
R
R1R2 R1R3 R2 R3
1
1 2 2 3 1 3
3. Осуществим наложение:
I I1 I 2 (но не наоборот).
1 1 1
Замечания по исключению источников
Реальный источник ЭДС
E
R
0
Идеальный источник ЭДС E
Реальный источник тока
J
g
Идеальный источник тока J
0
R
0
Короткое замыкание.
g0
Холостой ход.
49.
Метод контурных токов (метод Максвелла)Недостаток метода уравнений Кирхгофа – большое число исходных уравнений.
Метод контурных токов позволяет значительно сократить число уравнений.
Полагают, что в каждом контуре течёт свой контурный ток. Уравнения составляют
относительно контурных токов, затем определяют токи в ветвях.
Пусть цепь содержит n контуров. Выделим из неё один контур и назовём его первым.
I
2
3
I
k3
I
1 Z Z2
Z
3
1 1
2
I
I
E
k1
k2
E
2
1
I
n 1 n I kn
Направление токов выбираем произвольно. Предположим, что
В каждом контуре протекает фиктивный контурный ток I , I ,…
I . По второму закону Кирхгофа для 1 контура:
kn
E E I Z I Z I Z . ( )
1 3 1 1 2 2
n 1 n 1
k1
k2
Действительные токи:
I I I ,
1 k1 k 2
I I I ,
2 k1 k 3
(1)
……………..
I
I I ,
n 1 kn k1
Подставим (1) в ( ) и обозначим:
Z Z Z Z
11 1 2
n 1 - собственное сопротивление 1-го контура, Z12 Z1 - взаимное
сопротивление между 1 и 2 контурами, Z Z - взаимное сопротивление между 1 и 3
13 2
Z
Z
контурами, 1n
n 1 - взаимное сопротивление между 1 и n контурами.
50.
Взаимные сопротивления берутся со знаком (+) если контурные токи протекают черезних в одном направлении и со знаком (-), если – в противоположном.
Для всех n – контуров система уравнений (математическая модель) имеет вид:
I Z I Z I Z E 1 E 3 E k1,
k1 11 k 2 12
kn 1n
I Z I Z I Z E k 2 ,
k1 21 k 2 22
kn 2n
(2)
…………………………………………
I Z I Z I Z E kn.
k1 n1 k 2 n2
kn nn
Число уравнений сокращается на величину n q 1.Число неизвестных в этом методе
1
равно числу уравнений, составленных по второму закону Кирхгофа, следовательно,
этот метод более экономичен, чем метод на основе законов Кирхгофа.
Порядок расчёта.
1. Составляется система уравнений (2).
2. Решается система уравнений относительно I .
k
3. По уравнениям (1) определяются действительные токи.
I
1
E
1
R
1
Пример
I
R
2
2
x
I
x
L1
3
L2
I
E
I
2 k2
k1
x
C
I [R j( x x )] I [ ( jx )] E E ,
k1 1
L1 C
k2
C
1 2
I [ ( jx )] I [R2 j( xL2 xC )] E .
k1
C
k2
2
Отсюда получим I , I :
k1 k 2
I I , I I , I I I .
1 k1
2 k2
3 k1 k 2
51.
Метод эквивалентного генератораМетод применяется, когда надо определить ток в какой – либо одной ветви сложной ЭЦ.
Теорема Тевенена. По отношению к выделенной ветви a b, оставшееся часть сложной
ЭЦ, содержащей источники ЭДС и тока, может быть заменена эквивалентным генератором
с ЭДС E и внутренним сопротивлением Z . .
E
Г
a
I
н
Z
н
Г
Z
E
Г
Г
b
a
Г
Z
Г
I E Г .
н Z Z
Г н
Здесь неизвестны E
Г
и Z .
Г
1. Определим E . Используем режим холостого хода (ХХ). (Ветвь
Г
с нагрузкой разрываем).
I 0, U E . E - определяется экспериментально, как напряжение
н
хх
Г Г
в режиме холостого хода.
b
2. Определим Z . Z
Г
Г
- представляет собой входное сопротивление
активного двухполюсника. Для его определения надо: а) источники ЭДС заменить их
внутренними сопротивлениями; б) источники тока – внутренними проводимостями;
в) рассчитать сопротивление на зажимах a и b.
52.
Осуществим режим КЗ.E
Z
Г
Г
a
U
U
I E Г хх , Z хх .
КЗ Z
Г I
Z
Г
Г
КЗ
I
КЗ
b
Пример. Определение параметров эквивалентного генератора.
a
Акт.
двухп.
b
V
R 40 Ом.
н
А
Найти I н.
Подключим поочерёдно вольтметр и амперметр к активному двухполюснику. Показания
приборов: U 20 В, I 0,5 А (R , ХХ ) (RА 0, КЗ).
1. E
Г
U
2. I I
хх
U 20 В.
V
0,5 А.
кз
E
U
3. R Г 40 Ом.
Г I
I
кз
EГ
20
I
0,25 А.
4. н
RГ Rн 40 40
53.
Примерx
I
C
x
C
R
L
b
E
I ХХ
x
a
R
L
E
Дано: xL =10 Ом, xC =5 Ом,
R =10 Ом,
0
j
60
E 100 2e
. Найти: iC .
1. Выделяем ветвь с нагрузкой и осуществляем режим ХХ.
Оставшуюся часть считаем ЭГ.
2. Найдём U
.
ХХ
a
U
j600
j600
0
E
100 2e
100 2e
j
15
U
U , I
10e
ХХ
R
ХХ R j L
0
10 j10
j 45
ХХ
10 2e
0
j
15
EГ U
I
R 100e
.
b
ХХ
ХХ
3. Найдём Z Г (входное сопротивление относительно зажимов a, b).
j900
R jx
10 j10 100e
10 j 450 10 2
10 2
L
Z
e
j
5 j5.
Г R jx 10 j10
0
j 45
2
2 2
2 2
L
10 2e
4.Определим I
C
- ток нагрузки.
E
j150
Г 100e
I
. i 20 2 sin( t 150 ).
C Z Z
C
5 j 5 j 5
Г Н
54.
Резонансные явления в электрических цепяхОсновные понятия о резонансе
I
U
R,
L,
В общем случае 0.
Режимы, при которых ток и напряжение совпадают по фазе
( 0) называются резонансными.
C
Последовательный резонанс (напряжений)
z R 2 ( x x )2 ,
L C
x x
tg L C ,
R
0, x x 0,
L C
т. е. x x
L0 C0
- условие последовательного резонанса.
z R.
0
Параллельный резонанс (токов)
y g 2 (b b )2 ,
L C
b b
tg L C ,
g
0, b b 0,
L C
т. е. b b
L0 C 0
- условие параллельного резонанса.
y g.
0
55.
Резонанс при последовательном соединении R, L, C.U
I
Резонанс напряжений.
R
R
U
L
C
U
C
x x - условие резонанса.
L C
U L 1 , 2LC 1. При L, C const, 1 ,
L
0
C
LC
1
, C const, L 12 , , L const, C 2 .
0 L
0 C
- собственная частота контура.
0
Приложенное напряжение:
U
R0
U
U Iz I z I R U R0.
00 0
- напряжение, приложенное к резистору при резонансе.
Строим векторную диаграмму.
U
L0
I x
0 L0
U
I
0 R
U I R U
R0 0
U
C0
I x
0 C0
Из диаграммы следует, что всё приложенное
напряжение оказывается на резисторе.
56.
Добротность. Волновое сопротивление.U U
, но U U 0.
C0
L0
1
L
L
U
I x
L
L0 0 L0 0 LC C Q.
U
I R
R
R
R R
0
R0
1
L
U
I x
C 0 0 C 0 0C LC C Q.
U
I R
R
RC
R R
0
L -волновое сопротивление контура. Оно равно сопротивлению реактивного элеC
Q
мента на резонансной частоте.
- добротность контура. Она показывает, во сколько раз напряжение на реактив-
R -ном элементе при резонансе больше приложенного.
1
d - затухание контура.
Q
U - напряжение на L и C при резонансе.
U U QU
L0
C0
d
57.
Частотные характеристики последовательного контураЭто изменение R, x , x , x, в зависимости от частоты.
L C
R, x , x , x,
L C
z
x
x
R
0
Емк. хар.
x
C
1
C ,
R
L
- резонансная частота.
0
2
2
R const,
x L,
C
1
x
,
C C
z R2 x2 ,
arctg
Индуктивный характер
L
При 0, tg , .
2
При , tg , .
2
58.
Резонансная кривая токаI ( )
)
F
(
Обозначим:
- относительное изменение тока. Эта резонансная кривая
I ( )
0
0
- относительную частоту.
тока. Построим её. Введём также
0
U
U
, I ( ) . Тогда
0 R
z
z R 2 ( x x )2 .
L C
I ( )
I ( ) U U R
, где R const (не зависит от частоты),
z
R
z
I ( )
0
0 L
L
L
x
L
,
Выразим реактивные сопротивления через . L
0
LC
C
1
1 LC
x
0
.
Относительное изменение тока:
C C C C
0
R
R
R
1
1
F ( )
.
z
1
1
1
1 2
R 2 ( )2
R 2 2 ( )2
1 ( )2
d2
1
d
1
.
Т. е. уравнение резонансной кривой: F ( )
1 2
1
d
59.
Определим частоты, при которых F ( ) 1 . Для этого решим уравнение:2
1
1
1
[1 ( )2 ] 2 .
Возведём в степень (-2).
d
2
1
1
1
1
1,
d , 1 d 0, 2 d 1 0.
2 1 ( )2, ( )2 1,
d
d
d
d
d2
d
2
1,
1 случай: d 1 0.
2 2
4
- т. к. 0.
2
d2
d
2
1, -т. к. 1 0.
2 случай: d 1 0.
1
4
0
2
.
1.
Получили 2 1 Видно, что d. Резонанс в относительных частотах: 0
0
2 1
F ( )
1
1
Так как d , то чем больше Q , тем уже F ( ) , тем лучше
1
Q
d
избирательные свойства контура.
2
I 1
Условно считается, если
0,707 - контур пропускает и
1
I
2
1
0 2
I
1
0,707.
наоборот. В полосе пропускания
I
2
0
0
S
d
.
Полоса пропускания в абсолютных частотах:
2 0 1 0 0
Q
60.
Резонанс при параллельном соединении R, L, CI
U
I
I I
R L C
C
R L
Резонанс токов
b b
1
1 - резонансная
tg L C 0, т. е. b b
или
C
L0 C 0
0 LC
g
L
2
2
частота. При этом, y g (bL bC ) min g.
Строим векторную диаграмму.
I U b
C0
C0
Входной ток I при резонансе равен току через резистор I .
I U g
R0
R0
U
I
L0
U b
L0
Рассмотрим отношение токов:
1
C
LC
I
U b
L
L0
L0 0 L L Q.
I
U g
g
g
g
g
R
Здесь
C
L
- волновая проводимость, т. е.
проводимость реактивных элементов на резонансной частоте.
C
I
U b
C0
C 0 0C L Q. Q - добротность, показывает во сколько раз ток через
I
U g
g
g
g
R
реактивный элемент больше входного тока I .
61.
Частотные характеристики параллельного контураЭто изменение g , bL , bC , b, y,
в зависимости от частоты.
g , b , b , b, y,
L C
1
b ,
L L
y
g
b
L
b
Инд. х-р
Емк. х-р
b C,
C
b b b ,
L C
y b b ,
L C
b
C
2
2
b b
C.
g
arctg L
62.
Расчет ЭЦ при наличии взаимной индуктивностиЗакон электромагнитной индукции
i
w
L
Определение: магнитный поток, создаваемый током в контуре и
сцепляющийся с этим контуром называется потоком самоиндукции.
[ ] - Вб (Вебер), w - число витков. Потокосцепление самоиндукции
L
в контуре в w раз больше, чем
Из опытов известно:
катушки. Размерность L - Гн (Генри).
Li,
L
L
где
: L w L .
L - собственная индуктивность
Пусть поток изменяется во времени. Тогда i(t ) (t ) e(t ) и возникает ЭДС
L
самоиндукции.
Закон электромагнитной индукции
В замкнутом контуре индуцируется ЭДС, пропорциональная скорости изменения
магнитного потока, пронизывающего поверхность, ограниченную контуром, взятая
со знаком «-». При изменении L наводится ЭДС самоиндукции e :
d
L.
e
L
dt
di
e L .
L
dt
Тогда E j LI .
L
Предположим, что L const, тогда
Пусть ток – синусоидальный: i I sin t.
m
L
63.
Рассмотрим два контура с током.i
1
i
2
M
- поток взаимной индукции. Потокосцепление второго
контура: M M w2.
С другой стороны: M Mi1, где
M
w
2
M - взаимная индуктивность 2-х контуров (зависит от геометw
1
рических размеров и взаимного расположения катушек). M - в Гн.
Переменный ток i создаёт переменное потокосцепление , и во втором контуре
1
наводится ЭДС взаимной индукции eM
При M const,
d
M
M.
dt
di
e M 1 . При синусоидальном токе: E j MI .
M
M
1
dt
Введём k - коэффициент, характеризующий степень связи между катушками. k
k 1, если не будет потока рассеяния, но на практике он всегда есть.
M
.
LL
1 2
64.
Согласное и встречное включение индуктивно связанных катушекi
1
L
1
i L
2 2
M
di
e M 2
1M
dt
di
e
M 1
2M
dt
1
1L
M
.
Знак
говорит о том, что
основной поток может усиливаться или ослабляться потоком взаимной индукции.
«+» – согласное включение (поток усиливается).
«-» – встречное включение (поток ослабляется).
L I Mi .
1
11
2
При расчёте цепей будем учитывать eM в явном виде, т. е. в виде источников ЭДС,
di
e
M
.
направление которых совпадает с направлением тока, а величины их равны: M
dt
или - начало катушки.
Включение считаем согласным, если токи в обеих катушках протекают в одном направлении по одноименным зажимам, а встречное – по разным. На схеме изображено
встречное включение.
65.
Последовательное включение индуктивно связанных катушекR
1
I
E
( j MI ) R
1M
2
L
1
E
( j MI )
2M
L
2
M
U
U
1
U
2
Напряжения на первой и второй индуктивностях: U I R I j L j MI ,
1
1
1
U IR Ij L j MI . «+» - при согласном включении, «-» – при встречном.
2
2
2
Входное напряжение: U U U I ( R R ) I j ( L L 2M ).
1
2
1
2
1
2
Можно использовать схему замещения двухполюсника:
R
экв
R R1 R2, L L L 2M .
экв
экв
L
экв
Обозначим: Z R j L ,
1
1
взаимной индукции.
Z
встр
Z
.
согл
чения катушек.
Пример.
U
1
- сопротивление
Z R j L , Z 2 j M , Z
2 2
2
M
M
Это обстоятельство используется при определении характера вклю-
вх
100 В, I1 5 А.
Тогда Z 20 Ом.
катушек поменяем местами. Повторим: U
Теперь зажимы одной из
1
100 В, I2 10 А. Тогда Z 10 Ом.
вх
2
Значит, в первом случае, было согласное включение.
66.
Векторные диаграммыСтроим при условии: L M L .
I j M
U
1
Согласное включение
U 2 I j L2
, , 0.
2
I R
2
I j M
U1
1
I j L
1
IR
1
1 2
I
I j L I j M
2
I j L
1
U
U 2
I R
2
1 U
1
1
I j M I R
2
2
Встречное включение. Явление ложной ёмкости.
Строим при условии:
I
L M L .
1
2
1 0 !!! Первая катушка ведёт себя как ёмкость.
Это явление называется ложной ёмкостью и наблюдается, если L M .
1
67.
Параллельное включение индуктивно связанных катушекI
U
I
1
R
1
1 L
1
R
2
M
2
L
2
I
2
U
Дано:R , L , R , L , M .GG Найти: Z .
I
1 1 2 2
По 1-му закону Кирхгофа:
I I I ; (1)
1 2
По 2-му закону Кирхгофа для 1-го и 2-го контуров:
U I R j L I j MI I Z I Z ; (2)
11
11
2 1 1 2 M
U I R j L I j MI I Z I Z . (3)
2 2
22
1 1 M 2 2
E j MI E
j MI
1M
2 2M
1
Определим токи I и I .
1
2
1 Z
Z1 1
M
I
Z Z
I
1
Z
Z
Z
ZM 1
I U 1 U
2 U 2 M ;
I U 2 U
U 1 M ;
2
Z
Z
1
Z
Z
Z Z Z 2
1
M
Z Z Z 2
1
M
1 2 M
1 2 M
Z
Z
Z
Z
M
2
M
2
2
Z
Z
Z
Z
Z
2
Z
U
M.
Входной ток: I I I U 1 2
Отсюда: Z
1 2 M ;
2
1 2
согл I Z Z 2Z
Z1Z 2 Z M
1 2
M
Z Z Z 2
U
L L M 2
Z
.
Z
1 2 M ; Z
согл встр Если R R 0, L 1 2
встр I Z Z 2Z
.
1 2
Э L L 2M
1 2
M
1 2
68.
Трансформатор без ферромагнитного сердечникаВоздушный трансформатор
I
1
U
1
I
2
R
1
L
1
R
2
M
U
L 2
2
Z
Н
Принцип действия
Z
Первичная обмотка
Н
R jx
Н
Н
U
1
I
1
I R
1 1
j L I
11
E
j MI
1M
2
Вторичная обмотка
E
j MI
2M
1
U
2
I
I R
2
2 2
j L I
22
Уравнения трансформатора:
U I R j L I j MI ,
1 11
11
2
j MI I R j L I U , где U I (R jx ).
1 2 2
22 2
2 2 Н
Н
(согл. включ.)
69.
Т – образная схема замещения воздушного трансформатораЗапишем уравнения трансформатора в следующем виде:
U I R j L I j MI ,
1 11
11
2
0 I R j L I j MI U .
2 2
22
1 2
К 1-му уравнению прибавим и отнимем j MI :
1
U I R I R j MI j MI j MI I R j I (L1 M ) j M (I 1 I 2 ).
1 11 11
2
1
1 11
1
Ко 2-му уравнению прибавим и отнимем j MI :
2
0 I R j L I j MI j MI j MI I R j I (L2 M ) j M (I 1 I 2 ) U .
2 2
22
1
2
2 2 2
2
2
R
L M
L M R
I
I
1
1
2
2
1
2
U
I I I .
U
M
1
3 1 2
2
I
3
(или L )
L M L
1
1d
1S
L M L
2
2d (или L2S )
Индуктивности рассеивания первичной и
вторичной обмоток.
70.
Трёхфазные цепи и методы их расчётаПонятие о многофазной системе электрической цепи
N
C
A
S
120 0
ЭДС, наводимые в обмотках, будут одинаковы и сдвинуты относительно друг друга на 1/3 периода. Если генератор имеет m фаз, то
ЭДС сдвинуты на 2 m.
Для трёхфазной цепи:
B
Векторная диаграмма
E
E
C
A
1200
E
A
E
B IA
a
Z
E
I
C
Совокупность нескольких цепей, в которых действуют синусоидальные ЭДС, отличающиеся друг от друга начальной фазой, называется многофазной системой электрической цепи.
A
E
C
C
2
4
e E sin t, e E sin( t ), e E sin( t ).
A m
B m
C
m
3
3
B
B
Z
C
I
B
a
U
a
Z
U U
C C b
b
b
Здесь фазой называется участок цепи, по
которому течёт одинаковый ток.
Линейные провода соединяют генератор и
нагрузку.
Совокупность E, U, I называется многофазной системой E, U, I.
71.
Если Z Z Z , то нагрузка называется симметричной. Если z z z , тоа
b
а
c
нагрузка называется равномерной.
Пример равномерной нагрузки: Z 10 Ом,
a
b
c
0
0
j
30
j
30
Z 10e
Ом, Z 10e
Ом.
b
c
Симметричные многофазные системы E, U, I
Многофазная система E (U, I) является симметричной, если все действующие значения
одинаковы, и если каждая последующая E (U, I) отстаёт от предыдущей на угол 2 m.
E
1
E
3
2
8
E
2
Несимметричная система
Симметричная 8-ми фазная система
Теорема 1. Сумма мгновенных значений e, u, i в симметричной системе равна нулю.
m
m
Или
в
комплексной
форме:
E n 0.
en 0.
n 1
n 1
Для трёхфазной системы: E E E 0, I I I 0.
A B C
a b c
Теорем 2. Если симметричны система ЭДС и нагрузка, то симметрична и система токов.
E
A
I I a
c
E
C
I E
b
B
0
j
Z ze
, 0.
72.
IA
E
O
E
C
I
C
C
Способы связывания трёхфазных цепей
Соединение звездой
a
A
Z
I
0
A
E
B
B
Z
c
a
U
a
O1
U U
c
c b
U
AB O O1 - нулевой провод,
Aa, Bb, Cc - линейные провода,
- линейные токи,
I
Z
A
,
B
,
C
b
b U a,b,c - фазные напряжения,
- линейные напряжения.
I
U
B
AB, BC,CA
Для «звезды»: I
I . По 1-му закону Кирхгофа: I I I I .
фазн лин
0 A B C
Для симметричной трёхфазной цепи: I 0.
0
Составим уравнения по 2-му закону Кирхгофа для контура a b O :
1
U U
U 0. Отсюда:
a
AB b
U
U U .
AB
b a
Аналогично:
U
U U ,
BC
c b
U U U .
CA
a c
73.
UU
U
c
Из треугольника U U O :
a
300
U
ab
ca
O
1
U
bc
a b 1
U
U
лин
2U
фазн
cos300 2U
3
3U
, U
3U
.
фазн 2
фазн
лин
фазн
b
фазн 220 В.
При линейном напряжении 220 В U фазн 127 В.
Рассчитаем активную мощность: P U I cos U I cos U I cos .
a a
a bb
b cc
c
При линейном напряжении 380 В U
Симметричный случай:
U
P 3U
I
cos
3 лин I
cos
3U
I
cos
.
фазн фазн
фазн
лин
фазн
лин
лин
фазн
3
Реактивная мощность в симметричном случае:
U
Q 3U
I
sin
3 лин I
sin
3U
I
sin
.
фазн фазн
фазн
лин
фазн
лин
лин
фазн
3
74.
Соединение треугольникомI a
A
E
O
E
C
C
A
a
U
Z ca
I
ca
B c
I c
U
I b
По 1-му закону Кирхгофа:
I
ф
ca
U
bc
Здесь U
I
ab
лин
U
фазн
.
Z ab
ab
I
bc
b
Z bc
I I I ,
a ca ab
I I I ,
b ab bc
I I I .
c bc ca
300
I
I
ф
л
O
1
I
л
U
P 3U
I
cos
3 лин I
cos
3U
I
cos
.
фазн фазн
фазн
лин
фазн
лин
лин
фазн
3
I
л
I
ф
75.
Нелинейные токи и напряженияЛюбую периодическую функцию (e, u, i) можно разложить в ряд Фурье:
e(t) E E sin( t ) E sin( 2 t ) E sin( n t ) .
0 1
1
2
2
k
k
Токи от действия ЭДС определяются методом наложения.
Пример
i(t )
Дано:R 4 Ом, x 3 Ом, u(t ) 5 10sin t 2sin 3 t. Найти: i, P.
R
L
u(t )
1. k 0. Постоянная составляющая.
U
5
2
2
U 5 В, x 0, z R x
4 Ом, I 0 1,25 А.
L0
0
L0
0
0 z
4
0
2. k 1.
U
U 10 В, x 3, z R 2 x 2 16 9 5 Ом, I m1 2 А, i1 2sin( t 370 ),
L1
m1
L1
1
m1 z
1
3. k 3.
L
U
x
2 В, x kxL1 9 Ом, z R 2 x 2 9,8 Ом, I m3 0,2 А, 3 arctg L3 73,40.
L3
m3
L3
3
m3 z
R
3
i 0,2sin(3 t 73,40).
3
2 ( I1m )2 ( I3m )2 1,893 А,
0
0
I
I
i I i i 1,25 2 sin( t 37 ) 0,2 sin(3 t 73,4 ).
0
0 1 1
2
2
2
P I R 14,33 Вт.
U
76.
Переходные процессы в электрических цепяхПостановка задачи расчёта переходных процессов
Дано: 1. Схема и параметры элементов цепи. 2. Вид коммутации. 3. Начальные условия.
Найти: i(t ), u (t ) после коммутации.
Порядок расчёта переходных процессов
1).Составить систему уравнений для i(t ), u (t ) после коммутации и записать
уравнения связи.
n
n 1
d i
d
i
di
a
a
a i f (t ) (1).
n 1 n 1
1
0
n
dt
dt
dt
n nL n , где n - число индуктивностей, n , - число ёмкостей,
n - порядок уравнения.
C
L
C
n
pn 1 a p a 0 и найти корни
3). Записать характеристическое уравнение: p a
n 1
1
0
p , p , p .
1 2
n
4). Ищется решение уравнения (1) в виде: i i i , где iпр- принуждённый ток
пр св
(определяется как установившееся значение i при t ), i - свободный ток:
св
p t
pt
p t
i A e 1 A e 2 A e n , где A1, A2, An - постоянные интегрирования.
св 1
2
n
n
p t
k и определяем A , A , A по известным начальным
i
i
A
e
5). Записываем:
пр
k
1 2
n
k 1
2). Решить эту систему относительно iL (t ), uC (t ).
условиям и законам коммутации.
77.
6). Определяем остальные токи в ветвях и напряжения на участках цепи из уравненийсистемы.
Законы коммутации
L
Первый закон коммутации
i
L
Пусть индуктивность с током iL имеет потокосцепление L.
Предположим, что L изменяется по закону, приведенному на рисунке,
то есть при t t0 потокосцепление претерпевает скачек.
L
Тогда ЭДС самоиндукции на катушке при t t ,
L
t
t
0
0
d
L , стремится к бесконечно большой величине,
e
L
dt
что физически невозможно.
Первый закон коммутации. Потокосцепление индуктивности непосредственно до
коммутации равно потокосцеплению сразу после коммутации.
(0) (0 ).
Если индуктивность в результате коммутации не меняется, то первый закон коммутации
можно записать для токов: так как Li , то i (0) i (0 ) при L const.
L
L
Следствие 1-го закона: ток до коммутации равен току сразу после коммутации.
t 0 R
Пример. Индуктивность в результате коммутации не изменилась.
Тогда i(0 ) i(0) 0. Какую бы ЭДС по величине не включать, ток в
E
L
i
в первый момент после коммутации равен нулю и начинает нарастать
от нуля.
78.
Пример. В результате размыкания ключа, индуктивность изменилась,была L , стала L L . Поэтому, для определения i(0) восполь1
1 2
зуемся основной
формулировкой
1-го закона коммутации:
R
E
E
(0 ) L1i(0 ) L1 , (0) (L1 L1)i(0), но (0) (0 ).
L
R
L
2
1 i(0 ),
i
(
0
)
Следовательно, L i(0 ) (L L )i(0), откуда
1
1 2
L L
1
2
т. е. i(0) i(0 ). Ток изменился скачком.
t 0
Энергия магнитного поля в катушке L до коммутации
i
1
2 (0 )
L
i
i(0 )
, после коммутации энергия запасается в
W (0 ) 1
i(0)
t М
2
L
1
индуктивностях L L , следовательно:
1
2
L L2 2
L L2 L1 2 2
L L1 2
L
W (0) 1
i (0) 1
(
) i (0 ) 1
i (0 ) 1 W (0 )
М
2
2
L1 L2
L1 L2 2
L1 L2 М
и энергия сразу после коммутации уменьшается скачком. На самом деле при размыкании
ключа между его контактами возникает электрическая дуга и в ней происходит за очень
короткое время выделение энергии, равное W (0 ) W (0).
М
М
79.
Второй закон коммутацииu
C
q
Пусть ёмкость с током iC имеет заряд q . Предположим, что заряд
q изменяется по закону, изображённому на рисунке, т. е. при t t
0
заряд изменяется скачком. Тогда ток:
i
C
C
t
0
dq
i
стремится к бесконечности, что невозможно.
C (t ) dt (t )
0
0
Поэтому скачкообразных изменений заряда q не может быть.
t
Второй закон коммутации. Заряд ёмкости сразу после коммутации
равен её заряду до коммутации: q(0) q(0 ).
Но q CuC , и, если ёмкость C в результате коммутации не изменяется, то можно записать
следствие второго закона коммутации для напряжений в виде: uC (0) uC (0 ).
E
R
t 0
Пример. Ёмкость в цепи при коммутации не меняется, поэтому:
C
u
C
u (0 ) u (0) 0.
C
C
Какую бы по величине ЭДС мы не включали, если конденсатор не был
предварительно заряжен, то напряжение на нём начинает изменяться от нуля.
E
R t 0
Пример. В результате коммутации ёмкость изменилась,
C2
C1
u была C1 , стала C1 C2 . Поэтому для определения uC (0)
C
применим основную формулировку 2-го закона коммутации.
q(0 ) C u (0 ) C E, q(0) (C C ) u (0), но q(0 ) q(0), следовательно
1C
1
1 2 C
C
1 u (0 ), т. е. u (0) u (0 )
u
(
0
)
C u (0 ) (C C ) u (0), откуда
C
C
C
1C
1 2 C
C C C
1 2
и это изменение происходит скачком.
80.
uC
u (0 )
u (0)
C
C
t
На самом деле эти изменения не происходят мгновенно. При
подключении C 2 в ключе проскочит искра и энергия, практически
мгновенно, но всё же за конечное время, выделится в виде тепла.
Пример. Для цепи на рис. определить uC (0).
R1
U
t 0
В соответствии с законом коммутации uC (0 ) uC (0),
R2
UR
2 .
u (0 ) iR R
2 2 R R
C
1 2
UR
2 .
u (0)
C
R R
1 2
C
но
i
L
Пример. Для цепи на рис. определить iL (0).
Следовательно:
t 0
U
R1
R2
L
U
i
(
0
)
.
До коммутации в цепи протекал ток: L
R
1
В соответствии с законом коммутации:
U
i (0) i (0 ) .
L
L R
1
81.
Переходные процессы в цепях с индуктивностью при постоянномвоздействии
Замыкание цепи RL накоротко
R
Дано: U, R, L. При t=0 цепь R, L замыкается накоротко.
t 0
U
R
u u
R L
i
L
L
Найти: i(t ), u (t ), u (t ).
R
L
Ниже на рис. приведена цепь после коммутации. Выберем
положительные направления тока i и напряжений u , u ,
R L
как показано на рисунке.
По 2-му закону Кирхгофа: uR uL 0.
.
di
u
iR
,
u
L
.
Уравнения связи: R
L
dt
di
iR 0. Характеристическое уравнение: Lp R 0.
dt
R
Корень характеристического уравнения: p .
L
pt
Свободная составляющая тока: i A e .
св
Принуждённая составляющая тока: iпр 0.
Полный ток: i i i Ae pt .
св пр
Дифференциальное уравнение: L
82.
Для определения начального условияU
i(0) , изобразим цепь до коммутации.
U
U
Ток до коммутации: i(0 ) . По закону коммутации:i(0) i(0 ) .
R
R
R
L Подставим в выражение для полного тока слева - значение i(0), а справа
U
t=0. Получим A . Следовательно, ток в цепи R, L при её коротком
i(0 )
R
t
R
t
1 L - постоянная времени.
замыкании: i U e pt U e L U e , где
p R
R
R
R
-величина, обратная корню характеристического уравнения. За промежуток времени
, ток убывает в e раз. Чем больше , тем медленнее затухает ток.
i, u
U
R
U
Напряжения:
L
i
u
L
t
t
U
di
1U
u iR Re Ue ; u L L(
e ) Ue .
R
L
R
dt
R
t
t
На рис. приведены графики i(t ), u (t ). График uR , если его
L
t
изобразить, расположится зеркально к графику u (t ) в
положительной области.
L
Постоянная времени равна длине подкасательной в любой
t
di
1U
i
e
tg .
точке кривой i(t ), так как
dt
R
83.
Определим энергию W, выделяемую в резисторе сопротивлением R за времяt
2 (0 )
2
2
U 2 2
Li
L
U
W (0 ).
переходного процесса: W i Rdt
Re dt
( 1)
2
M
2 R2
2
0
0R
Энергия, запасённая в магнитном поле индуктивности в момент до коммутации,
выделится в виде тепла на активном сопротивлении после коммутации.
Отключение индуктивной цепи от источника постоянного напряжения
При размыкании рубильников в электрических цепях, содержащих индуктивности,
на отдельных участках цепей могут возникать напряжения, во много раз превышающие установившиеся.
t 0
Цепь из R , R , L питается от напряжения U , причем
1 2
до коммутации R зашунтирован рубильником. Определим
2
U
в момент коммутации.
t 0
a
R2 b R1
U
L
ab
Ток до коммутации: i(0 ) U R1 . В момент коммутации
ток не изменяется i(0) i(0 ) U R1 . Напряжение U
ab
R
2
в момент коммутации: U (0) i(0) R2 U
Если R R , то U (0) U .
.
ab
2
1
ab
R1
Отключение индуктивной цепи от источника можно рассматривать как предельный
случай, когда R , но, при этом, U (0) .
2
ab
Размыкание рубильника происходит не мгновенно и между его контактами возникает электрическая дуга. Это аварийный режим.
84.
Рассмотрим отключение индуктивной катушки от источника постоянного напряжения,Когда на её зажимах включён вольтметр с внутренним сопротивлением R .
V
Определим U (0), если считать, что размыкание происхо-
t 0
R
V R
V
i
V
дит мгновенно и дуга не возникает. Ток до коммутации
U
i
(
0
)
, т. к. R R. В момент коммутации i(0) U
U
R
V
R
и ток будет протекать по контуру R, L, R . Напряжение
V
R
на вольтметре U (0) i(0) R U V . При R R обмотка вольтметра может
V
V
V
R
U
V
L
сгореть. Чтобы не вывести прибор из строя, сначала надо отключить его, а затем
разомкнуть рубильник.
Перенапряжения в индуктивных цепях проявляются тем сильнее, чем больше L.
Включение индуктивной цепи под постоянное напряжение
t 0
U
R
Дано: U , r, L, i(0) 0.
i
L
Найти: ur (t ), uL (t ).
Дифференциальное уравнение: L
di
ir U .
dt
Характеристическое уравнение и его корень
pt
r
L
p ; . Свободная составляющая тока: iсв Ae .
L
r
pt U
U
i
i
i
Ae
.
Принуждённая составляющая тока: i . Полный ток:
св
пр
r
пр r
U
U
Начальные условия: i(0) i(0 ) 0. При t 0, i(0) 0 A , откуда A .
r
r
Lp r 0;
85.
tt
U
i (1 e ); u ir U (1 e ); u Ue .
r
L
r
Следовательно:
i, u , u
r L
Напряжение на резисторе и ток в индуктивности при
подключении её к источнику постоянного напряжения
U
U
t
U
r
U i
L
изменяются не мгновенно, а с постоянной времени
r
t
и тем медленнее, чем больше .
При t 4
ток
достигает 99,3% установившегося значения и
переходный процесс можно считать законченным.
L
r
Включение индуктивной цепи под синусоидальное напряжение
r
Цепь при t 0 включается под синусоидальное напряжение
u(t )
L u(t) U sin( t ). Здесь начальная фаза определяет
u
m
u
i
напряжение в момент включения, т. е., при t 0 , u(0) U sin .
m
u
Определим ток i после коммутации. Составим дифференциальное уравнение цепи:
t 0
di
ir U sin( t ). Характеристическое уравнение и его корень: Lp r 0;
m
u
dt
t
pt
r
L
p ; . Свободная составляющая тока: iсв Ae Ae . Принуждённая
L
r
L
составляющая тока при синусоидальном воздействии равна установившемуся току:
86.
UL
m
i i
I sin( t ), где I
, arctg .
пр уст m
u
m
r
r 2 ( L)2
t
Полный ток: i i i Ae I sin( t ). При t 0,i(0) 0 A I sin( ).
св пр
m
u
m
u
t
Откуда A I sin( ).
m
u
Искомые ток и напряжение: i I sin( t ) I sin( )e ;
m
u
m
u
t
di
r
u L L I [cos( t )
sin( )e ]
L
m
u
u
dt
L
t
r
x I [cos( t ) sin( )e ].
L m
u
u
x
L
i
I sin( )
m
u
t
87.
Переходные процессы в емкостной цепи при постоянном воздействииКороткое замыкание цепи r, C
U
r
0
r
t 0
C
Пусть конденсатор ёмкостью C был заряжен от источника постоянного напряжения до U. В момент t=0 замыкается ключ и конденсатор разряжается через r.
Выберем положительные направления тока и напряжений u , u .
r
c
По второму закону Кирхгофа u u 0.
r
c
du
u
c.
r
u
ir
,
i
i
C
r
Уравнения
связи:
r
c
t 0
dt
u
C
du
c
c u 0.
Дифференциальное уравнение: rC
c
dt
1
Характеристическое уравнение и его корень: rCp 1 0; p
.
rC
t
t
Ae pt Ae rC Ae , где rC -- величина,
Свободная составляющая uc : u
c св
имеющая размерность времени, называемая постоянной времени rC – цепи.
Постоянная времени тем больше, чем больше ёмкость и сопротивление. Т. е. чем
больше C и r , тем медленнее происходит разряд конденсатора
Принуждённая составляющая uc пр здесь равна нулю, так как после окончания переходного процесса конденсатор полностью разрядится. u
0.
c пр
88.
Рассмотрим два частных случая.а) или . Тогда: i I sin t; u I x cos t.
u
u
m
L
m L
В этом случае, свободная составляющая тока отсутствует ( i 0 ) и в цепи
св
устанавливается сразу принуждённый режим без переходного процесса.
i
t
б) u .
2
t
Тогда: i I cos t I e ;
m
m
t
r
u x I sin t rI e U ( sin t e ).
L
L m
m
Lm
x
L
t
i
I
2I
I
m
В этом случае ток в переходном режиме
m
m
t
достигает своего экстремального значения в
конце первого полупериода. В предельном
случае, для контура без потерь, т. е. r 0 ,
, ток достигает двойной амплитуды 2I m .
Во всех других случаях максимальный ток
переходного процесса будет меньше
.
89.
Полное решение дифференциального уравнения: uc uc пр uc св uc св Aet
.
При t=0, с учётом второго закона коммутации: u (0) u (0 ) U A.
c
c
t
t
du
c cU ( 1 )e rC U e .
i
C
Ток в цепи:
dt
rC
r
i, u
c
Определим энергию, выделяющееся в сопротивлении за
время переходного процесса.
U
u (t )
c
t
U r
i(t )
2t
U 2
2
U 2C
rC
W i r dt 2 re dt
W (0 ).
c
0
r
0
r
С энергетической точки зрения, процесс короткого
замыкания цепи rC характеризуется переходом
энергии, запасённой до коммутации в электрическом
поле конденсатора, в тепловую энергию, выделя-
ющуюся на сопротивлении r.
90.
Включение rC- цепи под постоянное напряжениеt 0
U
r
u C
r
i
u
c
В момент t=0 цепь rC подключается к источнику постоянного напряжения U . Пусть конденсатор был предварительно заряжен до U . То есть u (0) U .
c0
c
c0
du
Дифференциальное уравнение: rC c u U .
c
dt
1
Характеристическое уравнение и его корень: rCp 1 0; p
; rC.
rC
pt
Свободная составляющая u
: u
Ae .
c св
c св
Принуждённая составляющая: u
U .
c пр
u
Ae pt U .
Полное напряжение на конденсаторе: u u
c c св c пр
При t=0, u (0 ) u (0) U A U . Откуда A U U .
c c
c0
c0
t
Следовательно, напряжение u при заряде: u U (U U )e .
c
c0
c
t
t
du
U U
c0 e .
Ток в цепи при заряде: i C c C (U U )( 1 )e
c0
dt
rC
r
91.
Построим графики изменения uc (t ) , i(t ) при заряде, считая, что до коммутацииконденсатор не был заряжен, т. е. U 0.
t
U
u U (1 e ); i e .
c
r
Тогда:
t
u ,i
c
c0
u (t )
c
U
U
r
i(t )
t
Для трёх других случаев, когда U 0, графики u (t ) и
c
c0
построить самостоятельно:
а) U
б) U
в) U
c0
c0
c0
i(t ) предлагается
U - подзаряд конденсатора до U ;
U - переходный процесс отсутствует (при соответствующей полярности U
U - разряд конденсатора до U .
c0
);
92.
Включение rC- цепи под синусоидальное напряжениеr
u(t )
t 0
u C
r
i
Цепь включается под действие синусоидального напряжения: u(t ) U sin( t ).
u
c
m
u
Определим закон изменения напряжения u (t ) и тока i(t ),
c
если конденсатор не был предварительно заряжен.
du
Дифференциальное уравнение: rC c u U sin( t ).
c
m
u
dt
Характеристическое уравнение и его корень: rCp 1 0;
Свободная составляющая: u
c св
t
p
1
; rC.
rC
Ae .
Запишем принуждённую составляющую тока, равную установившемуся току:
U
x
m
i i
I sin( t ), где I
, arctg( c ).
m
пр уст m
u
r
1
r 2 ( )2
C
Принуждённая составляющая напряжения:
u
I x sin( t ) I x cos( t ).
c пр m c
u
m c
u
2
93.
tu
Ae I x cos( t ).
c c св c пр
m c
u
При t 0, u (0 ) u (0) 0 A I x cos( ), откуда A I x cos( ).
m c
u
m c
u
c
c
t
Следовательно, uc I m xc[cos( t u ) cos( u )e ];
Полное напряжение: u u
Рассмотрим два частных случая:
а) 2. u I x cos( t 2) I x sin t;
i I cos t.
m c
m c
m
Свободные составляющие uc и i равны нулю, и в цепи наступает сразу
c
u
установившийся режим.
u ,i
c
u
c
t
i
94.
б) 0.u
Тогда:
t
x
u I x ( cos t e ); i I (sin t c e ).
c m c
m
r
u ,u
c c св
u
c св
u
c
I x
m c
t
t
T
Если T (T – период), то uc 2U m 2Im xc.
Это опасный режим.
95.
Разряд конденсатора через цепь RL.U
r
t 0
u
U r L
U
C c
u
L
До коммутации конденсатор был заряжен от источника
постоянного напряжения u (0 ) U . Определим
c
i, u ,u , u после коммутации при условии i (0) 0.
r L C
L
t
di
1
По второму закону Кирхгофа: u u u 0 или ir L u (0) i dt 0.
r L C
dt c
C0
d 2i r di 1
i 0.
Дифференциальное уравнение, описывающее переходный процесс:
2
L dt LC
dt
Характеристическое уравнение и его корни: P2 r p 1 0;
L
LC
r
Обозначим:
- коэффициент затухания контура r L C;
2L
1
0 - собственная частота контура r L C.
LC
p 2 2 ; p 2 2 .
Тогда:
1
0
2
0
pt
p t
1
A e 2 .
Свободная составляющая тока: iсв A1e
2
Принуждённая составляющая тока равна нулю: iпр 0.
r2
1
r
p
.
2
1, 2
LC
2L
4L
96.
ptp t
i A e 1 A e 2 .
св пр 1
2
При t=0, i(0 ) i(0) 0 A A или A A .
1 2
2
1
Полный ток: i i
Для определения
pt p t
Тогда: i A (e 1 e 2 ). ( )
1
A необходимо определить значение первой производной тока в
1
di
момент коммутации, т. е.
dt 0
. Для этого подставим момент времени t=0 в исходное
уравнение, составленное по второму закону Кирхгофа: i(0)r L
di
u (0) 0.
dt 0 c
di
U
. ( )
c
dt 0 L
pt
p t
di
1
A ( p e p e 2 ).
Определим из ( ) производную тока:
2
dt 1 1
di
Подставив в последнее выражение t=0, получим:
A ( p p ). ( )
dt 0 1 1 2
U
Приравняем ( ) и ( ). Получим: A
.
1 L( p p )
1 2
U
Окончательно, ток при разряде конденсатора: i
(e p1t e p2t ).
L( p p )
1 2
2 U
di
U
Напряжения:
ur
(e p1t e p2t ); uL L
( p1e p1t p2e p2t );
p p
dt p p
1 2
1 2
Так как i(0) 0 и u U , то
uc ur uc
U
( p1e p1t p2e p2t ).
p p
1 2
97.
Рассмотрим выражение для тока: iуравнения
p 2 2 ;
1
0
pt
p t
Значит e 1 всегда больше e 2 .
U
(e p1t e p2t ). Корни характеристического
L( p p )
1 2
p 2 2 . - отрицательные, причем p2 p1 .
2
0
Следовательно, ток i, при разряде конденсатора
не изменяет своего направления. Такой однонаправленный разряд называется
апериодическим.
i
Определим момент времени t
m
pt
e 1
U
L( p p )
1 2
p t
e 2
i(t )
, при
котором ток достигает максимального
значения. Для этого производную тока
при t t
приравняем нулю:
m
pt
p t
di
U
1 m p e 2 m)
0
(
p
e
t dt t t
2
L( p p ) 1
m
1
2
1 t
1
pt
p t
m
1
m
2 m , откуда
p
e
p
e
p
p
или
2
1
1
2
p
ln 1
p
p
1
2 .
ln p p t ln p p t ; ( p p )t ln ;
t
1 1m
2 2m
1 2 m
m p p
p
2
1 2
i
m
98.
Рассмотрим, как перераспределяется и рассеивается энергия электрического поляконденсатора при его разряде.
В промежуток времени 0 t t
i
r
L
i
m
C
разряжающегося конденсатора рассеивается в виде тепла на
резисторе и запасается в магнитном поле катушки. Ток нарастает.
C
При t tm , оставшаяся энергия электрического поля разряжающегося конденсатора и энергия , запасённая до этого в магнитном
поле катушки, рассеиваются в виде тепла на резисторе.
r
L
энергия электрического поля
Колебательный режим разряда конденсатора
2
2
2 2
Если , то корни p1, 2 0 j , где 0 , являются
0
U
комплексными.
Ранее получено значение тока: i
(e p1t e p2t ).
L( p p )
1 2
i
Подставим комплексные корни:
t
i
U
L( j j )
(e j e j )
U t
Ue t e j t e j t
e
sin t.
L
L
2j
График тока – затухающая синусоида.
99.
Нелинейные электрические цепиНелинейные элементы электрической цепи
Нелинейным называется элемент электрической цепи, параметры которого зависят
от тока или напряжения. Например, r (i), L(i), C (u). Нелинейной называется цепь,
которая содержит хотя бы один нелинейный элемент.
Нелинейное сопротивление
I
Основная характеристика ВАХ (вольтамперная х-ка), т. е. U ( I ), I (U ).
U
U
a
Участок ab называется падающим участком ВАХ.
b
I
R
ст
Различают статическое Rст и динамическое Rд сопротивления.
I
U
R a 1 ;
ст I
1
R
д
I
U
R
.
д I
100.
Нелинейная индуктивностьЭто, например, катушка с ферромагнитным сердечником. Её характеризует вебер -
L
H, B
I
амперная характеристика.
Рассмотрим катушку с тороидальным сердечником сечением
S и длиной средней линии l . Магнитный поток: BS (Вб).
Потокосцепление: W BSW (Вб). По закону полного тока
Hl WI , отсюда I
l
S
Hl
.
W
Из двух последних выражений
следует: пропорционально B , I
пропорционально H.
Кривая намагничивания ферромагнитного сердечника показывает, что при значительных H сердечник насыщается.
B
H
Введём понятия статической и динамической индуктивностей:
(Вб)
L
ст
L
дин
d
.
L (I ) ; L (I )
дин
ст
dI
I
С учётом явления насыщения сердечника, построим веберамперную характеристику катушки с сердечником.
I (А)
101.
Графические методы расчёта нелинейных цепей при постоянномтоке
1. Метод пересечения характеристик
R
I 0
Пример 1. Дано: E const, R , U (I ) для R . Найти: I , U .
0
U
E
По второму закону Кирхгофа: E IR U .
Н
0
На графике ВАХ строим внешнюю (нагрузочную) характеристику
источника ЭДС в виде прямой U E IR .
0
U
Точка пересечения внешней характеристики и
искомые результаты.
U (I )
E
U
иск
U (I ) даёт
I
I
Iист
иск
I
I
КЗ
E R
0
0
G
0
I
U
G
н
const, G , I (U ) для G . Найти: U , I .
0
н
По первому закону Кирхгофа: I
I I . Или: I I
I .
ист 0
ист 0
Пример 2. Дано: I
ист
102.
I (U )I
I
ист
I
иск
На графике ВАХ строим внешнюю (нагрузочную) характеристику
I .
источника ЭДС в виде прямой I I
ист
U
U
иск
I
G
0
ист
0
Точка пересечения внешней характеристики и I (U )
искомые результаты.
даёт
2. Метод суммирования ВАХ резисторов
I
E
U
E
U
1иск
U
R
1
R
2
U
1
U
Пример. Дано: E const, U (I ), U (I ). Найти: I , U1,U 2.
1
2
Составим исходное уравнение: E U (I ) U (I ).
2
1
2
Построим
суммарную ВАХ и, при заданном E , найдём I , а затем
П
Uо , U . Так как ток через оба резистора одинаков, то суммирова ВАХ 1 2
ние ВАХ производится при одинаковом токе.
U (I )
1
U (I )
2
2 иск
I
I
иск
Если нелинейные резисторы соединены параллельно,
построение суммарной ВАХ производится при одинаковом напряжении.
103.
Расчёт сложной цепи с одним нелинейным элементом.I
Линейная
U
ЭЦ
I
R
1
E
b
R
2
Iн
a
R
3
a
R
н
U
R
Г
b
EГ
E
ab и сопротивления, равного входному сопротивлению
линейного двухполюсника.
I1
E
; U U 2 I1R2 EГ .
R1 R2 хх
R
н
Внутреннее сопротивление эквивалентного генератора:
Г
хх
:
R R
R R R 3 3 .
Г ab 3 R R
3 3
2. Методом пересечения характеристик определяем I н , U н .
I
н
ab хх
Определим U
U н (I )
I
1. Линейный активный двухполюсник можно представить, по
отношению к зажимам a и b выделенной ветви, в виде
последовательного соединения источника ЭДС, с ЭДС, равной
напряжению на зажимах ab (U
) при разомкнутой ветви
a
b
U
EГ
U
н
Расчёт проводится в два этапа. 1. Используется метод эквивалентного генератора. 2. Метод пересечения характеристик.
R
Г
104.
Магнитные цепиМагнитной цепью (МЦ) называется совокупность магнитных тел (участков) из
ферромагнитных материалов и зазоров, в которых создаётся магнитный поток с
помощью обмотки с током или постоянного магнита. МЦ делятся на однородные
и неоднородные.
Вещества
Ферромагнетики
Диамагнетики
Парамагнетики
1
Висмут 1
Платина 1
0,99983
1,00036
Основные величины, характеризующие магнитное поле
Магнитная индукция B - векторная величина, определяемая по силовому воздействию поля на ток. Намагниченность M - магнитный момент единицы объёма
вещества. H - напряжённость магнитного поля. Эти величины связаны соотношением:
B (H M ). (1)
0
В системе СИ размерность B [ Т ] ; 1Т= 1 Вб / М 2.
M H , (2)
где - магнитная восприимчивость.
Размерность H и M [А/М].
105.
Коэффициент для ферромагнитных веществ является функцией H . Подставив(2) в (1) и обозначив
1 , получим: B 0(H H ) 0 H а H , где
- абсолютная магнитная проницаемость; - магнитная постоянная,
а
0
7
характеризует магнитную проницаемость вакуума. В системе СИ 4 10 Гн/М.
0
Магнитный поток через некоторую поверхность S - это поток вектора B через
эту поверхность. B d S . Размерность
[Вб].
S
Основные характеристики ферромагнетиков
Свойства ферромагнетиков характеризует зависимость B от H . Этих зависимостей два типа: а) кривые намагничивания; б) петли гистерезиса.
B
B
r
1 – кривая намагничивания, геометрическое место
гистерезисных петель. 2 – предельный цикл.
B (при H 0) - остаточная индукция;
1
2
H
c
H
r
H (при B 0) - коэрцитивная сила.
c
Участок Br Hc называется кривой размагничивания.
Гистерезис обуславливает потери энергии.
106.
Магнитомягкие и магнитотвёрдые материалыB
H
B
H
Магнитомягкие материалы – круто поднимающаяся кривая намагничивания и малая площадь гистерезисных петель.
Магнитотвёрдые материалы – большая площадь гистерезисных петель.
Магнитомягкие материалы – это электротехничекие стали, пермаллои предназначены для работы при периодически изменяющемся магнитном потоке.
Магнитотвёрдые материалы – углеродистые стали, специальные
сплавы. Они предназначены для изготовления постоянных магнитов.
Закон полного тока
Или первое уравнение Максвелла. Это опытный закон.
H dl I
l
Магнитодвижущая сила (МДС)
МДС- произведение тока на число витков.
F I w [А]
107.
Падение магнитного напряженияПадением магнитного напряжения между точками а и б магнитной цепи называется
линейный интеграл от напряжённости магнитного поля между этими точками:
U
М аб
Тогда:
б
Hdl. Если H const и совпадает с dl по направлению, то Hdl Hdl cos 00.
а
U
б
М аб
H dl H lаб[
а
жения измеряется в амперах.
А
М ][ А]. Следовательно, падение магнитного напряМ
Сравнение электрических и магнитных характеристик
Установим соответствие между электрическими и магнитными величинами.
Электрические величины
ЭДС
E [В ]
Электрическое напряжение U В
Ток
I A
Магнитные величины
F Iw А
МДС
Падение магнитного напряжения U А
М
Магнитный поток Вб
Электрическое сопротивление R
l
Ом
S
Магнитное сопротивление R
Закон Ома
U
I
R
М
U
М
R
М
l
1
]
0S Гн
[
108.
Первый закон Кирхгофаn
k 0
k 1
n
I k 0
k 1
или
Второй закон Кирхгофа
n
m
U
k Ek
k 1
k 1
n
m
Rk I k Ek
k 1
k 1
или
n
m
U
Мk FМk
k 1
k 1
n
m
RМk k FМk
k 1
k 1
Пример. На ферромагнитный сердечник (см. рис.) намотана катушка содержащая w
витков и запитанная током I . Рассчитать магнитную цепь.
l 2
2
l 2
1
l
I
l
3
l 2
1
l 2
2
U
U
U
F Iw;
M1 M 2 M 3 M
R R R R Iw;
M1
M2
M3
M
l
l
l
l
1 2 3 Iw.
а1S1
а2 S 2
а3S3
а0S
U
Так как
B ,
S
l
l
l
l
1 B 2 B 3 B B Iw.
а1 1 а2 2 а3 3 а0
109.
В последнем выражении учтём, что B H .Тогда H l H l H l H l Iw.
11
22
33
n
m
H
l
Fk .
Это выражение можно записать в сокращённом виде: k k
k 1
k 1
То есть, сумма падений магнитных напряжений равна сумме действующих в
магнитной цепи МДС.
Магнитную цепь тогда можно заменить эквивалентной электрической, содержащей
нелинейные элементы, и провести её расчёт, например, методом суммирования ВАХ
резисторов.
R
R
M2
M
1
F
U
M1
U
R
M3 U
M2
M3
R
M
U
M
110.
Пример. Для более сложной разветвлённой цепи.l
1
2
3
l3
2
l
l3
2
1
R
1 M 1
F1
R
M2
R
M2
2
3
R
M
F2
l
2
Магнитная цепь
Эквивалентная электрическая цепь
По первому и второму законам Кирхгофа составляем систему уравнений для
эквивалентной электрической цепи:
Можно переписать систему (1) в виде:
,
1
2
3
(1)
R R F F ,
M1 1 M 2 2 1 2
R R R F .
M 2 2 M 3 3 M 3 2
Остаётся решить эту систему.
,
1 2
3
H l H l F F ,
11 2 2 1 2
H l H l H l F .
22
33
2


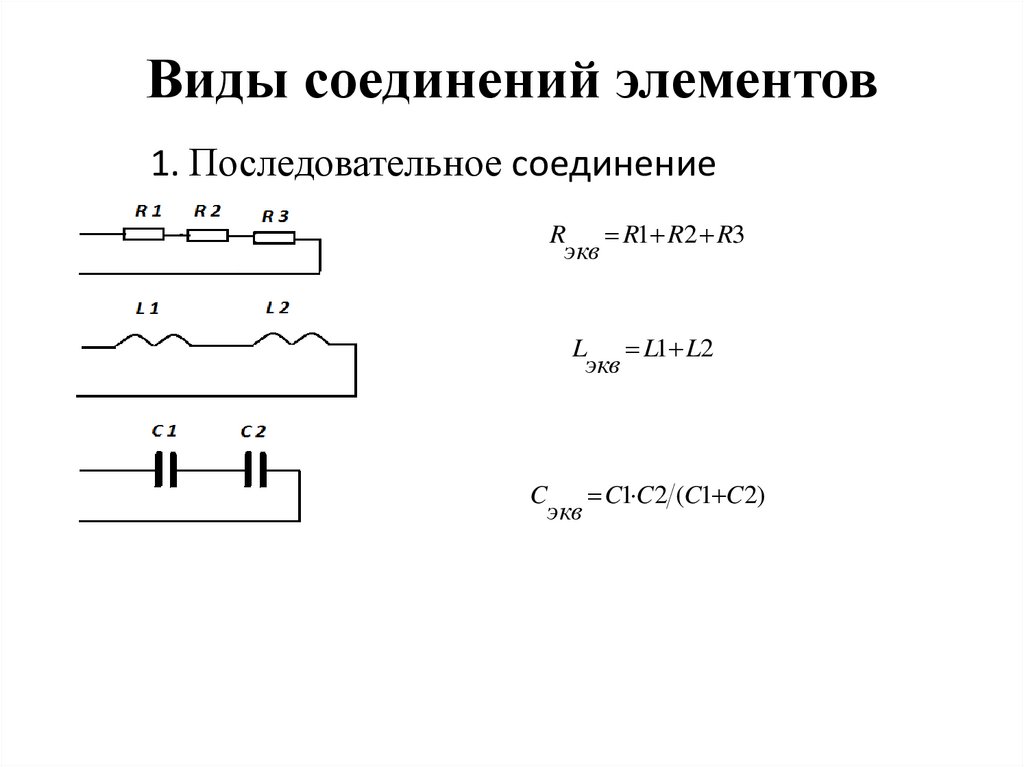

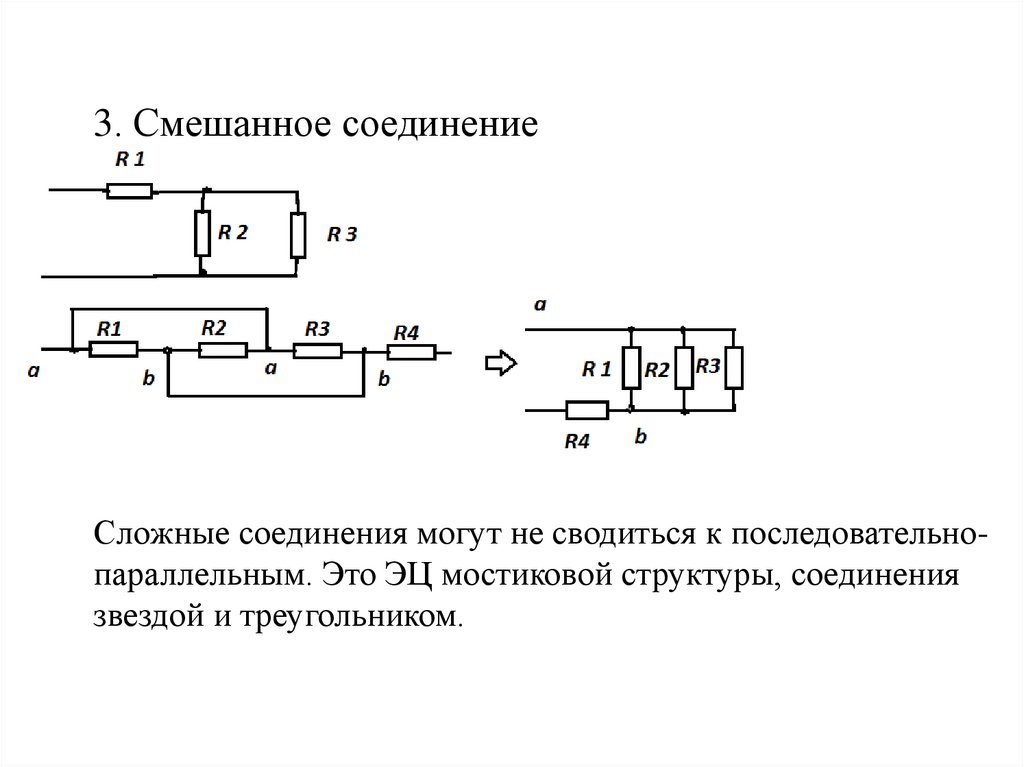












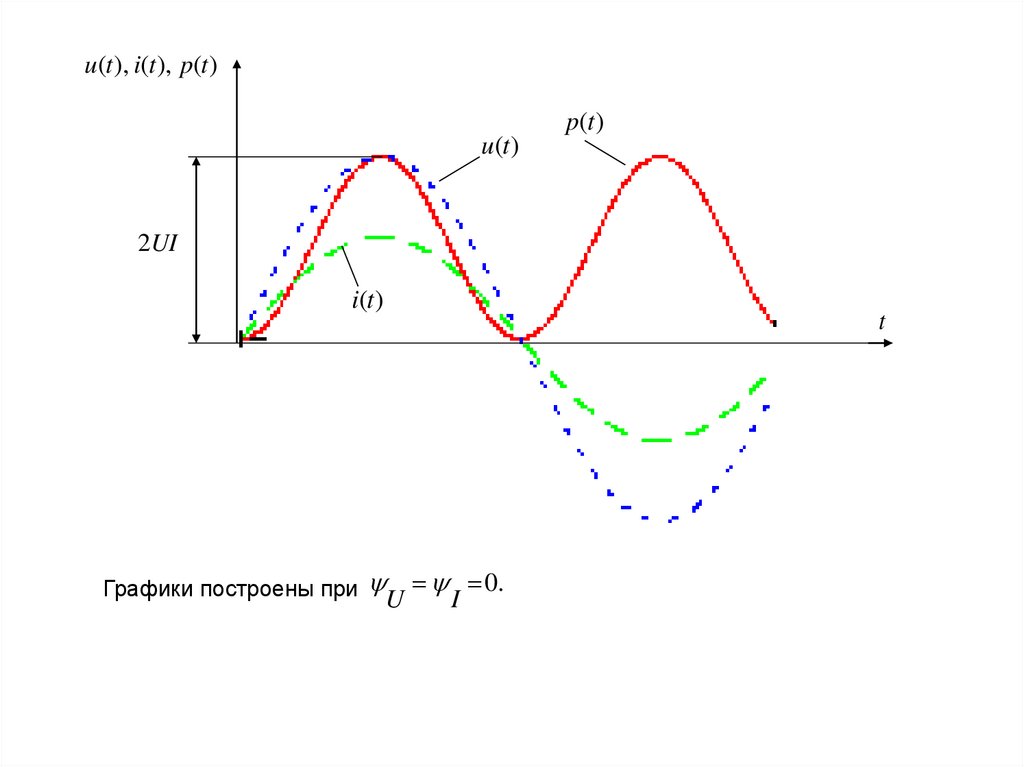

























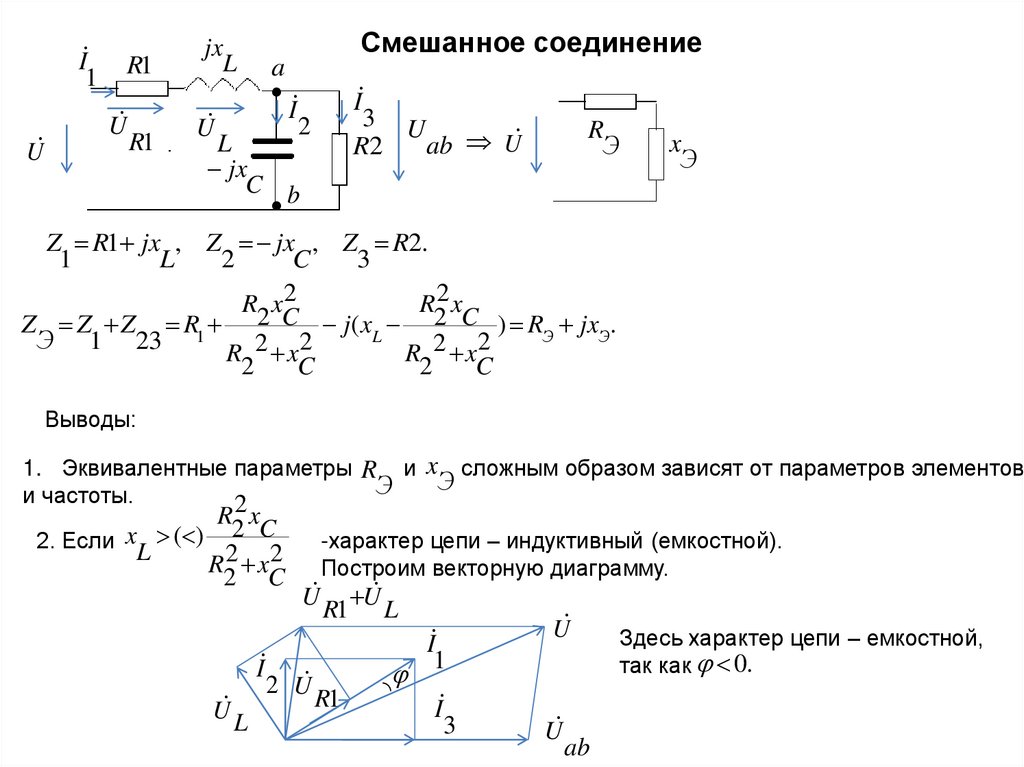
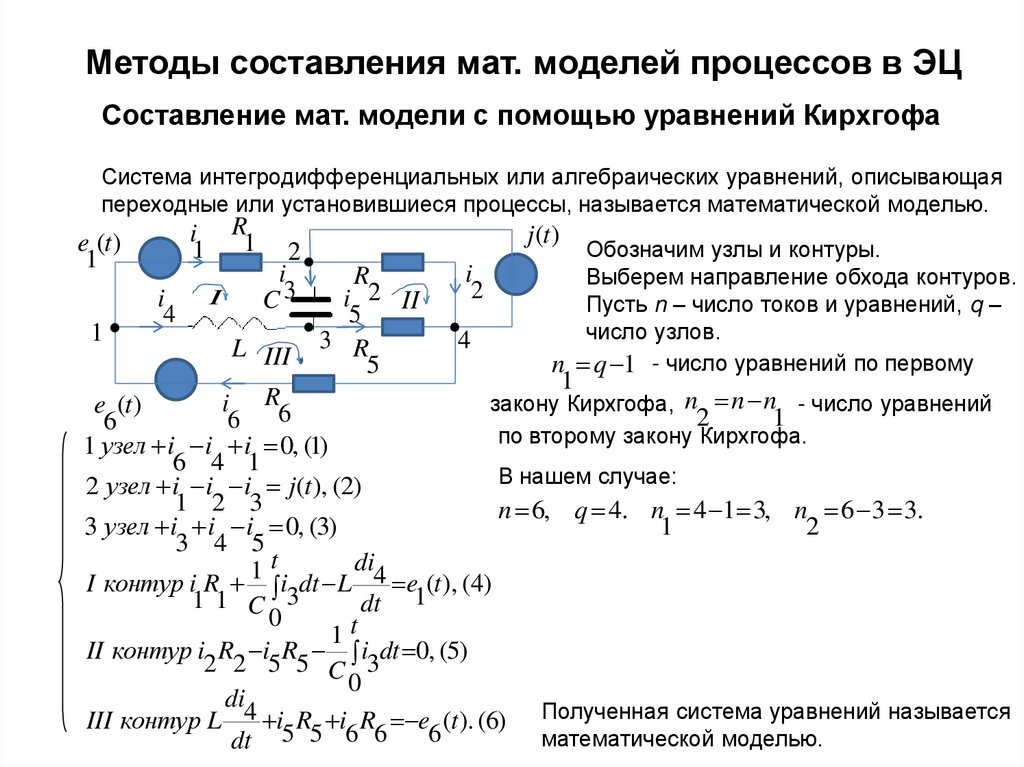


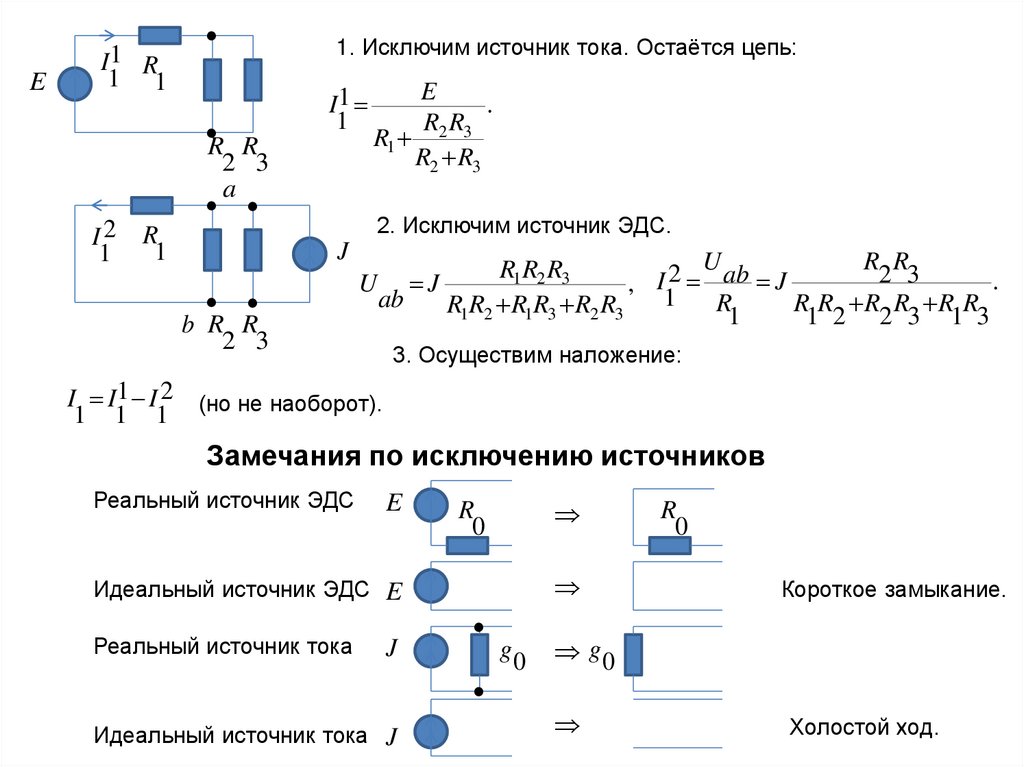




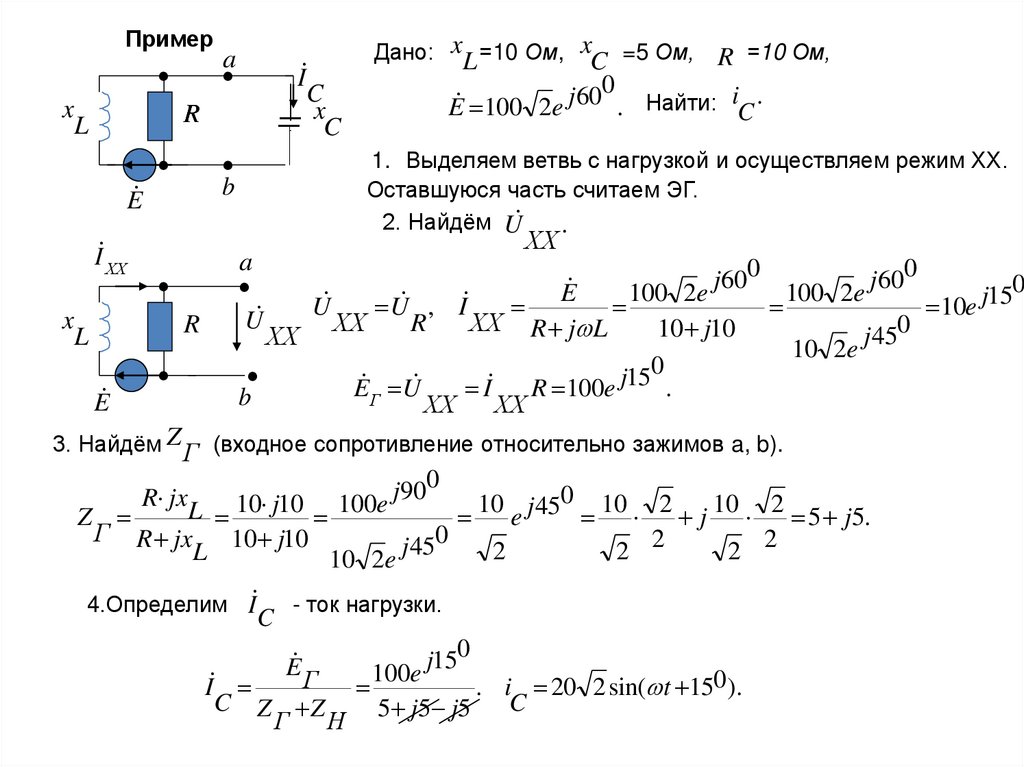







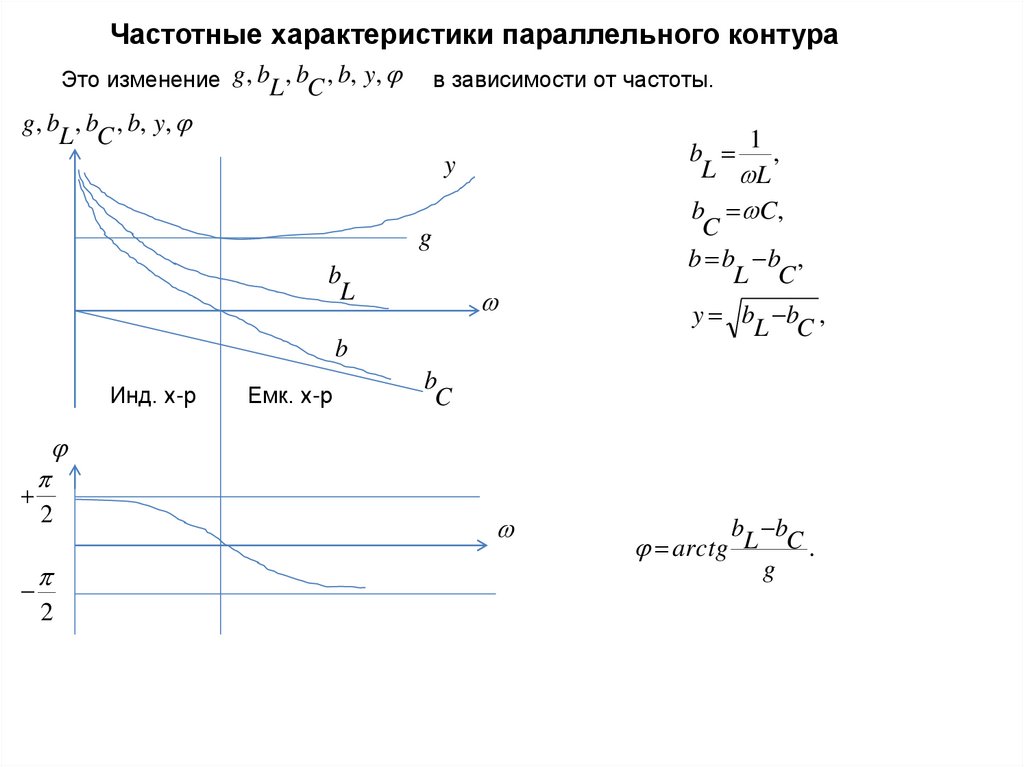






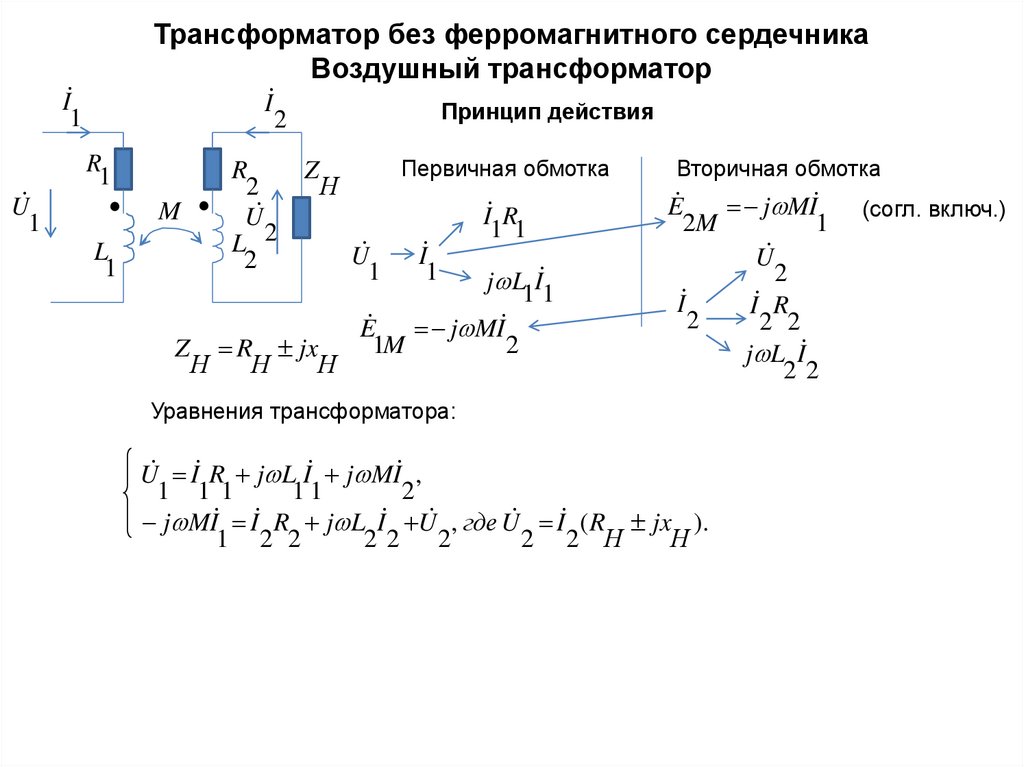



















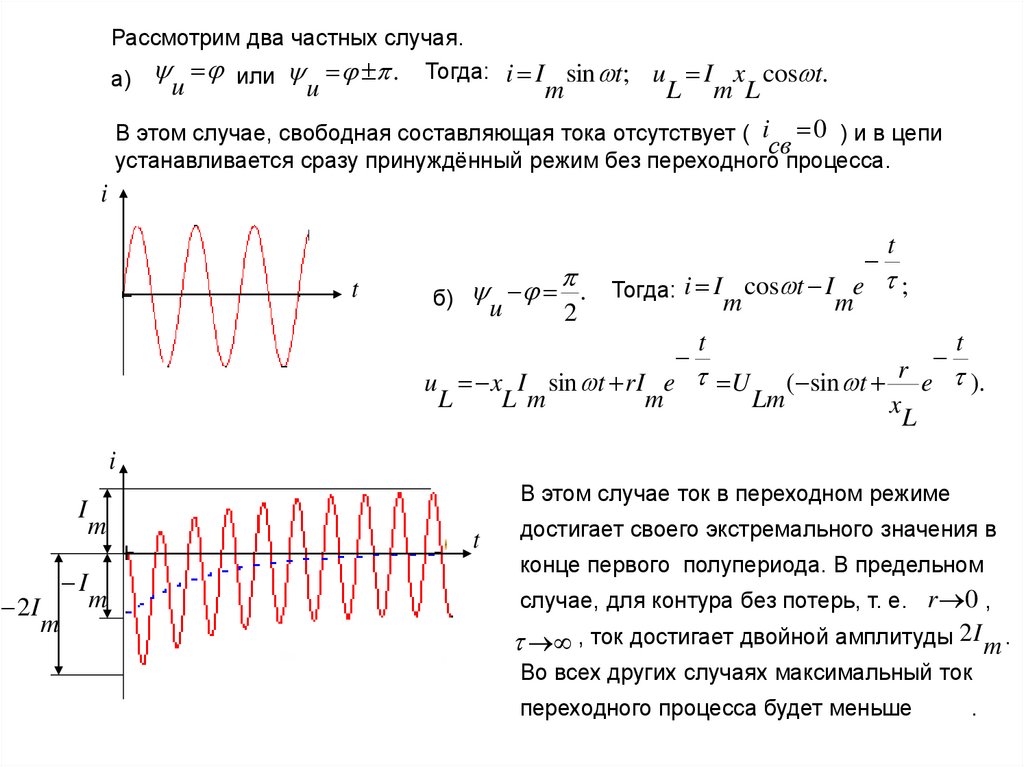








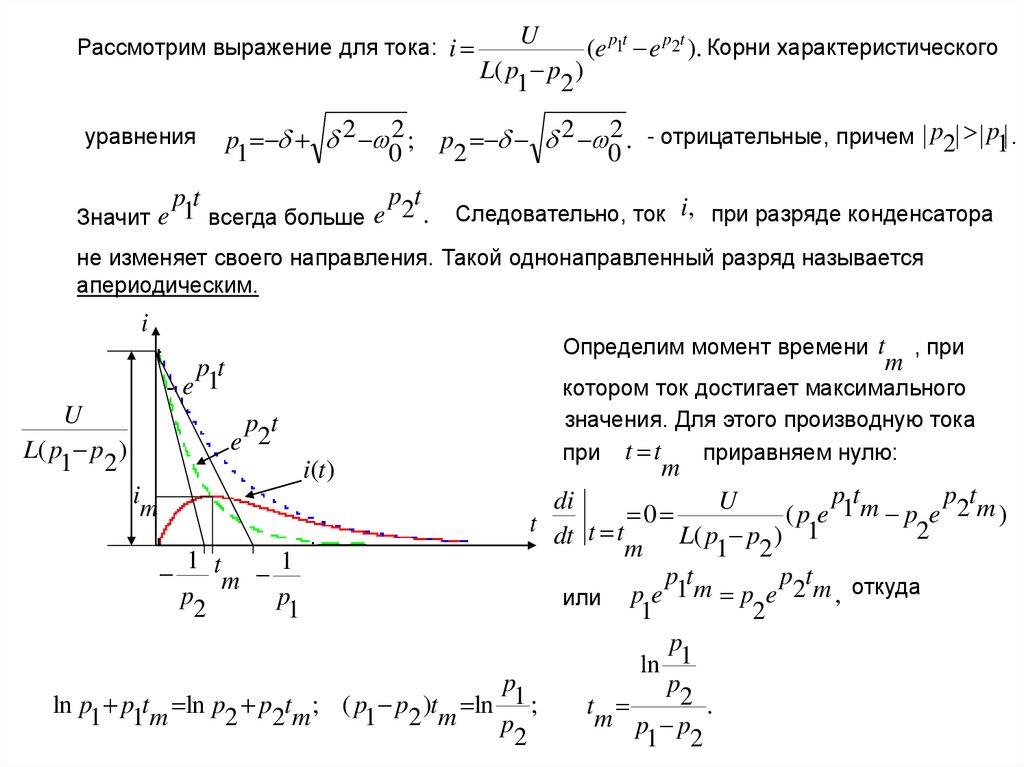

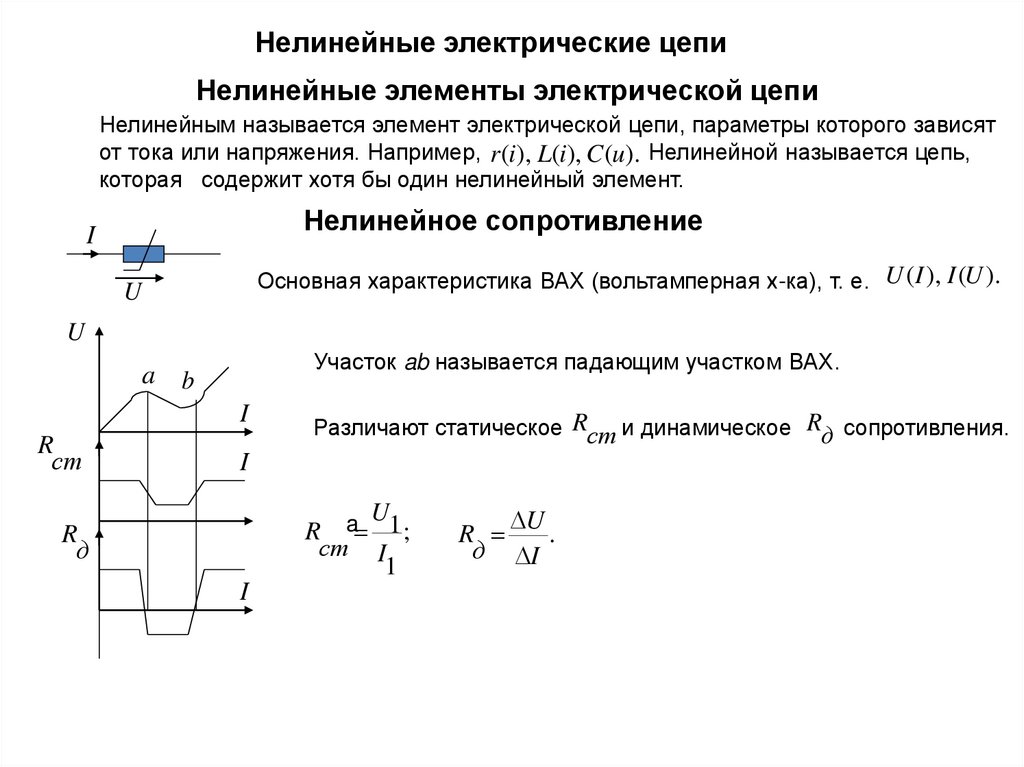




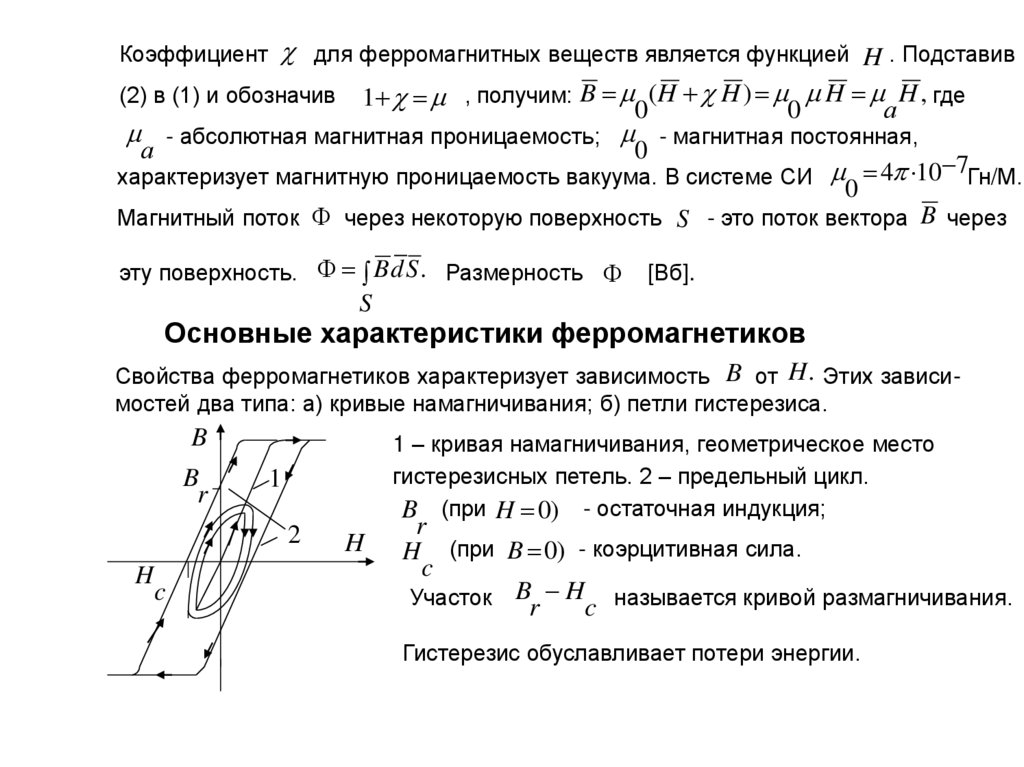





 physics
physics electronics
electronics








