Электротехника. Методы расчёта электрических цепей. (лекция 5)

1.

Конспект лекций по электротехнике
Подготовлен:
Степановым К.С., Беловой Л.В.,
Кралиным А.А., Панковой Н.Г.
Кафедра теоретической и общей
электротехники.
Лекция 5

2. Методы расчёта электрических цепей

3. Метод контурных токов

4. Пусть задана схема, определить токи в ветвях.

R3
R2
R1
R5
R4
I2
I1
E1
I11
E5
E4
I22
I3

5. Метод контурных токов

• При расчете методом контурных
токов полагают, что в каждом
независимом контуре схемы течет
свой контурный ток. Уравнения
составляют относительно
контурных токов, после чего через
них определяют токи ветвей.

6. Метод контурных токов

• Уравнение для первого контура
(R1 R2 )I11 R5 (I11 I 22 ) E1 E5
• Уравнение для второго контура
R5 (I11 I22 ) (R3 R4 )I22 E3 E 4
• Выражения для токов в ветвях
I1=I11; I2=I11-I22; I3=I22.

7. Метод узловых потенциалов

8. Метод узловых потенциалов

• Основан на применении 1-го закона
Кирхгофа
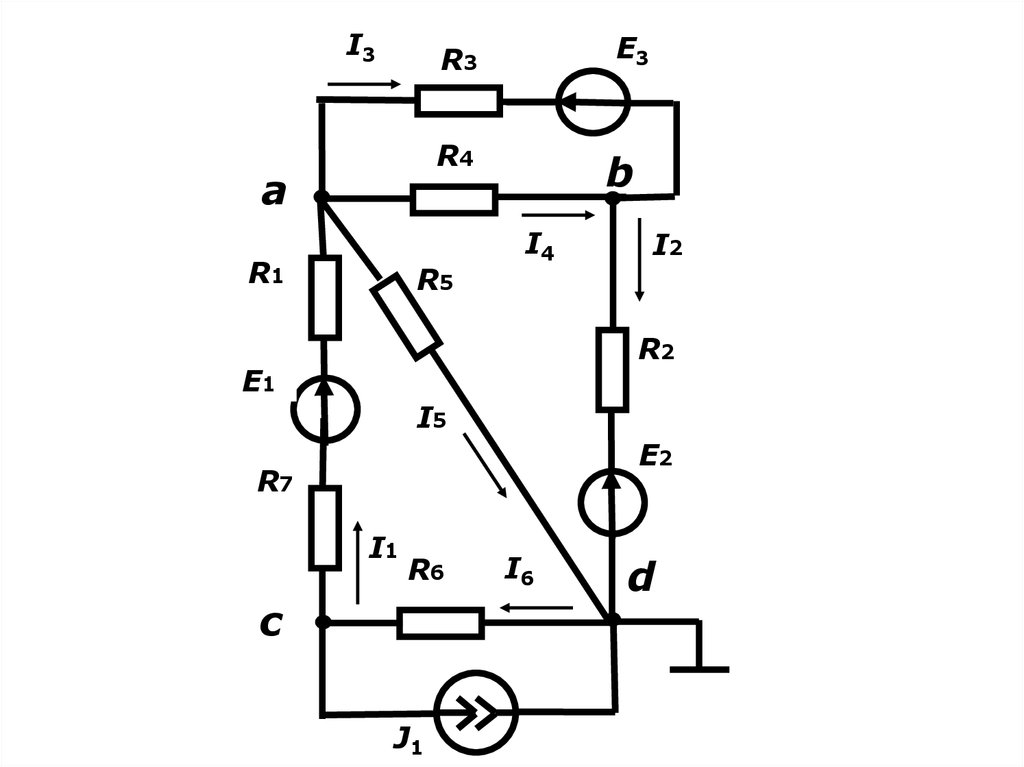
• Пусть требуется составить уравнения
по методу узловых потенциалов для
узлов a,b,c нижеприведённой схемы.
Потенциал узла d приравниваем к 0.

9.

I3
E3
R3
R4
a
R1
R5
b
I4
I2
R2
E1
I5
E2
R7
I1
R6
c
J1
I6
d

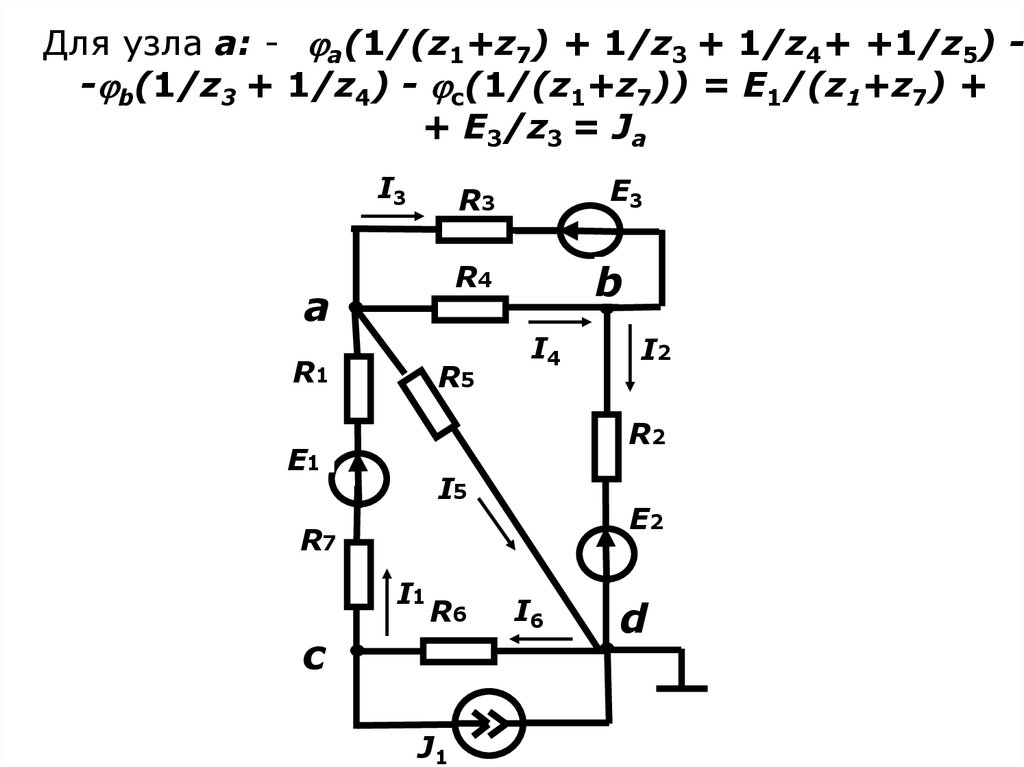
10. Для узла a: - a(1/(z1+z7) + 1/z3 + 1/z4+ +1/z5) - -b(1/z3 + 1/z4) - c(1/(z1+z7)) = E1/(z1+z7) + + E3/z3 = Ja

Для узла a: - a(1/(z1+z7) + 1/z3 + 1/z4+ +1/z5) - b(1/z3 + 1/z4) - c(1/(z1+z7)) = E1/(z1+z7) +
+ E3/z3 = Ja
I3
E3
R3
b
R4
a
R1
R5
I4
I2
R2
E1
I5
E2
R7
I1
R6
c
J1
I6
d

11. Для узла b: -a(1/z3+1/z4)+b(1/z3+1/z4+1/z2)=E2/z2-E3/z3=Jb

Для узла b: a(1/z3+1/z4)+ b(1/z3+1/z4+1/z2)=E2/z2-E3/z3=Jb
I3
E3
R3
R4
a
R1
R5
b
I4
I2
R2
E1
I5
E2
R7
I1
R6
c
J1
I6
d

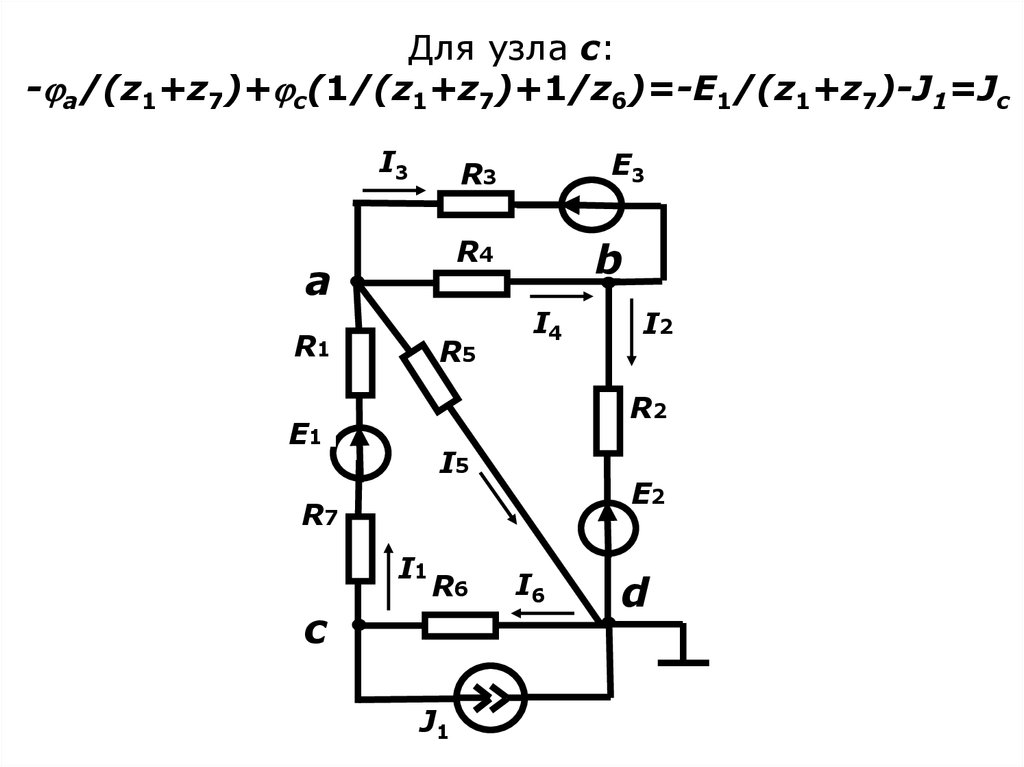
12. Для узла c: -a/(z1+z7)+c(1/(z1+z7)+1/z6)=-E1/(z1+z7)-J1=Jc

Для узла c:
- a/(z1+z7)+ c(1/(z1+z7)+1/z6)=-E1/(z1+z7)-J1=Jc
I3
E3
R3
R4
a
R1
R5
b
I4
I2
R2
E1
I5
E2
R7
I1
R6
c
J1
I6
d

13. В общем виде уравнение для k-го узла:

k kl l kl kl k J k
l
l
l
l
Ykl - сумма узловых проводимостей k-го узла,
представляя собой сумму проводимостей ветвей,
подключенных к k-му узлу. Это собственная проводимость k-го узла.
Jk - алгебраическая сумма источников токов
ветвей, подключённых к к-му узлу.
Ek*Ykl - алгебраическая сумма произведений E
ветвей, сходящихся в k-м узле на проводимости
этих ветвей.

14. Правило: Если ЭДС E, или ток источника J направлены к узлу, то в правой части уравнения перед этими слагаемыми ставится знак .

Правило:
Если ЭДС E, или ток источника J
направлены к узлу, то в правой части
уравнения перед этими слагаемыми
ставится знак .
Система уравнений для
потенциалов узлов будет иметь
вид:
• a Yaa+ b Yab- c Yac=Ja
• a Yba+ b Ybb=Jb
• a Yca+ c Ycc=Jc

15. Метод узловых потенциалов

• Решая систему относительно
потенциалов и тогда токи в ветвях
определяться следующим образом:
• I1=( c- a+E1) 1 ;
I2 b 2 2 ;
I4=( a- b 4 ;
I5= 5 a ;
• I3=( a- b-E3) 3 ;
I6= 6 c .

16. Переменный ток.

17.

18.

19.

20. ПЕРЕМЕННЫЙ ТОК

• Переменным током называется ток,
величина и направление которого
изменяются во времени.
• Мгновенное значение переменного тока
определяется выражением:
2
i(t ) I m sin( t i ) I m sin( t i )
T

21. ПЕРЕМЕННЫЙ ТОК

• Действующим значением переменного тока
называется среднеквадратичное значение тока
за период
Действующее значение переменного тока
Измеряют приборы электромагнитной системы
I
1T 2
i dt
T 0
Im
1T 2
2
I m sin tdt
T 0
2

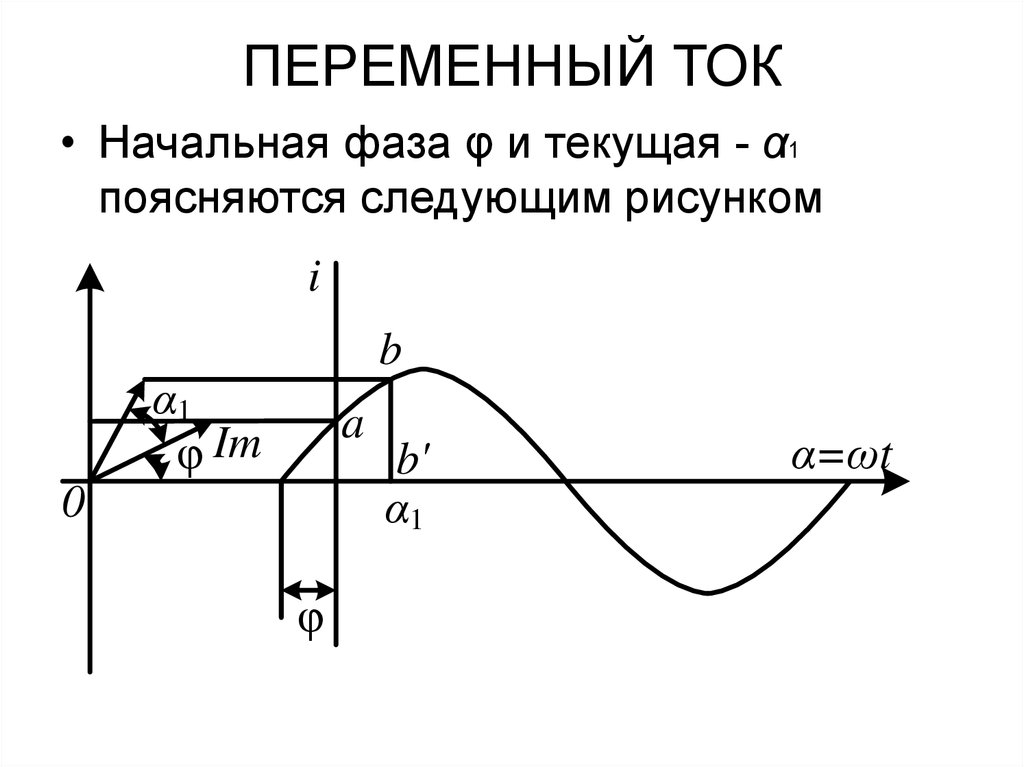
22. ПЕРЕМЕННЫЙ ТОК

• Начальная фаза φ и текущая - α1
поясняются следующим рисунком
i
b
α1
φ Im
a
0
φ
b'
α1
α=ωt

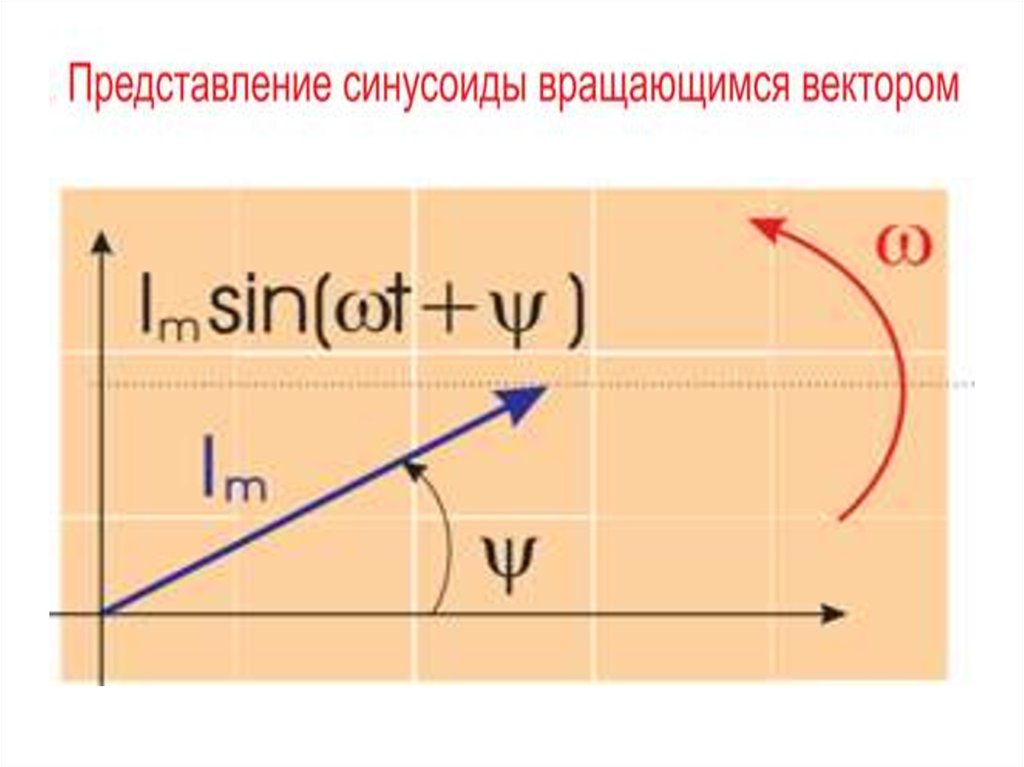
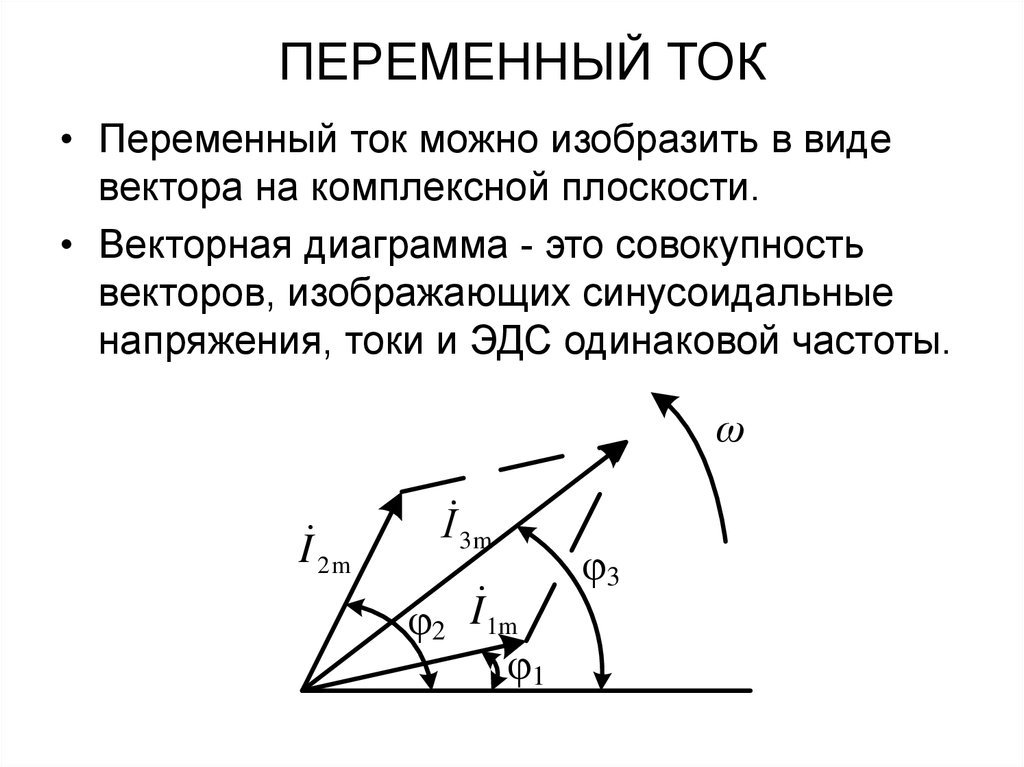
23. ПЕРЕМЕННЫЙ ТОК

• Переменный ток можно изобразить в виде
вектора на комплексной плоскости.
• Векторная диаграмма - это совокупность
векторов, изображающих синусоидальные
напряжения, токи и ЭДС одинаковой частоты.
ω
I 2 m
Ι 3m
I
φ2 1m
φ1
φ3

24. Активное сопротивление на переменном токе

• Пусть по активному сопротивлению
протекает ток i(t)=Im sin t.
• По закону Ома падение напряжения на R
равно u(t) = R·i(t) = R·Imsin t = Um Rsin t
Мгновенная мощность
Im U m
(1 - Cos2 t)
pR(t) = i(t) u(t )= Imsin t Umsin t =
2

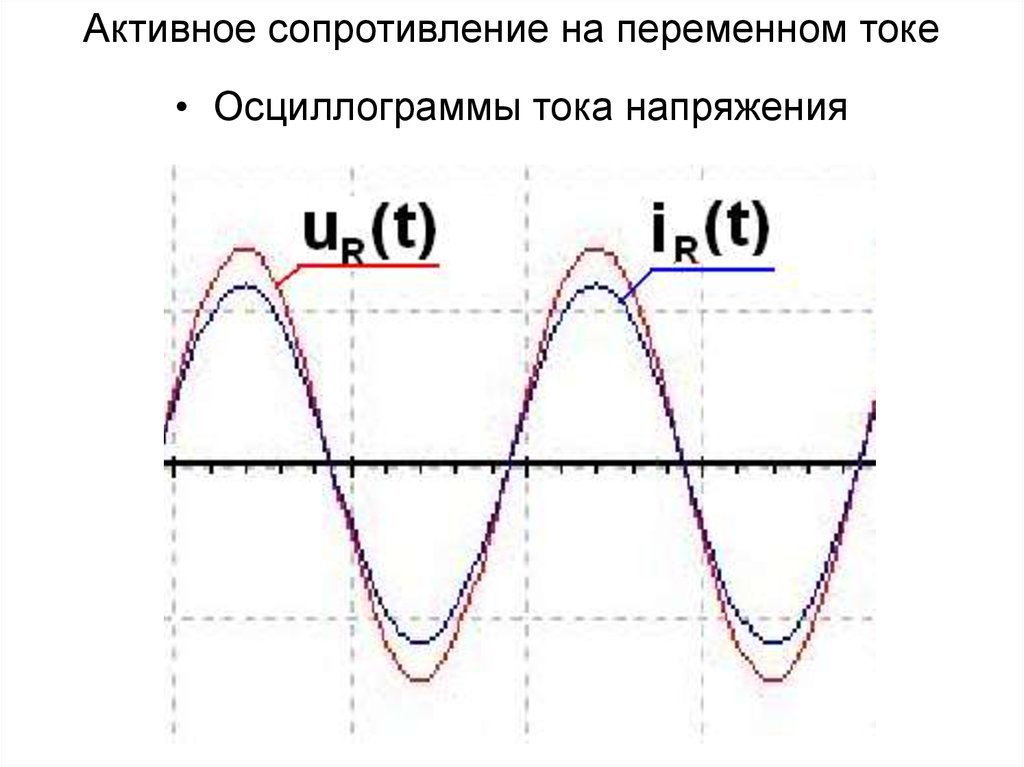
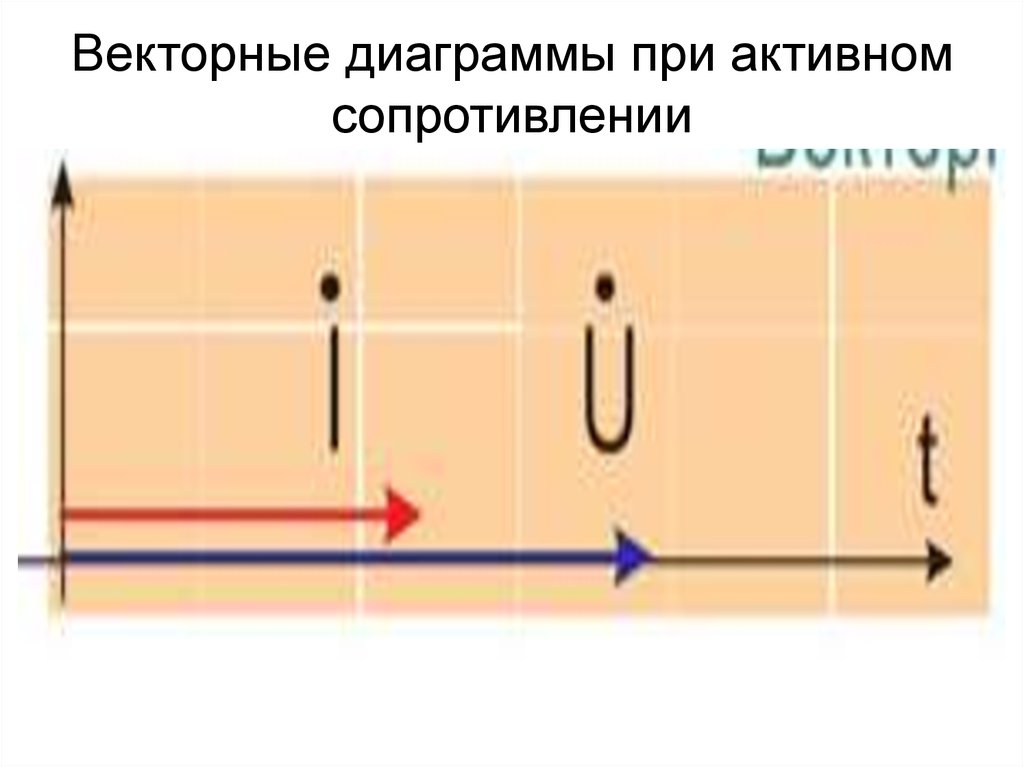
25. Активное сопротивление на переменном токе

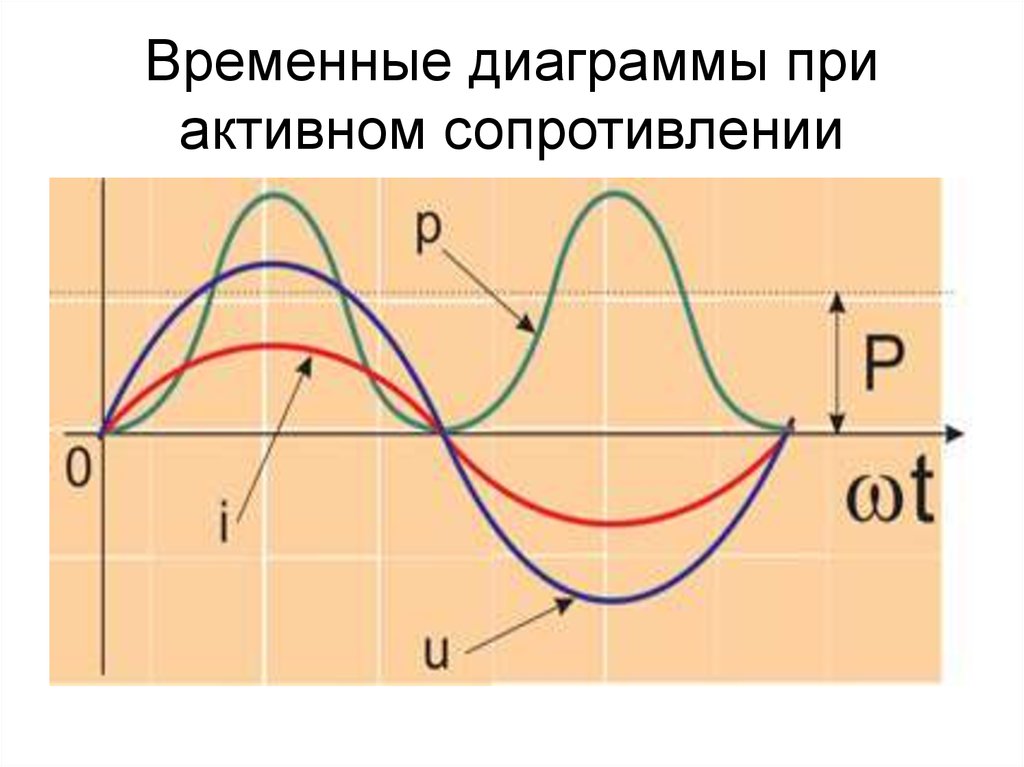
• Осциллограммы тока напряжения

26. Временные диаграммы при активном сопротивлении

27. Векторные диаграммы при активном сопротивлении

28. Индуктивное сопротивление на переменном токе

di
u L e L L
dt
Возьмём первую производную от
синусоидальной функции тока и получим
uL(t) = L di(t)/dt = L Im cos t = XLIm cos t =
= Um sin( t+ /2)
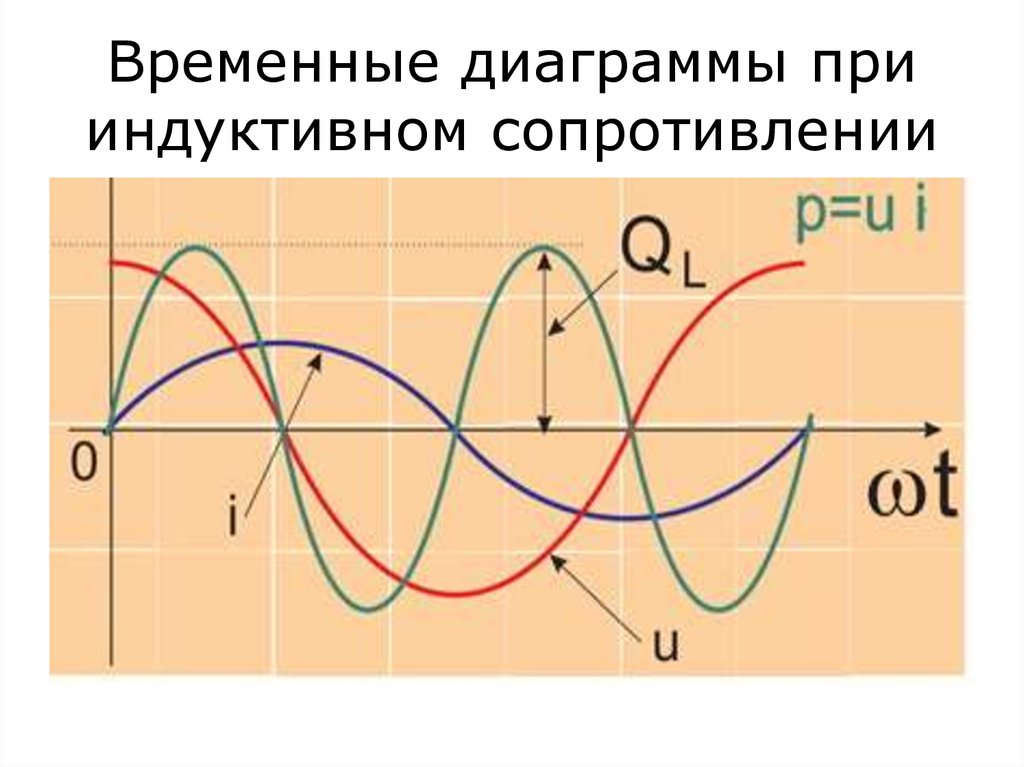
Мгновенная мощность на индуктивностии
pL(t) = i(t) u(t) = Imsin t Umsin( t+ /2) =
= (ImUm/2)sin2 t

29. Временные диаграммы при индуктивном сопротивлении

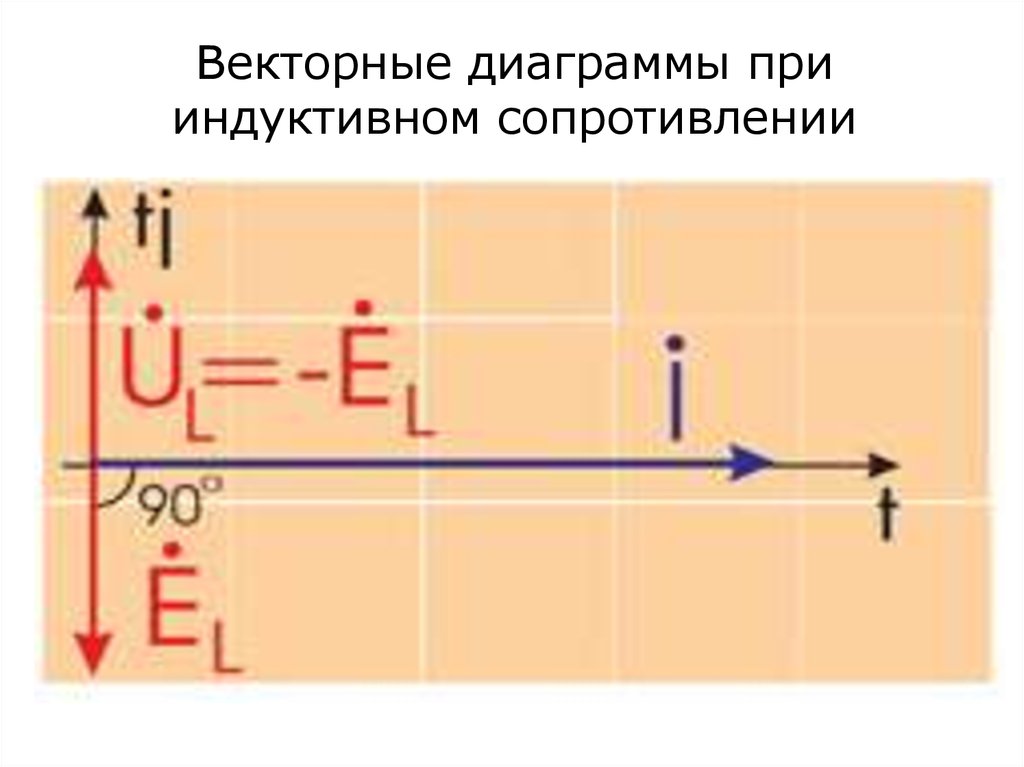
30. Векторные диаграммы при индуктивном сопротивлении

31. Емкостное сопротивление на переменном токе

1
u idt
C
Возьмём интеграл от синусоидальной
функции тока и получим
u(t) = 1/c i(t)dt = 1/ c Im(-cos t) =
= XcImsin( t- /2) = Um sin( t- /2)
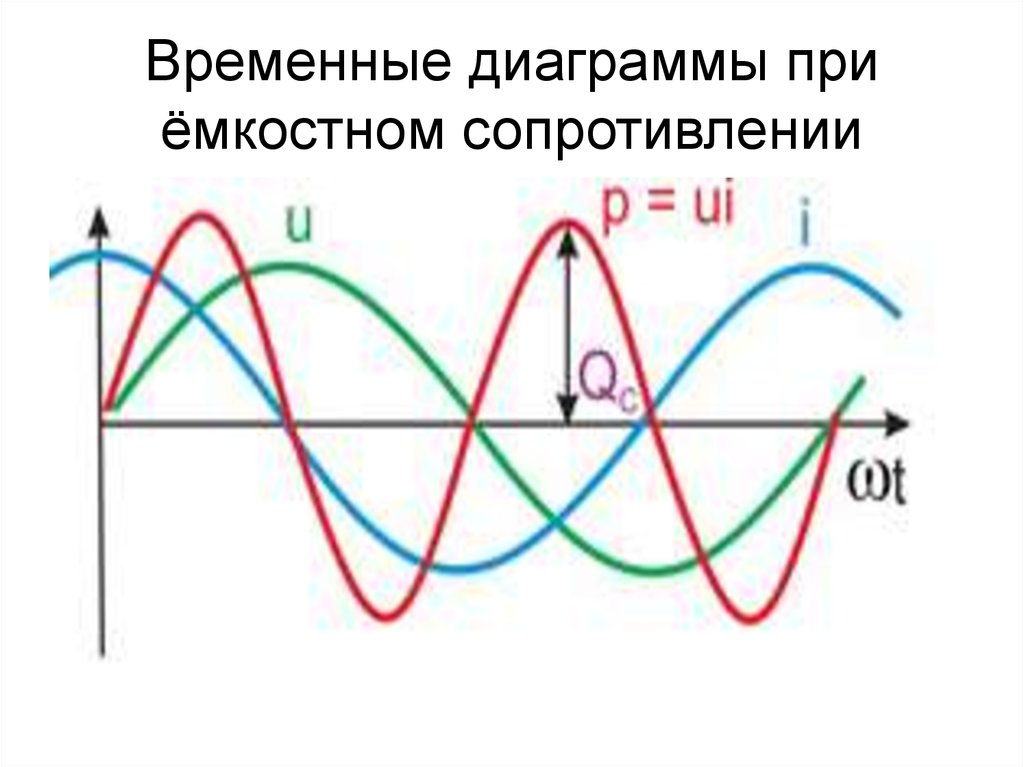
Мгновенная мощность на ёмкости
pc(t) = ImUm/2(-sin2 t)

32. Временные диаграммы при ёмкостном сопротивлении

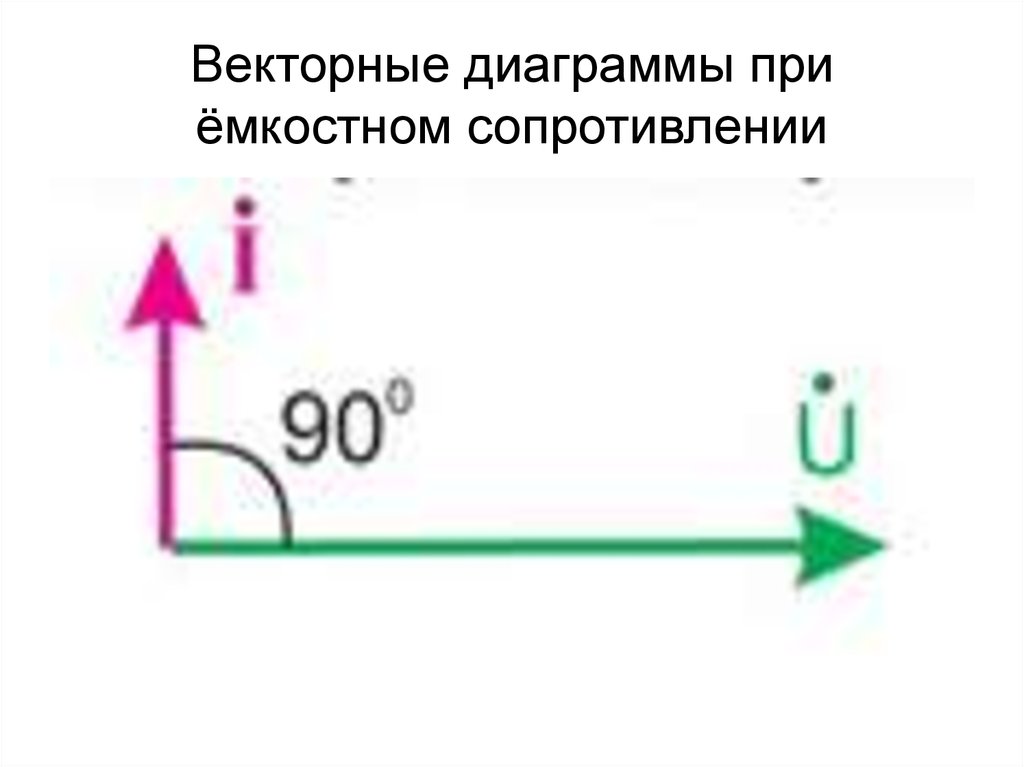
33. Векторные диаграммы при ёмкостном сопротивлении

34. Символический метод анализа линейных цепей на синусоидальном токе

• Есть две основные формы записи
комплексных чисел
j
• Показательная
C ce
• Алгебраическая
a jb
C

35. Символический метод анализа

• С помощью формулы Эйлера можно
перейти от показательной формы
записи комплексного числа к
алгебраической:
ce c cos jc sin a jb
j
a c cos
b c sin

36. Символический метод анализа

• От алгебраической формы записи
переходят к показательной форме
с помощью формул
2
с a b
2
.
b
φ = arctg
a

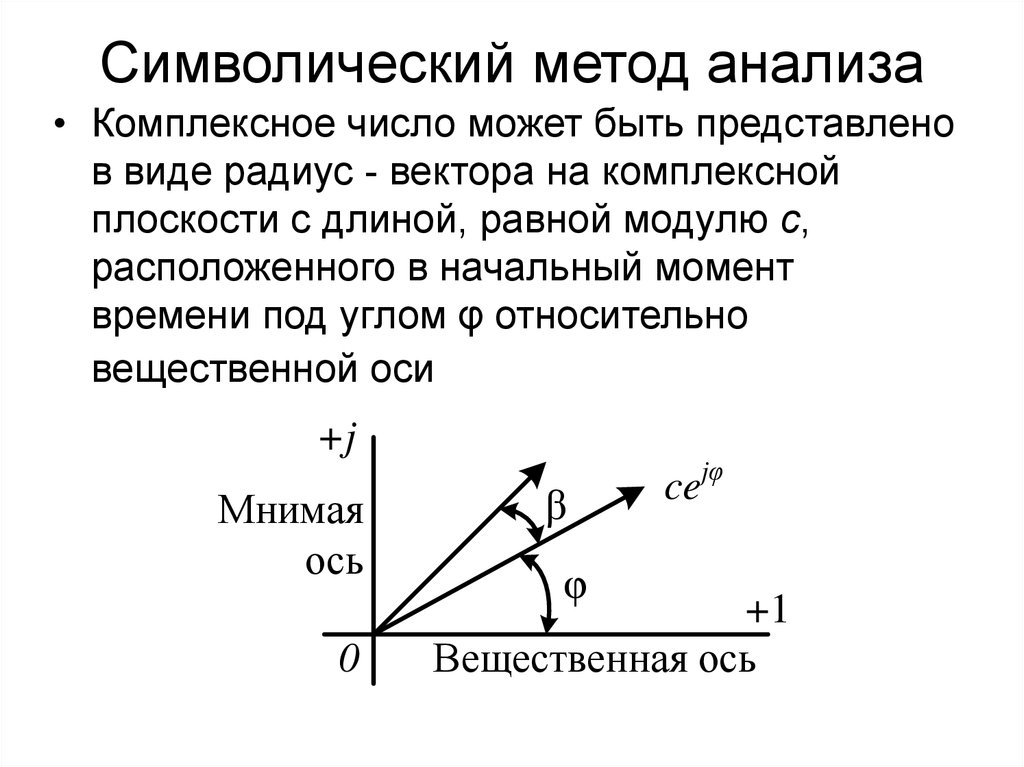
37. Символический метод анализа

• Комплексное число может быть представлено
в виде радиус - вектора на комплексной
плоскости с длиной, равной модулю c,
расположенного в начальный момент
времени под углом φ относительно
вещественной оси
+j
Мнимая
ось
0
β
φ
cejφ
+1
Вещественная ось

38. Символический метод анализа

• Два комплексных числа, имеющие
равные модули и равные, но
противоположные по знаку аргументы,
называют комплексно сопряжёнными
числами. Если исходное комплексное
j
число , C a1 jb 2 ce
то
комплексно сопряжённым числом будет
*
С a1 jb2 ce
j

39. Свойства комплексно сопряжённых чисел

*
Re( C )=(C С)/2
*
Im(C )=( C С )/2j.
*
2
C С с

40. Операции в комплексными числами

• При сложении и вычитании комплексных
чисел используют алгебраическую форму
записи.
• При умножении и делении комплексных
чисел используют показательную форму
записи.
• Пример: сложение
Их сумма
a jb
C
1
1
1
a jb
C
2
2
2
a a jb jb
C
Ý
1
2
1
2

41. Операции в комплексными числами

• Умножение
C c e j 1
1
1
j 2
C2 c2e
j 1 2
C1 C 2 c1 c 2 e

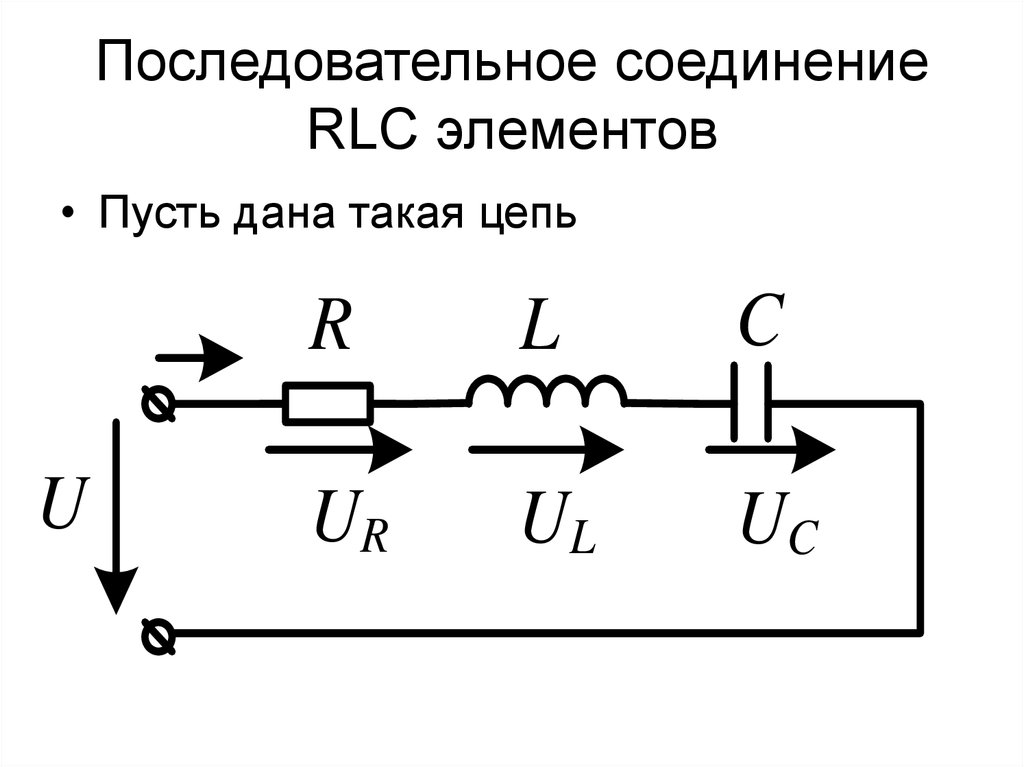
42. Последовательное соединение RLC элементов

• Пусть дана такая цепь
U
R
L
C
UR
UL
UC

43. Последовательное соединение RLC элементов

• Второй закон Кирхгофа в комплексной
форме для этой цепи
j 90
j 90
.
U m RI m X L I m e
X c I me
Полное сопротивление
U
Z
R j X L X c
I

44. Последовательное соединение RLC элементов

• Условие резонанса напряжений
xL = xC;
L = 1/ С
Резонансная частота
0
1
L C
1
f0
2 L C

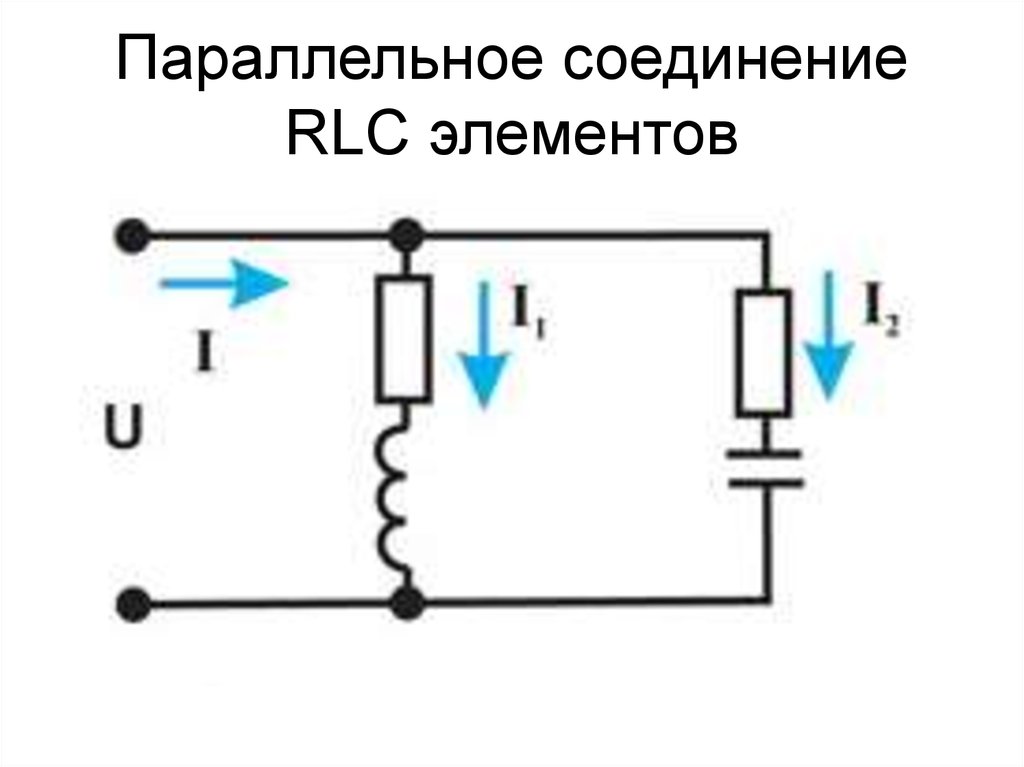
45. Параллельное соединение RLC элементов

46. Параллельное соединение RLC элементов

• При параллельном соединении
складывают проводимости
1
j
Y j ye y cos jy sin g jb,
ze
g
R
2
R X
2
,
X
b 2 2,
R X

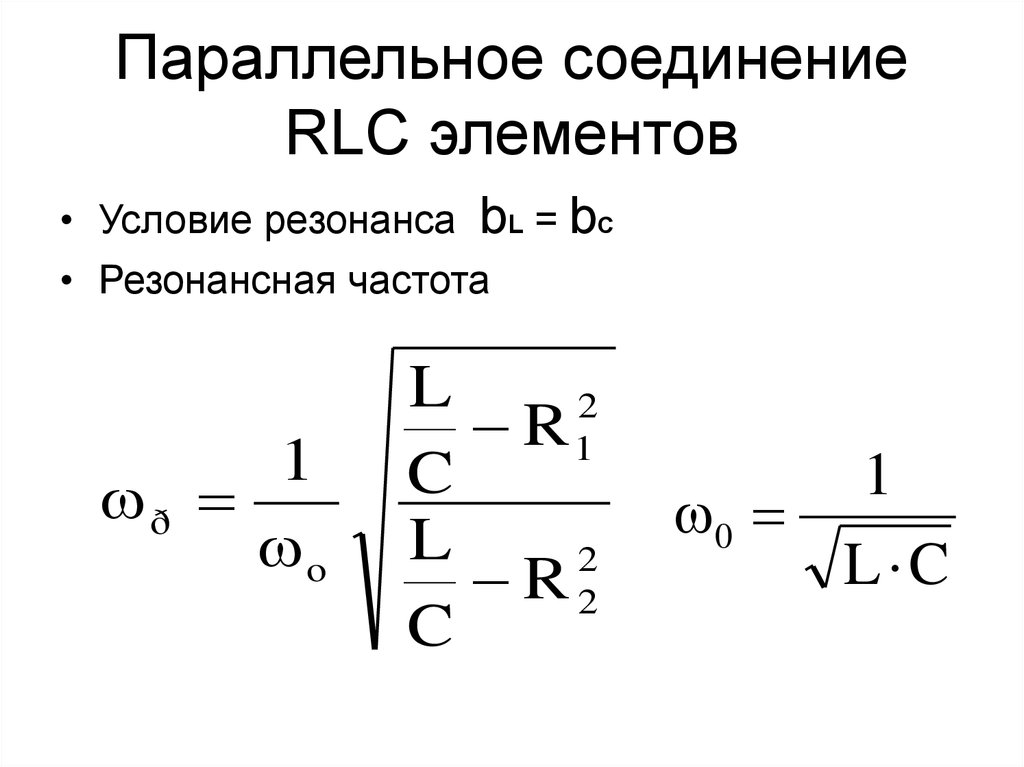
47. Параллельное соединение RLC элементов

• Условие резонанса
bL = bC
• Резонансная частота
1
ð
o
L
2
R1
C
L
2
R2
C
1
0
L C

48.

•ТРЁХФАЗНЫЕ ЦЕПИ

49.

50. Трёхфазные осциллограммы

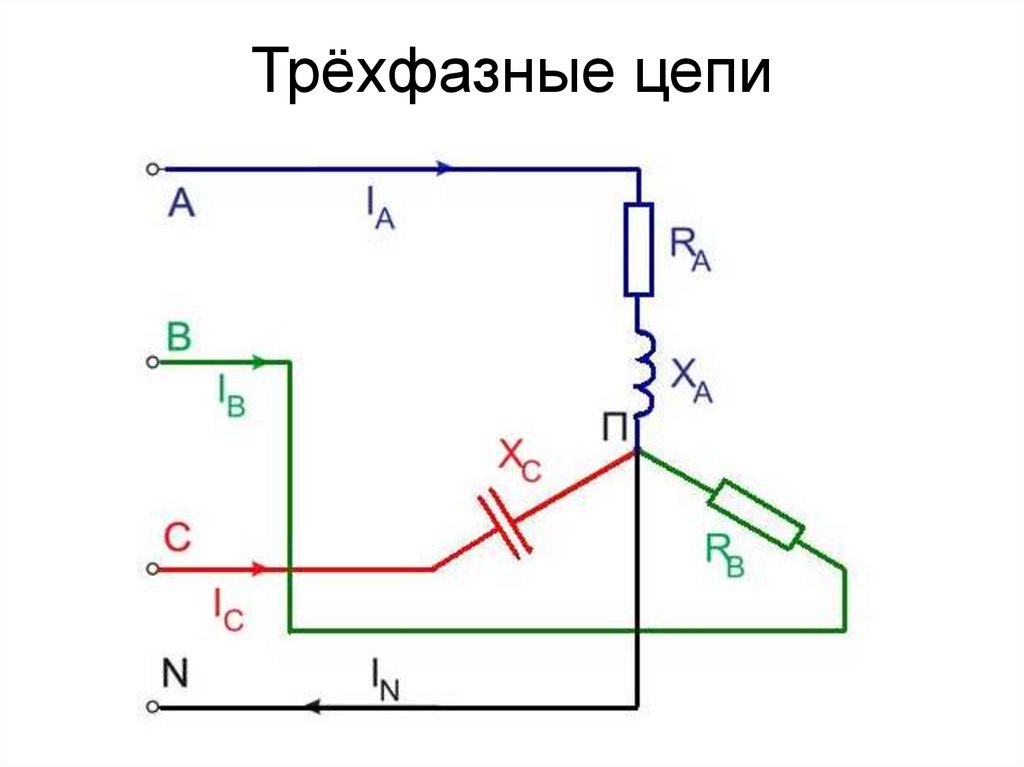
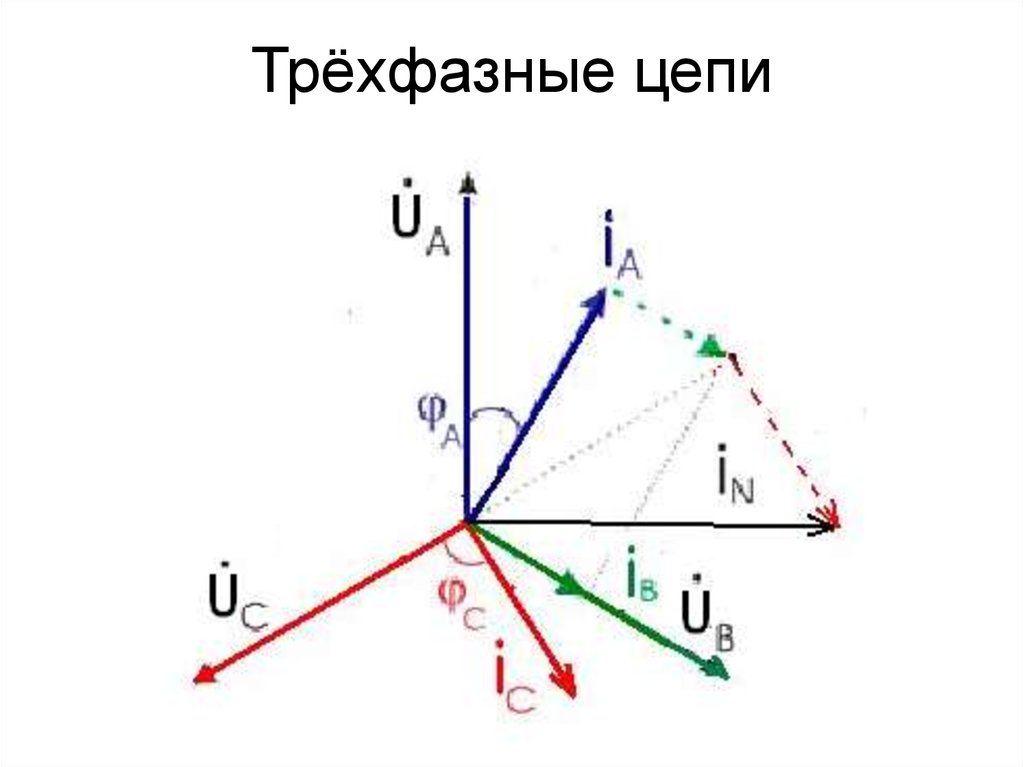
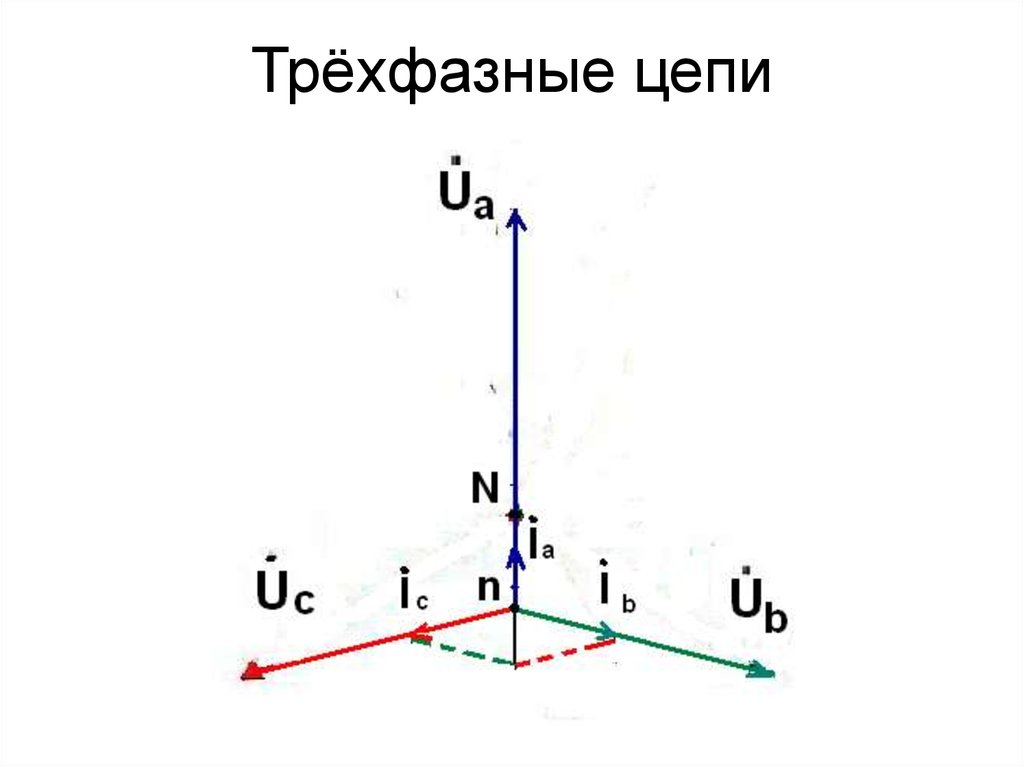
51. Трёхфазные цепи

52. Трёхфазные цепи

53. Трёхфазные цепи

• Если в нейтрального провода не будет,
или в нем будет будет сопротивление
Z, то появится
• Напряжение смещения нейтрали:
где Y=1/Z, Ua,Ub,Uc-фазные
напряжения
U
nN
Y U
Y U
Y
U
a
b
c
A
B
C
Y a Y b Y c Y nN

54. Трёхфазные цепи

55. Литература

• Алтунин Б.Ю., Кралин А.А. Электротехника и
электроника. Ч.1. Н.Н.: Издательство НГТУ 2007г.
• Веселовский О.Н., Шнейберг Я.А. Очерки по
истории электротехники. М.: Издательство МЭИ
1993г.
• Касаткин А.С., Немцов М.В. Электротехника. М.:
Высшая школа 2002г.

56. Благодарю за внимание