Классификация электрических цепей

1. Классификация электрических цепей

1. В зависимости от числа выводов
на двухполюсники, четырехполюсники, многополюсники
(полюсов): делятся
2. В зависимости от характера элементов, входящих в электрическую цепь, различают:
1) Линейные цепи. Эти цепи состоят только из линейных элементов, т.е. элементов, параметры которых не зависят от токов и
напряжений на них. Все линейные элементы имеют линейные вольт-амперные характеристики
Процессы в таких цепях описываются линейными дифференциальными уравнениями с постоянными коэффициентами.
2) Нелинейные цепи. Эти цепи содержат нелинейные элементы, т.е. элементы, параметры которых зависят от токов и напряжений на
них. Все нелинейные элементы имеют нелинейные вольт-амперные характеристики (рис. 4.19). Процессы в таких цепях описываются нелинейными
дифференциальными уравнениями с постоянными коэффициентами.
3) Параметрические цепи. Это цепи, в состав которых входят параметрические элементы, т.е. элементы, параметры которых
изменяются во времени (например, микрофон). Процессы в таких цепях описываются нелинейными дифференциальными уравнениями с
переменными коэффициентами.
3. В зависимости от соотношения длины электромагнитной волны λ и
геометрических размеров электрической цепи L различают цепи с сосредоточенными и
распределенными параметрами.
λ – это путь, который проходит волна за период T. λ = cT = c/ , где c – скорость света, – частота. Длина волны зависит
от частоты сигнала.
а) Цепи называются цепями с сосредоточенными параметрами, если λ >> L. В них все процессы
преобразования энергии сосредоточены в элементах. В таких цепях токи и напряжения в различных сечениях цепи зависят только от времени и не
зависят от координаты сечения х. Процессы в таких цепях описываются дифференциальными уравнениями в полных производных.
б) Цепи называются цепями с распределенными параметрами, если λ ≤ L,. В них элементы R, L, C
необходимо рассматривать распределенными в пространстве. Токи и напряжения в таких цепях зависят от времени и координаты. Процессы в таких
цепях описываются дифференциальными уравнениями в частных производных.
1
4. В зависимости от наличия в цепях активных элементов различают пассивные и активные
цепи. Активные цепи содержат источники (активные элементы), а пассивные их не содержат. Активные цепи делят на автономные и неавтономные.
Автономные цепи содержат независимые источники, а неавтономные содержат только зависимые источники.

2. Основные свойства ЭЦ

4.6. Основные свойства линейных цепей
Свойство 1. В линейных цепях выполняется принцип суперпозиций, т.е.
отклик линейной цепи на сумму воздействий равен сумме откликов на
действие каждого воздействия в отдельности. Рассмотрим линейную цепь (рис.
4.21). Рассмотрим линейную цепь вида: у = kх.
Если x(t) = x1, то y = y1= kx1; если x(t) = x2, то y = y2= kx2;
если x(t) = x1+x2, то y = kx1+kx1 = y1+y2.
Свойство 2. В линейных цепях новых гармонических составляющих не
возникает.
Рассмотрим линейную цепь вида у = kх. Пусть x(t) = A cosω0t + B cosΩt,
тогда у(t) = kA cos ω0t + kB cos Ωt (рис. 4.22).
4.7. Основные свойства нелинейных цепей
Свойство 1. В нелинейных цепях принцип суперпозиции не
выполняется. В качестве примера нелинейной цепи рассмотрим y = kx2
Если x(t) = x1, то y = y1 = kx12; если x(t) = x2, то y = y2 = kx22;
если x(t) = x1 + x2, то y = kx12 + kx22 + 2kx1x2.
Слагаемое 2kx1x2 возникает в результате взаимодействия двух сигналов
в нелинейной цепи. Его называют комбинационной составляющей.
Свойство 2. В нелинейных цепях происходит трансформация спектра,
т.е. появляются новые гармонические составляющие. Рассмотрим пример
y = kx2 . Пусть x(t) = A cos ω0t + B cosΩt
kA2 kB 2 kA2
kB 2
y kx kA cos 0t kB cos t 2kAB cos 0t cos t
cos2 0t
cos2 0t
2
2
2
2
2
kAB cos 0 t kAB cos 0 t.
2
2
2
2
2

3. Основные режимы работы электрических цепей

• Большинство электрических цепей предназначено для передачи энергии
(сигнала) от источника сигнала в нагрузку.
• 1. В зависимости от характера входного
сигнала:
1. режим постоянного тока;
2. режим гармонического тока ;
3. режим произвольного тока.
2. В зависимости от характера электромагнитных
процессов протекающих в цепи различают два режима работы:
1. установившийся (стационарный) режим, когда параметры сигналов остаются
постоянными во времени величинами;
2. нестационарный или неустановившейся режим, когда параметры сигнала
изменяются во времени. Частый случай - переходной режим.
• 3. В зависимости от нагрузки различают четыре основных режима работы:
1. номинальный. При номинальном режиме все устройства данной цепи
работают в нормальных, установленных изготовителем, условиях.
2. согласованный. Согласованным называют режим передачи от источника к
приемнику наибольшего количества энергии или режим выделения в нагрузке
наибольшей мощности.
Rн
3. холостого хода. Режим холостого хода возникает при отключении
Rн 0 нагрузки,
при обрывах цепи
.
4. короткого замыкания. Режим короткого замыкания, когда
.
3

4. Эквивалентные преобразования электрических цепей

• Цепи называют эквивалентными если при их взаимной замене входные и выходные
токи и напряжения не изменяются.
• Обычно эквивалентные преобразования выполняют с целью упрощения схемы
(уменьшения числа элементов в ней), что в дальнейшем упрощает расчет.
• Правила преобразования зависят от способа соединения элементов.
• Существуют пять способов соединения электрических элементов:
последовательное соединение
параллельное соединение
соединение элементов звездой
соединение элементов треугольником
смешанное соединение
• Электрические цепи считают простыми, если они содержат только последовательное
или только параллельное соединение элементов.
• Цепи (участок цепи), содержащий и параллельное, и последовательное соединение
элементов называют сложными или цепями (участком) со смешанным соединением
элементов.
4

5. 4.3.1. Эквивалентные преобразование схемы

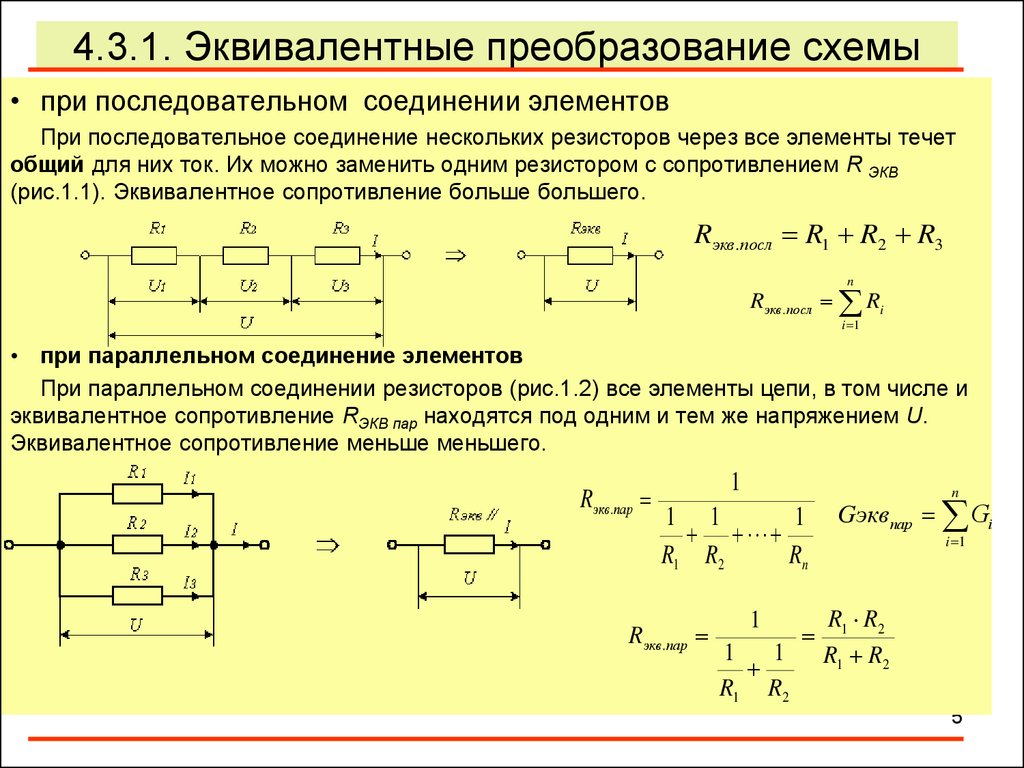
• при последовательном соединении элементов
При последовательное соединение нескольких резисторов через все элементы течет
общий для них ток. Их можно заменить одним резистором с сопротивлением R ЭКВ
(рис.1.1). Эквивалентное сопротивление больше большего.
Rэкв .посл R1 R2 R3
n
Rэкв .посл Ri
i 1
• при параллельном соединение элементов
При параллельном соединении резисторов (рис.1.2) все элементы цепи, в том числе и
эквивалентное сопротивление RЭКВ пар находятся под одним и тем же напряжением U.
Эквивалентное сопротивление меньше меньшего.
Rэкв .пар
1
n
1 1
1
R1 R2
Rn
Rэкв .пар
1
1
1
R1 R2
Gэквпар Gi
i 1
R1 R2
R1 R2
5

6. 4.3.1. Эквивалентные преобразование схемы

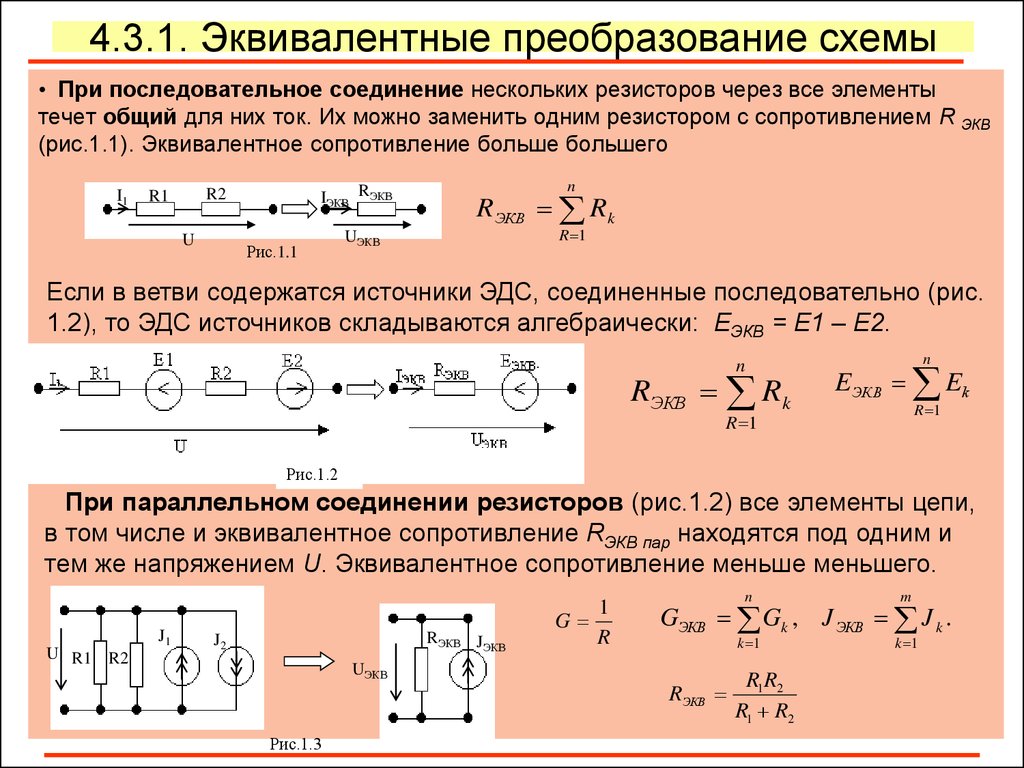
• При последовательное соединение нескольких резисторов через все элементы
течет общий для них ток. Их можно заменить одним резистором с сопротивлением R ЭКВ
(рис.1.1). Эквивалентное сопротивление больше большего
I1
IЭКВ RЭКВ
R2
R1
U
Рис.1.1
n
RЭКВ Rk
R 1
UЭКВ
Если в ветви содержатся источники ЭДС, соединенные последовательно (рис.
1.2), то ЭДС источников складываются алгебраически: EЭКВ = E1 – E2.
n
RЭКВ Rk
n
EЭКВ Ek
R 1
R 1
Рис.1.2
При параллельном соединении резисторов (рис.1.2) все элементы цепи,
в том числе и эквивалентное сопротивление RЭКВ пар находятся под одним и
тем же напряжением U. Эквивалентное сопротивление меньше меньшего.
U R1 R2
J1
RЭКВ J
ЭКВ
J2
UЭКВ
Рис.1.3
1
G
R
n
m
k 1
k 1
GЭКВ Gk , J ЭКВ J k .
RЭКВ
R1R2
R1 R2
6

7. 1.4. ЭКВИВАЛЕНТНОЕ ПРЕОБРАЗОВАНИЕ СХЕМЫ ПРИ СМЕШАННОМ СОЕДИНЕНИИ РЕЗИСТОРОВ

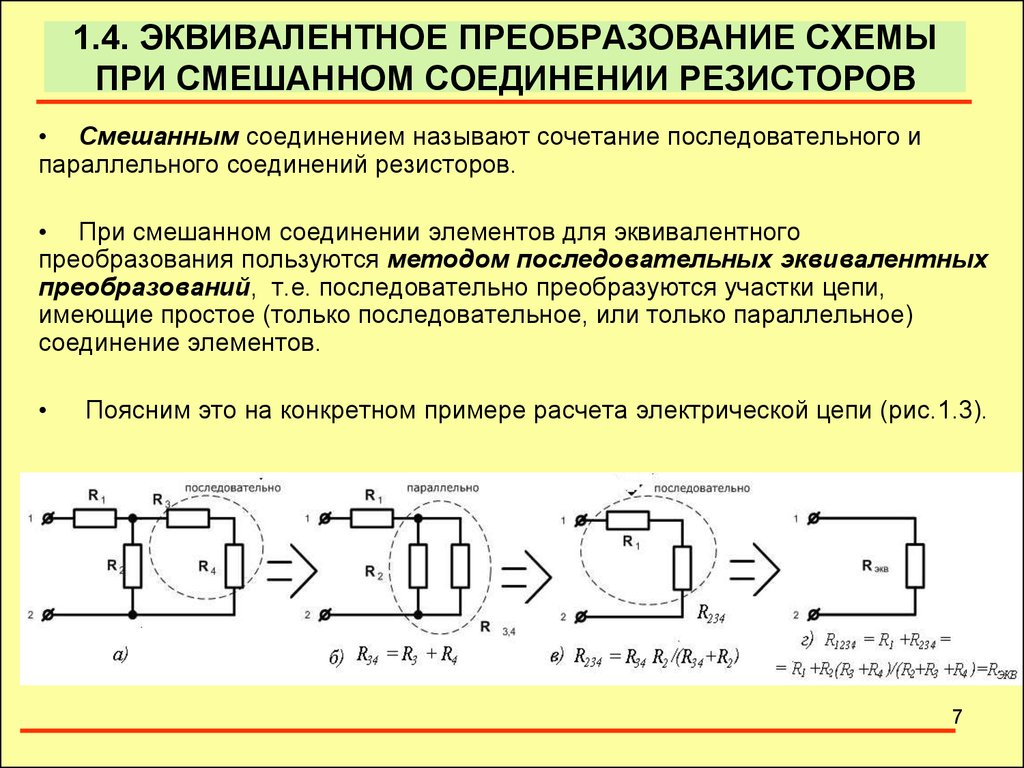
• Смешанным соединением называют сочетание последовательного и
параллельного соединений резисторов.
• При смешанном соединении элементов для эквивалентного
преобразования пользуются методом последовательных эквивалентных
преобразований, т.е. последовательно преобразуются участки цепи,
имеющие простое (только последовательное, или только параллельное)
соединение элементов.
Поясним это на конкретном примере расчета электрической цепи (рис.1.3).
7

8. 1.5. Преобразование соединений треугольник и звезда

Иногда встречаются такие соединения нескольких элементов электрической
цепи, в которых нет возможности выделить последовательное или параллельное
соединение. Например схема мостовой цепи (рисунок ниже).
В таких случаях необходимо выполнить преобразование элементов
соединенных по схеме звезда или треугольник. Это преобразование само по
себе не является упрощением схемы (количество элементов цепи не меняется),
однако приводит схему к виду в котором уже можно выделить последовательные
или параллельные соединения элементов, а следовательно, упростить
последующими преобразованиями.
8

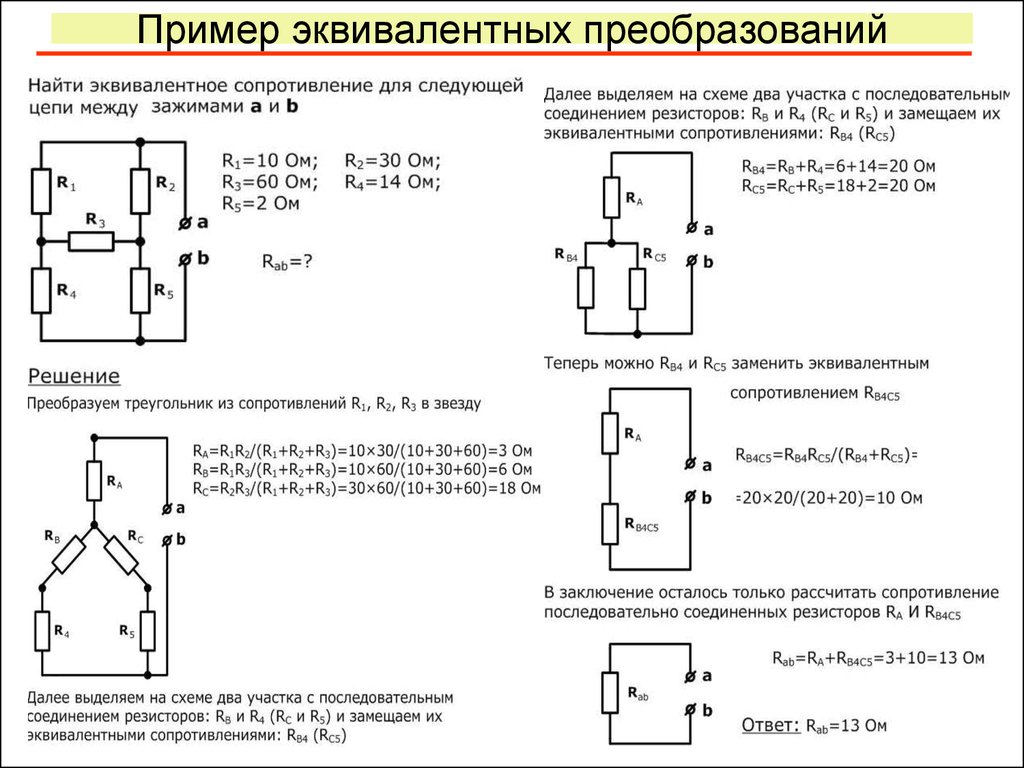
9. Пример эквивалентных преобразований

9

10. 1.6. Эквивалентные преобразования источников

Любой источник можно представить одной из
двух схем.
Схему 1 можно заменить схемой 2, если
параметры схемы 2 выбраны из условий:
I= E/ Rвнu, а Rвнi = Rвнu
Схему 2 можно заменить схемой 1, если
параметры схемы 1 выбраны из условий:
E =I Rвнi, а Rвнu = Rвнi.
Схема 1.
Схема 2
3. При последовательном соединении идеальных источников ЭДС их эквивалентное
ЭДС равно алгебраической сумме ЭДС источников ЭДС.
4. Параллельное соединение источников идеальных ЭДС недопустимо.
5. При параллельном соединении идеальных источников тока их эквивалентный ток
равен алгебраической сумме токов источников тока.
6. Последовательное соединение источников тока недопустимо.
10

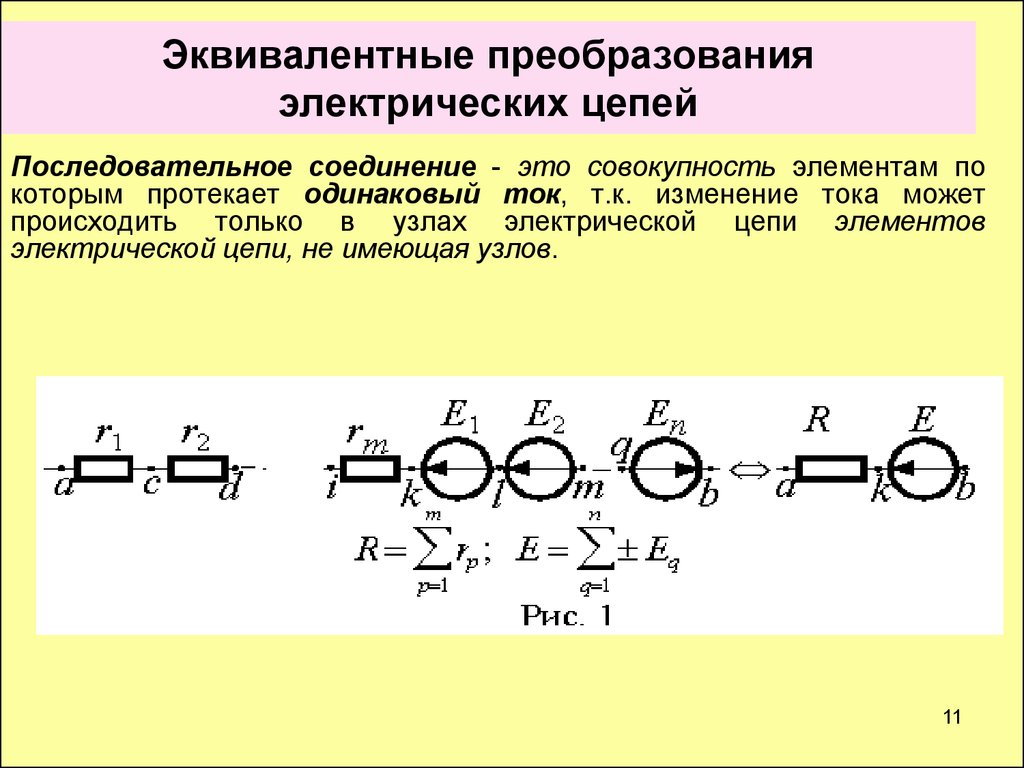
11. Эквивалентные преобразования электрических цепей

Последовательное соединение - это совокупность элементам по
которым протекает одинаковый ток, т.к. изменение тока может
происходить только в узлах электрической цепи элементов
электрической цепи, не имеющая узлов.
11

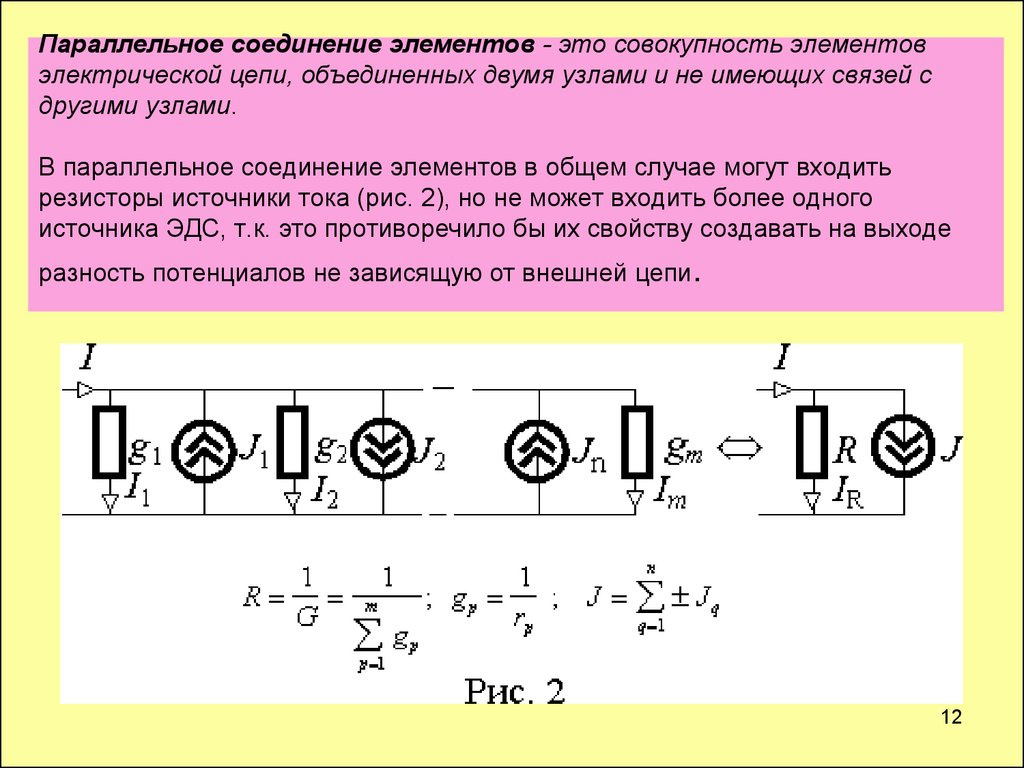
12. Параллельное соединение элементов - это совокупность элементов электрической цепи, объединенных двумя узлами и не имеющих связей с другим

Параллельное соединение элементов - это совокупность элементов
электрической цепи, объединенных двумя узлами и не имеющих связей с
другими узлами.
В параллельное соединение элементов в общем случае могут входить
резисторы источники тока (рис. 2), но не может входить более одного
источника ЭДС, т.к. это противоречило бы их свойству создавать на выходе
разность потенциалов не зависящую от внешней цепи.
12

13.

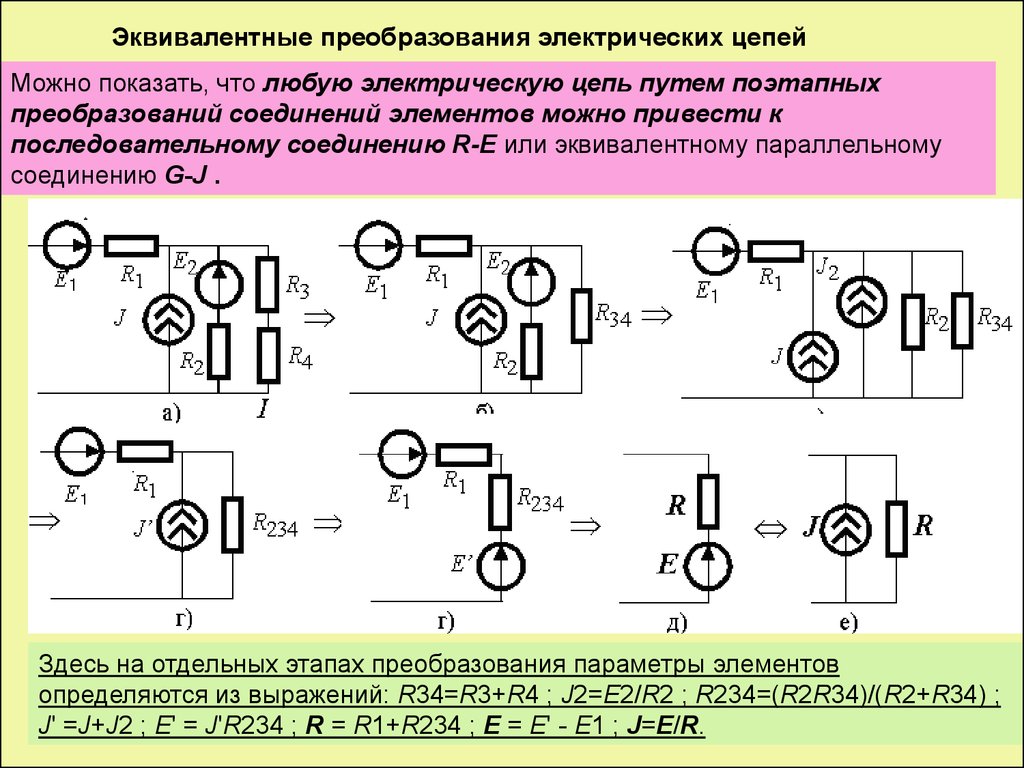
Эквивалентные преобразования электрических цепей
Можно показать, что любую электрическую цепь путем поэтапных
преобразований соединений элементов можно привести к
последовательному соединению R-E или эквивалентному параллельному
соединению G-J .
Здесь на отдельных этапах преобразования параметры элементов
определяются из выражений: R34=R3+R4 ; J2=E2/R2 ; R234=(R2R34)/(R2+R34) ;
13
J' =J+J2 ; E' = J'R234 ; R = R1+R234 ; E = E' - E1 ; J=E/R.

14. Методы расчета цепей постоянного тока

• Под расчетом цепи, в общем случае, понимают нахождение токов
во всех ветвях схемы.
– Основные методы расчета:
1. Метод токов ветвей.
2. Метод контурных токов.
3. Метод узловых напряжений.
4. Метод наложения.
5. Метод эквивалентных преобразований.
14

15. Метод токов ветвей

• В общем случае токи сложной электрической цепи могут быть
определены в результате совместного решения уравнений,
составленных по первому и второму законам Кирхгофа.. Для
однозначного нахождения всех токов необходимо составить в
уравнений.
• Последовательность расчета следующая:
• 1. Проводят топологический анализ схемы.
a11 x1 a12 x2 ... a1N xN в1;
a x a x ... a x в ;
21 1 22 2
2N N
2
............................................
aN 1 x1 aN 2 x2 ... aNN xN вN .
a11
• 1.1. обозначают токи во всех ветвях (I1, I2, …,Iв), произвольно выбирают их
a
положительное направление и обозначают на схеме стрелками;
xi i 21
...
• 1.2. подсчитывают общее число узлов у и число независимых узлов Nу=у-1 и
показывают их на схеме;
an1
• 1.3. подсчитывают число независимых контуров Nk = в-у+1, и показывают их
на схеме дугой.
a12
..... a1n
a22
..... a2 n
...
...
an 2
..... ann
• 2. По первому закону Кирхгофа для независимых узлов и по
второму закону Кирхгофа для независимых контуров
;
относительно токов ветвей записывают уравнения.
• После приведения подобных членов они сводятся к системе линейных
алгебраических уравнений (ЛАУ), где xi =Ii– искомые токи ветвей; aji –
постоянные коэффициенты, зависящие от параметров пассивных элементов
схемы; вi – постоянные величины, зависящие от параметров активных элементов
схемы.
• 3. Решают систему из в уравнений относительно токов, по
методу Крамера и находят токи во всех ветвях схемы. Если
значения некоторых токов отрицательные, то действительные направления их
будут противоположны первоначально выбранным направлениям. I1
• где – главный определитель системы; i – определитель, получается из
главного путем замены i-го столбца на столбец свободных членов вi.
• Пример. Для электрической цепи рис. 1.1 n = 2, m = 3 и расчет токов
цепи осуществляется путем решения следующей системы уравнений
...
I1 I 2 I 3 0
R1I1 R2 I 2 E1 E2
R2 I 2 R3 R4 I 3 E2 E3 E4
15

16. Метод контурных токов

• Метод основан на 2-м законе Кирхгофа. При его использовании в составе
анализируемой схемы выбирают независимые контуры и предполагают, что в каждом из контуров течет свой
контурный ток. Для каждого из независимых контуров составляют уравнение по 2-му закону Кирхгофа и их
решают. Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих по данной ветви.
• Предварительно: Все источники сигналов, представленные источниками
тока, заменяют источниками ЭДС (рис. 4.29).
• 1) Топологический анализ схемы.
а) E = I.ZiI; б) Zu = Zi
а) Как и в предыдущем методе, определяют число ветвей b, Ветви нумеруют
токами показывают их положительное напрвление. б) Определяют число узлов у.
в) Подсчитывают число независимых контуров Nk = b – y + 1 и независимые
контуры обозначены дугами со стрелками на них, которые показывают
положительное направление обхода.
Z11I k1 Z12 I k 2 ... Z1n I kn E11;
Все контуры нумеруют, каждому контуру присваивают свой контурный ток:
Ik1; Ik2; IkNk и выбирают положительное направление контурного тока .
Z 21I k1 Z 22 I k 2 ... Z 2 n I kn E22 ;
• 2) По второму закону Кирхгофа относительно контурных токов
......................................................
записывают уравнения, которые после приведения подобных членов
образуют систему линейных уравнений N = Nk порядка:
• где Iki – контурный ток i-го контура; Zii – собственное сопротивление i-го Z n1I k 1 Z n 2 I k 2 ... Z nn I kn
контура и равно алгебраической сумме сопротивлений,. входящих в i-й контур;
• Zji – сопротивление смежных ветвей между i-м и j-м контурами. Оно берется
со знаком «+», если контурные токи направлены одинаково, и со знаком «–», если
они направлены встречно;
I Кi i
• Eki – контурная ЭДС i-ого контура. Она равна алгебраической сумме ЭДС,
входящих в i-й контур. Контурная ЭДС Eki берется со знаком «+», когда
направление источника ЭДС и направление тока совпадают, и со знаком «–», если
они направлены встречно.
• 3) По правилу Крамера находят контурные токи Iki=.
• 4) Находят токи в ветвяхт как алгебраическую сумму контурных токов,
протекающих через данную ветвь. В алгебраической сумме контурные токи
берутся со знаком «+» , если ток ветви и совпадает с контурным током и «–» если
не совпадает.
• Если токи ветви оказались положительными, то выбранное направление тока
совпадает с истинным и наоборот.
Enn .
n
I n I кi
к 1
16

17. Метод контурных токов (пример)

Последовательность расчета:
• 1) Топологический анализ.
Число ветвей в=3.
Число узлов у=2, число независимых узлов Nу=2-1=1.
Число независимых контуров Nk = b – y + 1= 3-2+1=2..
произвольно выбирают направление условно
действующего контурного тока Iк1, Iк2;
• 2) Составим систему уравнений по методу контурных
токов
Z11I k1 Z12 I
k2
E11;
Z 21I k1 Z 22 I k 2 E22 .
где Z11=R1+R2, Z12=Z21=-R2, Z22=R3+R4,
E11=E1-Е2, E22=E2 - E3+E4.
• 3) решая полученную систему уравнений, находят
контурные токи;
• 4) действительные токи ветвей определяются
алгебраическим суммированием контурных токов,
протекающих в них.
I1 = Ik1; I2 = Ik2 – Ik1; I3 = Ik2.
R1 R2 I k1 R2 I k 2 E1 E2 ;
R2 I k1 R2 R3 R4 I k 2 E2 E3 E4 ;
1
2
I k1 ; I k 2
17

18. Метод узловых напряжений

Метод основан на применении первого закона Кирхгофа. В нем
за неизвестные величины принимают потенциалы узлов. Токи во
всех ветвях схемы определяют по закону Ома
Предварительно: Все источники ЭДС в схеме, заменяют
источниками тока.
а) I = E/ZiI; б) ZiII = ZiI.
1) Топологический анализ.
а) Подсчитывают число ветвей b и число узлов y. Определяется
количество независимых узлов Ny = y – 1.
Y11 1 Y12 2 ... Y1N N I11;
Y Y ... Y I ;
б) Нумеруют все узлы. Один из узлов, к которому сходится
21 1 22 12
2N N
22
наибольшее число ветвей, считают нулевым, где 0=0 –
потенциал нулевого узла.
....................................................
2) По 1-му закону Кирхгофа составляют уравнения для N
YN 1 11 YN 2 2 ... YNN N I NN .
узлов схемы и решают их относительно потенциалов узлов:
где
I – потенциалы узлов,
Yii – собственная узловая проводимость. Она равна сумме
проводимостей всех ветвей, сходящихся в i-м узле, все со знаком
«+»;
Yij – межузловая проводимость между i-м и j-м узлами.
Проводимости всех узлов берутся со знаком «–»;
Iii – алгебраическая сумма токов источников тока, сходящихся в
i-м узле. Втекающие токи записываются в эту сумму со знаком
«+», а вытекающие – со знаком «–».
3) Потенциалы узлов находят по формуле Крамера i=
.
4) Токи в ветвях находят по закону Ома: I = ( 1 – 2)/Z.
i
i
Y11 Y12
Y
Y22
21
YN 1 YN 2
Y1N
Y2 N
YNN
18

19. Метод наложения

,
,
,
Метод наложения
• Метод наложения основан на принципе наложения, согласно которому в линейной
электрической цепи, содержащей несколько источников питания, токи ветвей рассматривают
как алгебраическую сумму токов, вызываемых в этих ветвях действием каждого источника
ЭДС в отдельности.
• Последовательность расчета:
• 1) в цепи поочередно оставляют по одному источнику питания и получают расчетные
схемы, число которых равно числу источников питания (внутренние сопротивления
исключенных источников оставляют в цепи);
• 2) определяют токи всех ветвей расчетных схем, используя методы преобразования
цепей;
• 3) действительные токи ветвей находят суммированием (наложением) соответствующих
токов расчетных схем с учетом их направлений.
• Эффективен этот метод для расчета цепей, содержащих небольшое число источников.
Пример1. Рассчитать методом наложения токи в ветвях для схемы на рис. 1.1
1. Составим расчетные
схемы а и б
I11
E
1
R123
I 22
E
2
R321
I 21
1
U da
R2
I 22
2. Найдем первый, второй и третий частичные токи от первого источника.
Найдем первый, второй и третий частичные токи от второго источника
3. Найдем токи в ветвях
I1 I11 I12
I 2 I 21 I 22
I31
1
U da
R3
2
2
U da
U
2
da
I3
R2
R3
I3 I31 I32
19

20. Метод двух узлов

• Метод двух узлов применяется для расчета цепей,
имеющих только два узла. Сущность метода
заключается в определении напряжения между
узлами, после чего токи ветвей находят по
обобщенному закону Ома.
• Порядок расчета:
1) произвольно выбирают направление узлового
напряжения Uab и определяют его величину по
формуле (1),
где n g k Ek – алгебраическая сумма произведений
ЭДС1 и проводимостей каждой ветви (gkEk берут со
знаком плюс, если направление ЭДС Ek
противоположно направлению напряжения Uab и со
знаком минус, когда их направления совпадают);
• m g k – сумма проводимостей всех ветвей цепи.
n
U ab
gk Ek
1
m
gk
(1)
1
1
Например, для цепи рис. 1.1 узловое напряжение
Uab равно
2) токи в ветвях рассчитывают по обобщенному
закону Ома
U ab
1
1
1
E1
E2
( E3 E 4 )
R1
R2
R3 R4
1
1
1
R1 R2 R3 R4
20

21. Метод эквивалентного генератора

•Метод эквивалентного генератора применяется в тех
случаях, когда требуется определить ток только в одной ветви
сложной цепи. При этом выделяют расчетную ветвь (или
участок ветви), а всю остальную часть цепи заменяют
эквивалентным генератором с ЭДС Еэ и внутренним
сопротивлением Rэ.
Eэ
•Например, для расчета тока I3 в цепи рис. 1.1 эквивалентная
I3
замена показана на рис.1.2., тогда I3 =
Rэ R3
•Параметры эквивалентного генератора Еэ , Rэ определяются
аналитически, либо экспериментально.
•1. ЭДС Еэ равна напряжению на разомкнутых зажимах
расчетной ветви (напряжению холостого хода) Uае.х
(рис.1.3а) и может быть рассчитана или измерена
вольтметром. Так, аналитически напряжение Uае.х в цепи
рис. 1.3а выражается уравнением
E E
•Еэ =Uае.х = Е1– Е3+ Е4–R1Iх , где
Ix
1
2
R1 R2
•Внутреннее
сопротивление
Rэ
равно
входному
сопротивлению цепи Rвх по отношению к зажимам
выделенной ветви (участка).
•Для расчета Rвх все источники ЭДС-закорачивают, а
источники токазаменябт разрывом цепи и подсчитывают экв.
относительно зажимов ае (рис. 1.3б). Rвх =
•Оно может быть измерено косвенно, как Rвх = Uае.х / I3к, где
I3к – ток расчетной ветви при коротком замыкании
выделенного участка ае.
•Тогда искомый ток I3=
Rвх
R1 R2
R4
R1 R2
I3
U ае.х
Rвх R3
21