Similar presentations:
Электрические цепи постоянного тока. Методы анализа линейных электрических цепей постоянного тока
1. Электрические цепи постоянного тока
Методы анализа линейныхэлектрических цепей постоянного
тока
2. Метод контурных токов
Метод контурных токов сводится ксоставлению и решению системы
уравнений, получаемых по второму
закону Кирхгофа применительно к
понятиям контурных токов,
сопротивлений и ЭДС
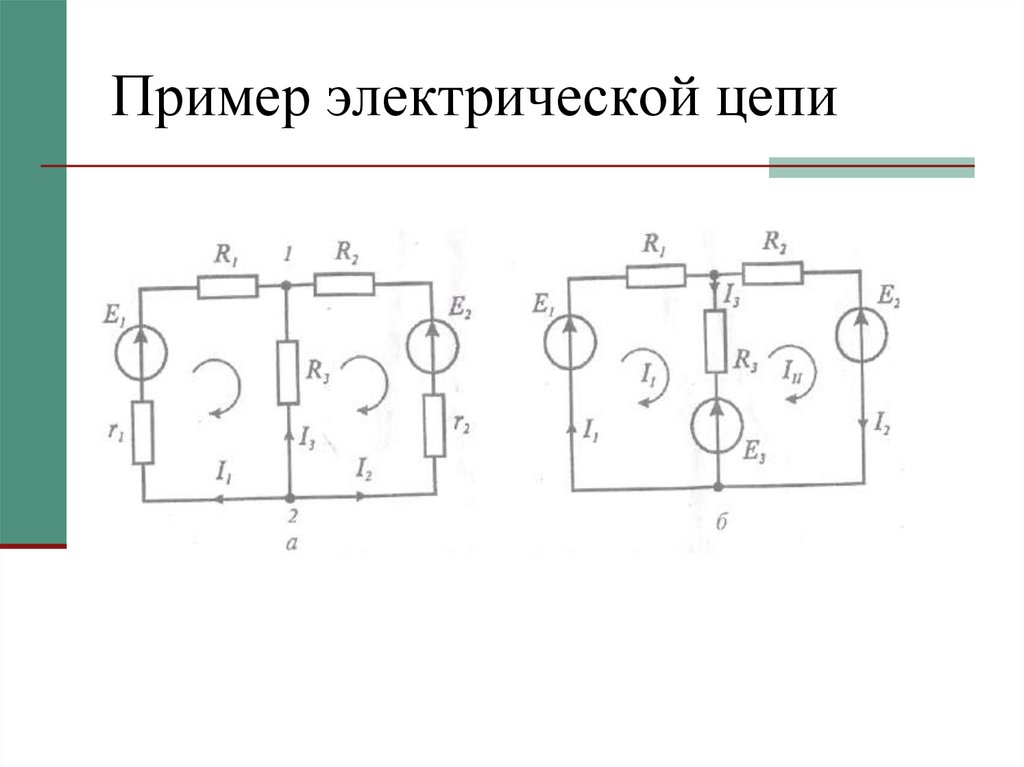
3. Пример электрической цепи
4. Система уравнений для данной цепи по законам Кирхгофа
I1 - I2 - Iз = 0;R1I1 + R3 I3 = E1 – E3;
R2I2 - R3 I3 = E3 – E2.
Подставим I
других:
3
из первого уравнения в два
5. Система контурных токов для данной цепи
R11II + R12III = EI;R21II + R22III = EII,
где контурные ЭДС: EI
= E1 – E3;
ЕII = Е3 - Е2;
II , III - контурные
токи;
II=I1; III =I2
I3 = II - III
Собственные
Сопротивления
контуров:
R11=R1+R3;
R22=R2 + R3.
Взаимное
сопротивление
контуров:
R12 = R21 = — R3
6. Система контурных уравнений (Общий случай)
R11 II + R12III +….+ R1к Iк + …+ R1n In = EIR21 II + R22III +….+ R2к Iк + …+ R2n In = EII
–——————————
Rк1 II + Rк2III +….+ Rкк Iк + …+ Rкn In = Eк
–——————————
Rn1 II + Rn2III +….+ Rnк Iк + …+ Rnn In = En,
где Rk— собственные сопротивления k-го
контура;
Rki - взаимные сопротивления k-го и i-го контуров;
Ek - контурная ЭДС k-го контура.
7. Контурный ток
8. Порядок расчета электрических цепей методом контурных токов
выбрать независимые контуры цепи и указатьположительные направления контурных токов Ik;
вычислить собственные Rkk и взаимные Rik
сопротивления контуров, а также контурные ЭДС
Ek;
составить систему уравнений контурных токов по
второму закону Кирхгофа;
решить полученную систему уравнений,
определив контурные токи Ik;
определить токи I1, I2... в ветвях.
9. Рекомендации по применению метода контурных токов
Метод контурных токов целесообразноприменять для расчетов таких цепей, у
которых число независимых контуров не
более числа узлов (п = у).
Если схема содержит источник тока, то
рекомендуется предварительная их
замена эквивалентными источниками ЭДС.
10. Метод наложения (суперпозиции)
Ток в любой ветви линейнойэлектрической цепи, содержащей
несколько источников ЭДС, равен
алгебраической сумме токов в этой
ветви при действии каждого
источника в отдельности.
11. Метод наложения
При этом остальные источникизаменяются резисторами, имеющими
сопротивления, равные внутренним
сопротивлениям замененных источников
ЭДС.
Справедливость этого принципа следует
непосредственно из
12. Метод наложения
Метод наложения позволяет найти токи в ветвяхбез составления и решения системы уравнений, а
непосредственно по закону Ома.
Сначала находят частичные токи от действия
каждого источника ЭДС в отдельности, принимая
остальные ЭДС равными нулю и оставляя в схеме
только их внутренние сопротивления, а затем —
действительные токи как алгебраические суммы
частичных токов.
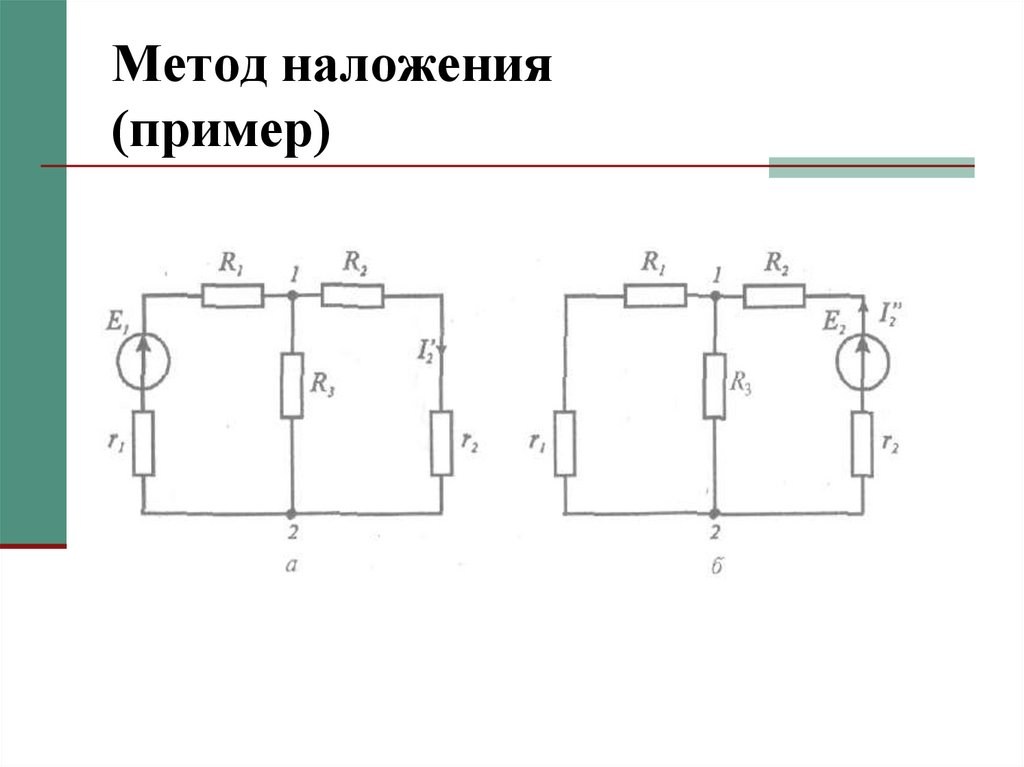
13. Метод наложения (пример)
14. Метод наложения (пример)
Напряжение между точками 1 и 2:Частичный ток в ветви
2 от ЭДС 1:
I2' = U12/(R2+r2)
Действительный ток
Частичный ток от ЭДС 2:
в ветви 2:
I2 = I'2 – I″2
15. Рекомендации по применению метода наложения
Метод наложения удобно применять, когдавспомогательные схемы принимают
простой вид и их расчет не представляет
трудностей.
Применение этого метода
нецелесообразно при расчете схем с
большим числом источников.
16. Метод эквивалентного генератора
Метод эквивалентного генератора основан натеореме об эквивалентном генераторе
напряжения: ток в любой ветви линейной
электрической цепи не изменится, если
остальную часть цепи заменить эквивалентным
источником напряжения, ЭДС которого равна
напряжению на зажимах разомкнутой ветви, а
сопротивление этой части цепи равно
сопротивлению между точками разрыва при
условии, что источники ЭДС и тока заменены их
внутренними сопротивлениями.
17. Метод эквивалентного генератора
Заменив эквивалентный источник напряженияисточником тока, получим эквивалентный
источник тока, для которого справедлива теорема
об эквивалентном генераторе тока.
Метод эквивалентного генератора особенно
удобно применять тогда, когда требуется найти
ток в одной из ветвей электрической цепи. Эта
ветвь рассматривается как нагрузочное
сопротивление, а вся остальная схема — как
эквивалентный генератор.
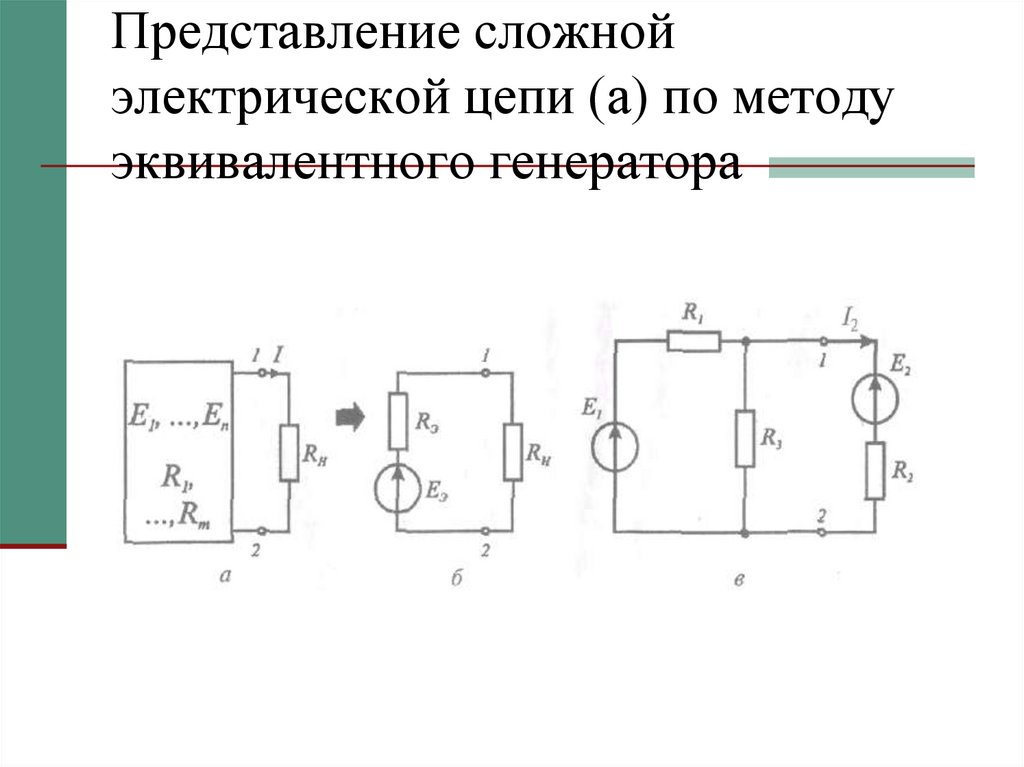
18. Представление сложной электрической цепи (а) по методу эквивалентного генератора
19. Пример определения тока методом эквивалентного генератора
20. Метод узловых потенциалов (напряжений)
Сущность этого метода сводится к решениюсистемы уравнений, составленных по первому
закону Кирхгофа; из этих уравнений определяют
напряжения в узлах схемы электрической цепи
относительно некоторого базисного узла,
потенциал которого принимают равным нулю, а
токи в ветвях, соединяющих узлы, находят по
закону Ома.
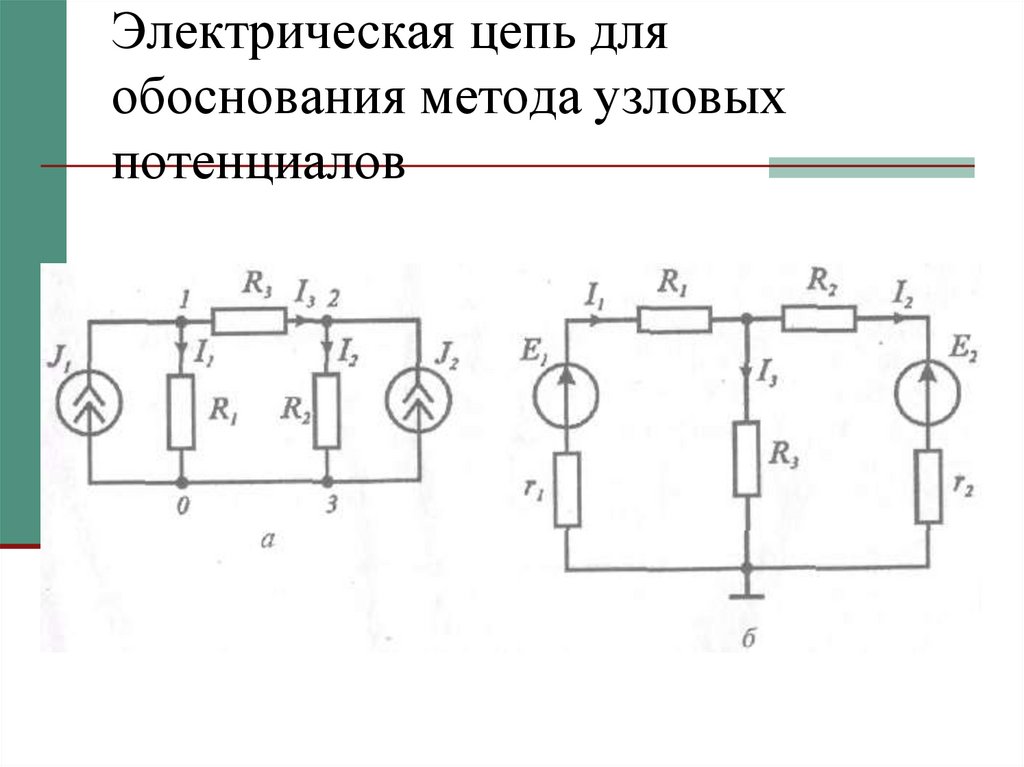
21. Электрическая цепь для обоснования метода узловых потенциалов
22. Уравнения по первому закону Кирхгофа для незаземленных узлов
где g1, = l/R1, g2 = 1/R2; g3 = 1/R3. Так как φ0 = 0, то23. Метод узловых потенциалов
Принимая, g11 = g1 + g3;g22= g2 + g3 и g12 = g2l = g3 получим:
24. Система уравнений для узловых потенциалов электрической цепи с (п + 1) узлами
25. Обозначения в системе уравнений для узловых потенциалов
gnn - собственная проводимость n-го узла, равнаясумме проводимостей всех ветвей, соединенных с
этим узлом
( всегда положительная);
gni — взаимная проводимость между n-м и i-м
узлами, равная сумме проводимостей всех
ветвей, соединяющих эти узлы, если цепь не
содержит зависимых источников электрической
энергии(всегда отрицательная);
26. Узловой ток
Jn — узловой ток n-го узла, равныйалгебраической сумме токов
источников тока, подсоединенных к n
-му узлу; эти токи входят в сумму со
знаком «плюс», если они направлены
к узлу, и со знаком «минус», если
направлены от узла.
27. Пояснения к методу узловых потенциалов
Если в схеме электрической цепи часть источников заданаисточниками ЭДС, то их необходимо заменить
эквивалентными источниками тока.
Это можно сделать, не изменяя схему цепи: оставить в
ветви с источником ЭДС все сопротивления и учесть, что
между узлами этой ветви подсоединен источник тока, у
которого ток равен произведению ЭДС на суммарную
проводимость ветвей.
Решив систему узловых потенциалов, находят потенциалы
узлов, а затем токи в ветвях по закону Ома.
28. Порядок расчета электрической цепи методом узловых потенциалов
принять потенциал одного из узлов равным нулюи пронумеровать по порядку (1, 2, 3, ...) остальные
узлы;
вычислить узловые токи J1, J2, ...;
определить собственные и взаимные
проводимости узлов;
составить и решить систему уравнений узловых
потенциалов;
найти токи в ветвях, пользуясь законом Ома.
29. Пояснения к методу узловых потенциалов
Если какая-нибудь ветвь содержит идеальныйисточник ЭДС и, следовательно, напряжение
между двумя узлами задано, целесообразно в
качестве базисного узла выбрать один из узлов
данной ветви.
В этом случае число неизвестных узловых
напряжений и, стало быть, число узловых
уравнений уменьшится на единицу.
30. Рекомендации по выбору метода метод узловых потенциалов
Если число независимых узлов(у — 1) в схеме цепи меньше числа
независимых контуров, то для ее расчета
целесообразно использовать метод
узловых потенциалов, при этом все
источники ЭДС следует преобразовать в
эквивалентные источники тока.


























 physics
physics








