Линейные электрические цепи. Постоянный ток

1. ЭЛЕКТРО ТЕХНИКА

2.

Вариант контрольного задания определяется двумя
последними цифрами номера зачетки. Если получаемое
число больше 49, то следует для нахождения номера
варианта вычесть 50.
Задание 10.1: пункты 1, 2, 3, 4.
Можно удалить из схемы источники тока.
Задание 10.2: пункты 1, 2, 6.
Ваттметр на схеме указывать не нужно.
Литература
1. Сивяков Б.К. Электротехника и электроника: учеб.
пособие / Б.К. Сивяков, В.С. Джумалиев. Саратов: Сарат. гос.
техн. ун-т, 2009. 116 с.
2. Бессонов Л.А. Теоретические основы электротехники.
Электрические цепи: учебник для вузов / Л.А. Бессонов. М.:
Гардарики, 2009. 638 с.

3. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННЫЙ ТОК

4.

В
теории
электрических
цепей
заменяем
реальное
электромагнитное
устройство
некоторым
расчетным
эквивалентом – электрической цепью.
Электрическая цепь - совокупность соединенных источников и
нагрузок, по которым может протекать электрический ток.
СИЛА ТОКА - I, А
НАПРЯЖЕНИЕ - U, В
ЭДС - E, В
ПОТЕНЦИАЛ - , В
СОПРОТИВЛЕНИЕ - R, Ом
ПРОВОДИМОСТЬ - G=1/R, См
Электрическая схема – изображение электрической цепи с
помощью условных знаков.

5.

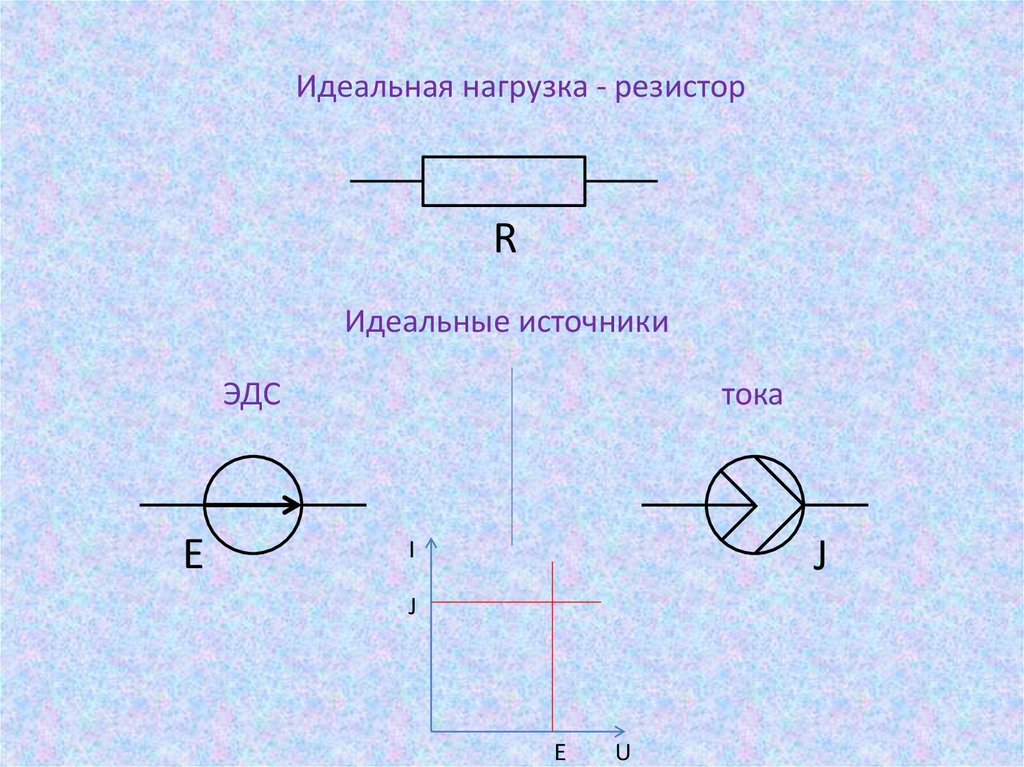
Идеальная нагрузка - резистор
R
Идеальные источники
ЭДС
E
тока
J
I
J
E
U

6.

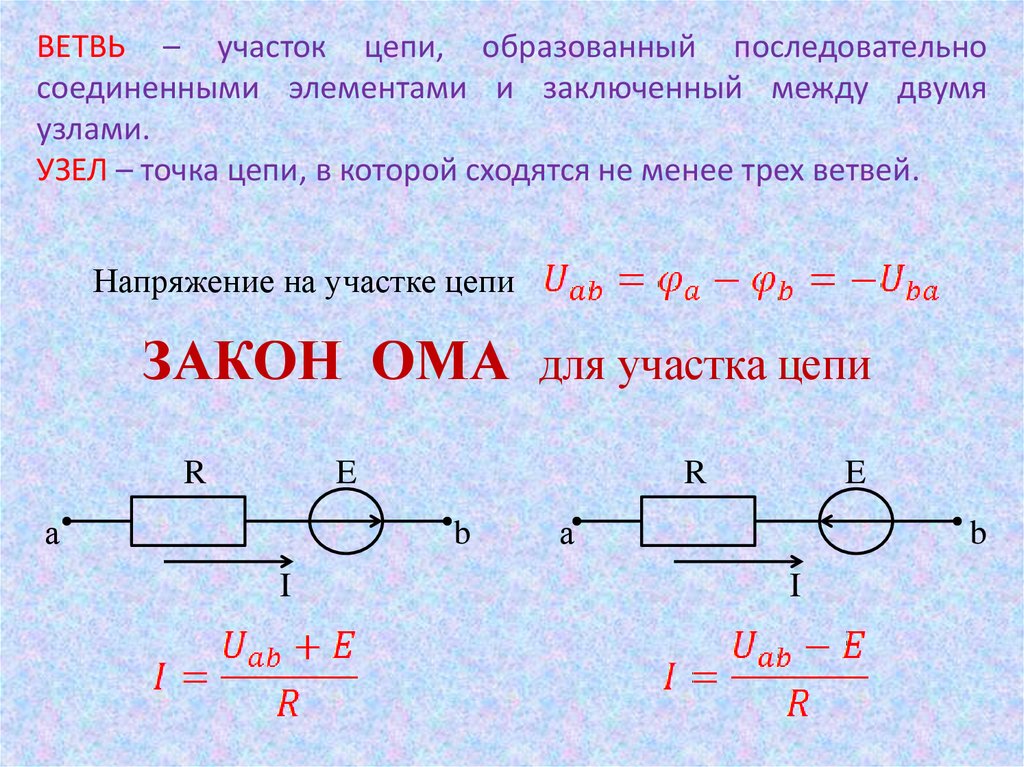
ВЕТВЬ – участок цепи, образованный последовательно
соединенными элементами и заключенный между двумя
узлами.
УЗЕЛ – точка цепи, в которой сходятся не менее трех ветвей.
Напряжение на участке цепи
ЗАКОН ОМА для участка цепи
R
E
а
R
b
I
E
а
b
I

7.

I3
2
I4
R3
R4
R1
1
3
I1
R6
E1 R5
I6
I5
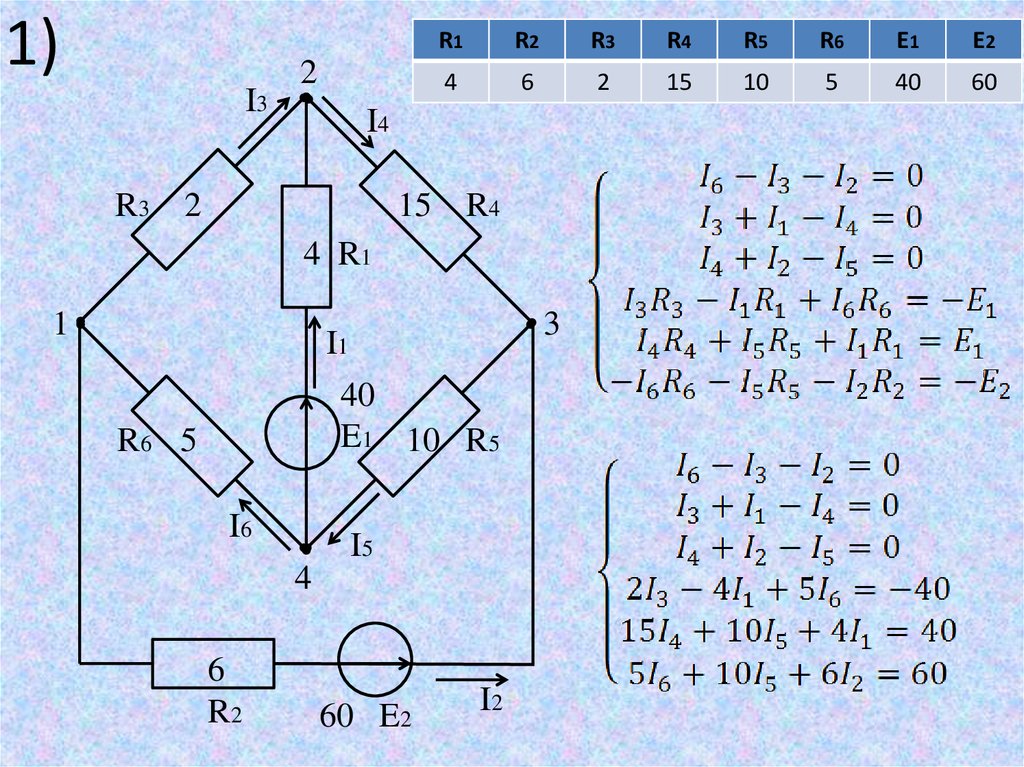
1) Составить уравнения по
правилам Кирхгофа.
Систему не решать.
2) 2. Найти все токи в
ветвях методом
контурных токов.
3) Найти все токи в ветвях
методом узловых
потенциалов.
4) Результаты свести в
таблицу.
4
МКТ
МУП
R2
E2
I2

8. ЗАКОНЫ КИРХГОФА

1. Алгебраическая сумма токов в узле равна
нулю.
2. Алгебраическая сумма падений
напряжений на элементах замкнутого
контура равна алгебраической сумме ЭДС
этого контура.
По правилам Кирхгофа составляем столько уравнений, сколько в
схеме ветвей (неизвестных токов). Из них по первому правилу
составляем уравнений на 1 меньше количества узлов, остальные
уравнения составляем по второму правилу.

9.

1)
I3
R3
2
R1
R2
R3
R4
R5
R6
E1
E2
4
6
2
15
10
5
40
60
I4
2
15
R4
4 R1
1
3
I1
40
E1 10 R5
R6 5
I6
I5
4
6
R2
60 E2
I2

10. МЕТОД КОНТУРНЫХ ТОКОВ

2)
Независимый контур – контур, отличающийся от прочих контуров
хотя бы на одну ветвь.
Предположим, что в каждом независимом контуре течёт свой
контурный ток.
Выберем направления контурных токов по часовой стрелке.
Система уравнений в общем виде для трёх независимых контуров:

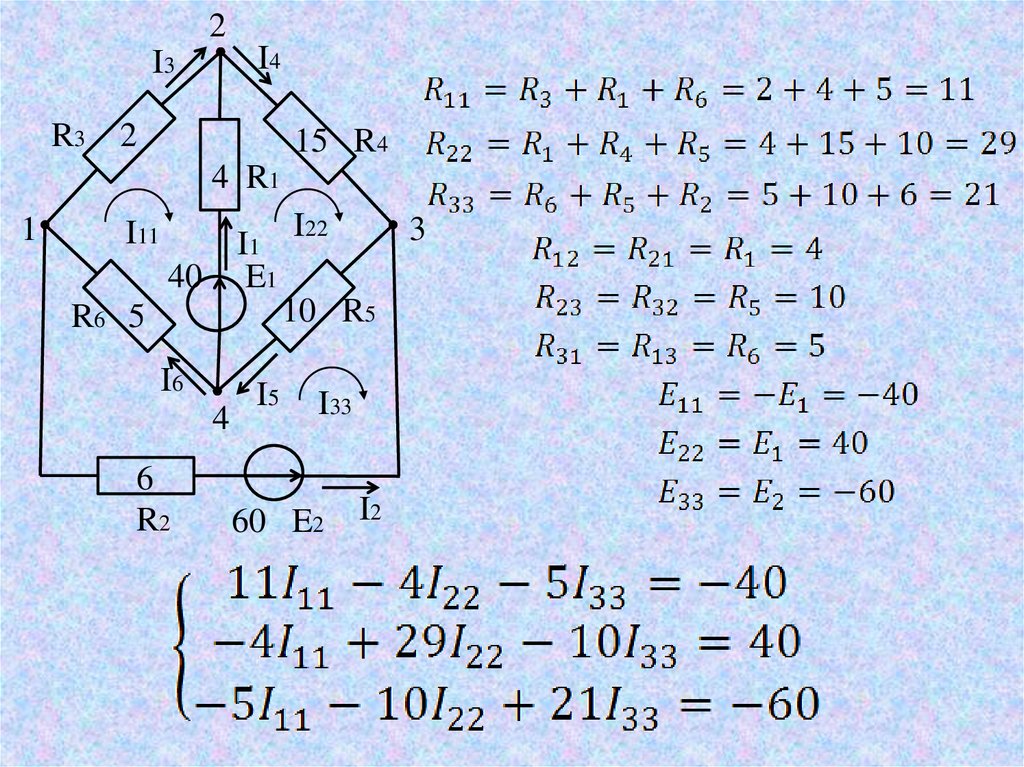
11.

2
I4
I3
R3
2
15 R4
4 R1
1
I11
I1
E1
40
I22
3
10 R5
R6 5
I6
4
6
R2
I5
I33
60 E2
I2

12.

1
2
I4
I3
R3
2
15 R4
4 R1
3
I1 I22
E1
10 R5
I11
40
R6 5
I6
4
6
R2
I5
60 E2
I33
I2
Выразим токи в ветвях
через контурные токи:

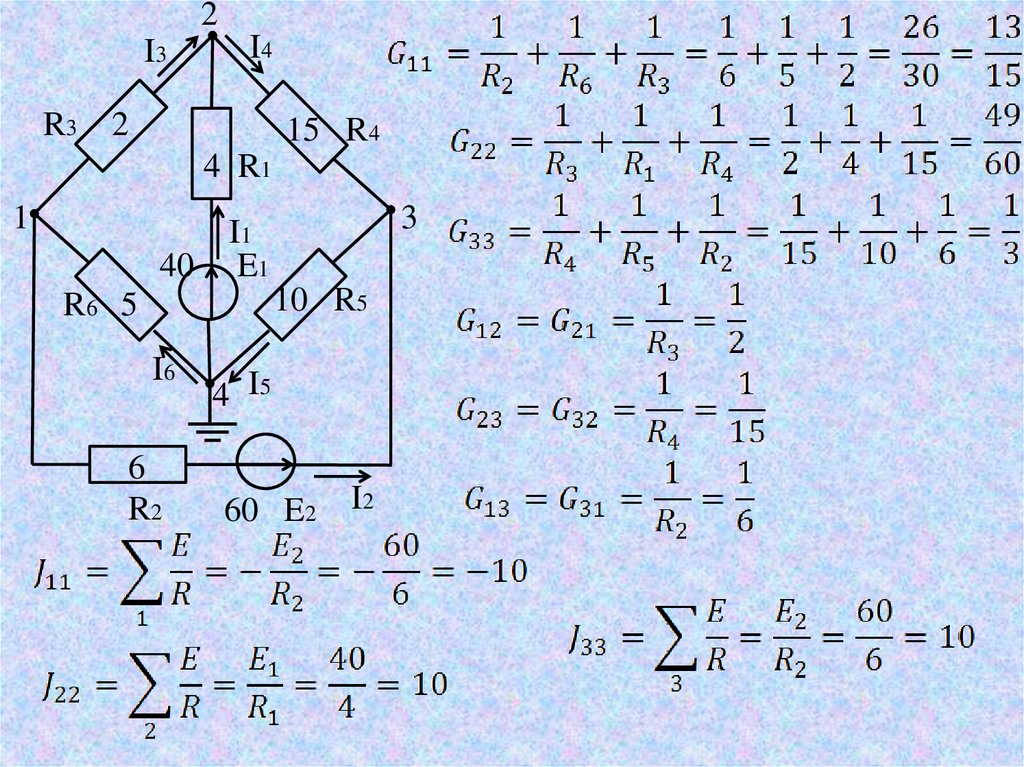
13. МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ

3)
Заземлим один узел
.
Для оставшихся узлов запишем систему уравнений в общем виде:

14.

2
I3
R3
I4
2
15 R4
4 R1
1
40
3
I1
E1
10 R5
R6 5
I6
6
R2
4 I5
60 E2
I2

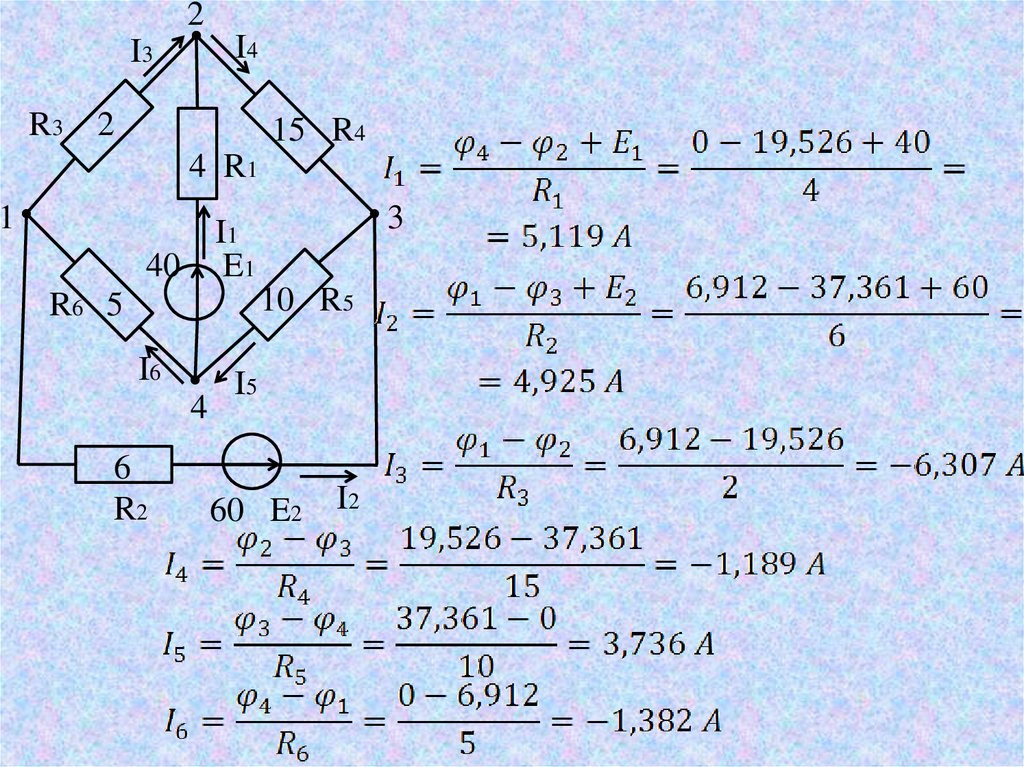
15.

Зная потенциалы, по закону Ома найдём токи в ветвях.

16.

2
I4
I3
R3
2
15 R4
4 R1
1
3
I1
E1
40
10 R5
R6 5
I6
4
6
R2
I5
60 E2
I2

17.

4)
I1
I2
I3
I4
I5
I6
МКТ
5,118
4,925 -6,307 -1,189 3,736 -1,382
МУП
5,119
4,925 -6,307 -1,189 3,736 -1,382

18. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

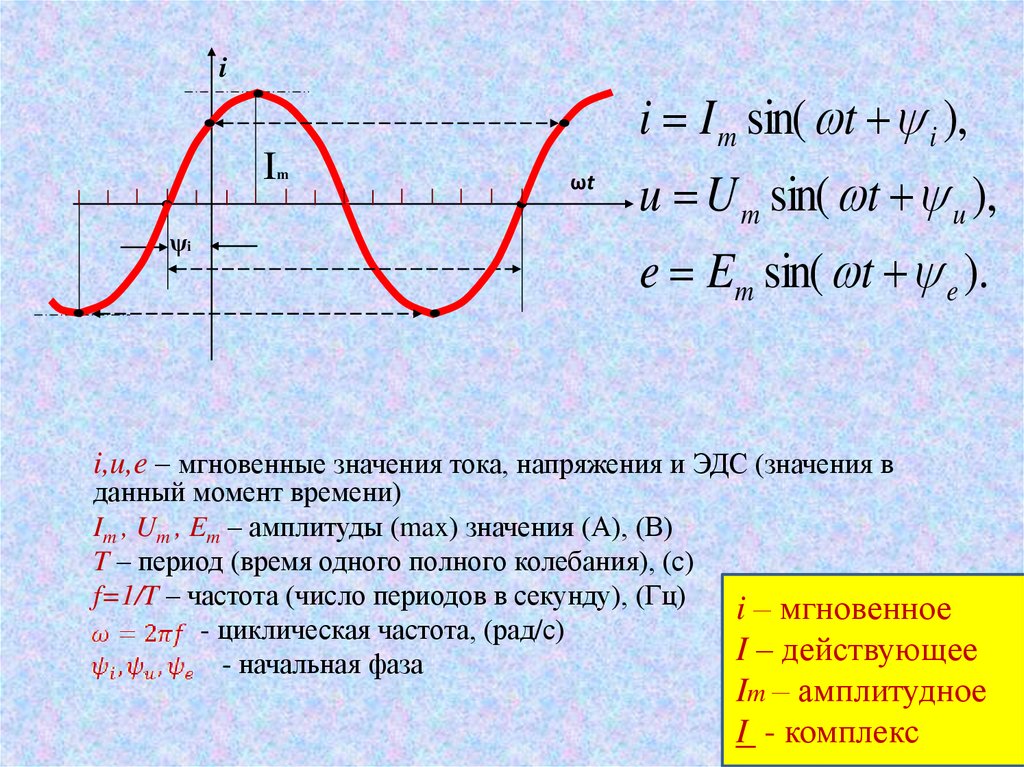
19.

i
I
ψi
i I m sin( t i ),
m
ωt
u U m sin( t u ),
e Em sin( t e ).
i,u,e – мгновенные значения тока, напряжения и ЭДС (значения в
данный момент времени)
Im , Um , Em – амплитуды (max) значения (А), (В)
T – период (время одного полного колебания), (с)
f=1/T – частота (число периодов в секунду), (Гц)
- циклическая частота, (рад/с)
- начальная фаза
i – мгновенное
I – действующее
Im – амплитудное
I - комплекс

20.

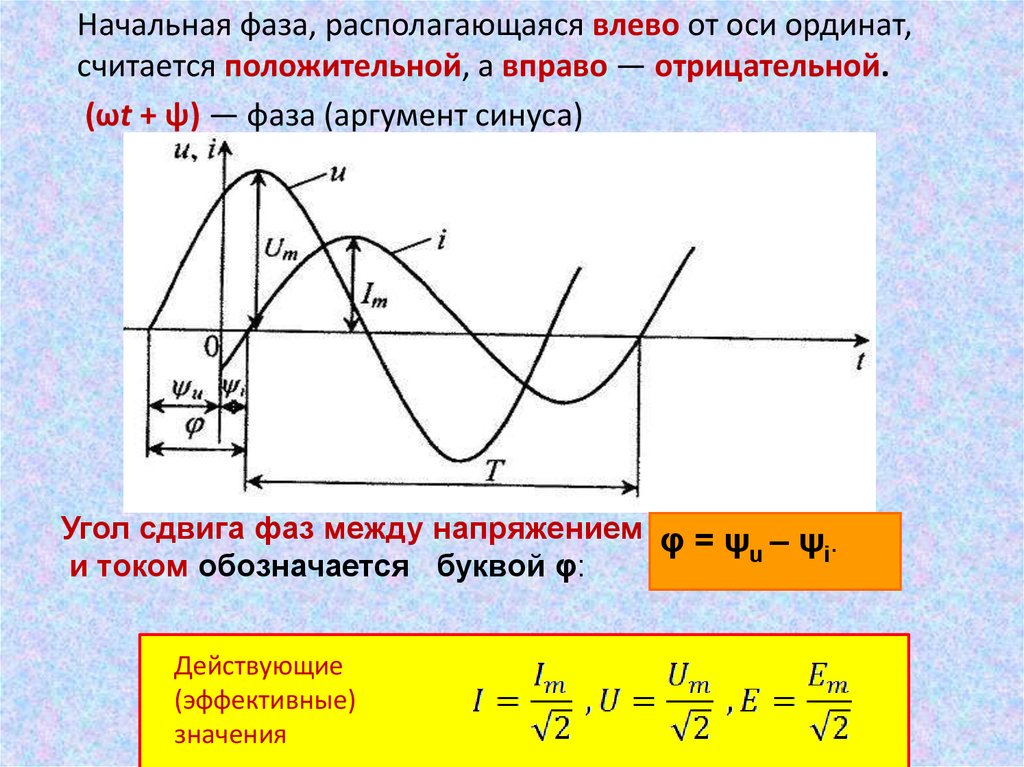
Начальная фаза, располагающаяся влево от оси ординат,
считается положительной, а вправо — отрицательной.
(ωt + ψ) — фаза (аргумент синуса)
Угол сдвига фаз между напряжением φ = ψ – ψ .
u
i
и током обозначается буквой φ:
Действующие
(эффективные)
значения

21. Комплексная плоскость

КОМПЛЕКСНАЯ
ПЛОСКОСТЬ
Im
три формы записи комплексного числа:
- алгебраическая
- показательная (экспоненциальная)
- тригонометрическая
b
a
Re
- модуль комплексного числа
комплексно сопряженное
- его аргумент
ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ
j иногда называют
оператором поворота
Умножение на j поворачивает вектор на угол /2,
умножение на (-j) или
деление на j - на угол (- /2)

22. Основные элементы электрической цепи переменного тока

ОСНОВНЫЕ ЭЛЕМЕНТЫ
ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ПЕРЕМЕННОГО ТОКА
Электрический ток (движение электрических
зарядов) неразрывно связан с магнитным и
электрическим полем.
Основными элементами цепи переменного
тока, помимо источников электроэнергии,
являются резистивные, индуктивные и
емкостные элементы.

23.

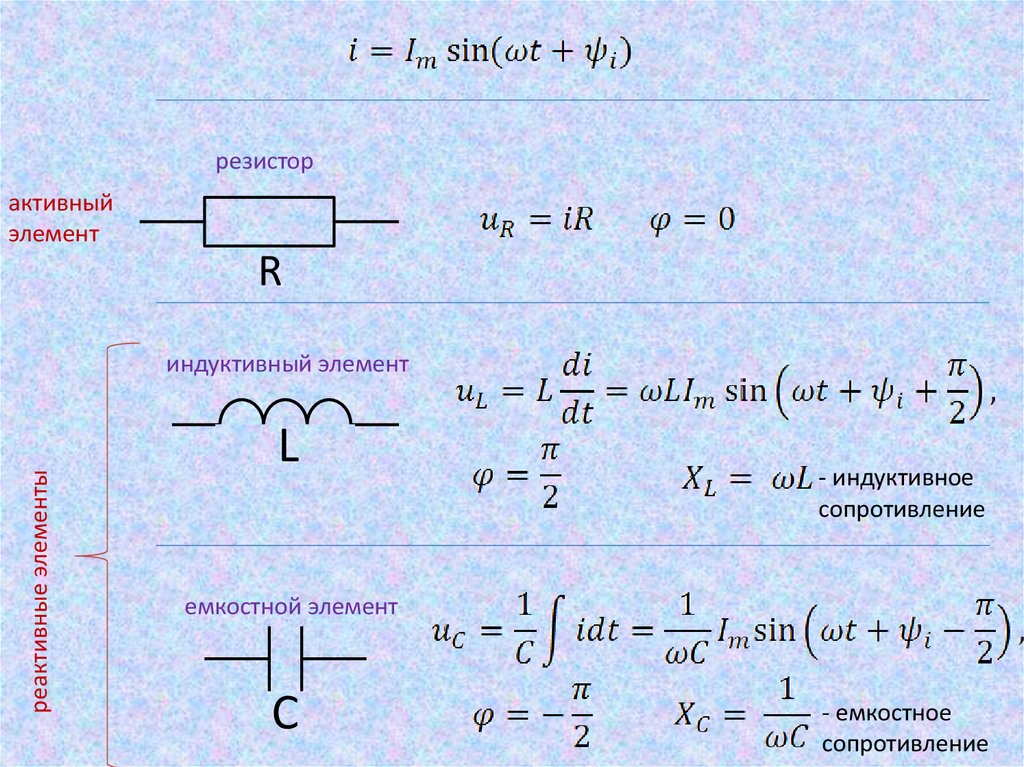
резистор
активный
элемент
R
реактивные элементы
индуктивный элемент
L
- индуктивное
сопротивление
емкостной элемент
С
- емкостное
сопротивление

24.

символический метод
расчёта цепей
синусоидального тока
(комплексный метод)
Любую цепь синусоидального тока можно рассчитывать, как
цепь постоянного тока, если все величины представить в
комплексной форме.
Токи и напряжения заменяют их комплексными
изображениями. При этом дифференциальные уравнения
для мгновенных значений заменяются алгебраическими
уравнениями для комплексов.

25. Последовательный RLC контур

R
i
uR
u
C
L
uL
uC
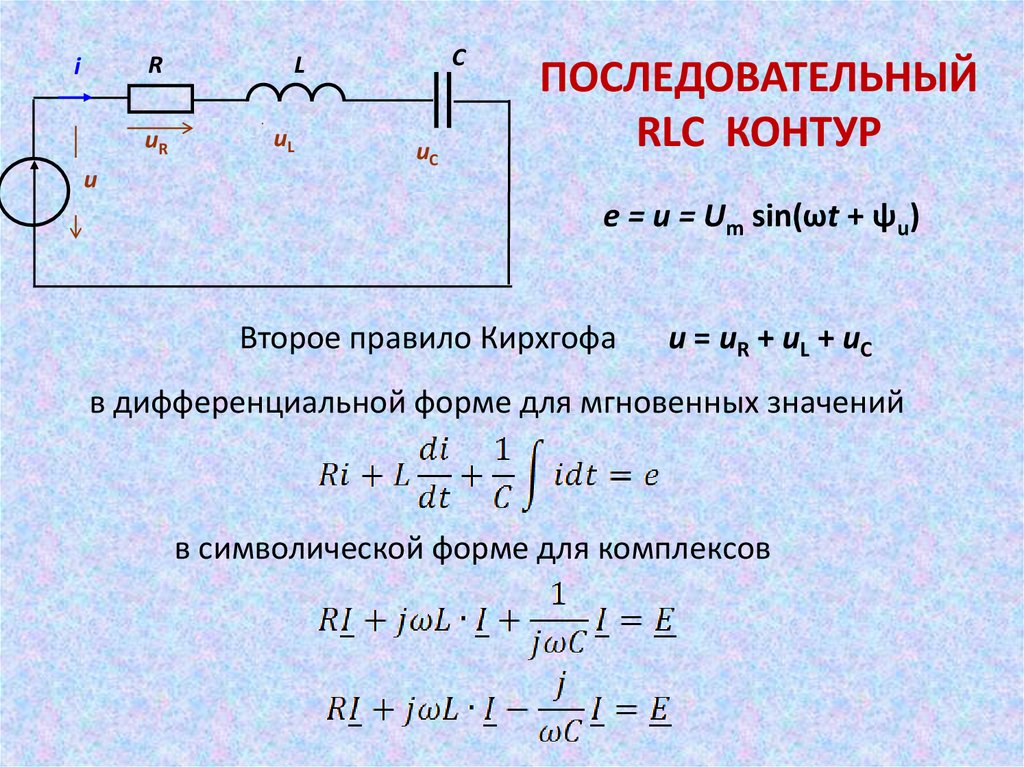
ПОСЛЕДОВАТЕЛЬНЫЙ
RLC КОНТУР
е = u = Um sin(ωt + ψu)
Второе правило Кирхгофа
u = uR + uL + uC
в дифференциальной форме для мгновенных значений
в символической форме для комплексов

26.

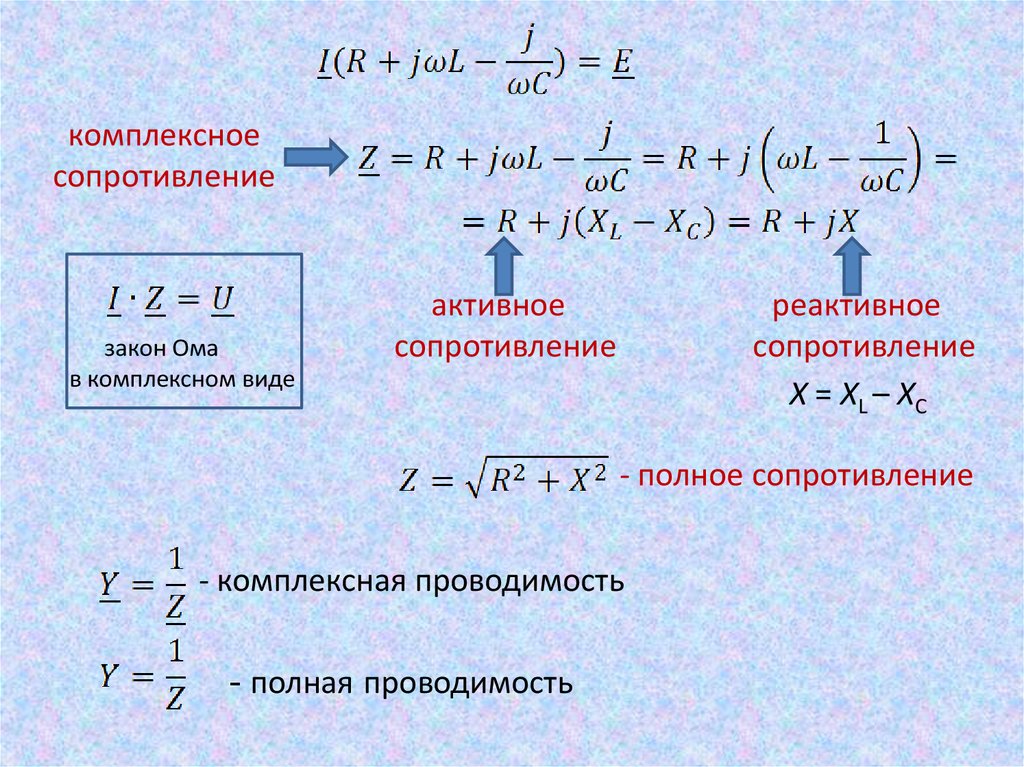
комплексное
сопротивление
закон Ома
в комплексном виде
активное
сопротивление
реактивное
сопротивление
X = XL – X C
- полное сопротивление
- комплексная проводимость
- полная проводимость

27.

e