Сферическое движение ТТ как движение с одной неподвижной точкой

1.

А.И. Родионов
Теоретическая механика.
Ч.1. КИНЕМАТИКА

2.

Лекция 11
Сферическое движение ТТ как движение с одной
неподвижной точкой.
Движения большинства аэро, астро и ряда морских
навигационных приборов, основой которых является
гироскоп,- есть движения с одной неподвижной точкой –
сферическое движение.
Движение ТТ имеющее одну неподвижную точку
называется сферическим , т.к. все точки этого тела
движутся по поверхностям сфер, с центрами ,
находящимися в неподвижной точке.

3.

§11.1. Теорема Эйлера – Даламбера
Твердое тело, имеющее одну неподвижную точку, можно
переместить из одного положения в любое другое одним
поворотом вокруг некоторой оси, проходящей через
неподвижную точку.

4.

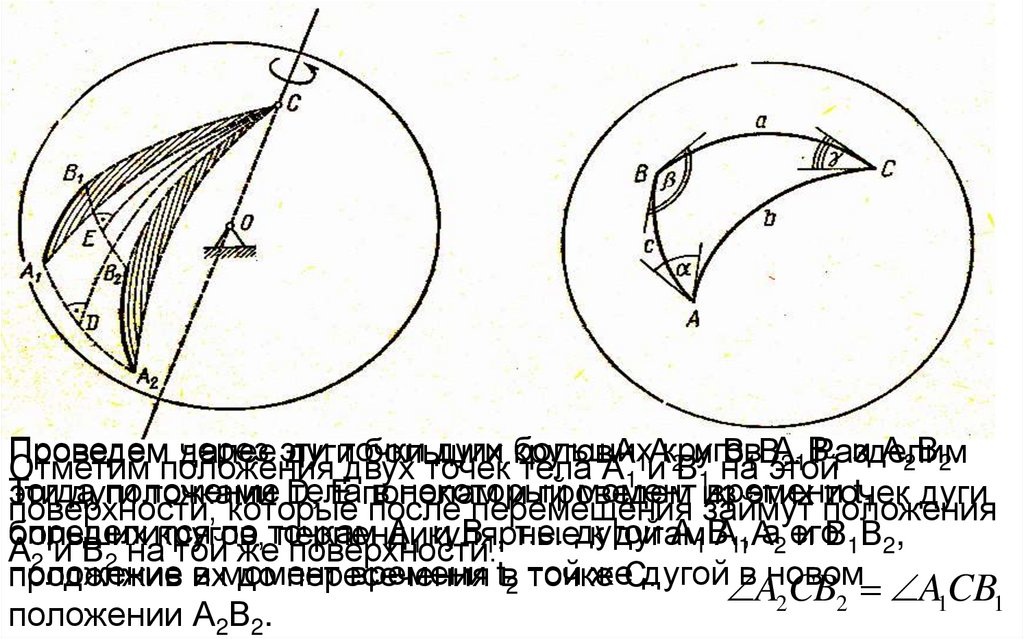
через
дуги больших1Акругов
А2.1В
Проведем
далее эти
дугиточки
больших
В1Вэтой
Разделим
1 и А2В2.
Отметим положения
двух
точек круговА
тела А1 и 2Ви1 на
Тогда
положение
тела
в некоторый
момент из
времени
t1 дуги
эти
дуги
точками
D,
E пополам
и проведем
этих положения
точек
поверхности,
которые
после перемещения
займут
определится
по точкам А1 и В1, т.е. дугой
А1ВА11,Аа2 его
больших
к дугам
и В1В2,
А2 и В2 накругов,
той жеперпендикулярные
поверхности.
положение их
в момент
времени tв2 точке
той жеС.дугой
вAновом
продолжив
до пересечения
2CB2 ACB
1
1
положении А2В2.

5.

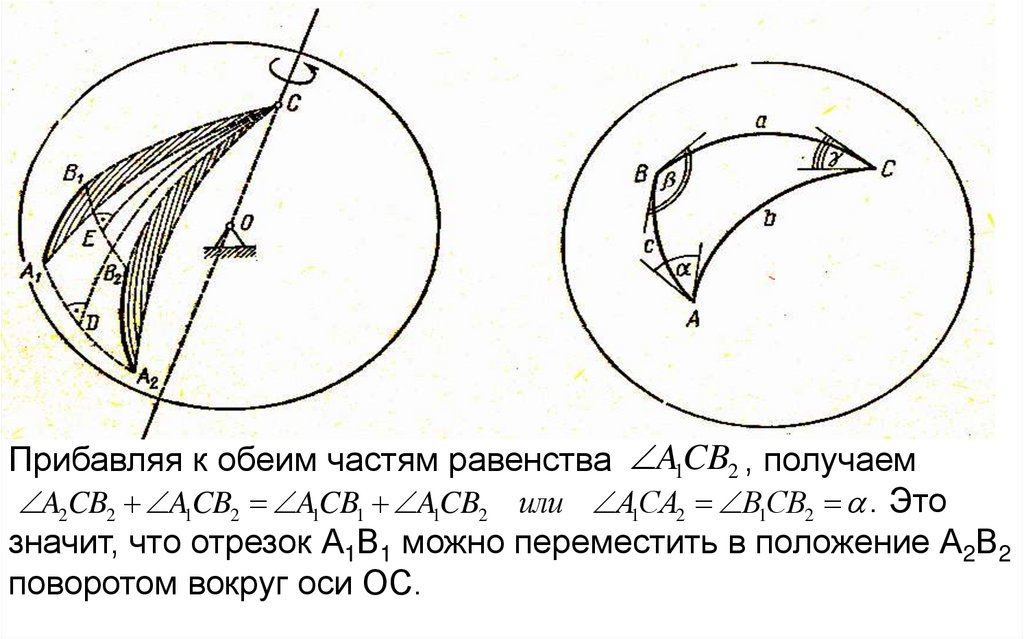
Прибавляя к обеим частям равенства ACB
1
2 , получаем
A2CB2 ACB
или ACA
1
2 ACB
1
1 ACB
1
2
1
2 B1CB2 . Это
значит, что отрезок А1В1 можно переместить в положение А2В2
поворотом вокруг оси ОС.

6.

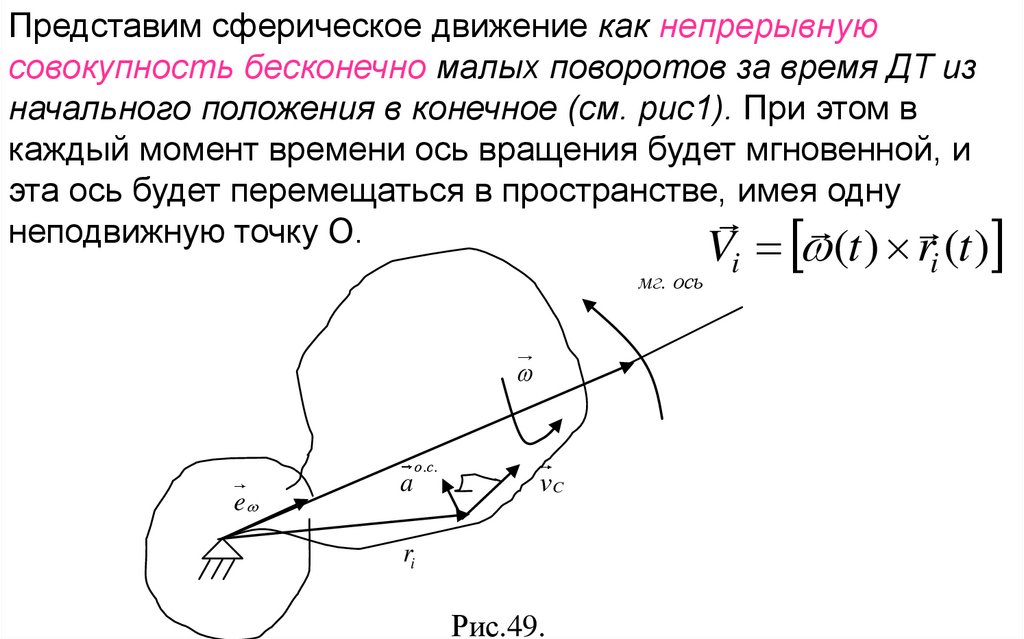
Представим сферическое движение как непрерывную
совокупность бесконечно малых поворотов за время ДТ из
начального положения в конечное (см. рис1). При этом в
каждый момент времени ось вращения будет мгновенной, и
эта ось будет перемещаться в пространстве, имея одну
неподвижную точку О.
мг. ось
e
a
о .с .
vC
ri
Рис.49.
Vi (t ) ri (t )

7.

По формуле Ривальса:
вр ос
a ai ai i (t ) ri (t ) (t ) Vi (t )
d
e
d d
( (t )e (t )) e
dt dt
dt
e (t ) 1 t
На основании теоремы о производной от единичного вектора
по параметру имеем:
Вывод для ε:
de
e
dt

8.

вращается вокруг некоторой переносной оси по поверхности сферы
единичного радиуса.
по определению:
d
dt
d d (t )e (t )
de
в e
dt
d d
( (t )e (t )) e в e
dt dt
e в

9.

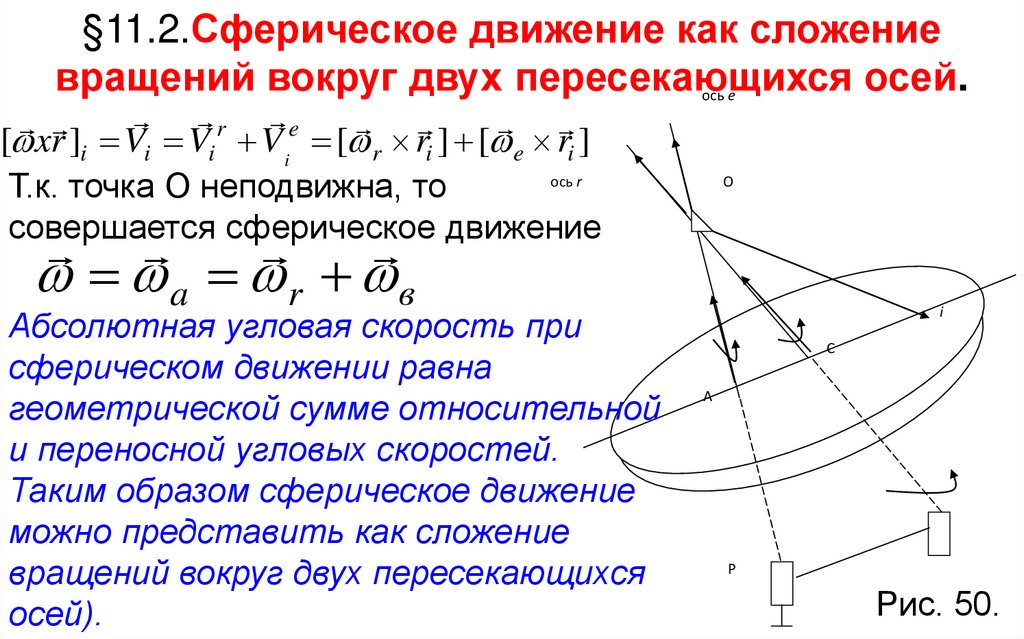
§11.2.Сферическое движение как сложение
вращений вокруг двух пересекающихся осей.
r e
[ xr ]i Vi Vi V i [ r ri ] [ e ri ]
ось r
Т.к. точка О неподвижна, то
совершается сферическое движение
ось e
О
a r в
Абсолютная угловая скорость при
сферическом движении равна
геометрической сумме относительной
и переносной угловых скоростей.
Таким образом сферическое движение
можно представить как сложение
вращений вокруг двух пересекающихся
осей).
i
С
А
Р
Рис. 50.

10.

§11.3. Общий случай. Сферическое движение как
сложение вращений вокруг трех пересекающихся осей.
Углы Эйлера.
Теорема о сложении скоростей для сферического
движения.
Сферическое движение нельзя представить как
совокупность трех поворотов вокруг осей x, y, z, т.к.
различная последовательность поворотов приводит к
разным конечным положениям тела. Действительно,
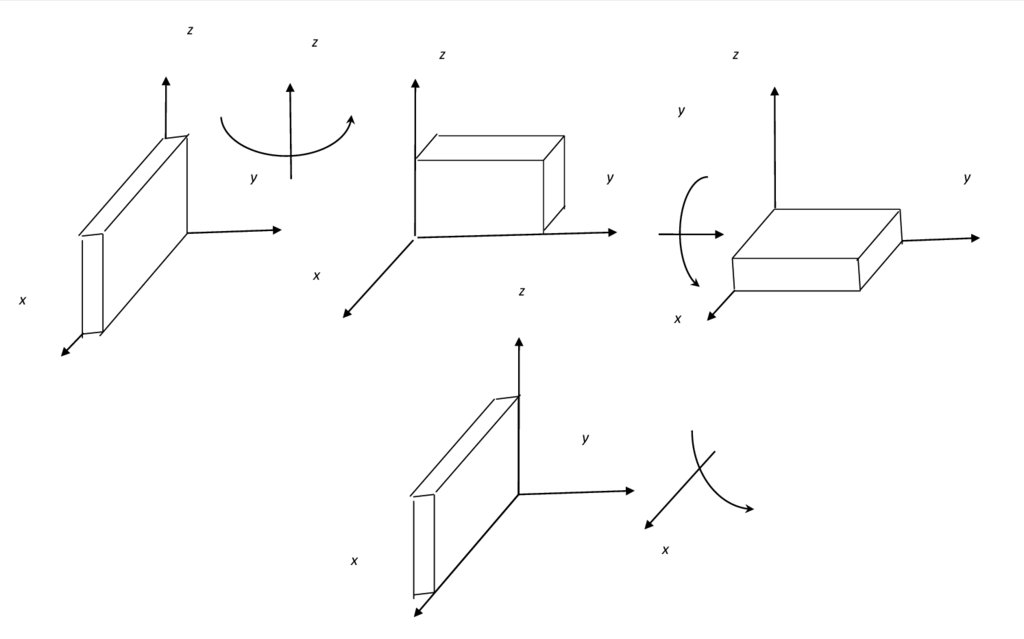
последовательность поворотов на π/2, представленная на
рисунке приводит к следующим положениям тела.

11.

z
z
z
z
y
у
у
у
х
z
х
х
у
х
х

12.

Другие последовательности поворотов вокруг осей приводят, к
другим конечным положениям, в чем убедимся
самостоятельно. Таким образом, мы видим, что
Повороты вокруг осей (x,y,z) не могут быть положены в
основу кинематики сферического движения твердого
тела, т.к. их различная последовательность приводит
тело в разные конечные положения. Это делает
теорию таких поворотов неоднозначной.
Леонард Эйлер был первым, кто придумал углы для которых
Разные последовательные повороты приводят к
однозначному конечному положению тела, т.е. могут
быть положены в основу кинематики сферического
движения.

13.

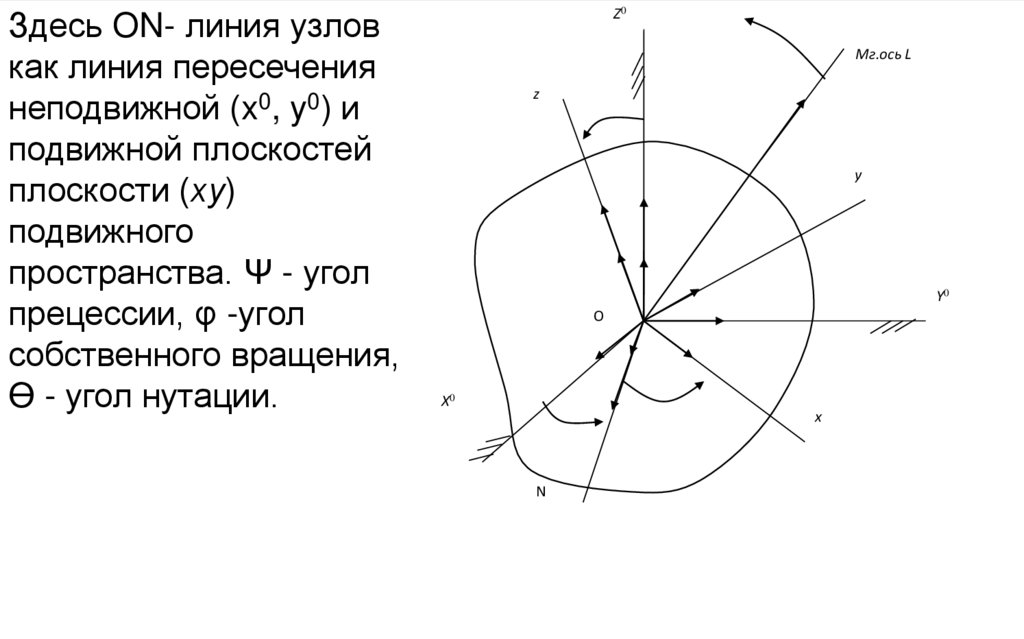
Здесь ON- линия узлов
как линия пересечения
неподвижной (x0, y0) и
подвижной плоскостей
плоскости (ху)
подвижного
пространства. Ψ - угол
прецессии, φ -угол
собственного вращения,
ϴ - угол нутации.
Z0
Мг.ось L
z
y
Y0
O
X0
x
N

14.

Уравнение мгновенной оси имеет вид V
rL 0
L
d
,
dt
0
d d d d d k d k d n
k0 k n ,
d
,
dt
r k ,
e k0 n.

15.

Т.о. сферическое движение имеет три степени свободы:
S 3 1 1 1
(t )
(t )
(t )
-3 кинематических уравнений Эйлера, задающих сферическое
движение, и определяющие законы сферического движения.
vi r i
ai r i vi
x y z k 0 k n

16.

В динамике будем делать все вычисления в подвижных осях(
вычисления в проекциях на эти оси)
z Прz k (k 0 k ) (kk ) (nk ) cos
x ( i) (k 0 i) (ki) (ni)
!k 0 k cos b sin k cos (i sin j cos )sin
cos ((ki) cos (ii)sin (i j ) cos )sin cos sin sin
y ( j ) (k 0 j ) (k j ) (n j )
!k 0 k cos b sin k cos (i sin j cos )sin
k j cos (i j sin j j cos )sin sin cos sin sin

17.

Проекция на неподвижные оси:
x sin sin cos
y sin cos sin
z cos