Движение тела вокруг неподвижной точки под действием силы тяжести. Случай Лагранжа

1. ДИНАМИКА ТВЕРДОГО ТЕЛА

ЛЕКЦИЯ 8:
ДВИЖЕНИЕ ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ
ТОЧКИ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ.
СЛУЧАЙ ЛАГРАНЖА

2. 1. Уравнения Пуассона

OXYZ
Oxyz
неподвижная система координат
подвижная система координат (ПСС),
жестко связанная с телом
G a, b, c
центр тяжести
n 1, 2 , 3 единичный вектор верт. оси OZ
в ПСС
Выражение компонент орта n через углы Эйлера
1 sin sin , 2 sin cos , 3 cos
dn
dn
0
ω n 0 Уравнения Пуассона
dt
dt
d 1
d 2
d 3
r 2 q 3 ,
p 3 r 1 ,
q 1 p 2
dt
dt
dt

3. 2. Динамические уравнения Эйлера при наличии силы тяжести

Ap C B qr M xe
Динамические уравнения
Bq A C rp M ye Эйлера в общем случае
Cr B A pq M ze
MO OG Pn
M x P 2c 3b
M y P 3a 1c
M z P 1b 2a
Ap C B qr P 2c 3b
Bq A C rp P 3a 1c
Cr B A pq P 1b 2a
Динамические уравнения Эйлера для
движения тяжелого твердого тела

4. 3. Уравнения движения тяжелого твердого тела вокруг неподвижной точки

1 r 2 q 3
2 p 3 r 1
Замкнутая система уравнений для
нахождения
3 q 1 p 2
Ap C B qr P 2c 3b
1 (t ), 2 (t ), 3 (t ), p(t ), q(t ), r(t )
Bq A C rp P 3a 1c
Cr B A pq P 1b 2a
После нахождения
1 (t ), 2 (t ), 3 (t ), p(t ), q(t ), r(t )
зависимости
(t ), (t )
находятся из условий
1 sin sin , 2 sin cos , 3 cos
а оставшийся угол Эйлера
(t ) из одного из кинематических уравнений Эйлера
p sin sin cos
q sin cos sin
r cos

5. 4. Первые интегралы системы

1)
12 22 32 1
n 1
2) Теорема об изменении кинетического момента
Реакция опоры и сила тяжести не создают момента относительно оси OZ
K O n const
Ap 1 Bq 2 Cr 3 const
3) Сохранение энергии
T const
1
T Ap 2 Bq 2 Cr 2
2
Ph P OG n P a 1 b 2 c 3
Ap
2
Bq 2 Cr 2 2 P a 1 b 2 c 3 const
Из общей теории множителя Якоби известно, что для того,
чтобы интегрирование исходной системы можно было
свести к квадратурам при любых начальных условиях,
нужно найти еще один независимый от них интеграл.

6. 5. Известные случаи интегрируемости

А) Случай Эйлера: тело произвольно, но его центр тяжести находится в
неподвижной точке О
a b c 0
дополнительный интеграл KO2 A2 p 2 B 2 q 2 C 2 r 2 const
В) Случай Лагранжа: эллипсоид инерции тела для неподвижной точки является
эллипсоидом вращения, а центр тяжести находится на оси вращения
A B, a b 0
r const
дополнительный интеграл
С) Случай Ковалевской: эллипсоид инерции для точки О является эллипсоидом
вращения вокруг оси Oz, момент инерции относительно этой оси вдвое меньше двух
других, а центр тяжести тела лежит в экваториальной плоскости эллипсоида инерции
A B 2C , c 0
дополнительный интеграл
p 2 q2 1 2 pq 2 const
2
2
=
Pa
C

7. 6. Вывод уравнения для угла нутации в случае Лагранжа

12 22 32 1
(2) A p 1 q 2 Cr 3 b
2
2
(3) A p q 2 Pc 3 2e
(1)
1 r 2 q 3
2 p 3 r 1
q
p
A
(4)
3 q 1 p 2
Ap C A rq P 2c 2
Aq C A rp P 1c 1
q 1 p 2 r q 2 p 1 3 p 2 q 2
A q 1 p 2 C A r q 2 p 1 Pc 12 22
d
q 1 p 2 Cr q 2 p 1 A 3 p 2 q 2 Pc 12 22
dt
2
b Cr 3
2
(
e
Pc
)
Pc
1
3
3
A
(1)
3
(4)
(2) Cr
3
A
(3)
d
2 d
2
2 3 A2 3 2 3
A2 32 3 3
A
3 3 3
dt
dt
A

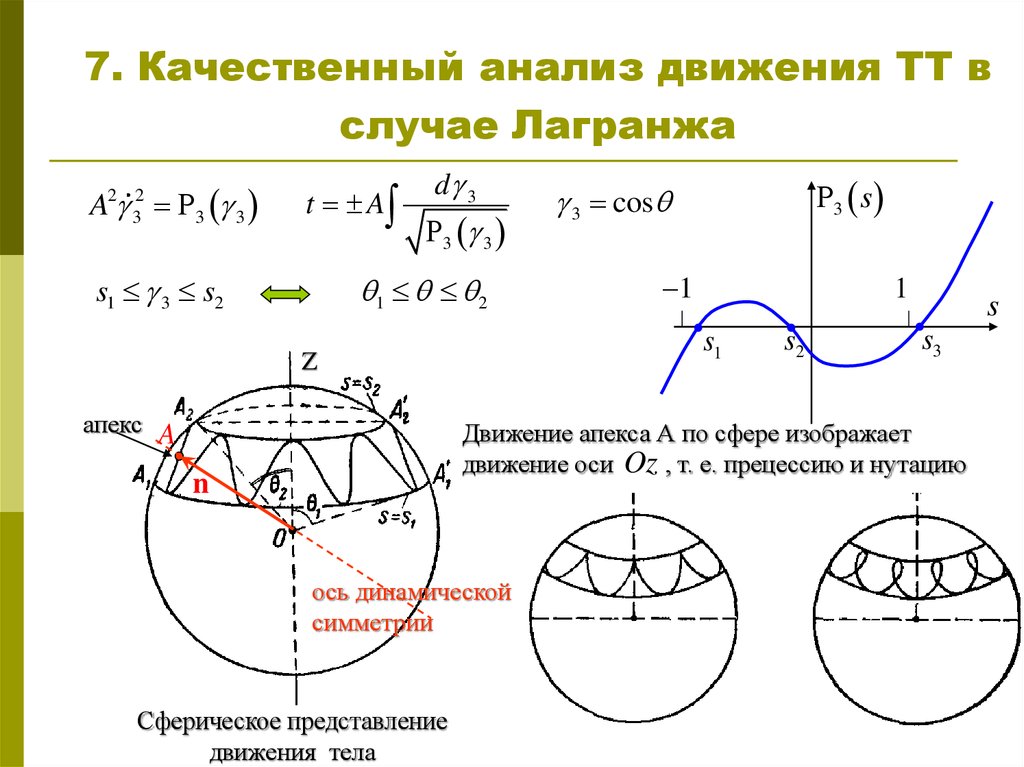
8. 7. Качественный анализ движения ТТ в случае Лагранжа

A2 32 3 3
t A
s1 3 s2
d 3
3 3
1 2
1
1
s1
Z
апекс A
3 s
3 cos
s2
s
s3
Движение апекса А по сфере изображает
движение оси Oz , т. е. прецессию и нутацию
n
ось динамической
симметрии
Сферическое представление
движения тела

9. 8. Быстро вращающееся тело: псевдорегулярная прецессия

Начальные условия
размерности
t 0 : , 0, 0 , 0
f , C, c, P, A / C, 0
ML
1
2
ML
L
1
1
1
T2
T
Аргументами должны являться безразмерные комплексы,
а не размерные параметры, иначе ответ будет зависеть от
единиц измерения
cP
f 2 , A / C , 0
C
Быстро вращающееся тело – большие
– малые значения параметра
cP
2C
0 c 0 случай Эйлера вращения симметричного тела
0 0 (регулярная прецессия) f , A / C, 0 0 0
A
2
Раскладывая в ряд Тейлора f , A / C , 0 b( A / C , 0 ) O
b sin 0
C
Когда велика, изменение угла нутации настолько мало, что
прецессия кажется регулярной. Такая нерегулярная прецессия, мало
отличающаяся от регулярной, называется псевдорегулярной прецессией.
точный
результат

10. 9. О пользе анализа размерностей

Доказательство теоремы Пифагора
Треугольник, а, значит, и его площадь,
полностью определяется величинами c и
размерности
c
S
S
f ( c, )
2
c
L 1
1
S c f ( )
2
S S1 S2
c2 f ( ) b2 f ( ) a 2 f ( )
c 2 b2 a 2
S2
a
c
S1
b