Основные задачи динамики твердых тел. Уравнения Эйлера. Вращение вокруг неподвижной оси

1. ДИНАМИКА ТВЕРДОГО ТЕЛА

ЛЕКЦИИ 3-4:
ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ ТТ.
УРАВНЕНИЯ ЭЙЛЕРА.
ВРАЩЕНИЕ ВОКРУГ НЕПОДВИЖНОЙ ОСИ

2. 1. Основные задачи динамики твердого тела

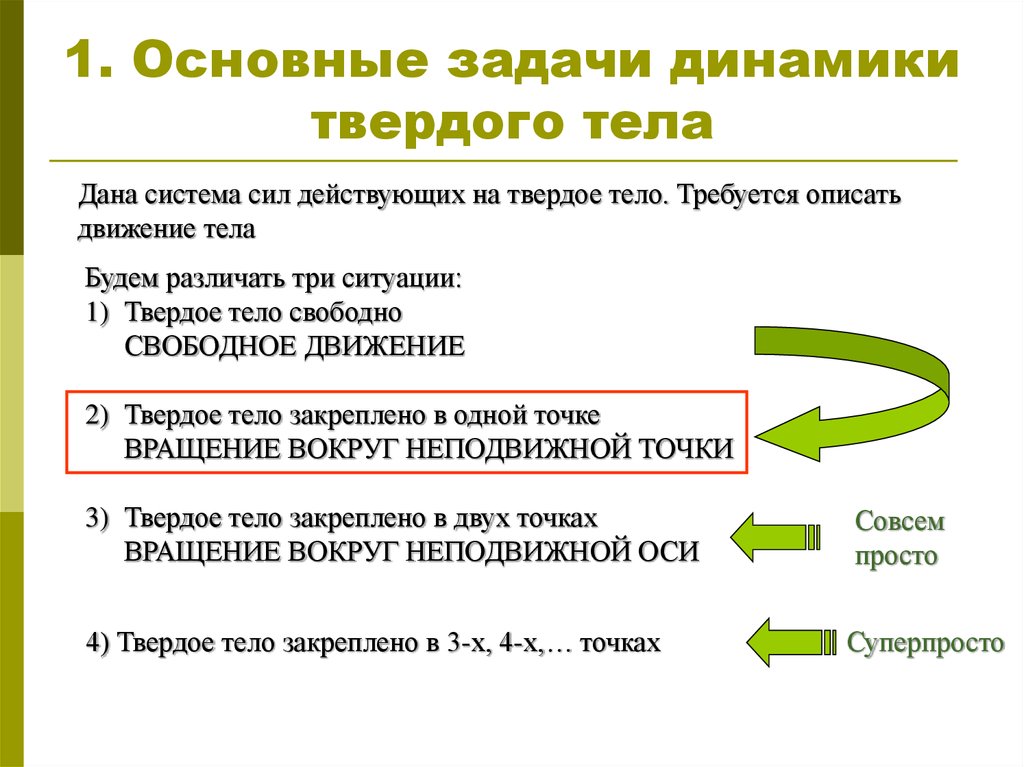
Дана система сил действующих на твердое тело. Требуется описать
движение тела
Будем различать три ситуации:
1) Твердое тело свободно
СВОБОДНОЕ ДВИЖЕНИЕ
2) Твердое тело закреплено в одной точке
ВРАЩЕНИЕ ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
3) Твердое тело закреплено в двух точках
ВРАЩЕНИЕ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Совсем
просто
4) Твердое тело закреплено в 3-х, 4-х,… точках
Суперпросто

3. 2. Исходные ур-ия движение свободного твердого тела

Свободное твердое тело имеет шесть степеней свободы
Например: координаты центра масс и углы Эйлера, определяющие
ориентацию тела относительно центра масс
Для описания движения нужны шесть уравнений.
Первые три из них даются теоремой о движении центра масс
dvC
M
F
dt
d 2rC
M 2 F
dt
rC (t )
Они служат для нахождения положения центра масс
Вторые три – теоремой об изменении момента количеств движения
dK O
MO
dt
Эти уравнения будут служить для нахождения ориентации тела
относительно центра масс

4. 3. Сведение к задаче о враще-нии вокруг неподвижной точки

3. Сведение к задаче о вращении вокруг неподвижной точки
Z
dK O
MO
dt
MO ρk Fk rk rC Fk
k
C
x rC
k
rk Fk rC Fk MC rC F
k
z
k
O
rk
ρk
y
mk
Y
X
K O mk ρk ρk mk rk rC rk rC
k
k
d
mk rk rk rC mk rk mk rk rC rC rC mk
k
dt k
k
k
dK O dK C
dK C
M rC rC rC rC
rC F
dt
dt
dt
dK C
MC
dt
Теорема об изменении момента количеств движения
дает те же уравнения как будто бы твердое тело
вращалось вокруг неподвижной точки C

5. 4. Вычисление момента количеств движения

ω
K O mk rk v k mk rk ω rk
k
k
i
j
ω rk X
Y
Xk
Yk
rk ω rk
Z
i Z k Y Yk Z
k
Z j X k Z Z k X
Zk
k Yk X X k Y
i
j
k
Xk
Yk
Zk
Z k Y
X k Z
Yk X
Yk Z
Z k X
X k Y
C O
x X
y Y
z Z
O
rk
X
Y
mk
j X Z Y X Z Y
k X Y Z X Z Y
i X Yk2 Z k2 Y Yk X k Z Z k X k
2
k
Y
Z
2
k
2
k
2
k
X
k
X
k
k
Z
k
k k
Y
k k
KO i I X X I XY Y I XZ Z j IY Y I XY X IYZ Z k I Z Z I XZ X IYZ Y

6. 5. Уравнения вращения в непод-вижной системе координат

5. Уравнения вращения в неподвижной системе координат
dK O
MO
dt
d
I X X I XY Y I XZ Z M OX
dt
d
IY Y I XY X IYZ Z M OY
dt
d
I Z Z I XZ X IYZ Y M OZ
dt
Z
z
y
O
Y
x
X
НЕУДОБНЫ. Потому что не только компоненты ω, но и тензора
инерции изменяются со временем из-за того, что тело со временем
изменяет свою ориентацию относительно неподвижных осей.
ИДЕЯ№1: Перейти в подвижную систему координат, жестко
связанную с телом XYZ xyz
ИДЕЯ№2: Направить оси (xyz) по главным осям тензора инерции для
точки О

7. 6. Воспоминания из кинематики

dK O
MO
dt
MOX , MOX , MOX MO MO MOx , MOz , MOz
z
KOX , KOX , KOX KO KO KOx , KOz , KOz
x
KOX , KOY , KOZ
x
y
y
z
z
dK O dK O
KOx , KOy , KOz
dt
dt
y
O
=
I , I , I
Z
Y
x
X
dK O d
K0 x i K0 y j K0 z k K0 x i K0 y j K0 z k K0 x i K0 y j K0 z k
dt
dt
dK O
dt
di
ω i,
dt
dj
ω j,
dt
dk
ω k,
dt
dK O dK O
ω KO
dt
dt

8. 7. Уравнения Эйлера

dK O
ω K O MO
dt
i
ω K O x
I x x
j
y
I y y
k
i I z I y y z
z j I x I z x z
I z z k I y I x x y
Полная система уравнений вращения тела вокруг неподвижной точки
x sin sin cos
+
y sin cos sin
z cos
ПОВТОРИТЬ!
d x
Ix
I z I y y z M Ox
dt
d y
Iy
I x I z x z M Oy
dt
d z
Iz
I y I x x y M Oz
dt
Динамические уравнения Эйлера Кинематические уравнения Эйлера

9. 8. Вращение вокруг неподвижной оси

Рассмотрим твердое тело, имеющее 2 неподвижные точки О, О1
OXYZ
Oxyz
F, F1
R, MO
неподвижная система координат
подвижная система координат, жестко связанная с телом
реакции связей в О, О1
главный вектор и главный момент внешних сил
1) теоремы об изменении количества движения и момента
количества движения (в неподвижной системе координат)
M
dv C
R F F1
dt
dK O
MO OO1 F1
dt
2) переход в подвижную систему координат
dvC
M
Mω vC R F F1
dt
(1)
dK O
ω K O MO OO1 F1 (2)
dt
воспользовались известным из
кинематики фактом:
абсолютная
производная
da da
ω a
dt dt
относительная
производная

10. 9. Теорема об изменении количества движения

3) вычисляем фигурирующие в (1) вектора в подвижной СК
dvC
Mω vC R F F1
dt
F1 x
Rx
0
F1 F1 y
R R y
ω 0
F
R
1z
z
M
Fx
F Fy
F
z
i
j
v C ω OC 0
0
xC
yC
ω vC
i
j
0
0
yC xC
yC
xC
zC 0
k
2 xC
2 yC
0 0
k
MyC MxC 2 Rx Fx F1 x
MxC MyC 2 Ry Fy F1 y
0 Rz Fz F1z

11. 10. Теорема об изменении момента количеств движения

4) вычисляем фигурирующие в (2) вектора в подвижной СК
dK O
ω K O MO OO1 F1
dt
Mx
i
j
k hF1 y
M O M y
OO1 F1 0
0
h hF1 x
M
F1 x F1 y F1z 0
z
xz
i
j k
K O r × ω × r dxdydz x
y z dxdydz yz dxdydz
2
2
y x 0
x
y
i
j
k
I xz
2
I yz
I
I
M x hF1 y
xz
yz
2
I yz ω × K O 0
0
I xz
2
I
I
M y hF1x
I
yz
xz
I xz I yz I z 0
z
I z M z

12. 11. Уравнения движения

I z M z
диф. ур-ие вращения Т.Т вокруг оси
MyC MxC 2 Rx Fx F1 x
MxC MyC 2 Ry Fy F1 y
I xz I yz 2 M x hF1 y
уравнения для определения
поперечных реакций
I yz I xz 2 M y hF1x
0 Rz Fz F1z
уравнение для определения
Fz F1z

13. 12. Пример

Равнобедренный прямоугольный треугольник вращается вокруг
вертикальной оси, к которой он подвешен своим катетом. Найти
боковые давления на опоры. Треугольник считать тонкой
однородной пластинкой.
a
h a
3
a
z
2M
Ma 2
I yz yzdm 2 z ydy dz
a 0 0
4
Mga
Rx R y M z M y 0, Rz Mg , M x
3
xC 0
yC
1
1
Ma F1 x Fx , Ma 2 F1 y Fy , Mg Fz F1z
3
3
1
1
1
Ma 2 2 Mga aF1 y , Ma 2 aF1 x , I z 0
4
3
4
M
a 2 4 g
12
M
F1 y
3g 5a 2
12
F1x Fx 0
Fy

14. 13. Условия совпадения динами-ческих и статических реакций

13. Условия совпадения динамических и статических реакций
MxC MyC 2 Ry Fy F1 y
MyC MxC 2 Rx Fx F1 x
I yz I xz 2 M y hF1x
I xz I yz 2 M x hF1 y
Ry Fy F1 y 0, Rx Fx F1x 0
M y hF1 x 0, M x hF1 y 0
уравнения для определения
динамических поперечных
реакций
уравнения для определения
статических поперечных реакций
При каких условиях динамические поперечные реакции совпадают со статическими?
MxC MyC 2 0
MyC MxC 2 0
I yz I xz 2 0
I xz I yz 2 0
ур-ия для
xC , yC
ур-ия для
I xz , I yz
определитель
обеих систем
xC yC I xz I yz 0
2 4 0
Динамические реакции при вращении твердого тела равны статическим
Ось вращения является главной центральной осью инерции тела.

15. 14. Альтернативная форма ур-й для определения поперечных реакций

2
(1) MxC MyC Ry Fy F1 y Исходные уравнения для
Axyz
2
определения
динамических
My
Mx
R
F
F
(2)
C
C
x
x
1x
z
2
поперечных
реакций
(3) I yz I xz M y hF1x
(4) I xz I yz 2 M x hF1 y
z B B
O
2
(1a)
Mx
My
R
F
F
C
C
y
Ay
By
xC xC , yC yC
2
MyC MxC Rx FAx FBx (2a) x
z A
A
I yz I y z z A yC M
hF1x z B z A FBx
x
M y zk Fkx xk Fky zk z A Fkx xk Fky M y z A Rx
k
y
y
k
I xz xzdm x z z A dm I x z z A x xC xC dm I x z z A xC M
(3)
I y z I x z 2 M y z A Rx z B z A FBx z A MyC MxC 2 (2a)
M y z A FAx FBx z B z A FBx M y z AFAx z B FBx

16. 15. Альтернативная форма ур-й для определения поперечных реакций

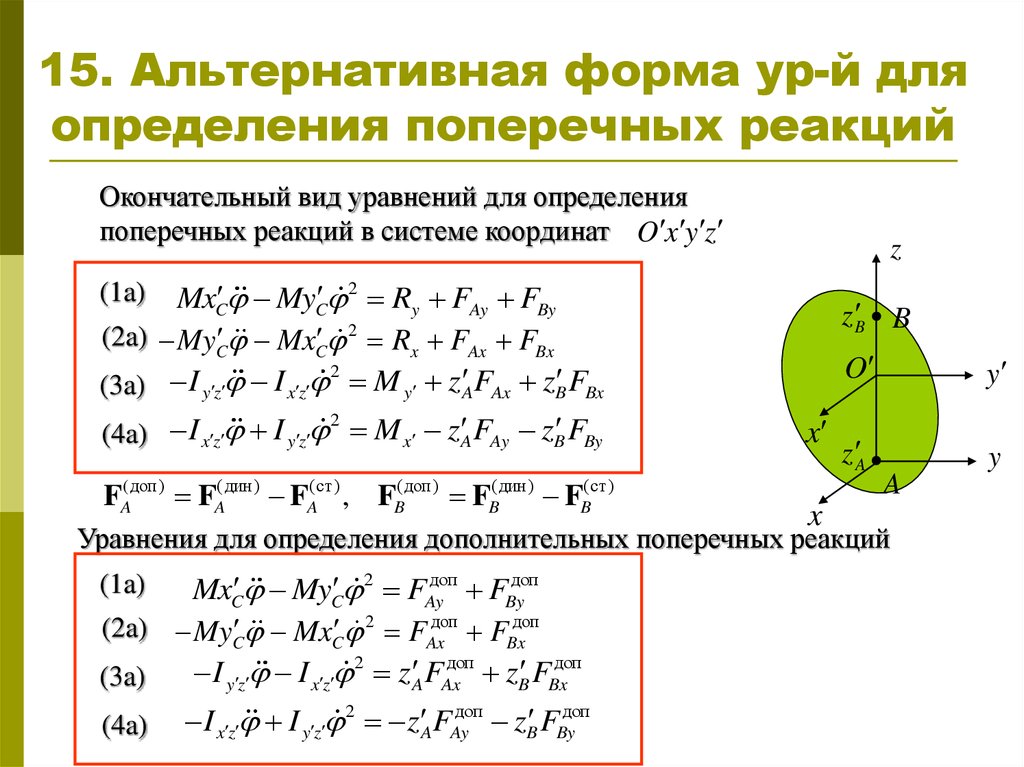
Окончательный вид уравнений для определения
поперечных реакций в системе координат O x y z
z
MxC MyC 2 Ry FAy FBy
(2a) MyC MxC 2 Rx FAx FBx
2
(3a) I y z I x z M y z AFAx zB FBx
(1a)
2
(4a) I x z I y z M x z AFAy zB FBy
z B B
x
O
y
z A
y
A
FA( доп) FA( дин) FA(ст ) , FB( доп) FB( дин) FB(ст )
x
Уравнения для определения дополнительных поперечных реакций
(1a)
MxC MyC 2 FAyдоп FByдоп
(2a) MyC MxC 2 FAxдоп FBxдоп
I y z I x z 2 z AFAxдоп zB FBxдоп
(3a)
(4a)
I x z I y z 2 z AFAyдоп zB FByдоп

17. 16. Пример 1

Центр тяжести махового колеса, вес которого Р = 300 кГ, находится на
расстоянии 1 мм от горизонтальной оси вала; расстояния подшипников
от колеса равны между собой. Найти реакции подшипников, если вал
вращается равномерно, делая n=1200 об/мин. Маховик имеет
плоскость симметрии, перпендикулярную к оси вращения.
A
y
x1
z
C
O
2 n
40 c 1
xC 1мм, yC I xz I yz 0 0,
l
l
60
(ст)
(ст)
(ст)
Статические реакции
FAy(ст)
F
0
F
F
By1
Ax1
Bx1 P / 2 150 кГ
1
Дополнительные реакции
MxC 2 FAx(доп) FBx(доп)
0 F
(доп)
Ay
F
(доп)
By
0 lFAy(доп) lFBy(доп)
0 lFAx(доп) lFBx(доп)
FA( доп) FA( дин) FA(ст ) , FB( доп) FB( дин) FB(ст )
FAy(доп) FBy(доп) 0
FAx(доп) FBx(доп)
x
M
xC 2 240 кГ
2
B

18. 17. Пример 2: постановка задачи

Вычислить добавочные динамические
x
x2 BO b
AO
a
реакции в подшипниках А и В при
вращении вокруг оси АВ однородного
тонкого кругового диска CD, предполагая,
z
B
что ось АВ проходит через центр диска, A
O
но вследствие неправильного рассверz2
y
y
2
ливания втулка составляет с перпендикуляром к плоскости диска AOE 0.02 рад
Дано: масса диска m = 3,27 кГ, радиус его r = 20 см, число оборотов
n = 30 000 об/мин, расстояния AO = 50 см, ОВ = 30 см.
xC yC 0, z A a 50 см, zB b 30 см
Статические реакции
FAy FBy 0
b
3
mg 12.05 Н
a b 8
a
5
FBx mg
mg 20 Н
a b 8
FAx mg

19. 18. Пример 2: вычисление моментов инерции. Способ 1.

x2
x
x2 x cos z sin
y2 y
z2 x sin z cos
x
z
A
x2
z
O
z2
F ( x2 , y2 , z2 ) I x2 x22 I y2 y22 I z2 z22 2I x2 y2 x2 y2 2I y2 z2 y2 z2 2I z2 x2 z2 x2
y y2
B
z2
1
1
mr 2 z22 mr 2 x22 y22
2
4
1 2 2 2
1
mr x sin z 2 cos2 xz sin 2 mr 2 y 2 x 2 cos2 z 2 sin 2 xz sin 2
2
4
1
1 2
mr 2
2
2 1
2
2
2 1
2
2
2 1
2
x mr sin cos y mr z mr cos sin xz
sin 2
4
4
4
4
2
2
Ix
Iy
Iz
2 I xz

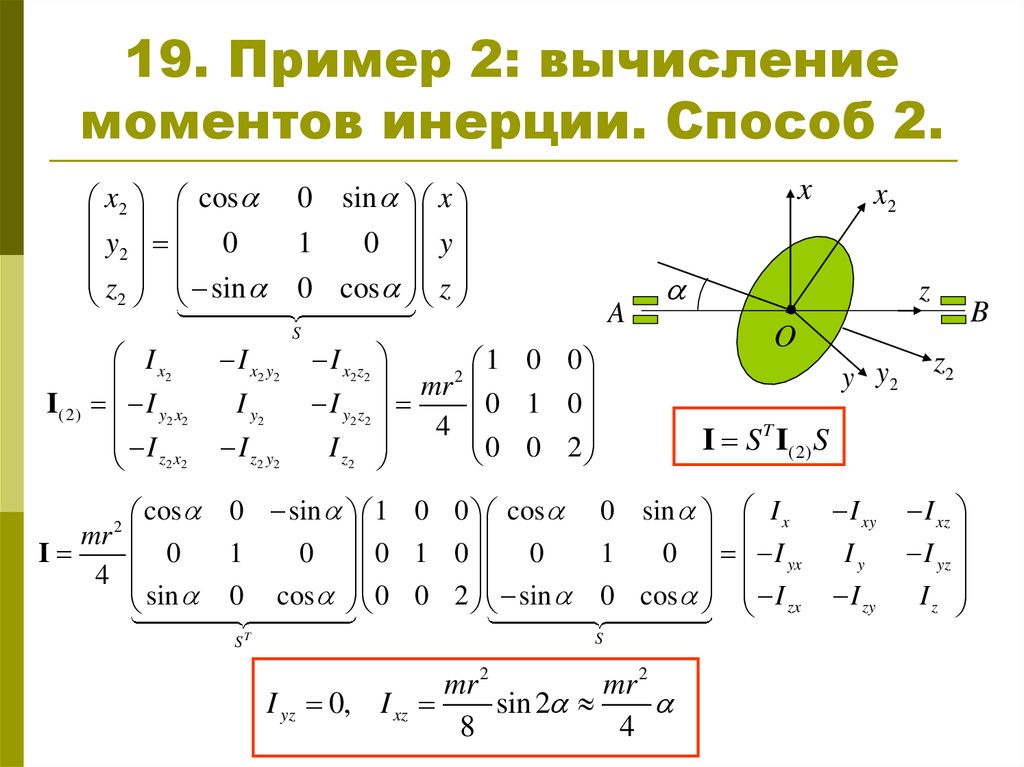
20. 19. Пример 2: вычисление моментов инерции. Способ 2.

x2 cos
y 0
2
z sin
2
I(2)
I x2
I y2 x2
Iz x
22
cos
mr
I
0
4
sin
2
I x2 y2
I y2
I z2 y 2
0 sin x
1
0 y
0 cos z
S
A
x2
I x2 z2
1 0 0
2
mr
I y 2 z2
0
1
0
4
I z2
0 0 2
0 sin 1 0 0 cos
1
0 0 1 0 0
0 cos 0 0 2 sin
ST
x
z
O
y y2
B
z2
I S T I(2) S
0 sin I x
1
0 I yx
0 cos I zx
S
mr 2
mr 2
I yz 0, I xz
sin 2
8
4
I xy
Iy
I zy
I xz
I yz
I z

21. 20. Пример 2: завершение

MxC MyC F
доп
Ay
2
x
F
доп
By
MyC MxC 2 FAxдоп FBxдоп
I xz I yz 2 z A FAyдоп z B FByдоп
a
A
z
O
b
y y2
I yz I xz 2 z A FAxдоп zB FBxдоп
a
доп
Ay
F
F
доп
By
0
2 n
1000 рад/с.
60
x2
b
FAxдоп FBxдоп
I xy 2
mr 2 2
a b 4 a b
FAxдоп FBxдоп 8000 Н
B
z2

22. 21. Физический маятник

Физическим маятником называется твердое тело, вращающееся
вокруг неподвижной оси под действием силы тяжести.
Рассмотрим случай, когда ось вращения горизонтальна.
Проведем через центр тяжести С тела плоскость,
перпендикулярную к оси вращения. Точка пересечения О
этой плоскости с осью вращения называется точкой
подвеса.
диф. ур-ие вращения тела вокруг оси z I z M z
M z Mga sin
уравнение движения
физического маятника
Случай малых колебаний
Mga
sin 0
Iz
sin
Период колебаний
k 2 0, k 2
T
Mga
Iz
2
Iz
2
k
Mga

23. 22. Теорема Гюйгенса

уравнение движения
физического маятника
Mga
sin 0
Iz
уравнение движения
математического маятника
g
sin 0
l
Iz
Математический маятник с длиной
l
будет двигаться как физический
Ma
Iz
I C Ma 2
IC
l
a
Ma
Ma
Ma
a1
Приведенная длина
физического маятника
Центр
качания
Свойство взаимности (теорема Гюйгенса): Если старый центр качания сделать новой
точкой подвеса, то старая точка подвеса станет новым центром качания
Д-во:
l ( new )
IC
a1 a a1 l
Ma1

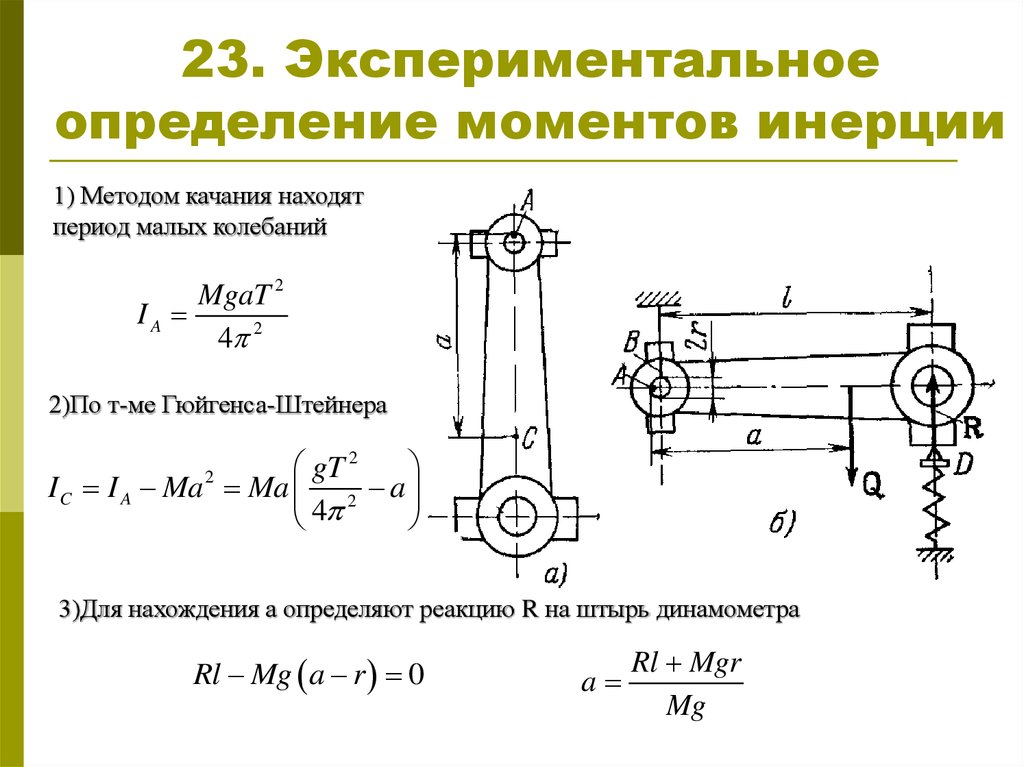
24. 23. Экспериментальное определение моментов инерции

1) Методом качания находят
период малых колебаний
MgaT 2
IA
4 2
2)По т-ме Гюйгенса-Штейнера
gT 2
I C I A Ma Ma 2 a
4
2
3)Для нахождения а определяют реакцию R на штырь динамометра
Rl Mg a r 0
a
Rl Mgr
Mg