Similar presentations:
Уравнение вращения твердого тела вокруг неподвижной оси. Момент инерции
1. ЛЕКЦИЯ 5.1 ДИНАМИКА ТВЕРДОГО ТЕЛА
Уравнение вращения твердого телавокруг неподвижной оси. Момент
инерции
1
2. Уравнения движения твердого тела
Для описания твердого тела (как системы частиц) имеютсядва уравнения – уравнение движения центра масс и
уравнение моментов:
dv C
m
Fвнеш ;
dt
i
dL
M внеш .
dt
i
Здесь vС – скорость центра масс, L – момент импульса
системы, Fвнеш – равнодействующая всех внешних сил, Mвнеш
– момент равнодействующей всех внешних сил (или сумма
моментов всех внешних сил).
2
3. Связь момента импульса твердого тела с угловой скоростью вращения
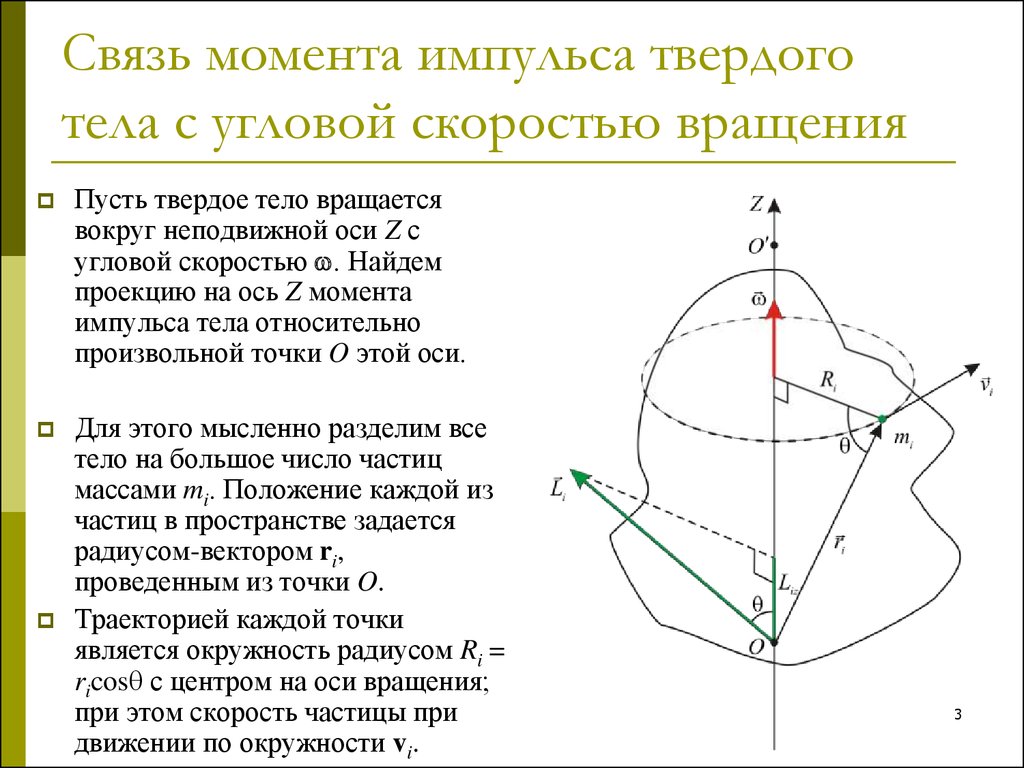
Пусть твердое тело вращаетсявокруг неподвижной оси Z с
угловой скоростью . Найдем
проекцию на ось Z момента
импульса тела относительно
произвольной точки O этой оси.
Для этого мысленно разделим все
тело на большое число частиц
массами mi. Положение каждой из
частиц в пространстве задается
радиусом-вектором ri,
проведенным из точки O.
Траекторией каждой точки
является окружность радиусом Ri =
ricos с центром на оси вращения;
при этом скорость частицы при
движении по окружности vi.
3
4. Связь момента импульса твердого тела с угловой скоростью вращения
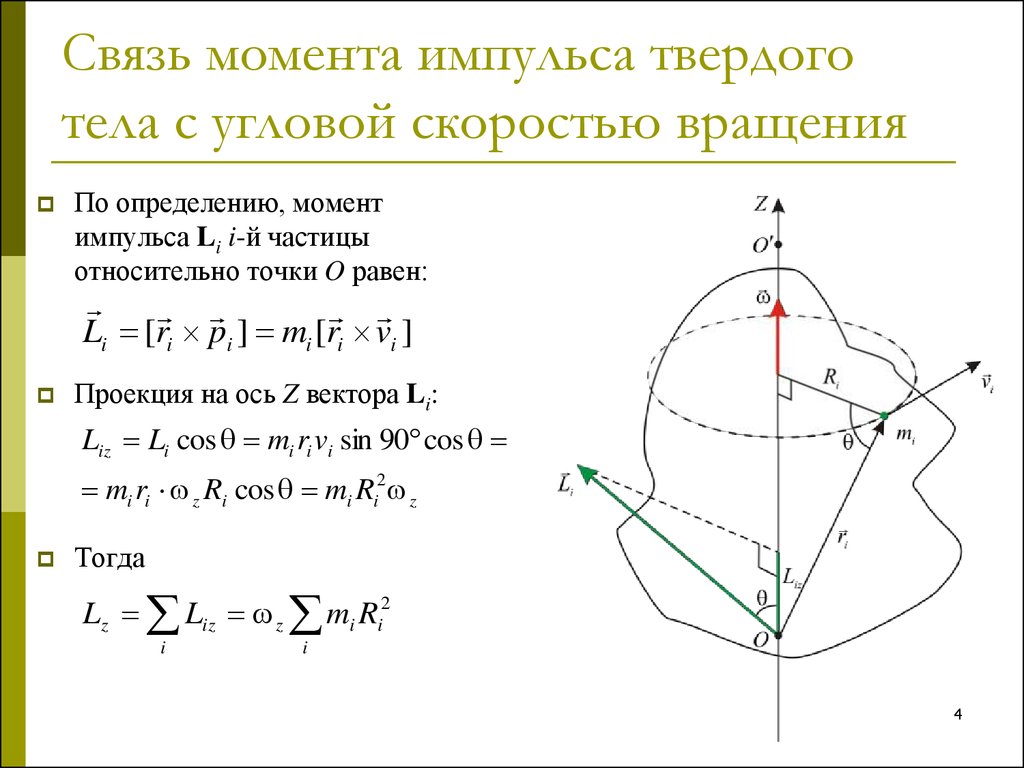
По определению, моментимпульса Li i-й частицы
относительно точки O равен:
Li [ri pi ] mi [ri vi ]
Проекция на ось Z вектора Li:
Liz Li cos mi ri vi sin 90 cos
mi ri z Ri cos mi Ri2 z
Тогда
Lz Liz z mi Ri2
i
i
4
5. Момент инерции твердого тела
Моментом инерции твердого тела относительно оси Zназывается величина:
I mi Ri2
i
Здесь mi – масса i-й частицы тела; Ri – расстояние от этой
частицы до оси Z.
Поскольку любое реальное твердое тело плотности и
объемом V есть совокупность бесконечно большого числа
частиц, то
I lim
N
N
2
2
2
m
R
R
dm
R
i i
dV
i 1
V
V
5
6. Физический смысл и свойства момента инерции
Момент инерции I характеризует распределениемассы тела по его объему.
Эта величина представляет собой количественную
меру инертности твердого тела по отношению к
любым попыткам изменить угловую скорость
твердого тела.
Момент инерции – величина аддитивная: момент
инерции тела относительно некоторой оси равен
сумме моментов инерции его частей, рассчитанных
относительно той же оси.
6
7. Моменты инерции некоторых симметричных твердых тел
Форма телаМатериальная точка
массой m
Положение
оси вращения
Проходит на
расстоянии r от точки
Момент
инерции I
mR2
Проходит через середину
стержня перпендикулярно его оси
(1/12)ml2
Проходит через один из концов
стержня перпендикулярно его оси
(1/3)ml2
Однородный диск
(сплошной цилиндр)
радиусом R и массой m
Проходит перпендикулярно
плоскости диска (совпадает с осью
цилиндра)
(1/2)mR2
Однородный диск
радиусом R и массой m
Проходит вдоль диаметра диска
(1/4)mR2
Однородный тонкостенный
полый цилиндр (труба, обруч)
радиусом R и массой m
Совпадает с осью цилиндра
(проходит перпендикулярно
плоскости обруча)
mR2
Однородный шар
радиусом R и массой m
Проходит через центр шара
(2/5)mR2
Тонкая прямоугольная
пластина массой m
со сторонами a и b
Проходит
перпендикулярно пластине через
точку пересечения диагоналей
Однородный
тонкий стержень
длиной l и массой m
(1/12)m(a2 + b2)
7
8. Связь между угловой скоростью вращения твердого тела и моментом импульса
Таким образом, с учетом определения моментаинерции, проекция на ось Z момента импульса
тела равна:
Lz I z
Проекция момента импульса тела Lz на ось Z не
зависит от положения точки O на этой оси
(поскольку I и z также не зависят от положения
точки O).
8
9. Связь между угловой скоростью вращения твердого тела и моментом импульса
Если твердое тело вращается вокруг оси Z,являющейся осью симметрии этого тела, или осью,
перпендикулярной оси симметрии, последнее
выражение можно записать в векторном виде:
L I
В остальных случаях L I .
9
10. Уравнение вращения твердого тела вокруг неподвижной оси
Пусть твердое тело вращается с угловой скоростью вокругнеподвижной оси Z. Обозначим через L момент импульса
тела относительно произвольной точки O оси Z, а через M –
сумму моментов всех приложенных к нему внешних сил.
Для твердого тела как системы материальных точек
справедливо уравнение моментов:
dL
M
dt
Перепишем его в проекции на ось Z:
dLz
Mz
dt
10
11. Уравнение вращения твердого тела вокруг неподвижной оси
Поскольку, как было показано выше, проекция на ось Zмомента импульса тела равна Lz = I z, то подставляя это
выражение в уравнение моментов, получим уравнение
вращения твердого тела вокруг неподвижной оси:
d z
I
M z I z M z
dt
Здесь I – момент инерции твердого тела относительно оси Z,
z = d z/dt – проекция на ось Z вектора углового ускорения
тела, Mz – проекция на ось Z момента всех внешних сил.
11
12. Пример использования уравнения вращения твердого тела вокруг неподвижной оси
Пример. Однородный цилиндр массы mи радиуса R может вращаться с трением
вокруг неподвижной оси Z,
совпадающей с его осью симметрии. На
цилиндр намотана тонкая нерастяжимая
невесомая нить, за которую начинают
тянуть с постоянной силой F. Найти
угловые скорость и ускорение цилиндра,
если во время вращения на цилиндр
действует постоянный момент силы
трения Mтр.
12
13. Пример использования уравнения вращения твердого тела вокруг неподвижной оси
Направим ось Z от нас в плоскостьчертежа и запишем уравнение динамики
вращения твердого тела:
1
I z M z mR 2 z RF M тр
2
Тогда угловое ускорение цилиндра:
z
2( RF M тр )
mR 2
Угловая скорость цилиндра:
t
t
d z z dt z z dt
0
0
2( RF M тр )
mR
2
dt
2( RF M тр )
mR
2
t
13
14.
Теорема Гюйгенса – Штейнера14
15. Связь между моментами инерции твердого тела относительно двух параллельных осей, одна из которых проводит через центр масс
Мысленно разделим тело на частицымассами mi; к каждой частице
проведем радиусы-векторы ri и ri ,
перпендикулярные осям ZC и Z.
Учтем в дальнейшем, что ri = ri + b.
Момент инерции относительно оси Z:
2
2
2
I mi ri mi (ri b ) (mi ri 2mi ri b mi b 2 )
i
i
i
2
2
mi ri 2b mi ri b mi I C 2b mrC mb 2
i
i
i
15
16. Связь между моментами инерции твердого тела относительно двух параллельных осей, одна из которых проводит через центр масс
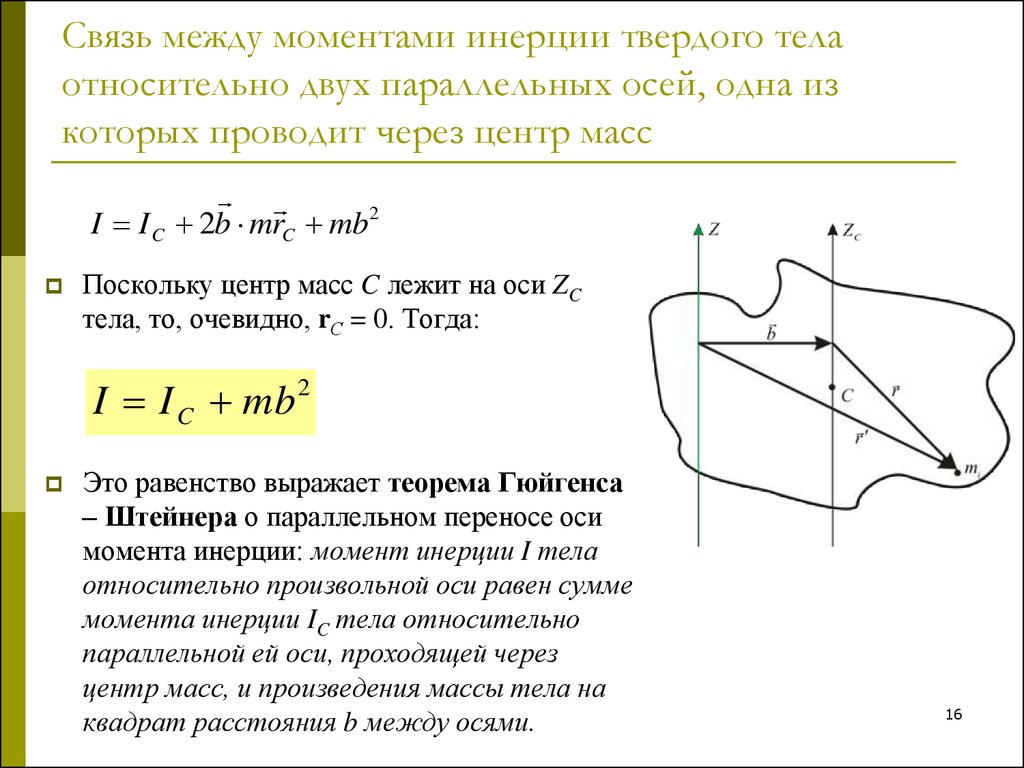
I I C 2b mrC mb2Поскольку центр масс C лежит на оси ZC
тела, то, очевидно, rС = 0. Тогда:
I I C mb 2
Это равенство выражает теорема Гюйгенса
– Штейнера о параллельном переносе оси
момента инерции: момент инерции I тела
относительно произвольной оси равен сумме
момента инерции IC тела относительно
параллельной ей оси, проходящей через
центр масс, и произведения массы тела на
квадрат расстояния b между осями.
16
17. Примеры использования теоремы Гюйгенса - Штейнера
Пример 1. Зная момент инерции тонкого стержня массы mи длины l относительно оси, перпендикулярной к стержню
и проходящей через его середину (центр масс) I =
(1/12)ml2, найдем момент инерции стержня относительно
параллельной оси, проходящей через один из концов
стержня:
2
1
1
1 2 1 2
l
2
2
2
I I C mb ml m ml ml ml
12
12
4
3
2
17
18. Примеры использования теоремы Гюйгенса - Штейнера
Пример 2. Зная момент инерции однородного шара массыm и радиуса R относительно оси, проходящей через его
центр (центр масс) I = (2/5)mR2, найдем момент инерции
шара относительно оси, касательной к поверхности шара:
2
7
2
2
I I C mb mR mR mR 2
5
5
2
18
19. ДИНАМИКА ТВЕРДОГО ТЕЛА
Кинетическая энергия и работавнешних сил при вращении твердого
тела вокруг неподвижной оси
19
20. Кинетическая энергия твердого тела
Пусть твердое тело вращается вокруг неподвижной оси Zс угловой скоростью . Разделим мысленно тело на
частицы массами mi.
Траекторией каждой из частиц является окружность с
центром на оси вращения, лежащая в перпендикулярной к
оси вращения плоскости. Обозначим скорость каждой из
частиц vi = Ri.
Кинетическая энергия твердого тела равна сумме
кинетических энергий составляющих его частиц:
mi vi2
mi ( Ri ) 2 2
2
2
2
i
i
2
I
2
m
R
i i i 2
20
21. Кинетическая энергия твердого тела
Таким образом, кинетическая энергия твердого тела,вращающегося вокруг неподвижной оси, равна:
I 2
2
Здесь I – момент инерции тела относительно оси
вращения.
21
22. Работа внешней силы при вращении твердого тела вокруг неподвижной оси
Пусть на вращающееся вокруг неподвижной оси Z твердоетело действует внешняя сила F, проекция на ось Z момента
M которой равна Mz. Найдем выражение для работы A силы,
снова рассматривая твердое тело как систему частиц.
По теореме о кинетической энергии элементарная работа A
всех сил, действующих на частицы, равна бесконечно
малому приращению кинетической энергии d системы:
A d
Примем без доказательства, что элементарная работа всех
внутренних сил равна нулю.
22
23. Работа внешней силы при вращении твердого тела вокруг неподвижной оси
Тогда теорема о кинетической энергии применительно ктвердому телу звучит так: работа всех приложенных к
твердому телу внешних сил равна приращению его
кинетической энергии:
Aвнеш d
I 2z
I 2
I z d z
d
d d
2
2
Согласно уравнению вращения твердого тела вокруг
неподвижной оси:
d z
I
M z ,внеш Id z M z ,внеш dt
dt
23
24. Работа внешней силы при вращении твердого тела вокруг неподвижной оси
Тогда элементарное приращение кинетической энергиитвердого тела:
d I z d z M z ,внеш z dt M z ,внеш
d
dt M z ,внеш d
dt
Здесь – угловая координата, d – угол, на который
поворачивается тело за бесконечно малый промежуток
времени dt.
Таким образом,
Aвнеш M z ,внеш d
Aвнеш M z ,внеш d
0
24
25. ДИНАМИКА ТВЕРДОГО ТЕЛА
Динамика плоского движения твердоготела
25
26. Плоское движения твердого тела
Напомним, что плоским движением твердого теланазывается такое движение, при котором все точки тела
перемещаются, оставаясь в параллельных друг другу
неподвижных плоскостях.
В качестве примера в дальнейшем рассмотрим движение
цилиндрического тела, скатывающегося по наклонной
плоскости.
Как уже было сказано ранее, плоское движение можно
рассматривать как совокупность двух видов движения:
поступательного движения вместе с произвольной точкой тела;
вращения вокруг оси, проходящей через эту точку.
26
27. Плоское движения твердого тела
В качестве такое точки рассмотрим центр масс тела. Тогда, всоответствии с теоремой о движении центра масс и
уравнением вращения твердого тела вокруг неподвижной
оси, проходящей через центр масс, можно записать:
dv C
m
F;
dt
I z M z
Здесь m – масса тела; vС – скорость центра масс; F – сумма
всех внешних сил, приложенных к телу; I – момент инерции
тела относительно оси вращения Z, проходящей через центр
масс; z – проекция на ось Z углового ускорения тела; Mz –
проекция на ось Z суммы моментов всех внешних сил.
27
























 physics
physics








