Similar presentations:
Кинематика точки. Способы задания движения. Уравнения движения. Траектория. Закон движения точки
1. Курс лекций по механике
Евразийский национальныйуниверситет им. Л.Н. Гумилева
Курс лекции по ФИЗИКЕ
МЕХАНИКА
Мухамедрахимова Г.И.
Курс лекций по
механике
Кинематика
Электронный учебный курс создан на основе лекций, читавшихся автором для студентов,
обучавшихся по инженерно-техническим специальностям г.Кокшетау и г.Астана (1981-2013 гг.).
Учебный материал соответствует календарным планам в объеме 1 семестра.
Для полной реализации анимационных эффектов при презентации необходимо использовать средство просмотра
Power Point не ниже, чем встроенный в Microsoft Office операционной системы Windows-ХР Professional.
Запуск презентации – F5, навигация – Enter, навигационные клавиши, щелчок мыши, кнопки.
Завершение – Esc.
Замечания и предложения можно послать по e-mail: isatai-07@miit.ru .
2. Содержание
Тема 1. Кинематика точки. Способы задания движения. Уравнения движения.Траектория. Закон движения точки. Связь между тремя способами задания движения.
Скорость точки.
Тема 2. Ускорение точки. Равнопеременное движение точки. Классификация движения
точки. Пример решения задач на определение кинематических характеристик движения
точки. Кинематика твердого тела. Виды движений. Поступательное движение.
Тема 3. Вращательное движение. Угловая скорость и угловое ускорение.
Равнопеременное вращение. Скорость и ускорение точки тела при вращательном
движении. Скорость и ускорение точки вращающегося тела как векторные произведения.
Формула Эйлера. Преобразование вращений.
Тема 4. Сферическое движение твердого тела. Теорема Эйлера. Угловая скорость и
угловое ускорение. Скорость и ускорение точки тела во сферическом движении. Общий
случай движения. Скорость точки свободного тела. Независимость векторов угловой
скорости и углового ускорения от выбора полюса. ускорение точки свободного тела.
Тема 5. Сложное движение точки. Теорема о сложении ускорений точки при сложном
движении. Теорема о сложении ускорений при сложном движении точки. Ускорение
Кориолиса. Причины возникновения ускорения Кориолиса.
Рекомендуемая литература
Основная литература
Трофимова Т.И.Курс физики. М.: Высшая школа, 1990.
Дж.Б.Мэрион. Курс физики. М., 1994.
Лаврова Т.И. Курс физики. - М.: Высшая школа, 1987.
Волькенштейн В.С. Сборник задач по общему курсу физики. – М.: Наука, 1990.
Чертов А.Г. и др. Задачник по физике (с примерами решения задач и справочными материалами) М.:Высшая школа, 1973.
Дополнительная литература
Линднер Г. Картины современной физики. - М.: Мир, 1977.
Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. М.: Мир. 1977.
Трофимова Т.И.Краткий курс физики. М.: Высшая школа, 2000.
Зисман Г.А., Тодес О.М. Курс общей физики. М.: Наука, 1974.
Трофимова Т.И., Павлова З.Г. Сборник задач по физике. М.: Высшая школа, 2003.
Балаш В.А. Задачи по физике и методы их решения. – М.: Просвещение, 1974.
3. Тема 1
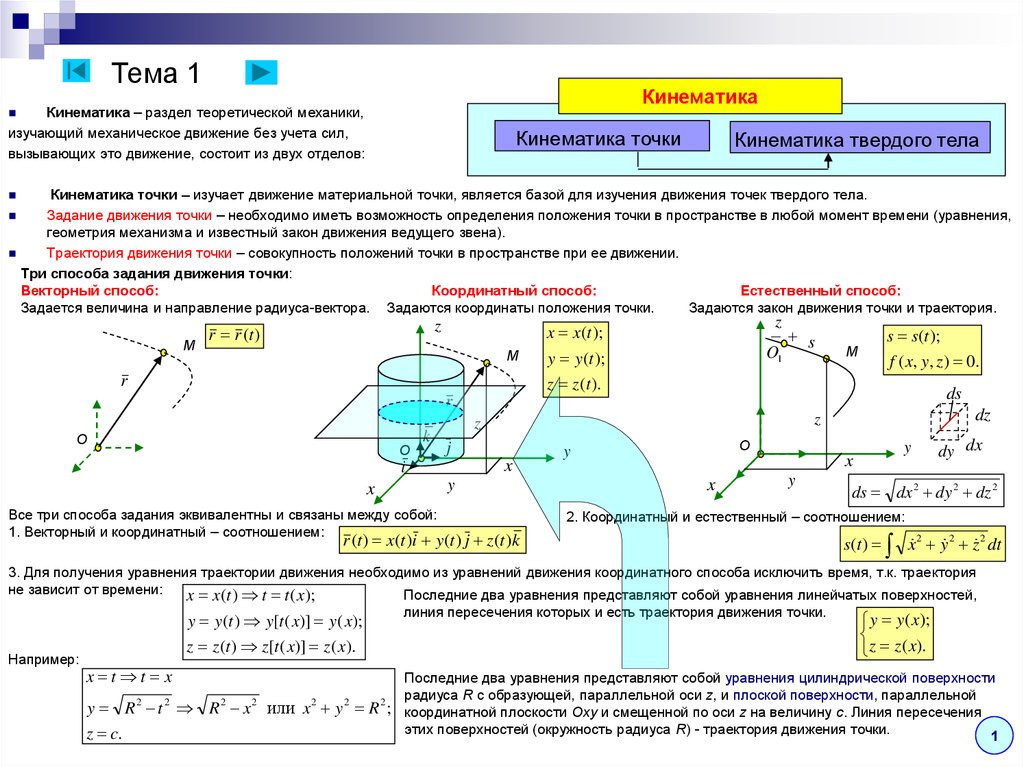
КинематикаКинематика – раздел теоретической механики,
изучающий механическое движение без учета сил,
вызывающих это движение, состоит из двух отделов:
Кинематика точки
Кинематика твердого тела
Кинематика точки – изучает движение материальной точки, является базой для изучения движения точек твердого тела.
Задание движения точки – необходимо иметь возможность определения положения точки в пространстве в любой момент времени (уравнения,
геометрия механизма и известный закон движения ведущего звена).
Траектория движения точки – совокупность положений точки в пространстве при ее движении.
Три способа задания движения точки:
Векторный способ:
Координатный способ:
Естественный способ:
Задаются закон движения точки и траектория.
Задается величина и направление радиуса-вектора. Задаются координаты положения точки.
M
z
r r (t )
M
r
z
s
O1
x x(t );
y y (t );
z z (t ).
s s(t );
M
f ( x, y, z ) 0.
ds
r
O
O
k
j
x
i
x
Все три способа задания эквивалентны и связаны между собой:
1. Векторный и координатный – соотношением:
dz
z
z
y
r (t ) x(t )i y(t ) j z (t )k
O
y
x
x
y
y
dy dx
ds dx 2 dy 2 dz 2
2. Координатный и естественный – соотношением:
s(t ) x 2 y 2 z 2 dt
3. Для получения уравнения траектории движения необходимо из уравнений движения координатного способа исключить время, т.к. траектория
не зависит от времени:
Последние два уравнения представляют собой уравнения линейчатых поверхностей,
x x(t ) t t ( x);
линия пересечения которых и есть траектория движения точки.
Например:
y y (t ) y[t ( x)] y ( x);
z z (t ) z[t ( x)] z ( x).
x t t x
y R2 t 2 R2 x2
z c.
y y( x);
z z ( x).
Последние два уравнения представляют собой уравнения цилиндрической поверхности
радиуса R c образующей, параллельной оси z, и плоской поверхности, параллельной
или x 2 y 2 R 2 ; координатной плоскости Oxy и смещенной по оси z на величину c. Линия пересечения
этих поверхностей (окружность радиуса R) - траектория движения точки.
1
4. Тема 1
Скорость точки – величина, характеризующая быстроту изменения положения точки в пространстве.Три способа задания движения точки определяют способы определения скорости точки:
Векторный способ: Сравним два положения точки в моменты времени t и t1= t + t:
t
r;
t1 t Δt r1 r Δr ;
M
v
Δr
r
M1 v
ср
O
dr
dt
- вектор средней скорости в интервале времени t,
направлен по направлению вектора перемещения (хорде MM1).
Предел отношения приращения функции
Δr dr
к приращению приращения аргумента есть Δt lim 0
Δt dt
производная функции (по определению):
- вектор истинной скорости точки в момент времени t, направлен по касательной к траектории
(при приближении M1 к M хорда занимает положение касательной).
Устремим t 0 и перейдем к пределу:
v
r1
Δr
vср
Δt
Δt
lim 0
Δr
v
Δt
r (t ) x(t )i y(t ) j z (t )k
Координатный способ: Связь радиуса-вектора с координатами определяется выражением:
z
vz
Используем векторную форму определения скорости:
M
dr (t ) d
vy v
x(t )i y (t ) j z (t )k Компоненты
Проекции
v x x ;
dt
dt
(составляющие) v x x(t )i ;
скорости
vx
вектора
r
v y y ;
v y y (t ) j; на оси
dx
dy
dz
i
j
k
v
i
v
j
v
k
скорости:
x
y
z
координат:
z
O
k
dt
j
x
i
x
v z z .
v z z (t )k .
dt
y
y
v x 2 y 2 z 2 ;
x
cos(v , x) ;
v
y
cos(v , y ) .
v
Используем векторную форму определения скорости:
Естественный способ:
O
dt
Представим радиус-вектор как сложную функцию: r (t ) r [ s (t )].
v
dr (t ) dr ds dr
s .
dt
ds dt ds
dr
Δr
Представим производную
lim 0
.
s M
радиус-вектора как предел: ds Δs
Вектор приращения радиуса-вектора направлен по хорде MM1
Δs
O1
и в пределе занимает положение касательной.
Δs v
Величина
производной
Δr
При s 0 радиус кривизны 1 , угол
M1
2 sin Δ2
dr
Δr
радиуса-вектора
lim
lim
1
.
между радиусами кривизны 0, числитель Δs
Δ
0
0
r
по дуговой координате равна 1: ds
Δs
Δ
- основание равнобедренного треугольника,
r1
знаменатель – длина круговой дуги радиуса .
Таким образом, производная радиуса-вектора по дуговой координате есть
единичный вектор, направленный по касательной к траектории.
Вектор скорости равен:
v s .
Проекция скорости на касательную:
При s 0 вектор скорости направлен в сторону увеличения дуговой
координаты, В противном случае – в обратную сторону.
v s .
Δr
Δ
1
Δs
2
5. Тема 2
Ускорение точки – величина, характеризующая быстроту изменения скорости точки.t
v;
Три способа задания движения точки определяют способы определения ускорения точки:
Векторный способ: Сравним скорости точки в двух положениях точки в моменты времени t и t1= t + t:
t1 t Δt v1 v Δv ;
M
Δv
v
v
- вектор среднего ускорения в интервале времени t, направлен в сторону вогнутости траектории.
a
Δr
r
O
v1
a
r1
Δt
M1
v
v1
a
ср
Переходя к пределу получаем:
dv d 2 r
dt dt 2
Δt lim 0
Δv
a
Δt
Δt
lim 0
Δ v dv
Δt
dt
- вектор истинного ускорения точки в момент времени t, лежит в
соприкасающейся плоскости (предельное положение плоскости, проведенной
через касательную в точке M и прямую, параллельную касательной в точке M1, при
стремлении M1 к M) и направлен в сторону вогнутости траектории.
Координатный способ: Используем полученное векторное выражение и связь радиуса-вектора с координатами
z
az
M
ay
r
O
i
k
ax
z
j
x
d 2 r (t ) d 2
a
2 x(t )i y (t ) j z (t )k
dt 2
dt
2
2
d x
d y
d 2z
2 i 2 j 2 k axi a y j az k
dt
dt
dt
Компоненты
(составляющие)
вектора
ускорения:
y
a x x i ;
a y y j;
a z z k .
Проекции
ускорения
на оси
координат:
r (t ) x(t )i y(t ) j z (t )k
a x 2 y 2 z 2 ;
a x x ;
x
a y y ; cos( a , x) ;
a
a z z .
y
cos( a , y ) .
a
y
Таким образом полное ускорение точки есть векторная сумма двух ускорений:
Естественный способ: Используем векторное выражение для ускорения и выражение для скорости при естественной способе задания: v s .
касательного, направленного по касательной к траектории в сторону увеличения
дуговой координаты,
если s 0 (в противном
случаеединичного
– в противоположную)
d d dsи
d
dv d
d
Представим
единичный
Производная
s M
s .
a
( s ) s s
. касательный
(
t
)
[
s
(
t
)].
нормального
ускорения,
направленного
по
нормали
к
касательной
в сторону
центра
вектор
касательного
вектора:
Δs
dt dt
dt
O1
dt
ds dt
ds
кривизны
(вогнутости
avτ
как
сложную
функцию: траектории): a a a .
τ
n
n
Величина производной
Таким образом, производная
M1
a n Δr
единичного касательного вектора d
2 sin Δ2 2 1 2единичного касательного вектора
Δ
Модуль
r
Δs полного
lim 0 ускорения:
Δ lim 0 a a τ .an по; дуговой координате есть вектор,
по дуговой координате:
a
ds
Δs
Δ
направленный перпендикулярно
r1
Приединичный
s 0 радиус
кривизны
1 , угол
Угол между приращением касательной к траектории.
Введем
вектор
n, нормальный
(перпендикулярный)
к касательной,
O
a s ;
1
между радиусами
единичного вектора
направленный
к центрукривизны
кривизны. 0, числитель Компоненты
Δs
a τ s ;
Δr
Проекции
2
-основание
равнобедренного
треугольника,
и
самим
вектором
2
С использованием вектора n и ранее
s (составляющие)
s
о
2
образованного
единичными векторами 1 и a
, s Δ
при 0, стремится
n . вектора
определенных
величин
a n кn90
. . ускорения a s .
3
знаменатель
–
длина
круговой
дуги
радиуса
.
на
оси
и
n:
1
ускорение представляется как сумма векторов:
n
ускорения:
x
1
6. Тема 2
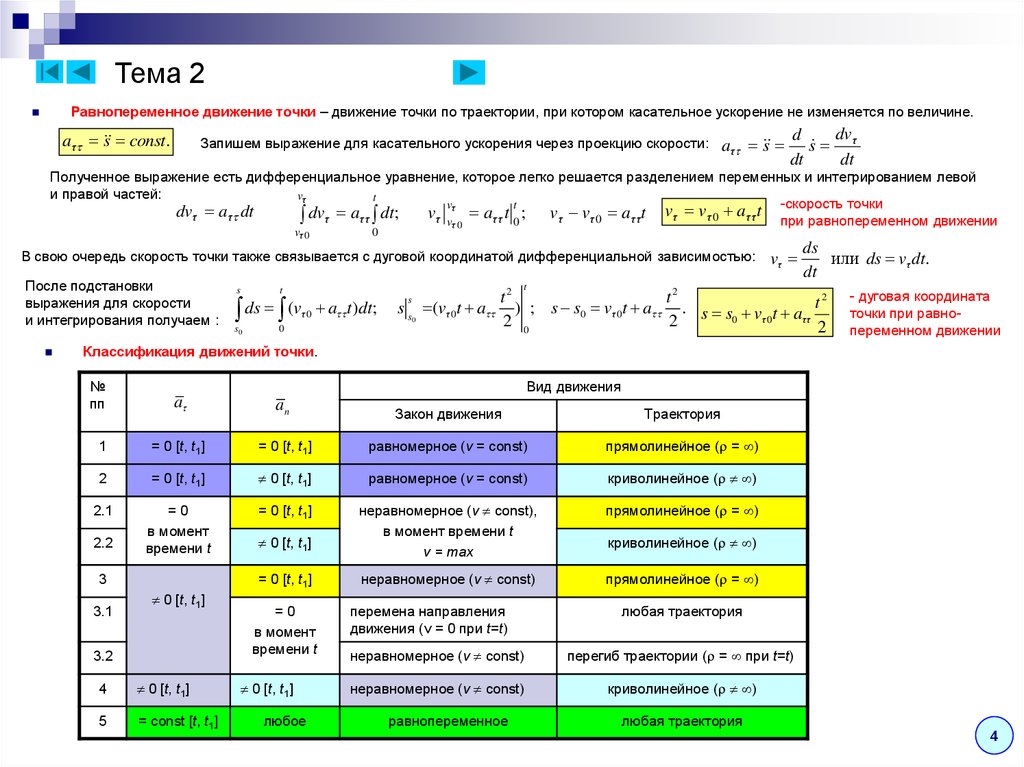
Равнопеременное движение точки – движение точки по траектории, при котором касательное ускорение не изменяется по величине.a τ s const.
Запишем выражение для касательного ускорения через проекцию скорости:
a τ s
dv
d
s τ
dt
dt
Полученное выражение есть дифференциальное уравнение, которое легко решается разделением переменных и интегрированием левой
и правой частей:
vτ
t
v
t
-скорость точки
dv τ a τ dt
dv
a
v τ vτ a ττ t 0 ; v τ v τ 0 a ττt v τ v τ 0 a τ τt при равнопеременном движении
τ
ττ dt ;
τ0
vτ 0
0
В свою очередь скорость точки также связывается с дуговой координатой дифференциальной зависимостью: vτ
После подстановки
выражения для скорости
и интегрирования получаем :
s
t
t
ds (v
τ0
s0
a t )dt;
0
s
ss
0
ds
или ds vτ dt.
dt
2
t2
t2
(vτ 0t a ) ; s s0 vτ 0t a . s s v t a t
0
τ0
ττ
2 0
2
2
- дуговая координата
точки при равнопеременном движении
Классификация движений точки.
№
пп
Вид движения
a
an
Закон движения
Траектория
1
= 0 [t, t1]
= 0 [t, t1]
равномерное (v = const)
прямолинейное ( = )
2
= 0 [t, t1]
0 [t, t1]
равномерное (v = const)
криволинейное ( )
2.1
=0
в момент
времени t
= 0 [t, t1]
прямолинейное ( = )
0 [t, t1]
неравномерное (v const),
в момент времени t
v = max
= 0 [t, t1]
неравномерное (v const)
прямолинейное ( = )
2.2
3
3.1
0 [t, t1]
3.2
4
0 [t, t1]
5
= const [t, t1]
=0
в момент
времени t
0 [t, t1]
любое
перемена направления
движения (v = 0 при t=t)
криволинейное ( )
любая траектория
неравномерное (v const)
перегиб траектории ( = при t=t)
неравномерное (v const)
криволинейное ( )
равнопеременное
любая траектория
4
7. Тема 2
Кинематика твердого тела – изучает движение твердого тела, кинематика точки используется для получения новых зависимостей иформул.
Существует пять видов движения твердого тела:
1. Поступательное (ползун, поршень насоса, спарник колес паровоза, движущегося по прямолинейному пути, кабина лифта, дверь купе,
кабина колеса обозрения).
2. Вращательное (маховик, кривошип, коромысло, колесо обозрения, обычная дверь).
3. Плоскопараллельное или плоское (шатун, колесо локомотива при качении по прямолинейному рельсу, шлифовальный круг).
4. Сферическое (гироскоп, шаровая стойка).
5. Общий случай движения или свободный полет (пуля, камень, небесное тело)
Поступательное движение твердого тела – такое движение при котором любая прямая, жестко связанная с телом, остается
параллельной самой себе. Обычно поступательное движение отождествляется с прямолинейным движением его точек, однако это не
так. Точки и само тело (центр масс тела) могут двигаться по криволинейным траекториям, см. например, движение кабины колеса
обозрения.
Теорема о поступательном движении твердого тела – При поступательном движении твердого тела все его точки описывают
тождественные траектории и имеют в каждый момент времени геометрически равные скорости и ускорения.
Проведем радиус-векторы к двум точкам A и B, а также соединим эти точки вектором rBA.
В любой момент времени выполняется векторное равенство:
В любой момент времени вектор rBA остается постоянным по направлению
(по определению поступательного движения) и по величине
rA (t ) rB (t ) const ,
(расстояние между точками не изменяется).
Отсюда:
и это означает, что в каждый момент времени положение точки A отличается от положения
Таким
твердого
тела полностью
точкиобразом,
B на однупоступательное
и ту же величинудвижение
rBA = const,
т.е. траектории
этих двух определяется
точек тождественны
движением
одной
точки,
принадлежащей
этому
телу
и
выбранной
произвольным образом.
(совпадают друг с другом при наложении).
Все параметры движения этой точки (траектория, скорость и ускорение) описываются
drA (t ) drB (t )
уравнениями
и соотношениями
кинематики
точки.часть соотношения:
Продифференцируем
по времени
левую и правую
vA
A
aA
rA
rA
rBA
rBA
vB
dt
B
rB
rB
C
rA (t ) rB (t ) rBA.
aB
dt
и это означает, что в каждый момент времени скорость точки A равна геометрически
(т.е. векторно) скорости точки B.
v (t ) v (t ).
A
B
Второе дифференцирование по времени приводит к соотношению:
dr 2 A (t ) dr 2 B (t )
dt 2
dt 2
и это означает, что в каждый момент времени ускорение точки A равно геометрически
(т.е. векторно) ускорению точки B.
aA (t ) aB (t ).
5
8. Тема 3
Вращательное движение твердого тела – движение при котором все его точки движутся в плоскостях, перпендикулярных некоторойнеподвижной прямой, и описывают окружности с центрами, лежащими на этой прямой, называемой осью вращения.
Задание вращательное движения – движение задается законом изменения двугранного угла
φ (угла поворота), образованного неподвижной плоскостью P, проходящей через ось
вращения, и плоскостью Q, жестко связанной с телом:
(t ) - уравнение вращательного движения
P
ω
ε
Угловая скорость – величина, характеризующая быстроту изменения угла поворота.
t
;
t1 t Δt 1 Δ ;
Q
Δ
ср - средняя угловая скорость в интервале времени t,
Δt
Устремим t 0 и перейдем к пределу:
Δt
lim 0
Δ
d
Δt
dt
Если dφ/dt > 0, то вращение происходит в сторону увеличения угла поворота,
если dφ/dt < 0, то вращение происходит в сторону уменьшения угла поворота.
Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости.
t
;
t1 t Δt 1 Δ ;
Δ
ср - среднее угловое ускорение в интервале времени t,
Δt
d
- истинное угловое ускорение
Δ
Устремим t 0 и перейдем к пределу: Δt lim 0
в момент времени t
dt
Δt
- истинная угловая скорость
в момент времени t
Угловая скорость
изображается дуговой
стрелкой в сторону
вращения.
Угловое ускорение
изображается дуговой
стрелкой в сторону
увеличения угла поворота
при
0 .
Если d2φ/dt2 и dφ/dt одного знака, то скорость увеличивается по модулю и вращение называется ускоренным (дуговые стрелки угловой скорости
и углового ускорения направлены в одну сторону),
если d2φ/dt2 и dφ/dt разного знака, то скорость уменьшается по модулю и вращение называется замедленным (дуговые стрелки угловой скорости
и углового ускорения направлены в противоположные стороны).
const.
Равномерное вращение – угловая скорость не изменяется по величине.
Равнопеременное вращение – угловое ускорение не изменяется по величине.
const.
d
;
dt
t
0
0
d dt;
0 t.
d
;
dt
d
;
dt
t
0
0
t
0
0
d dt;
d ( 0 t )dt;
0 t.
0 0t
t2
.
2
6
9. Тема 3
Скорость точки при вращательном движении твердого тела – траектория точки известна (окружность радиуса R – расстояние точкидо оси вращения), можно применить формулу для определения скорости точки при естественном задании движения:
v s .
Дуговая координата связана
с радиусом окружности:
- O
+
s
R
φ
ε
aanос
aaврτ
ω
a
v
s R.
Тогда проекция скорости
на касательную к окружности:
vτ
d
d
( R)
R R.
dt
dt
Поскольку далее работают с модулем угловой скорости после изображения ее
в виде дуговой стрелки расчетной формулой является выражение для модуля скорости: v R
и вектор скорости направляют перпендикулярно радиусу
в сторону дуговой стрелки угловой скорости.
Как следует из формулы скорость точки пропорциональна расстоянию ее до оси вращения (радиусу вращения).
Тогда проекции ускорения
на касательную
aτ
к окружности и нормаль:
Ускорение точки при вращательном движении твердого тела – траектория точки известна, можно применить
формулы для определения ускорений точки при естественном задании движения:
s 2
a τ s ; a n
d2
d 2
(
R
)
R R.
dt 2
dt 2
1 d
1 d
(
R
)
dt
R dt
2
an
2
R 2 R.
.
Поскольку далее работают с модулем углового ускорения после изображения его в виде дуговой стрелки расчетной формулой является
выражение для касательного ускорения: a R и вектор этого ускорения, называемого вращательным ускорением, направляют
вр
перпендикулярно радиусу в сторону дуговой стрелки углового ускорения.
z
z
Нормальное ускорение теперь называется осестремительным ускорением aос R , его направляют по радиусу
к оси вращения
независимо от направления дуговой стрелки угловой скорости, не говоря уж о направлении дуговой стрелки углового ускорения.
2
ω
Как следует из формул оба ускорения точки пропорциональны расстоянию ее до оси вращения (радиусу вращения).
ω
Угол между направлением полного ускорения и
радиусом от величины радиуса не зависит
ε и
ε
равен:
aвр
Скорость и ускорения точки при вращательном движении как векторные произведения.
arctg arctg 2 .
Представим угловую скорость и угловое ускорения как векторы, направленные по оси вращения в ту
aос
сторону, откуда дуговые стрелки этих величин указывают вращение против часовой стрелки.
Полное ускорение точки, как и ранее, есть векторная сумма этих ускорений:
a a вр a ос .
Положительное направление оси z можно задать с помощью единичного вектора k, тогда
векторы угловой скорости и углового ускорения можно представить как:
z k z k
где z, z – проекции соответствующих векторов на ось z.
k
k
7
10. Тема 3
Скорость точки при вращательном движении как векторное произведение – определяется выражениемописывает и величину, и направление скорости.
Величина (модуль) этого
Таким образом:
v 1 r sin( , r ).
векторного произведения:
ω
, которое
v R.
2 произведения:
Направление вектора рассматриваемого векторного
по определению векторного произведения – перпендикулярноRплоскости, проведенной через умножаемые вектора,
направлен в ту сторону, откуда поворот первого вектора ко второму на наименьший угол кажется происходящим
против часовой стрелки;
по правилу правой руки – при совмещении большого пальца с первым вектором, остальных – со вторым вектором,
поворот большого пальца перпендикулярно ладони указывает на направление вектора векторного произведения.
R
r
v r
v
Таким образом, действительно векторное произведение угловой скорости и радиус-вектора полностью определяет
величину и направление скорости точки при вращательном движении в соответствии с ранее полученными результатами.
Вращательное ускорение точки как векторное произведение – определяется выражением
описывает и величину, и направление вращательного ускорения.
ε
R
r
aвр r
, которое
Таким образом:
Величина (модуль) этого векторного a
aвр R.
вр r sin( , r ).
произведения:
Направление вектора рассматриваемого векторного произведения можно установить по определению векторного
произведения или по правилу правой руки.
R
образом, действительно векторное произведение углового ускорения и радиус-вектора полностью определяет
a вр Таким
величину и направление вращательного ускорения точки в соответствии с ранее полученными результатами.
Осестремительное ускорение точки как векторное произведение – определяется
выражением a v , которое описывает и величину, и направление осестремительного
ос
ускорения.
Величина (модуль) этого
векторного произведения:
aос v sin( , v ).
Таким образом:
v v ( R) 2 R.
Направление вектора рассматриваемого векторного произведения можно установить по определению векторного
произведения или по правилу правой руки.
1, т.к. вектор скорости точки перпендикулярен плоскости,
Таким образом, действительно векторное произведение угловой
скорости
и вектора
скорости
точки полностью
в которой
лежит
вектор угловой
скорости.
определяет величину и направление осестремительного ускорения точки в соответствии с ранее полученными
результатами.
Это векторное произведение может быть также записано в виде: a ( r )
ос
ω
R
r
a ос
v
8
11. Тема 3
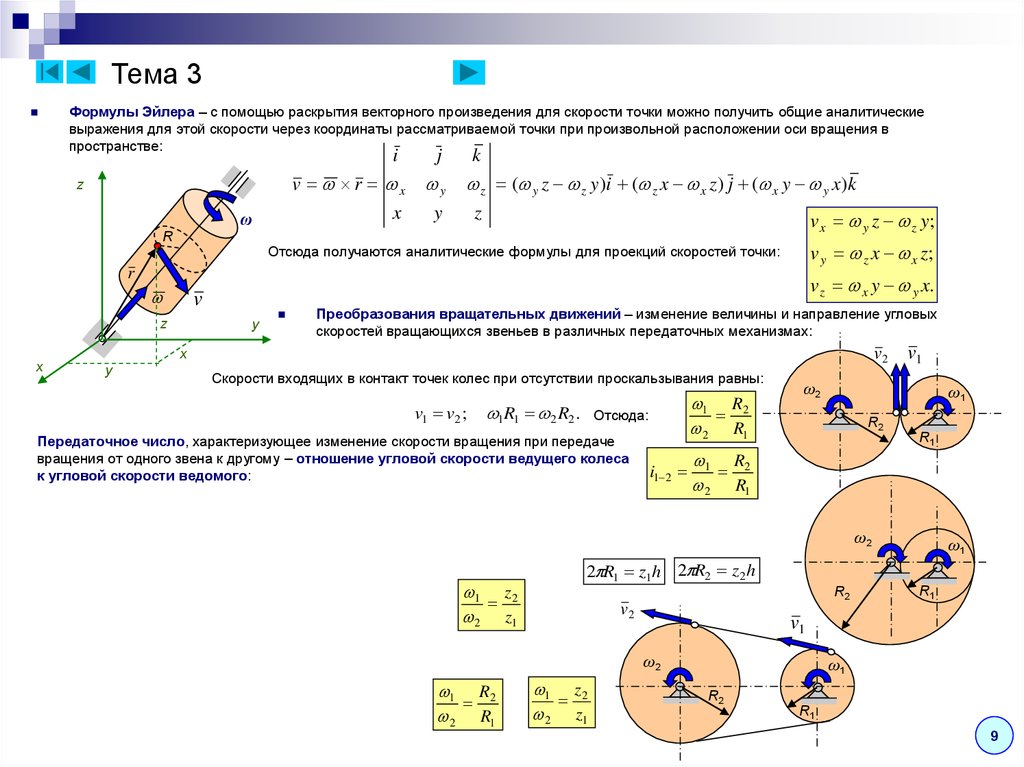
Формулы Эйлера – с помощью раскрытия векторного произведения для скорости точки можно получить общие аналитическиевыражения для этой скорости через координаты рассматриваемой точки при произвольной расположении оси вращения в
пространстве:
i
v r x
z
x
ω
R
j
k
y z ( y z z y )i ( z x x z ) j ( x y y x)k
y
z
v x y z z y;
v y z x x z;
Отсюда получаются аналитические формулы для проекций скоростей точки:
r
z
x
v z x y y x.
v
y
Преобразования вращательных движений – изменение величины и направление угловых
скоростей вращающихся звеньев в различных передаточных механизмах:
v2
x
y
Скорости входящих в контакт точек колес при отсутствии проскальзывания равны:
v1 v2 ;
1R1 2 R2 .
1 R2
2 R1
Отсюда:
Передаточное число, характеризующее изменение скорости вращения при передаче
вращения от одного звена к другому – отношение угловой скорости ведущего колеса
к угловой скорости ведомого:
i1 2
v1
ω2
ω1
R2
1 R2
2 R1
R1
ω2
1 z 2
2 z1
2 R1 z1h 2 R2 z 2 h
R2
v2
1 z 2
2 z1
R1
v1
ω2
1 R2
2 R1
ω1
ω1
R2
R1
9
12. КОНТРОЛЬ
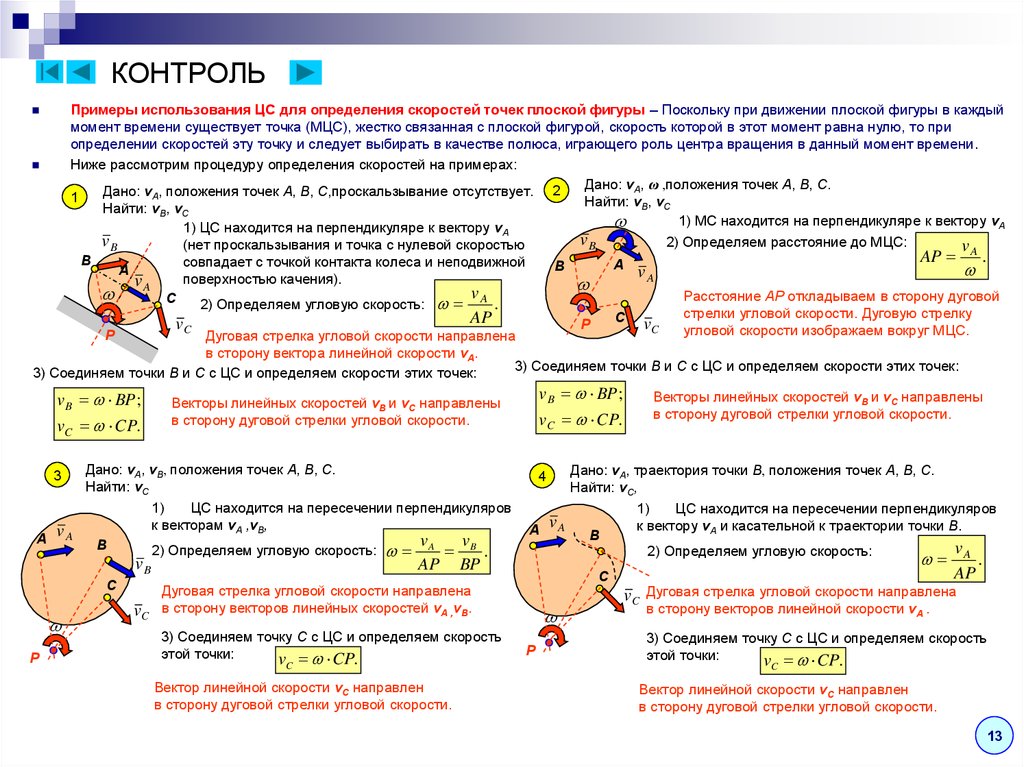
Примеры использования ЦС для определения скоростей точек плоской фигуры – Поскольку при движении плоской фигуры в каждыймомент времени существует точка (МЦС), жестко связанная с плоской фигурой, скорость которой в этот момент равна нулю, то при
определении скоростей эту точку и следует выбирать в качестве полюса, играющего роль центра вращения в данный момент времени.
Ниже рассмотрим процедуру определения скоростей на примерах:
Дано: vA, ω ,положения точек A, B, C.
Дано: vA, положения точек A, B, C,проскальзывание отсутствует. 2
1
Найти: vB, vC
Найти: vB, vC
1) МС находится на перпендикуляре к вектору vA
1) ЦС находится на перпендикуляре к вектору vA
vB
vB
2) Определяем расстояние до МЦС:
(нет проскальзывания и точка с нулевой скоростью
v
AP A .
B
совпадает с точкой контакта колеса и неподвижной
A
B
A
vA
поверхностью качения).
vA
v
Расстояние AP откладываем в сторону дуговой
C
2) Определяем угловую скорость: A .
стрелки угловой скорости. Дуговую стрелку
C
AP
vC угловой скорости изображаем вокруг МЦС.
vC
P
P
Дуговая стрелка угловой скорости направлена
в сторону вектора линейной скорости vA.
3) Соединяем точки B и C с ЦС и определяем скорости этих точек:
v B BP ;
vC CP.
Дано: vA, vB, положения точек A, B, C.
Найти: vC
1)
ЦС находится на пересечении перпендикуляров
к
векторам
vA ,vB,
v
A A
v
v
B
2) Определяем угловую скорость: A B .
vB
P
vC
v B BP ;
Векторы линейных скоростей vB и vC направлены
в сторону дуговой стрелки угловой скорости.
3
C
3) Соединяем точки B и C с ЦС и определяем скорости этих точек:
AP
BP
vC CP.
Дано: vA, траектория точки B, положения точек A, B, C.
Найти: vC,
1)
ЦС находится на пересечении перпендикуляров
v
к вектору vA и касательной к траектории точки B.
A A
B
vA
2) Определяем угловую скорость:
4
C
Дуговая стрелка угловой скорости направлена
в сторону векторов линейных скоростей vA ,vB.
3) Соединяем точку C с ЦС и определяем скорость
этой точки:
v CP.
C
Вектор линейной скорости vC направлен
в сторону дуговой стрелки угловой скорости.
Векторы линейных скоростей vB и vC направлены
в сторону дуговой стрелки угловой скорости.
P
AP
.
vC Дуговая стрелка угловой скорости направлена
в сторону векторов линейной скорости vA .
3) Соединяем точку C с ЦС и определяем скорость
этой точки:
v CP.
C
Вектор линейной скорости vC направлен
в сторону дуговой стрелки угловой скорости.
13
13. Тема 4
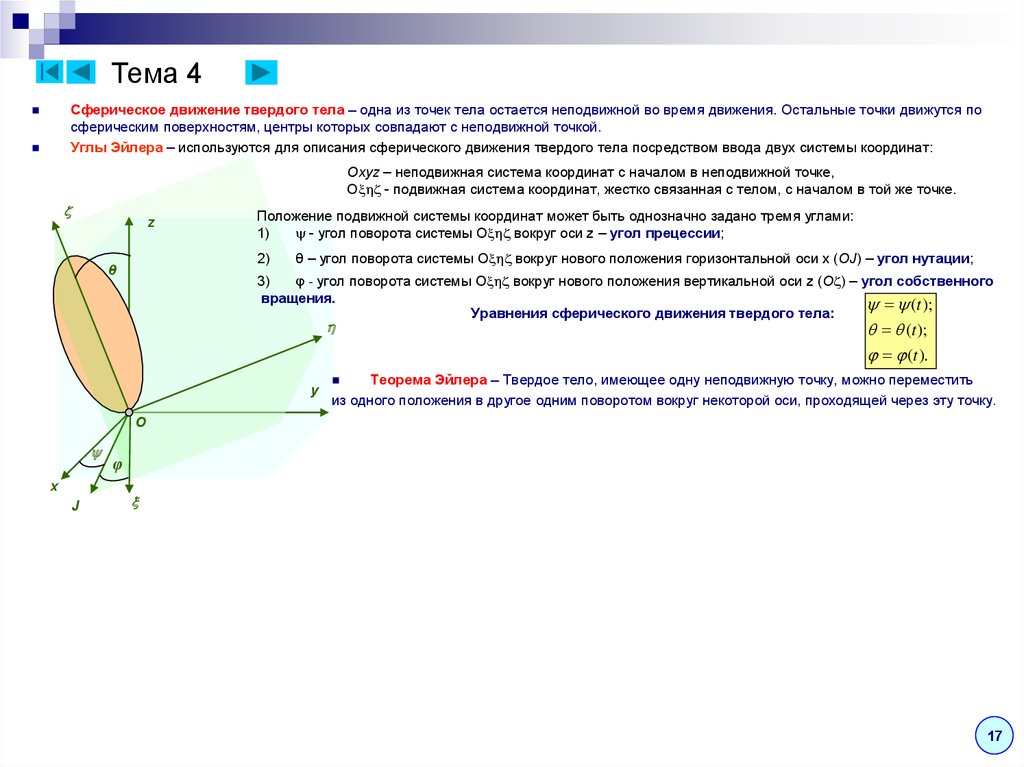
Сферическое движение твердого тела – одна из точек тела остается неподвижной во время движения. Остальные точки движутся посферическим поверхностям, центры которых совпадают с неподвижной точкой.
Углы Эйлера – используются для описания сферического движения твердого тела посредством ввода двух системы координат:
Oxyz – неподвижная система координат с началом в неподвижной точке,
O - подвижная система координат, жестко связанная с телом, с началом в той же точке.
z
Положение подвижной системы координат может быть однозначно задано тремя углами:
1)
- угол поворота системы O вокруг оси z – угол прецессии;
2)
θ
θ – угол поворота системы O вокруг нового положения горизонтальной оси x (OJ) – угол нутации;
3)
φ - угол поворота системы O вокруг нового положения вертикальной оси z (O ) – угол собственного
вращения.
(t );
Уравнения сферического движения твердого тела:
y
(t );
(t ).
Теорема Эйлера – Твердое тело, имеющее одну неподвижную точку, можно переместить
из одного положения в другое одним поворотом вокруг некоторой оси, проходящей через эту точку.
O
x
J
φ
17
14. Тема 5
■Причины возникновения ускорения Кориолиса: Формально ускорение Кориолиса было выведено группировкой слагаемых произведений,
содержащих проекции относительной скорости и производные по времени от ортов подвижной системы координат. При этом ранее было получено
удвоенное число таких слагаемых.
Для прояснения физических причин возникновения ускорения Кориолиса рассмотрим качественный пример, в котором специально будем
полагать постоянными вектор относительной скорости (в подвижной системе координат) и вектор угловой переносной скорости (вращения
подвижной системы координат относительно неподвижной оси):
Пусть в некоторый момент времени положение точки и вектора относительной и переносной скоростей таковы, как они изображены н
рисунке (вид сверху):
ve
vr
ve
vr
ωe
ωe
Через некоторое время точка удалится от оси вращения и тело повернется
на некоторый угол.
В результате:
1)
относительная скорость изменится по направлению из-за наличия
переносной угловой скорости и
2)
переносная линейная скорость изменится по величине из-за
наличия относительной скорости, изменяющей расстояние точки до
оси вращения.
Таким образом, можно считать что существует две причины возникновения
ускорения Кориолиса:
1) переносная угловая скорость влияет на относительную скорость, a
2) относительная скорость в свою очередь влияет на переносную линейную скорость.
Возможно, это поможет запомнить коэффициент, равный двум, в формуле,
определяющей ускорение Кориолиса.
c
r
■
Примеры определения направления ускорения Кориолиса
удобно рассмотреть для случаев различного положения движущихся
точек по поверхности Земли, вращающейся относительно своей оси:
a 2( e v ).
vr
vr
ac
ac
a
vr
c
vr
vr
e
23









 physics
physics








