Кинематика. Основные понятия. Траектория. Средняя и мгновенная скорости. Ускорение. Закон равноускоренного движения

1. Общая физика Механика Кинематика

2. Лекция 1. Кинематика. Основные понятия. Траектория. Средняя и мгновенная скорости. Ускорение. Закон равноускоренного движения.

Тело размерами, которого можно пренебречь в
условиях данной задачи называется материальной
точкой.
Тело относительно, которого происходит
определение положения рассматриваемого нами
тела, называется телом отсчета.
Абсолютно упругое тело – деформация которого
подчиняется закону Гука, а после прекращения
внешнего воздействия такое тело полностью
восстанавливает свои первоначальные размеры и
форму.
Абсолютно неупругое тело – полностью сохраняющее
деформированное состояние после прекращения
действия внешних сил.

3. Лекция 1. Кинематика. Основные понятия. Траектория. Средняя и мгновенная скорости. Ускорение. Закон равноускоренного движения.

Тело относительно, которого происходит
определение положения рассматриваемого нами
тела, называется телом отсчета.
Совокупность тела отсчета, связанной с ним
координатной системы и синхронизированных между
собой часов образует систему отсчета.

4. Кинематика.

Положение материальной точки в пространстве
можно определитьс помощью радиус вектора.
Радиус вектор r – это вектор проведенный из
начала координат системы отсчета в место где
находится материальная точка в данный момент
времени
При движении радиус вектор материальной точки
изменяется как по модулю, так и по направлению
r(t).
Геометрическое место концов радиуса вектора r
называется траекторией движения материальной
точки

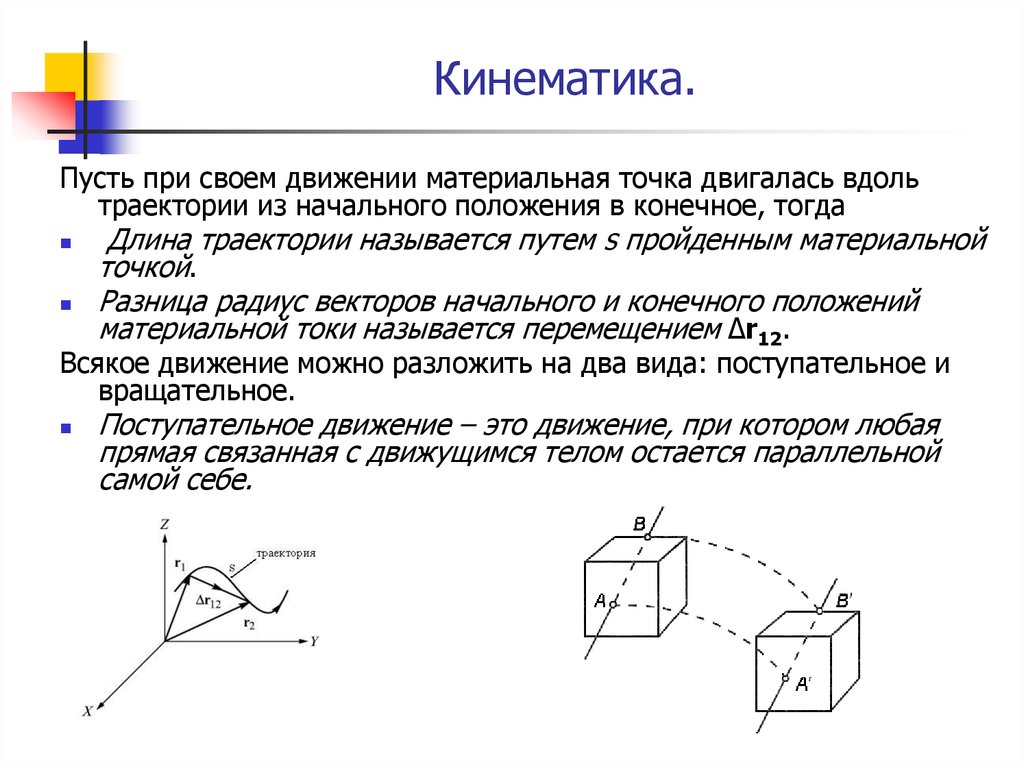
5. Кинематика.

Пусть при своем движении материальная точка двигалась вдоль
траектории из начального положения в конечное, тогда
Длина траектории называется путем s пройденным материальной
точкой.
Разница радиус векторов начального и конечного положений
материальной токи называется перемещением Δr12.
Всякое движение можно разложить на два вида: поступательное и
вращательное.
Поступательное движение – это движение, при котором любая
прямая связанная с движущимся телом остается параллельной
самой себе.

6. Кинематика

В случае вращательного движения все точки тела движутся по
окружностям центры, которых лежат на одной прямой,
называемой осью вращения.
Ось вращения может находиться и вне тела.
При движении материальной точки за время Δt из
начального положения в конечное ее
перемещение составляет величину Δr.
Тогда отношение Δr/Δt называют средним
вектором скорости (средней скоростью) <v> за
время Δt.
При стремлении Δt к нулю средний вектор скорости <v> стремится к
определенному пределу – этот предел называется скоростью
материальной точки (или мгновенной скоростью) в данный момент
времени v.
r dr
v lim
t 0 t
dt

7. Кинематика

Модуль вектора скорости v определяется следующим способом
dr
r
v = v lim
lim
t 0 t
t 0 dt

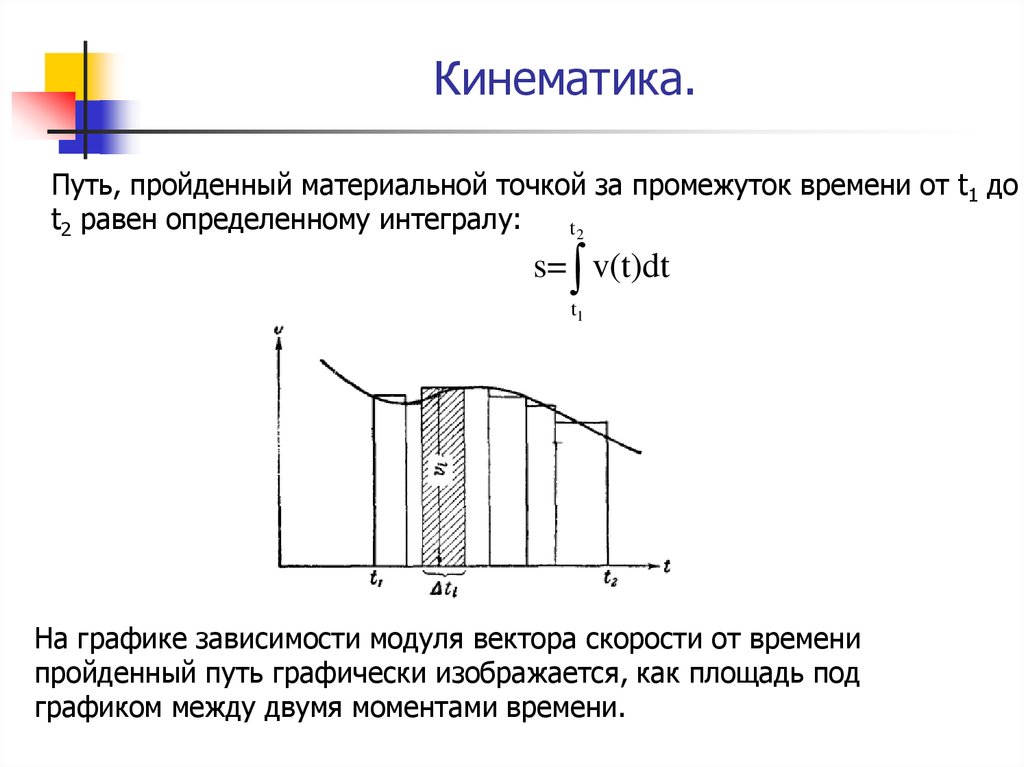
8. Кинематика.

Путь, пройденный материальной точкой за промежуток времени от t1 до
t2 равен определенному интегралу:
t2
s= v(t)dt
t1
На графике зависимости модуля вектора скорости от времени
пройденный путь графически изображается, как площадь под
графиком между двумя моментами времени.

9. Кинематика.

Движение материальной точки характеризуется также ускорением.
Вектор ускорения w определяет скорость изменения вектора скорости
материальной точки со временем, т.е равен производной от вектора
скорости по времени:
v dv d 2r
w = lim
2
t 0 t
dt dt
Прямолинейное движение с постоянным ускорением называется
равнопеременным.
В зависимости от поведения скорости со временем различают
равномерно-ускоренное и равномерно-замедленно движения.

10. Кинематика.

Зная, проекции радиус вектора r(t) на оси X, Y, Z декартовой
системы координат связанной с телом отсчета: x=x(t), y=y(t),
z=z(t), можно получить координатное представление радиус
вектора:
r (t) = x(t)e x +y(t)e y +z(t)e z
Взяв производную по времени от
выражения для радиус вектора, получим:
v=
dr dx
dy
dz
e x e y ez v x e x v ye y vzez
dt dt
dt
dt
Аналогично получаем координатное выражение
для ускорения w
dv y
dvz d 2 x
dv dvx
d2 y
d2 z
w=
ex
ey
e z 2 e x 2 e y 2 e z w x e x w ye y w z e z
dt dt
dt
dt dt
dt
dt

11. Кинематика.

Для полного решения задачи о движении материальной точки –
определения ее скорости v и положения r в зависимости от времени – не
достаточно знать зависимость w(t), еще необходимо знать и начальные
условия.
Рассмотрим случай движения материальной точки с постоянным
ускорением w=const.
t
Δv w.dt=wt
0
v=v0+Δv
v=v0 +wt
t
2
w
t
Δr = v (t)dt=v 0 t+
0
r=r0+Δr
2
w
t
r =r0 +v 0 t+
2
2

12. Лекция 2 Движения тела по окружности. Угловая скорость, нормальное и тангенициальное ускорение. Движение по окружности.

Введем единичный вектор τ, связанный с движущейся материальной
точкой и направленный по касательной к траектории в сторону скорости.
Вектор скорости v материальной точки направлен по касательной к траектории,
поэтом его можно определить следующим образом:
v=vτ τ
При стремлении начальной и конечной точек траектории друг к другу отрезок
траектории между ними стремится к дуге окружности с центром в некоторой
точке. Эту точку называют центром кривизны траектории в данной точке, а
радиус R соответствующей окружности - радиусом кривизны траектории в
данной точке

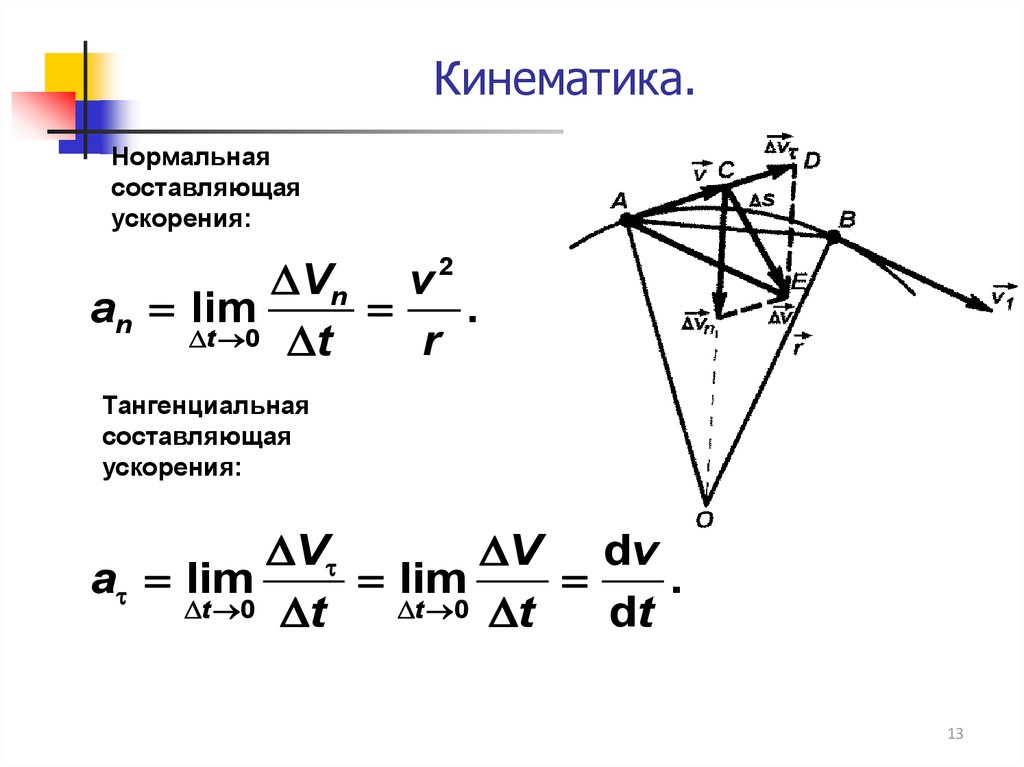
13.

Кинематика.
Нормальная
составляющая
ускорения:
Vn v 2
an lim
.
t 0 t
r
Тангенциальная
составляющая
ускорения:
V
V dv
a lim
lim
.
t 0 t
t 0 t
dt
13

14.

Кинематика.
Тангенциальное ускорение характеризует изменение скорости по
величине. Если скорость по величине не изменяется,
тангенциальное ускорение равно нулю. Нормальное ускорение
характеризует изменение скорости по направлению. Если
направление скорости не изменяется, движение происходит по
прямолинейной траектории.
Полное ускорение тела есть
геометрическая сумма тангенциальной
и нормальной составляющих:
dv
a
a an .
dt
a a a
2
n
2
14

15.

Кинематика.
В зависимости от тангенциальной и нормальной
составляющих ускорения движение можно
классифицировать следующим образом:
1) a 0;
an 0
— прямолинейное равномерное
движение;
2) a a const; an 0
При таком виде движения:
— прямолинейное
равнопеременное движение.
dv v 2 v 1
a a
.
dt
t 2 t1
15

16.

Кинематика.
3) a f (t ); an 0
4) a 0; an const
5) a 0; an 0
6) a const; an 0
7) a f (t ); an 0
— прямолинейное движение с
переменным ускорением;
— равномерное движение по
окружности;
— равномерное
криволинейное движение;
— криволинейное
равнопеременное движение;
— криволинейное движение
с переменным ускорением.
16

17. Кинематика.

Соответствующий угол поворота будем характеризовать вектором dφ,
модуль которого равен углу поворота, а направление совпадает с
осью вращения, причем так, что направление поворота отвечает
правилу правого винта по отношению к направлению вектора dφ.
Тогда элементарное перемещение материальной точки при таком
повороте связано с углом поворота соотношением:
dr =r sin d
или в векторном виде:
dr d ,r
.

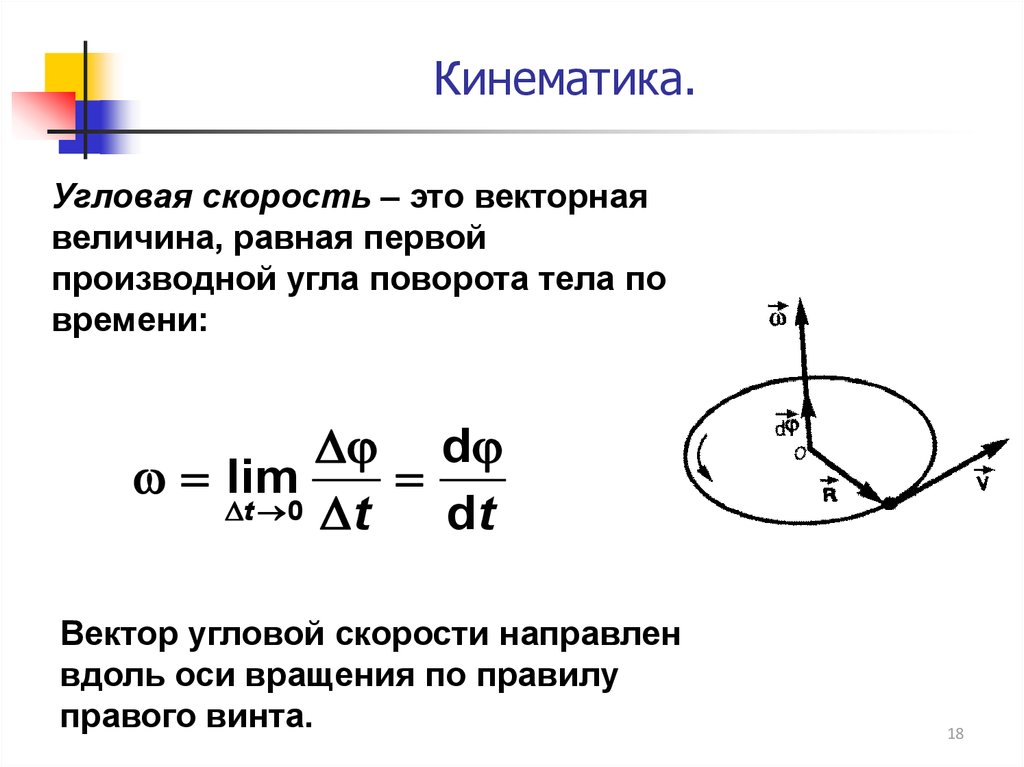
18.

Кинематика.
Угловая скорость – это векторная
величина, равная первой
производной угла поворота тела по
времени:
d
lim
t 0 t
dt
Вектор угловой скорости направлен
вдоль оси вращения по правилу
правого винта.
18

19.

Кинематика.
Линейная скорость точки:
s
R
d
v lim
lim
R
R
t 0 t
t 0 t
dt
v R
В векторном виде :
v R
Модуль векторного произведения:
R sin( R )
19

20.

Кинематика.
При равномерном вращательном движении период равен:
2
T
.
Число оборотов в единицу времени (частота ):
1
n
.
T 2
Угловая частота вращения:
2 n.
20

21.

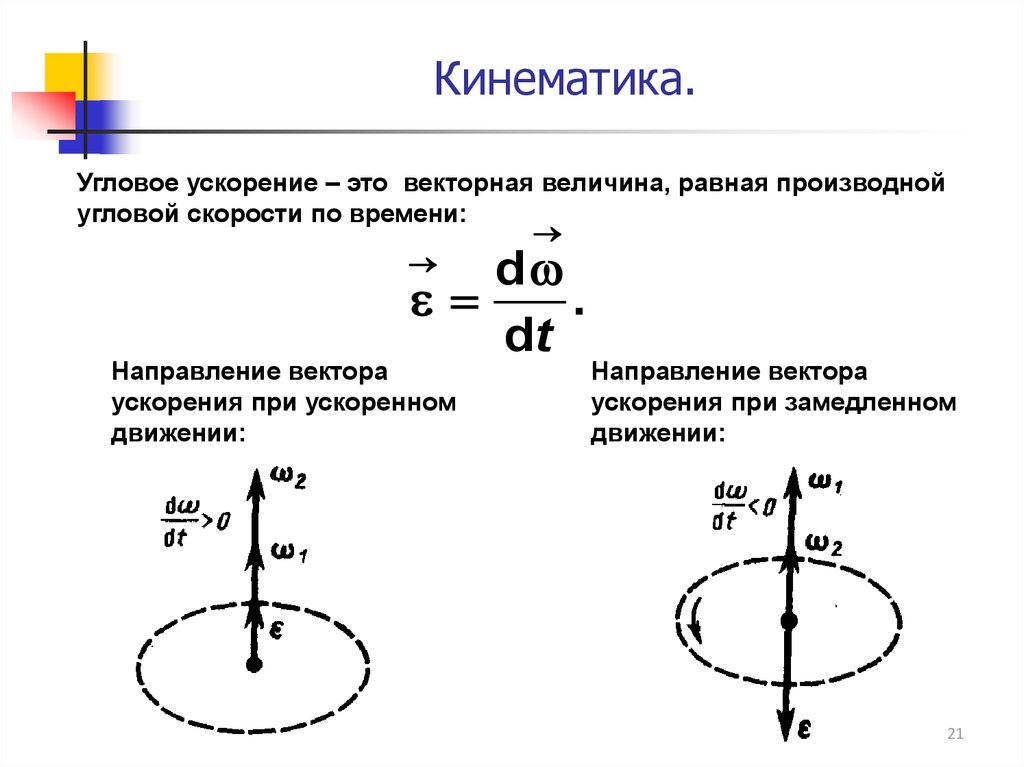
Кинематика.
Угловое ускорение – это векторная величина, равная производной
угловой скорости по времени:
d
.
dt
Направление вектора
ускорения при ускоренном
движении:
Направление вектора
ускорения при замедленном
движении:
21

22.

Кинематика.
В случае равнопеременного движения точки
по окружности ( =const):
0 t
t
0t
2
2
22

23.

Кинематика.
Тангенциальная составляющая ускорения:
dv
a
,
dt
v R ,
d R R d
a
R
dt
dt
Нормальная составляющая ускорения:
v 2 2R 2
2
an
R
R
R
23

24.

Кинематика.
Связь между линейными и угловыми величинами
выражается следующими формулами:
s R , v R , a R , an R
2
2
v
2
a a a a
R
2
2
n
2
R R
2
2
2
R
4
2
24