Similar presentations:
Кинематика. Ускорение
1.
УСКОРЕНИЕУскорение
характеризует быстроту
изменения вектора скорости со
временем.
2.
Среднее ускорение равно отношениюизменения вектора скорости к
промежутку времени, за который это
изменение произошло.
r
r Dv
a =
Dt
3.
Мгновенное ускорениеравно производной вектора скорости по
времени.
r
r
Dv
a = lim
Dt ®0 Dt
r
r dv r&
a=
=v
dt
4.
rr dr r&
Так как v =
= r , то
dt
r
r d r &
r&
a= 2 =r
dt
2
Ускорение равно второй производной
радиус-вектора по времени.
é мù
[ a] = ê с2 ú
ë û
5.
Компоненты ускоренияПредставим вектор скорости как
r
r
v = vt .
Вычислим ускорение
r
r
r d v d ( vt )
a=
=
dt
dt
r
r dv r
dt
a= t +v
dt
dt
r
r
(v t )
6.
Первое слагаемое в формулеr
r dv r
dt
a= t +v
dt
dt
дает вектор, направленный по касательной к
траектории. Его называют
касательным или тангенциальным
ускорением.
r dv r
at = t
dt
7.
По величине тангенциальное ускорениеравно производной модуля скорости по
времени
dv
at =
dt
и показывает, как быстро
величина скорости
меняется со временем.
8.
Телоразгоняется
r r
at v
r r
v at
r
r
at v
at > 0
Тело
тормозит
r
r
at v
r r
at v
r
at
r
v
r r
at v
r
r
at ¯ v
at < 0
9.
Второе слагаемое в формулеr
r dv r
dt
a= t +v
dt
dt
дает нормальную компоненту ускорения
r
r
dt
an = v
dt
10.
Проведем окружность, дуга которой совпадаетс некоторым участком траектории.
r
v r
r
t
t
dj
r
r
O
r
r =R
Точка О – центр кривизны траектории,
радиус окружности R – радиус кривизны траектории на
данном участке.
11.
rЕсли радиус-вектор r повернулся на угол dj ,
r
то и вектор t повернулся на угол dj.
Преобразуем
r
r
r
dt
dt ds dj
an = v
=v
× ×
dt
dt ds dj
r
r
ds dj dt
r
an = v × ×
×
n
dt ds dj
v 1
R
, т.к. для окружности ds = R × dj
12.
rt
dj
r
n
r
t
O
r
t
dj
r
t
dt = t × dj = 1× dj = dj
r
r
r
n
d
t
=
d
j
×
n
r
r
dt
dt r
=n
dj
13.
rn - единичный вектор
нормали к траектории движения
Направлен к центру кривизны
траектории.
r r
n ^v
14.
Нормальное ускорение2
r v r
an = n
R
По модулю
2
v
an =
R
15.
Вектор нормальногоускорения направлен к
центру кривизны
траектории и характеризует
быстроту изменения
скорости по направлению.
16.
rВектор полного ускорения a
является векторной суммой
r
тангенциального ускорения at
r
и нормального ускорения an .
r
at
r
r a
an
O
17.
r r ra = at + an
По модулю
a=
2
at
2
+ an
2
æ dv ö æ v ö
a = ç ÷ +ç ÷
è dt ø è R ø
2
2
18.
ВИДЫ ДВИЖЕНИЯ1. Равномерное движение
Равномерным называют движение с постоянной по
модулю скоростью.
По определению
При равномерном движении тангенциального ускорения нет!
Если движение криволинейное, нормальное ускорение есть.
Полное ускорение равно нормальному.
19.
2. Равномерное прямолинейное движениеВектор мгновенной скорости остается постоянным не
только по модулю, но и по направлению.
По определению
20.
3. Движение по произвольной траектории спостоянной тангенциальной составляющей вектора
ускорения aτ
По определению
21.
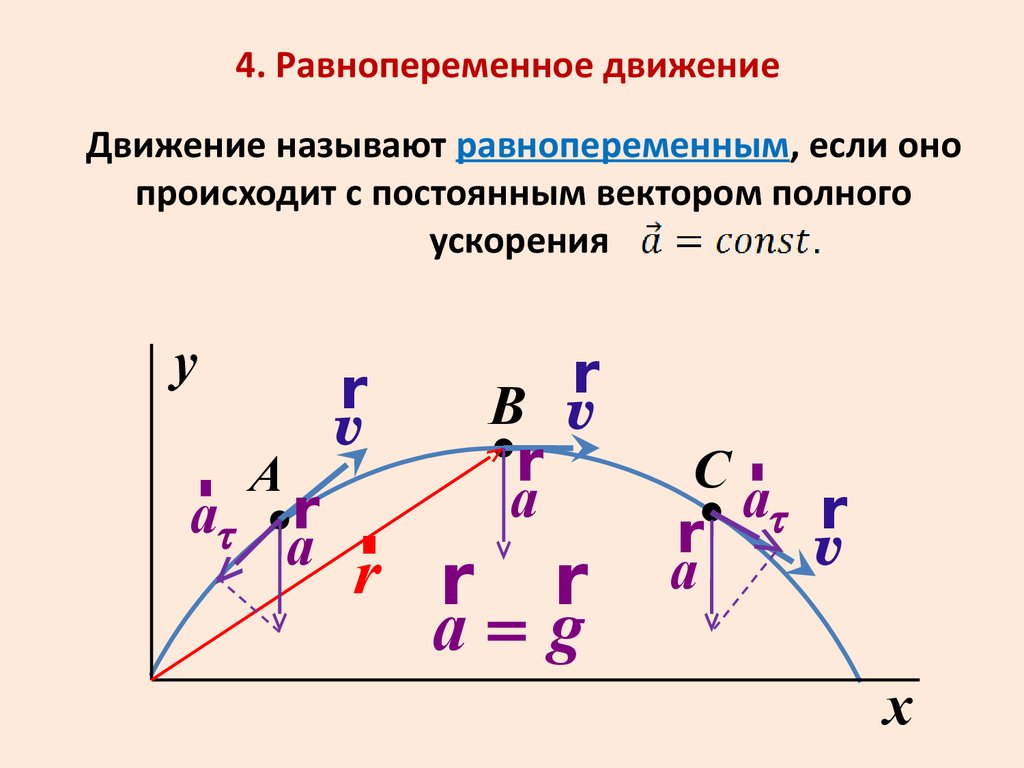
4. Равнопеременное движениеДвижение называют равнопеременным, если оно
происходит с постоянным вектором полного
ускорения
y
r
v
r A
at r r
a r
r
B v
r
a
r r
a=g
Cr
at r
r
v
a
x
22.
По определениюПо определению
23.
5. Прямолинейное равнопеременное движениеВ случае прямолинейного движения радиус кривизны
траектории R стремится к бесконечности, тогда
- движение
равноускоренное
- движение
равнозамедленное
24.
ДВИЖЕНИЕ ПО ОКРУЖНОСТИr
r
O
j
x
Движение точки по окружности задается
зависимостью φ (t).
φ – угол между радиус-вектором точки и осью х.
25.
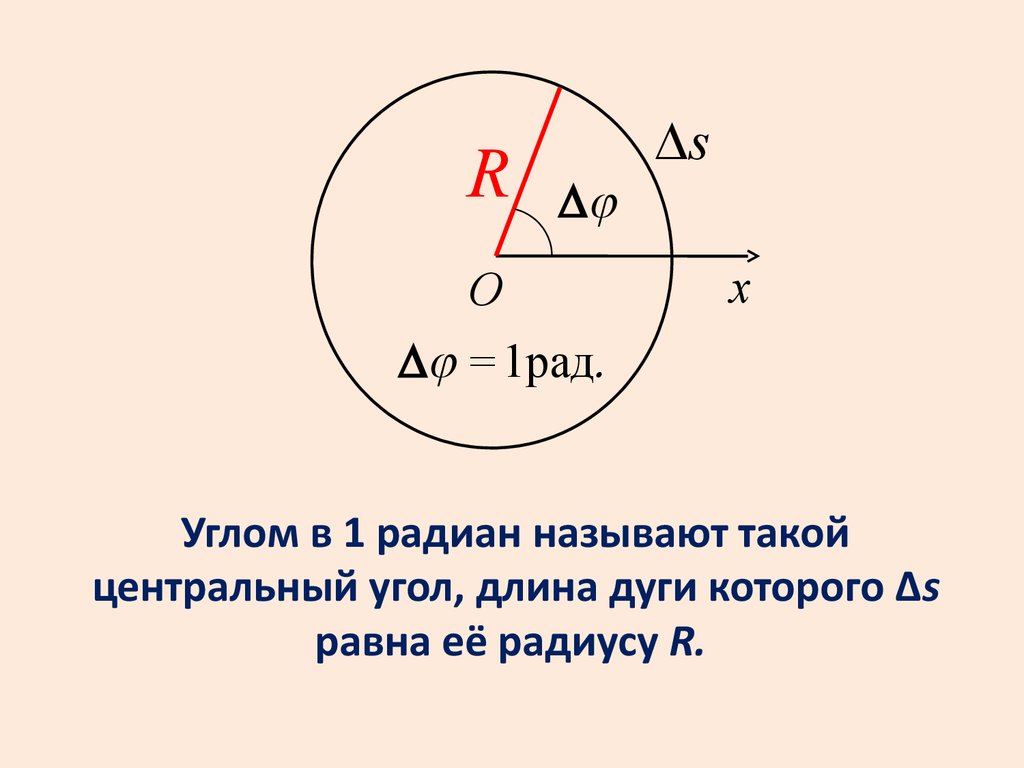
RDj
O
Dj = 1рад.
Ds
x
Углом в 1 радиан называют такой
центральный угол, длина дуги которого Δs
равна её радиусу R.
26.
Для произвольного угла поворота ΔφDs
Dj =
R
Ds = R × Dj
Угол в 1 оборот равен 2 радиан.
27.
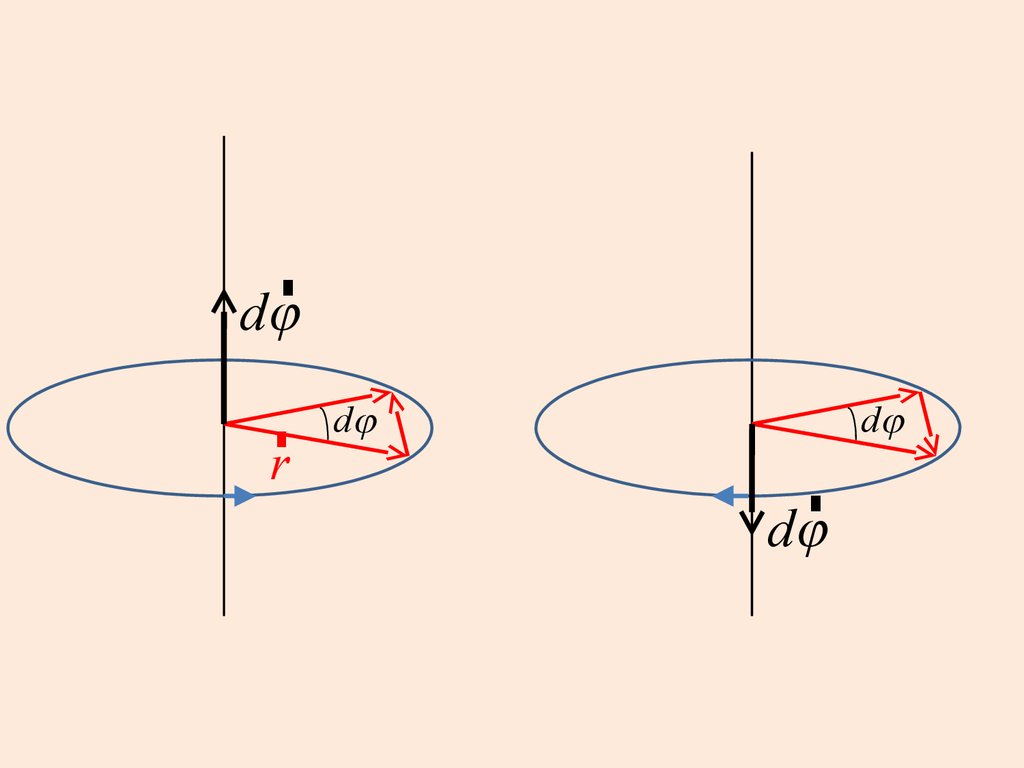
Вектор углового путиВектор углового пути по модулю равен
углу поворота.
Его направление определяется
правилом правого винта.
28.
rdj
r
r
dj
dj
r
dj
29.
Угловая скоростьУгловая скорость характеризует быстроту
движения материальной точки по окружности.
Это векторная величина равная
производной вектора углового пути по
времени.
r
r dj
é рад. ù
w=
w] = ê
[
ú
dt
ë с û
r r&
w =j
30.
Направление вектора угловой скороститакже находят по правилу правого винта.
r
w
r
w
31.
Угловое ускорениеУгловое ускорение характеризует быстроту
изменения угловой скорости со временем.
Это векторная величина равная
производной угловой скорости по времени.
r
r dw
e=
é рад. ù
dt [ e ] = êë с úû
r r&
e =w
2
32.
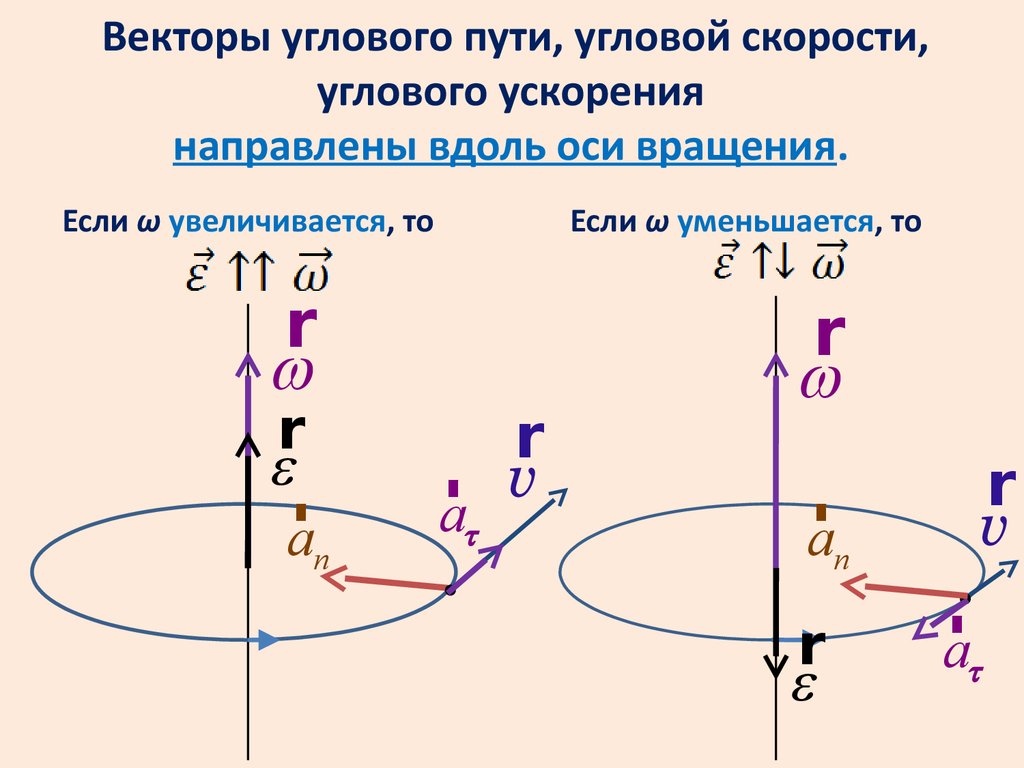
Векторы углового пути, угловой скорости,углового ускорения
направлены вдоль оси вращения.
Если ω увеличивается, то
r
w
r
e
r
an
Если ω уменьшается, то
r
r v
at
r
w
r
an
r
e
r
v
r
at
33.
Связь линейных и угловых характеристик движенияСвяжем линейный и угловой пути
ds = R × dj
Возьмем производную по времени
ds
dj
= R×
dt
dt
Получим связь линейной и угловой скоростей
v = wR
34.
Заметив, что векторы линейной иугловой скоростей, а также радиусвектор взаимно перпендикулярны и
связаны правилом правого винта,
можно записать векторное равенство:
r
r r
v = [ w ,r ]
35.
Снова возьмем производную по времени:dv
dw
=R
dt
dt
Получим
at = e R
36.
Теперь найдем нормальное ускорениеv w Rv
an = =
= wv
R
R
2
или
w R
an =
R
2
2
an = w R
2
37.
Характеристики равномерного вращенияПериод Т равен времени, за которое
происходит один оборот.
Частота вращения ν равна числу
оборотов в единицу времени.
1
1
T = иn =
n
T
Угловая скорость при равномерном вращении:
j об 2
w=
=
= 2 n
tоб
T
















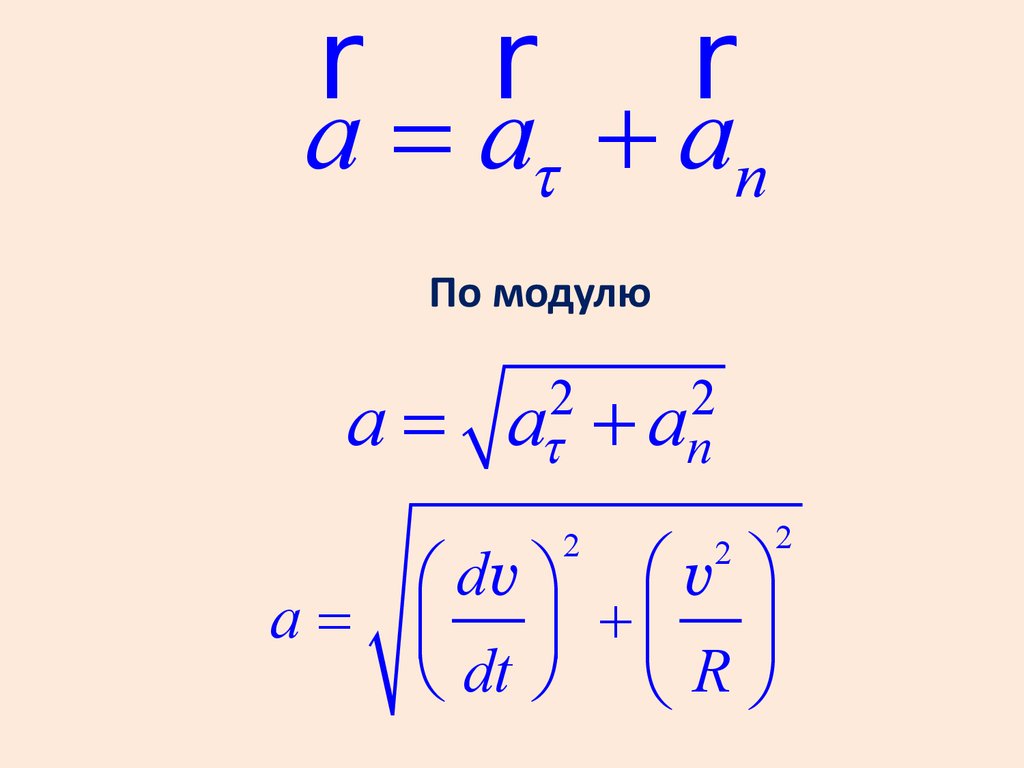
















 physics
physics








