Similar presentations:
Кинематика. Скорость точки (лекция 1)
1. Курс лекций по теоретической механике
Кинематика2. Лекция 1
КинематикаКинематика – раздел теоретической механики,
изучающий механическое движение без учета сил,
вызывающих это движение, состоит из двух отделов:
Кинематика точки
Кинематика твердого тела
Кинематика точки – изучает движение материальной точки, является базой для изучения движения точек твердого тела.
Задание движения точки – необходимо иметь возможность определения положения точки в пространстве в любой момент времени (уравнения,
геометрия механизма и известный закон движения ведущего звена).
Траектория движения точки – совокупность положений точки в пространстве при ее движении.
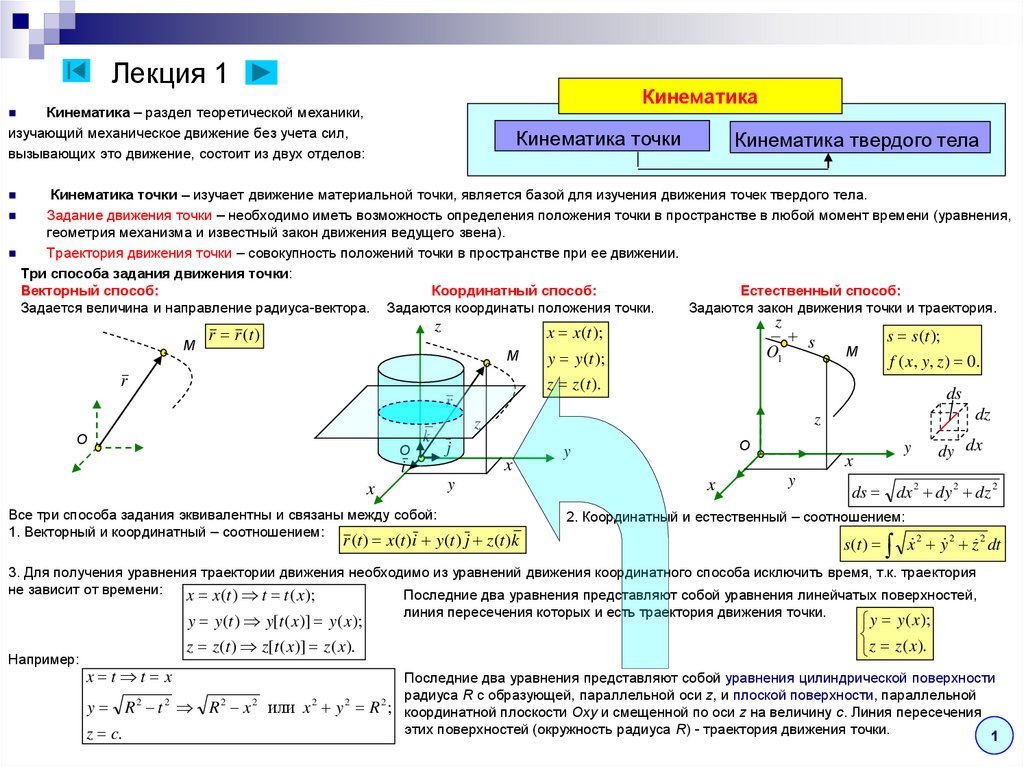
Три способа задания движения точки:
Векторный способ:
Координатный способ:
Естественный способ:
Задаются закон движения точки и траектория.
Задается величина и направление радиуса-вектора. Задаются координаты положения точки.
M
z
r r (t )
M
z
s
O1
x x (t );
y y (t );
M
s s (t );
f ( x , y , z ) 0.
z z (t ).
r
ds
r
O
O
k
j
x
i
y
x
Все три способа задания эквивалентны и связаны между собой:
1. Векторный и координатный – соотношением:
dz
z
z
O
y
x
x
y
y
dy dx
ds dx 2 dy 2 dz 2
2. Координатный и естественный – соотношением:
r (t ) x(t )i y(t ) j z (t )k
s(t ) x 2 y 2 z 2 dt
3. Для получения уравнения траектории движения необходимо из уравнений движения координатного способа исключить время, т.к. траектория
не зависит от времени:
Последние два уравнения представляют собой уравнения линейчатых поверхностей,
x x(t ) t t ( x);
Например:
y y (t ) y[t ( x)] y ( x);
z z (t ) z[t ( x)] z ( x).
x t t x
y R2 t 2 R2 x2
z c.
линия пересечения которых и есть траектория движения точки.
y y ( x);
z z ( x).
Последние два уравнения представляют собой уравнения цилиндрической поверхности
радиуса R c образующей, параллельной оси z, и плоской поверхности, параллельной
или x 2 y 2 R 2 ; координатной плоскости Oxy и смещенной по оси z на величину c. Линия пересечения
этих поверхностей (окружность радиуса R) - траектория движения точки.
1
3. Лекция 1 (продолжение – 1.2)
Скорость точки – величина, характеризующая быстроту изменения положения точки в пространстве.Три способа задания движения точки определяют способы определения скорости точки:
Векторный способ: Сравним два положения точки в моменты времени t и t1= t + t:
t
r;
t1 t Δt r1 r Δr ;
M
v
Δr
r
M1 v
ср
O
dr
dt
- вектор средней скорости в интервале времени t,
направлен по направлению вектора перемещения (хорде MM1).
Предел отношения приращения функции
Δ r dr
к приращению приращения аргумента есть Δt lim 0
Δt dt
производная функции (по определению):
- вектор истинной скорости точки в момент времени t, направлен по касательной к траектории
(при приближении M1 к M хорда занимает положение касательной).
Устремим t 0 и перейдем к пределу:
v
r1
Δr
vср
Δt
Δt
lim 0
Δr
v
Δt
r (t ) x(t )i y(t ) j z (t )k
Координатный способ: Связь радиуса-вектора с координатами определяется выражением:
z
vz
Используем векторную форму определения скорости:
M
dr (t ) d
x(t )i y (t ) j z (t )k Компоненты
vy v
Проекции
v x x ;
dt
dt
(составляющие) v x x (t )i ;
скорости
vx
вектора
r
v y y ;
v y y (t ) j; на оси
dx
dy
dz
i
j
k
v
i
v
j
v
k
скорости:
x
y
z
координат:
z
O
dt
k
j
y
x
s M
Δs
O1
r
r1
O
v x 2 y 2 z 2 ;
x
cos( v , x) ;
v
y
cos( v , y ) .
v
Используем векторную форму определения скорости:
Естественный способ:
Δr
v z z .
v z z (t )k .
dt
y
x
i
dt
Представим радиус-вектор как сложную функцию: r (t ) r [ s (t )].
dr
Δr
Представим производную
lim 0
.
радиус-вектора как предел: ds Δs
Δs
v
M1
Величина производной
радиуса-вектора
по дуговой координате равна 1:
dr (t ) dr ds dr
s .
dt
ds dt ds
Вектор приращения радиуса-вектора направлен по хорде MM1
и в пределе занимает положение касательной.
При s 0 радиус кривизны 1 , угол
2 sin Δ2
dr
Δr
Δs lim 0
Δ lim 0
1. между радиусами кривизны 0, числитель ds
Δs
Δ
- основание равнобедренного треугольника,
Таким образом, производная радиуса-вектора по дуговой координате есть
единичный вектор, направленный по касательной к траектории.
Вектор скорости равен:
v
v s . Проекция скорости на касательную: v s .
При s 0 вектор скорости направлен в сторону увеличения дуговой
координаты, В противном случае – в обратную сторону.
знаменатель – длина круговой дуги радиуса .
Δr
Δ
1
Δs
2
4. Лекция 2
Ускорение точки – величина, характеризующая быстроту изменения скорости точки.t
v;
Три способа задания движения точки определяют способы определения ускорения точки:
Векторный способ: Сравним скорости точки в двух положениях точки в моменты времени t и t1= t + t:
t1 t Δt v1 v Δv ;
M
Δv
v
v
- вектор среднего ускорения в интервале времени t, направлен в сторону вогнутости траектории.
a
Δr
r
O
v1
a
r1
Δt
M1
v
v1
a
ср
Переходя к пределу получаем:
dv d 2 r
dt dt 2
Δt lim 0
Δv
a
Δt
Δt lim 0
Δ v dv
Δt
dt
- вектор истинного ускорения точки в момент времени t, лежит в
соприкасающейся плоскости (предельное положение плоскости, проведенной
через касательную в точке M и прямую, параллельную касательной в точке M1, при
стремлении M1 к M) и направлен в сторону вогнутости траектории.
Координатный способ: Используем полученное векторное выражение и связь радиуса-вектора с координатами
z
az
M
ay
r
O
i
k
ax
z
j
x
d 2 r (t ) d 2
a
2 x(t )i y (t ) j z (t )k
dt 2
dt
2
2
d x
d y
d 2z
2 i 2 j 2 k axi a y j az k
dt
dt
dt
Компоненты
(составляющие)
вектора
ускорения:
y
a x x i ;
a y y j;
a z z k .
Проекции
ускорения
на оси
координат:
r (t ) x(t )i y(t ) j z (t )k
a x 2 y 2 z 2 ;
a x x ;
x
a y y ; cos( a , x) ;
a
a z z .
y
cos( a , y ) .
a
y
Таким образом полное ускорение точки есть векторная сумма двух ускорений:
Естественный способ: Используем векторное выражение для ускорения и выражение для скорости при естественной способе задания: v s .
касательного, направленного по касательной к траектории в сторону увеличения
дуговой координаты,
если s 0 (в противном
случаеединичного
– в противоположную)
d d dsи
d
dv d
d
Представим
единичный
Производная
s M
s .
a
( s ) s s
. касательный
(
t
)
[
s
(
t
)].
нормального
ускорения,
направленного
по
нормали
к
касательной
в сторону
центра
вектор
касательного
вектора:
Δs
dt dt
dt
O1
dt
ds dt
ds
кривизны
(вогнутости
avτ
как
сложную
функцию: траектории): a a a .
τ
n
n
Величина производной
Таким образом, производная
M1
a n Δr
единичного касательного вектора d
2 sin Δ2 2 1 2единичного касательного вектора
Δ
Модуль
r
Δs полного
lim 0 ускорения:
Δ lim 0 a a τ . a n по; дуговой координате есть вектор,
по дуговой координате:
a
ds
Δs
Δ
направленный перпендикулярно
r1
Приединичный
s 0 радиус
кривизны
1 , угол
Угол между приращением касательной к траектории.
Введем
вектор
n, нормальный
(перпендикулярный)
к касательной,
O
a s ;
1
между радиусами
единичного вектора
направленный
к центрукривизны
кривизны. 0, числитель Компоненты
Δs
a τ s ;
Δr
Проекции
2
-основание
равнобедренного
треугольника,
и
самим
вектором
2
С использованием вектора n и ранее
s (составляющие)
s
о
2
образованного
единичными векторами 1 и a
, s Δ
при 0, стремится
n . вектора
определенных
величин
a n кn90
. . ускорения a s .
3
знаменатель
–
длина
круговой
дуги
радиуса
.
на
оси
и
n:
1
ускорение представляется как сумма векторов:
n
ускорения:
x
1
5. Лекция 2 (продолжение 2.2)
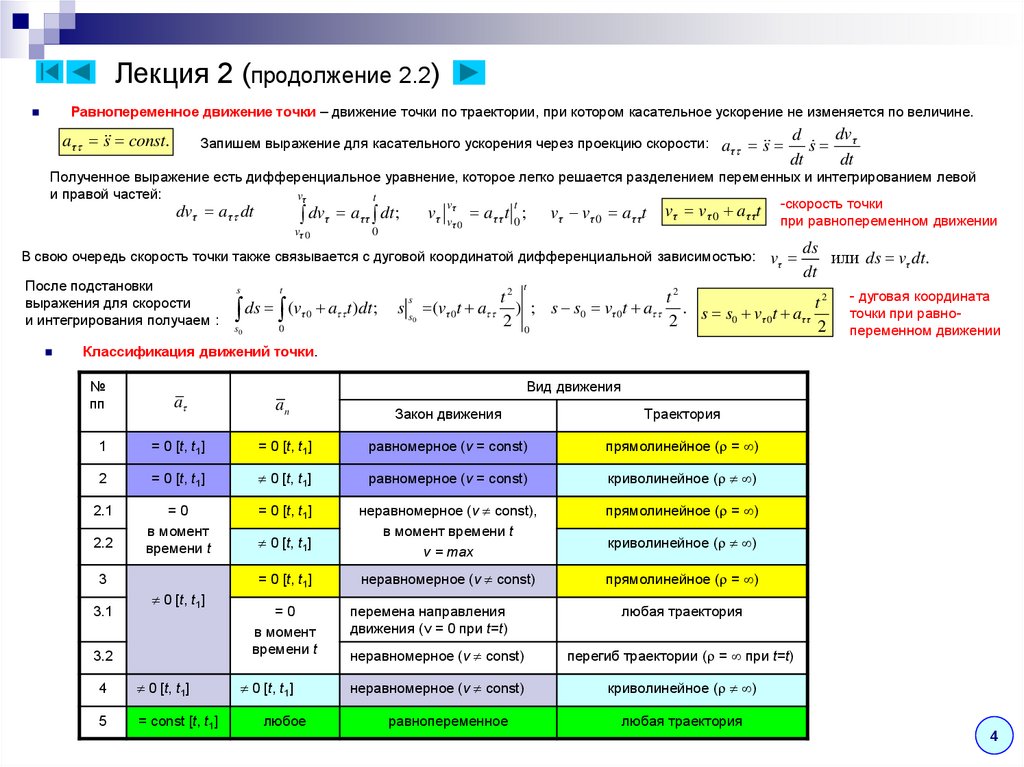
Равнопеременное движение точки – движение точки по траектории, при котором касательное ускорение не изменяется по величине.a τ s const.
Запишем выражение для касательного ускорения через проекцию скорости:
a τ s
dv
d
s τ
dt
dt
Полученное выражение есть дифференциальное уравнение, которое легко решается разделением переменных и интегрированием левой
и правой частей:
vτ
t
v
t
-скорость точки
dv τ a τ dt
dv
a
v τ vτ a τ τ t 0 ; v τ v τ 0 a τ τt v τ v τ 0 a τ τt при равнопеременном движении
τ
τ τ dt ;
τ0
vτ 0
0
В свою очередь скорость точки также связывается с дуговой координатой дифференциальной зависимостью: vτ
После подстановки
выражения для скорости
и интегрирования получаем :
s
t
t
ds (v a t )dt;
τ0
s0
0
ds
или ds vτ dt.
dt
2
t2
t2
s s (vτ 0t a ) ; s s0 vτ 0t a . s s v t a t
0
0
τ0
ττ
2 0
2
2
s
- дуговая координата
точки при равнопеременном движении
Классификация движений точки.
№
пп
a
an
Закон движения
Траектория
1
= 0 [t, t1]
= 0 [t, t1]
равномерное (v = const)
прямолинейное ( = )
2
= 0 [t, t1]
0 [t, t1]
равномерное (v = const)
криволинейное ( )
2.1
=0
в момент
времени t
= 0 [t, t1]
прямолинейное ( = )
0 [t, t1]
неравномерное (v const),
в момент времени t
v = max
= 0 [t, t1]
неравномерное (v const)
прямолинейное ( = )
2.2
Вид движения
3
3.1
0 [t, t1]
3.2
4
0 [t, t1]
5
= const [t, t1]
=0
в момент
времени t
0 [t, t1]
любое
криволинейное ( )
перемена направления
движения (v = 0 при t=t)
любая траектория
неравномерное (v const)
перегиб траектории ( = при t=t)
неравномерное (v const)
криволинейное ( )
равнопеременное
любая траектория
4
6. Лекция 2 (продолжение 2.3)
Исследование работы кривошипно-шатунного механизма – См. решение задачи М.12.18 “Теоретическая механика в примерах изадачах. Кинематика” (электронное пособие автора www.miit.ru/institut/ipss/faculties/trm/main.htm ),
Кинематика твердого тела – изучает движение твердого тела, кинематика точки используется для получения новых зависимостей и
формул.
Существует пять видов движения твердого тела:
1. Поступательное (ползун, поршень насоса, спарник колес паровоза, движущегося по прямолинейному пути, кабина лифта, дверь купе,
кабина колеса обозрения).
2. Вращательное (маховик, кривошип, коромысло, колесо обозрения, обычная дверь).
3. Плоскопараллельное или плоское (шатун, колесо локомотива при качении по прямолинейному рельсу, шлифовальный круг).
4. Сферическое (гироскоп, шаровая стойка).
5. Общий случай движения или свободный полет (пуля, камень, небесное тело)
Поступательное движение твердого тела – такое движение при котором любая прямая, жестко связанная с телом, остается
параллельной самой себе. Обычно поступательное движение отождествляется с прямолинейным движением его точек, однако это не
так. Точки и само тело (центр масс тела) могут двигаться по криволинейным траекториям, см. например, движение кабины колеса
обозрения.
Теорема о поступательном движении твердого тела – При поступательном движении твердого тела все его точки описывают
тождественные траектории и имеют в каждый момент времени геометрически равные скорости и ускорения.
Проведем радиус-векторы к двум точкам A и B, а также соединим эти точки вектором rBA.
В любой момент времени выполняется векторное равенство:
В любой момент времени вектор rBA остается постоянным по направлению
(по определению поступательного движения) и по величине
rA (t ) rB (t ) const ,
(расстояние между точками не изменяется).
Отсюда:
и это означает, что в каждый момент времени положение точки A отличается от положения
Таким
твердого
тела полностью
точкиобразом,
B на однупоступательное
и ту же величинудвижение
rBA = const,
т.е. траектории
этих двух определяется
точек тождественны
движением
одной
точки,
принадлежащей
этому
телу
и
выбранной
произвольным образом.
(совпадают друг с другом при наложении).
Все параметры движения этой точки (траектория, скорость и ускорение) описываются
drA (t ) drB (t )
уравнениями
и соотношениями
кинематики
точки.часть соотношения:
Продифференцируем
по времени
левую и правую
vA
A
aA
rA
rA
rBA
rBA
vB
dt
B
rB
rB
C
rA (t ) rB (t ) rBA.
aB
dt
и это означает, что в каждый момент времени скорость точки A равна геометрически
(т.е. векторно) скорости точки B.
v (t ) v (t ).
A
B
Второе дифференцирование по времени приводит к соотношению:
dr 2 A (t ) dr 2 B (t )
dt 2
dt 2
и это означает, что в каждый момент времени ускорение точки A равно геометрически
(т.е. векторно) ускорению точки B.
aA (t ) aB (t ).
5
7. Лекция 3
Вращательное движение твердого тела – движение при котором все его точки движутся в плоскостях, перпендикулярных некоторойнеподвижной прямой, и описывают окружности с центрами, лежащими на этой прямой, называемой осью вращения.
P
Задание вращательное движения – движение задается законом изменения двугранного угла
φ (угла поворота), образованного неподвижной плоскостью P, проходящей через ось
вращения, и плоскостью Q, жестко связанной с телом:
(t ) - уравнение вращательного движения
Угловая скорость – величина, характеризующая быстроту изменения угла поворота.
ω
ε
t
;
t1 t Δt 1 Δ ;
Q
Δ
ср - средняя угловая скорость в интервале времени t,
Δt
Устремим t 0 и перейдем к пределу:
Δt lim 0
Δ
d
Δt
dt
Если dφ/dt > 0, то вращение происходит в сторону увеличения угла поворота,
если dφ/dt < 0, то вращение происходит в сторону уменьшения угла поворота.
Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости.
t
;
t1 t Δt 1 Δ ;
Δ
ср - среднее угловое ускорение в интервале времени t,
Δt
d
Δ
- истинное угловое ускорение
Устремим t 0 и перейдем к пределу: Δt lim 0
в момент времени t
dt
Δt
- истинная угловая скорость
в момент времени t
Угловая скорость
изображается дуговой
стрелкой в сторону
вращения.
Угловое ускорение
изображается дуговой
стрелкой в сторону
увеличения угла поворота
при
0 .
Если d2φ/dt2 и dφ/dt одного знака, то скорость увеличивается по модулю и вращение называется ускоренным (дуговые стрелки угловой скорости
и углового ускорения направлены в одну сторону),
если d2φ/dt2 и dφ/dt разного знака, то скорость уменьшается по модулю и вращение называется замедленным (дуговые стрелки угловой скорости
и углового ускорения направлены в противоположные стороны).
const.
Равномерное вращение – угловая скорость не изменяется по величине.
Равнопеременное вращение – угловое ускорение не изменяется по величине.
const.
d
;
dt
t
0
0
d dt;
0 t.
d
;
dt
d
;
dt
t
0
0
t
0
0
d dt;
d ( 0 t )dt;
0 t.
0 0t
t2
.
2
6
8. Лекция 3 (продолжение 3.2)
Скорость точки при вращательном движении твердого тела – траектория точки известна (окружность радиуса R – расстояние точкидо оси вращения), можно применить формулу для определения скорости точки при естественном задании движения:
v s .
Дуговая координата связана
с радиусом окружности:
- O
+
s
R
φ
ε
aanос
aaврτ
ω
a
v
s R.
Тогда проекция скорости
на касательную к окружности:
vτ
d
d
( R )
R R.
dt
dt
Поскольку далее работают с модулем угловой скорости после изображения ее
в виде дуговой стрелки расчетной формулой является выражение для модуля скорости: v R
и вектор скорости направляют перпендикулярно радиусу
в сторону дуговой стрелки угловой скорости.
Как следует из формулы скорость точки пропорциональна расстоянию ее до оси вращения (радиусу вращения).
Ускорение точки при вращательном движении твердого тела – траектория точки известна, можно применить
формулы для определения ускорений точки при естественном задании движения:
s 2
Тогда проекции ускорения
d2
d 2
на касательную
a
(
R
)
R R.
τ
2
2
к окружности и нормаль:
dt
dt
a τ s ; a n
1 d
1 d
(
R
)
R 2 R.
dt
R dt
2
an
2
.
Поскольку далее работают с модулем углового ускорения после изображения его в виде дуговой стрелки расчетной формулой является
выражение для касательного ускорения: a R и вектор этого ускорения, называемого вращательным ускорением, направляют
вр
перпендикулярно радиусу в сторону дуговой стрелки углового ускорения.
z
z
Нормальное ускорение теперь называется осестремительным ускорением aос R , его направляют по радиусу
к оси вращения
независимо от направления дуговой стрелки угловой скорости, не говоря уж о направлении дуговой стрелки углового ускорения.
2
ω
Как следует из формул оба ускорения точки пропорциональны расстоянию ее до оси вращения (радиусу вращения).
ω
Угол между направлением полного ускорения и
радиусом от величины радиуса не зависит
ε и
ε
равен:
aвр
Скорость и ускорения точки при вращательном движении как векторные произведения.
arctg arctg 2 .
Представим угловую скорость и угловое ускорения как векторы, направленные по оси вращения в ту
aос
сторону, откуда дуговые стрелки этих величин указывают вращение против часовой стрелки.
Полное ускорение точки, как и ранее, есть векторная сумма этих ускорений: a a
вр a ос .
Положительное направление оси z можно задать с помощью единичного вектора k, тогда
векторы угловой скорости и углового ускорения можно представить как:
z k z k
где z, z – проекции соответствующих векторов на ось z.
k
k
7
9. Лекция 3 (продолжение 3.3)
Скорость точки при вращательном движении как векторное произведение – определяется выражением v r , котороеописывает и величину, и направление скорости.
Величина (модуль) этого
Таким образом: v R.
v 1 r sin( , r ).
векторного произведения:
ω
2 произведения:
Направление вектора рассматриваемого векторного
по определению векторного произведения – перпендикулярноRплоскости, проведенной через умножаемые вектора,
направлен в ту сторону, откуда поворот первого вектора ко второму на наименьший угол кажется происходящим
против часовой стрелки;
по правилу правой руки – при совмещении большого пальца с первым вектором, остальных – со вторым вектором,
поворот большого пальца перпендикулярно ладони указывает на направление вектора векторного произведения.
R
r
v
Таким образом, действительно векторное произведение угловой скорости и радиус-вектора полностью определяет
величину и направление скорости точки при вращательном движении в соответствии с ранее полученными результатами.
Вращательное ускорение точки как векторное произведение – определяется выражением
описывает и величину, и направление вращательного ускорения.
ε
R
r
a вр r
, которое
Таким образом:
Величина (модуль) этого векторного a
aвр R.
вр r sin( , r ).
произведения:
Направление вектора рассматриваемого векторного произведения можно установить по определению векторного
произведения или по правилу правой руки.
R
образом, действительно векторное произведение углового ускорения и радиус-вектора полностью определяет
a вр Таким
величину и направление вращательного ускорения точки в соответствии с ранее полученными результатами.
Осестремительное ускорение точки как векторное произведение – определяется
выражением a v , которое описывает и величину, и направление осестремительного
ос
ускорения.
Величина (модуль) этого
векторного произведения:
aос v sin( , v ). Таким образом: v v ( R) 2 R.
Направление вектора рассматриваемого векторного произведения можно установить по определению векторного
произведения или по правилу правой руки.
1, т.к. вектор скорости точки перпендикулярен плоскости,
Таким образом, действительно векторное произведение угловой
скорости
и вектора
скорости
точки полностью
в которой
лежит
вектор угловой
скорости.
определяет величину и направление осестремительного ускорения точки в соответствии с ранее полученными
результатами.
Это векторное произведение может быть также записано в виде: a ( r )
ос
ω
R
r
a ос
v
8
10. Лекция 3 (продолжение 3.4)
Формулы Эйлера – с помощью раскрытия векторного произведения для скорости точки можно получить общие аналитическиевыражения для этой скорости через координаты рассматриваемой точки при произвольной расположении оси вращения в
пространстве:
i
v r x
x
z
ω
R
j
k
y z ( y z z y )i ( z x x z ) j ( x y y x)k
y
z
v x y z z y;
v y z x x z;
Отсюда получаются аналитические формулы для проекций скоростей точки:
r
z
x
y
x
y
v z x y y x.
v
Преобразования вращательных движений – изменение величины и направление угловых
скоростей вращающихся звеньев в различных передаточных механизмах:
Фрикционное зацепление:
v2 v1
Скорости входящих в контакт точек колес при отсутствии проскальзывания равны:
v1 v2 ;
1 R1 2 R2 . Отсюда:
1 R2
2 R1
ω2
R2
Передаточное число, характеризующее изменение скорости вращения при передаче
вращения от одного звена к другому – отношение угловой скорости ведущего колеса
R
i1 2 1 2
к угловой скорости ведомого:
2 R1
Зубчатое зацепление – число зубьев каждого из колес прямо пропорционально
радиусу колеса. Окружные скорости входящих в контакт точек поверхностей зубьев по-прежнему равны.
Полученные соотношения остаются справедливыми, в том числе и для случая внутреннего
зацепления.
Радиусы делительных окружностей связаны с шагом зубьев соотношениями: 2 R z h 2 R z h
2
2
1
1
С использованием чисел зубьев каждого из колес имеем:
Ременная и цепная передачи –. Окружные скорости
входящих в контакт с ремнем или цепью точек поверхностей
обоих колес или зубьев этих колес по-прежнему равны (ремень
или цепь не растягиваются и не сжимаются).
1
Полученные соотношения остаются справедливыми.
2
1 z 2
2 z1
v2
R2
R1
1 z 2
2 z1
R1
ω2
R2
ω1
R1
v1
ω2
ω1
ω1
R2
R1
9
11. Лекция 4
Плоскопараллельное движение твердого тела – движение при котором каждая точка тела движется в в плоскостипараллельной некоторой неподвижной плоскости. Сечение тела одной из таких плоскостей есть плоская фигура, остающаяся в этой
плоскости при движении тела.
Теорема о плоскопараллельном движении твердого тела – плоскопаралллельное
движение твердого тела однозначным образом определяется движением плоской
фигуры, образованной сечением тела одной из параллельных плоскостей.
M1
Выберем две точки на произвольных двух сечениях тела, находящиеся на одном перпендикуляре к
этим плоскостям:
Проведем к каждой точке радиусы-векторы из неподвижной точки O и свяжем их между собой вектором
r1 M 1 M 2
M1M2:
r2 r1 M 1 M 2
M2
O
r2
При плоском движении тела вектор M1M2 не изменяется по величине, остается параллельным
самому себе (движется поступательно) и, следовательно, точки этого вектора описывают
тождественные траектории и имеют в каждый момент времени одинаковые скорости и ускорения:
dr2 dr1
d 2 r2 d 2 r1
; (M 1M 2 const ); v2 v1 , и
2 ; a2 a1 .
dt
dt
dt 2
dt
Таким образом, при плоском движении тела движение каждой точки одной из плоских фигур определяет движение соответствующих точек,
находящихся во всех других смежных параллельных плоскостях.
Следствие: Поскольку положение плоской фигуры однозначно определяется положением ее двух точек или отрезка прямой, проведенной
через эти точки, то плоскопараллельное движение твердого тела определяется движением прямолинейного отрезка,
принадлежащего одному из сечений тела параллельными плоскостями.
Разложение плоскопараллельного движения плоской фигуры на поступательное и вращательное движения – Плоскую фигуру
или отрезок прямой можно перевести из одного положения в другое бесчисленным множеством способов, меняя последовательность
выполнения поступательного и вращательного движения между собой, а также выбирая различные траектории и точки в качестве
полюса:
Таким образом, плоскопараллельное движение состоит из двух движений:
поступательное и вращательное, и его всегда можно разложить на эти два движения.
A1 y
При этом поступательное зависит от выбора полюса и траектории движения, а
Уравнение движения плоской фигуры: Выбирая в качестве полюса любую точку, например,
вращательное, характеризуемое поворотом вокруг выбранного полюса, не зависит от выбора
B
A, поступательная часть движения будет описываться уравнениями движения этой точки.
полюса (для любого полюса величина угла поворота и направление вращения – одинаковы).
Вращательная часть движения описывается уравнением изменения угла поворота вокруг
B
xC
A2
полюса:
Уравнения движения любой точки плоской фигуры, положение
yC
x A x A (t );
B2
A
xA
которой задается координатами локальной системы отсчета,
связанной с фигурой:
y
y
(
t
);
A
A
A
xC x A (t ) xC cos (t ) yC sin (t );
yA
(
t
).
x
10
yC y A (t ) xC sin (t ) yC cos (t ).
B1
12. Лекция 4 (продолжение 4.2)
Независимость угловой скорости и углового ускорения плоской фигуры от выбора полюса – Выберем два произвольныхпрямолинейных отрезка, изображающих положение плоской фигуры и два полюса на этих отрезках:
D
A
A
Углы наклона отрезков к горизонтальной оси различны и связаны между собой соотношением:
С
A B
Продифференцируем это соотношение:
После повторного дифференцирования следует,
d CA d DB
.
что угловые ускорения двух отрезков также равны:
dt
dt
CA DB .
Теорема о сложении скоростей – Скорость любой точки плоской фигуры равна геометрической
сумме скоростей полюса и вращательной скорости этой точки вокруг полюса.
rB (t ) rA (t ) rAB (t ).
vBA
Продифференцируем это соотношение:
Второе слагаемое есть вращательная
скорость точки B вокруг полюса A:
B
rB
rA
rAB
vvAA
vBA (t ) (t ) rAB (t );
vC
vBA b vB
vA
C
vA
zk
z
rAB const.
v A (t )
vBA (t )
z k
k
Таким образом, скорость точки B
равна геометрической сумме
скорости полюса A и
вращательной скорости точки B
вокруг полюса :
vB vA rAB vA vBA.
Следствие 1 – Проекции скоростей точек плоской фигуры на ось,
проходящую через эти точки равны .
( x1 ) : vBx1 v Ax1 , (vBA x1 ).
Спроецируем векторное соотношение на ось x1:
vCA c
B
drB (t ) drA (t ) drAB (t )
.
dt
dt
dt
vB (t )
A
O
Таким образом, угловая
скорость и угловое ускорение
плоской фигуры не зависят
от выбора полюса и их
можно представить в виде
векторов, перпендикулярных
плоскости фигуры:
Радиусы-векторы точек A и B связаны между собой соотношением:
x1
vB
A
CA DB .
Отсюда следует, что угловые скорости двух отрезков равны:
B
B
d B (t ) d A (t )
, (α const ).
dt
dt
B (t ) A (t ) .
vA
Следствие 2 – Концы векторов скоростей точек плоской фигуры, лежащих на одной прямой, также
лежат на одной прямой и делят эту прямую на отрезки пропорциональные расстояниям между точками.
Концы векторов вращательных скоростей точек B и A лежат на одной прямой и делят ее на отрезки
пропорциональные расстояниям между точками:
vCA AC Ac
vBA AB, vCA AC ,
.
Концы векторов скоростей полюса A лежат, изображенных
vBA AB Ab
в точках B и C также лежат на одной прямой.
Нетрудно доказать из подобия треугольников, что концы векторов скоростей точек B и C также лежат на одной
прямой, и делят эту прямую на части, пропорциональные расстояниям между точками.
11
13. Лекция 4 (продолжение 4.3)
Мгновенный центр скоростей (МЦС) – При движении плоской фигуры в каждый момент времени существует точка, жесткосвязанная с плоской фигурой, скорость которой в этот момент равна нулю.
Пусть известна скорость одной из точек фигуры и угловая скорость вокруг этой точки:
vPA
Запишем векторное соотношение для скорости некоторой точки P согласно теоремы о сложении скоростей:
vP vA rAP vA vPA. Зададим значение скорости этой точки P равной нулю: vP 0.
P
vA
A
vA
Тогда получаем:
vPA rAP vA . Т.е. вращательная скорость искомой точки должна быть равна по
модулю скорости точки A, параллельна этой скорости и направлена
в противоположную сторону.
Это позволяет найти положение МЦС (точки P), а именно: МЦС должен находиться на перпендикуляре к
скорости точки A, отложенном в сторону угловой скорости, на расстоянии:
AP
vA
.
Если положение МЦС найдено, скорость любой точки плоской фигуры может быть легко определена посредством выбора полюса в
МСЦ . В этом случае векторное выражение теоремы о сложении скоростей вырождается в известную зависимость скорости от
расстояния до центра вращения:
v B v P rPB v BP ;
(v P 0);
v B BP ;
vC v P rPC vCP ;
(v P 0);
vC CP;
Другими словами, можно утверждать, что в любой момент времени тело
не совершает никакого другого движения,
кроме как вращательного движения вокруг МЦС.
P
B
vB
C
vC
12











 physics
physics








