Теоретическая механика. Кинематика. Лекция 3

1.

ТЕОРЕТИЧЕСКА
Я МЕХАНИКА
КИНЕМАТИКА

2. Лекция 3

Вращательное движение твердого
тела – движение при котором все его
точки движутся в плоскостях,
перпендикулярных некоторой
неподвижной прямой, и описывают
окружности с центрами, лежащими на
этой прямой, называемой осью
вращения.

3.

P
Q
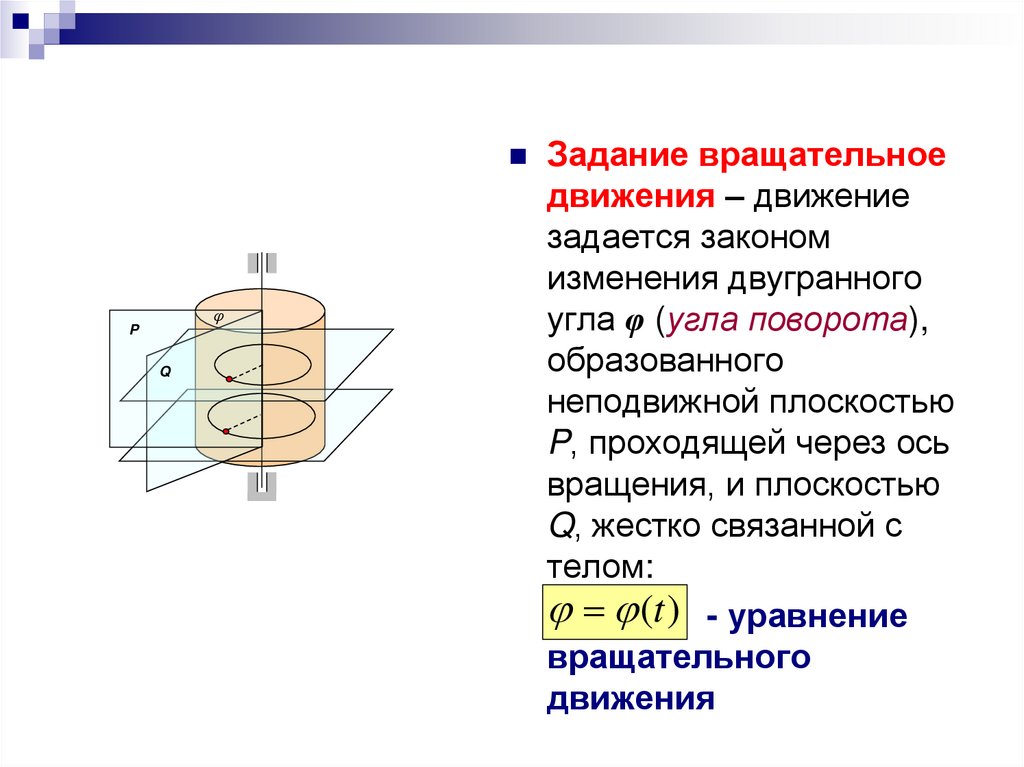
Задание вращательное
движения – движение
задается законом
изменения двугранного
угла φ (угла поворота),
образованного
неподвижной плоскостью
P, проходящей через ось
вращения, и плоскостью
Q, жестко связанной с
телом:
(t ) - уравнение
вращательного
движения

4.

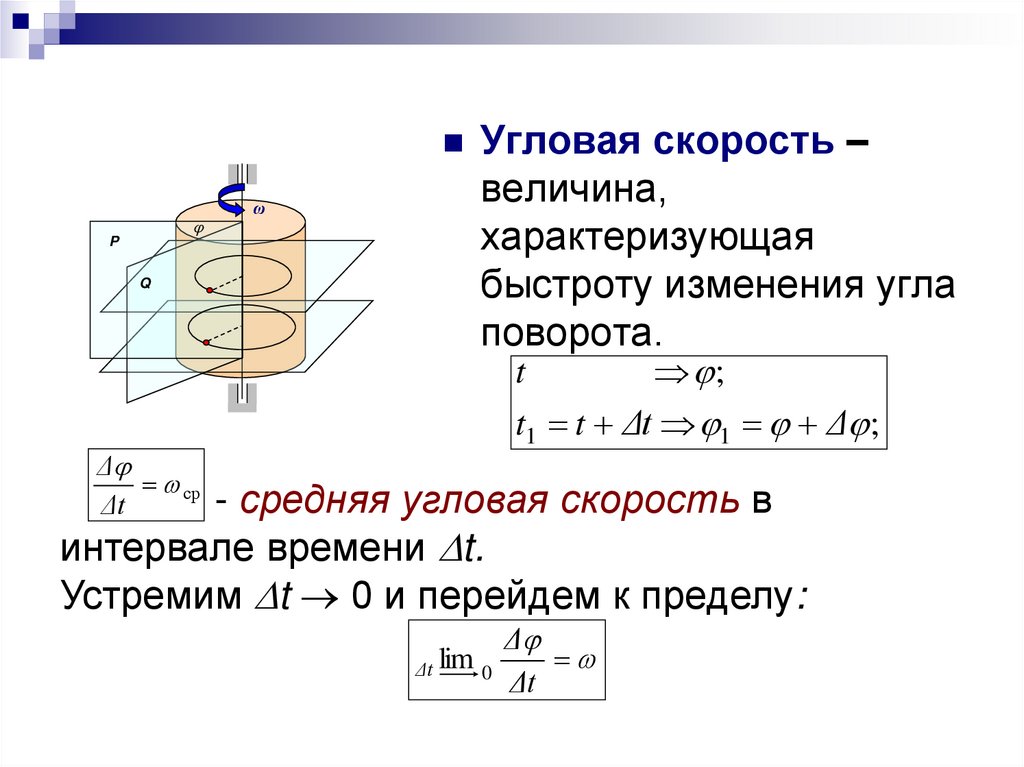
Угловая скорость –
P
Q
ω
величина,
характеризующая
быстроту изменения угла
поворота.
t
;
t1 t Δt 1 Δ ;
Δ
ср
- средняя угловая скорость в
Δt
интервале времени t.
Устремим t 0 и перейдем к пределу:
Δt lim 0
Δ
Δt

5.

P
Q
ω
d
dt
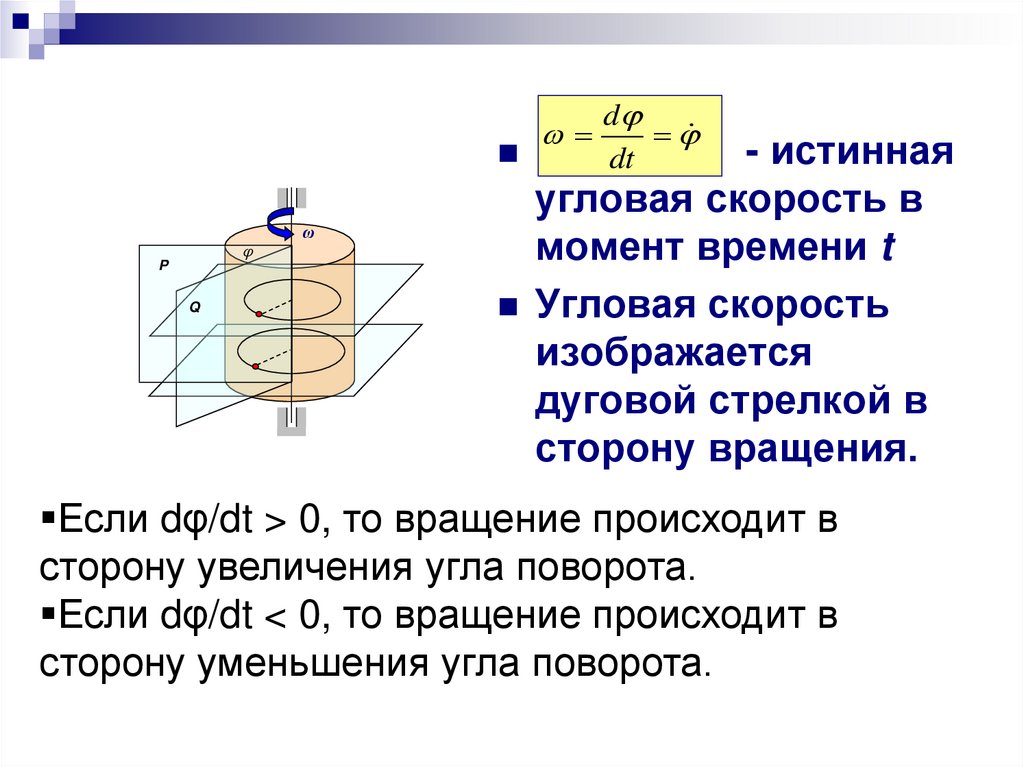
- истинная
угловая скорость в
момент времени t
Угловая скорость
изображается
дуговой стрелкой в
сторону вращения.
Если dφ/dt > 0, то вращение происходит в
сторону увеличения угла поворота.
Если dφ/dt < 0, то вращение происходит в
сторону уменьшения угла поворота.

6.

Угловое ускорение –
P
ω
ε
Q
величина,
характеризующая
быстроту изменения
угловой скорости.
t
;
t1 t Δt 1 Δ ;
Δ
ср
Δt
- среднее угловое ускорение в
интервале времени t
Устремим t 0 и перейдем к пределу:
Δt lim 0
Δ
Δt

7.

P
ω
ε
Q
d
dt
- истинное
угловое ускорение в
момент времени t.
Угловое ускорение
изображается дуговой
стрелкой в сторону
увеличения угла
поворота при 0
.

8.

Если d2φ/dt2 и dφ/dt
одного знака, то скорость
увеличивается по модулю и вращение
называется ускоренным (дуговые стрелки
угловой скорости и углового ускорения
направлены в одну сторону),
Если d2φ/dt2 и dφ/dt разного знака, то
скорость уменьшается по модулю и
вращение называется замедленным (дуговые
стрелки угловой скорости и углового
ускорения направлены в противоположные
стороны).

9.

Равномерное вращение – угловая скорость
не изменяется по величине.
const.
d
;
dt
t
0
0
d dt;
0 t.
Равнопеременное вращение – угловое
ускорение не изменяется по величине.
const.
d
;
dt
d
;
dt
t
0
0
t
0
0
d dt;
d ( 0 t )dt;
0 t.
t2
0 0t .
2

10.

- O
+
s
R
φ
Скорость точки при вращательном
движении твердого тела –
траектория точки известна
(окружность радиуса R – расстояние
точки до оси вращения), можно
применить формулу для определения
скорости точки при естественном
задании движения:
v s .
Дуговая координата связана с радиусом
окружности:
s R.

11.

- O
+
s
R
φ
ω
Тогда проекция скорости на
касательную к окружности:
d
d
v τ ( R )
R R.
dt
dt
v
Поскольку далее работают с модулем угловой
скорости после изображения ее в виде дуговой
стрелки расчетной формулой является выражение
для модуля скорости:
Вектор скорости направляют перпендикулярно
радиусу в сторону дуговой стрелки угловой скорости.
Как следует из формулы скорость точки
пропорциональна расстоянию ее до оси
вращения (радиусу вращения).

12.

Ускорение точки при
- O
+
s
R
φ
ω
an
aτ
v
вращательном движении
твердого тела – траектория
точки известна, можно
применить формулы для
определения ускорений точки
при естественном задании
движения:
aτ s ; an
s 2
.

13.

- O
+
s
R
φ
a врa τ
ε
ω
an
Тогда проекции ускорения на
касательную к окружности и
нормаль: 2
2
d
d
a τ 2 ( R) 2 R R.
dt
dt
1 d
1 d
a n ( R )
R 2 R.
dt
R dt
2
v
2
Поскольку далее работают с модулем углового
ускорения после изображения его в виде дуговой
стрелки, расчетной формулой является выражение
для касательного ускорения: a вр R
Вектор этого ускорения, называемого
вращательным ускорением, направляют
перпендикулярно радиусу в сторону дуговой
стрелки углового ускорения.

14.

Нормальное ускорение теперь
называется осестремительным
ε
ускорением aос 2 R
ω
aa
Его направляют по радиусу к оси
aa
v
вращения независимо от
направления дуговой стрелки
угловой скорости, не говоря уж о
направлении дуговой стрелки
углового ускорения.
Как следует из формул оба ускорения точки
пропорциональны расстоянию ее до оси
вращения (радиусу вращения).
- O
+
s
R
φ
nос
τ
вр

15.

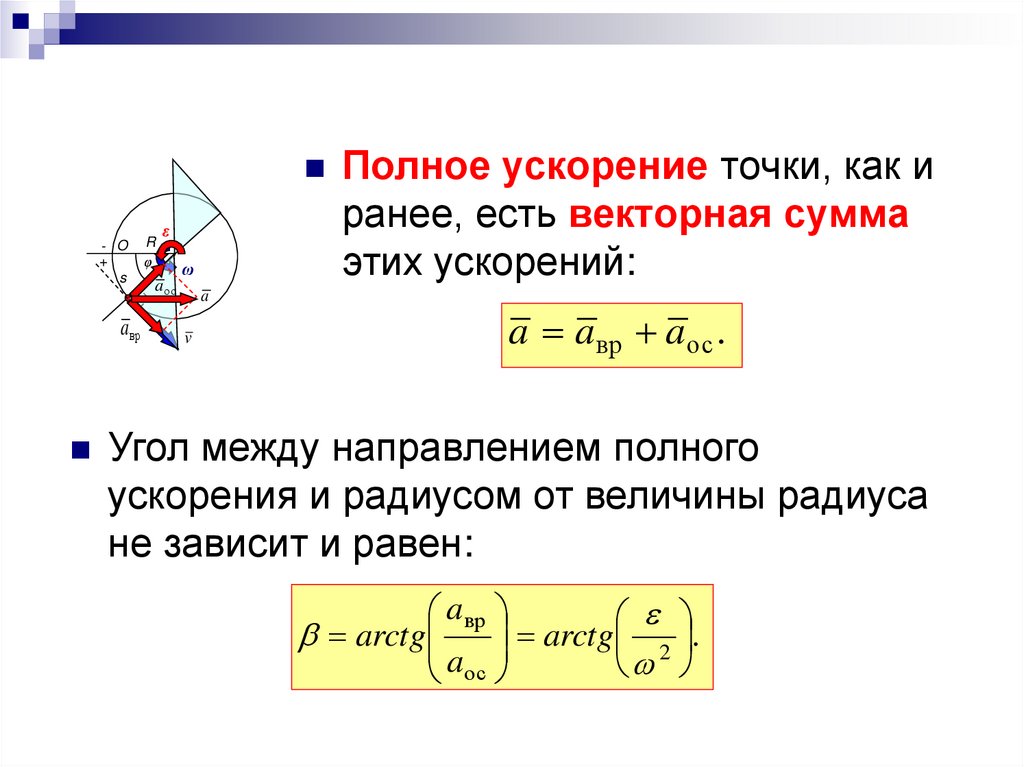
Полное ускорение точки, как и
- O
+
s
a вр
R
φ
ранее, есть векторная сумма
этих ускорений:
ε
a ос
ω
a
v
a a вр a ос .
Угол между направлением полного
ускорения и радиусом от величины радиуса
не зависит и равен:
aвр
arctg
arctg 2 .
aос

16.

Скорость и ускорения
точки при вращательном
движении как векторные
произведения.
Представим угловую
скорость и угловое ускорения
как векторы, направленные
по оси вращения в ту
сторону, откуда дуговые
стрелки этих величин
указывают вращение против
часовой стрелки.
z
z
ω
ω
ε
ε
k
k

17.

z
z
ω
ω
ε
ε
k
k
Положительное направление
оси z можно задать с помощью
единичного вектора k, тогда
векторы угловой скорости и
углового ускорения можно
представить как:
z k
zk
где z, z – проекции
соответствующих векторов на
ось z.

18.

Скорость точки при
ω
R
r
вращательном движении как
векторное произведение –
определяется выражением
v r
Оно описывает и величину, и
направление скорости.
Величина (модуль) этого векторного
произведения:
v r sin( , r ).
R
v R.

19.

Направление вектора
рассматриваемого векторного
произведения:
ω
R
r
v
по определению векторного
произведения – перпендикулярно
плоскости, проведенной через
умножаемые вектора, направлен в ту
сторону, откуда поворот первого
вектора ко второму на наименьший
угол кажется происходящим против
часовой стрелки;

20.

ω
R
r
v
по правилу правой руки: при совмещении
большого пальца с первым вектором,
остальных – со вторым вектором,
поворот большого пальца перпендикулярно
ладони указывает на направление вектора
векторного произведения.

21.

Таким образом, действительно
ω
R
r
v
векторное произведение
угловой скорости и радиусвектора полностью
определяет величину и
направление скорости точки
при вращательном движении в
соответствии с ранее
полученными результатами.

22.

Вращательное ускорение
точки как векторное
произведение – определяется
выражение
ε
R
r
a вр r
Оно описывает и величину, и
направление вращательного
ускорения.
Величина (модуль) этого векторного
произведения:
a вр r sin( , r ).
R
aвр R.

23.

Направление вектора
ε
R
r
a вр
рассматриваемого векторного
произведения можно
установить по определению
векторного произведения
или по правилу правой руки.
Таким образом, действительно векторное
произведение углового ускорения и
радиус-вектора полностью определяет
величину и направление вращательного
ускорения точки в соответствии с ранее
полученными результатами.

24.

ω
R
r
a ос
v
Осестремительное ускорение
точки как векторное произведение
– определяется выражением
aос v
Оно описывает и величину, и
направление осестремительного
ускорения.
Величина (модуль) этого векторного
произведения: aос v sin( , v ).
1, т.к. вектор скорости точки
перпендикулярен плоскости,
в которой лежит вектор
угловой скорости.

25.

Таким образом:
ω
R
r
a ос
v
v v ( R) 2 R.
Векторное произведение угловой скорости
и вектора скорости точки полностью
определяет величину и направление
осестремительного ускорения точки
Это векторное произведение может быть также
записано в виде:
aос ( r )

26.

z
ω
R
r
v
z
y
x
x
y
i
v r x
x
j
Формулы Эйлера – с
помощью раскрытия
векторного произведения для
скорости точки можно
получить общие
аналитические выражения
для этой скорости через
координаты рассматриваемой
точки при произвольной
расположении оси вращения
в пространстве:
k
y z ( y z z y )i ( z x x z ) j ( x y y x)k
y
z

27.

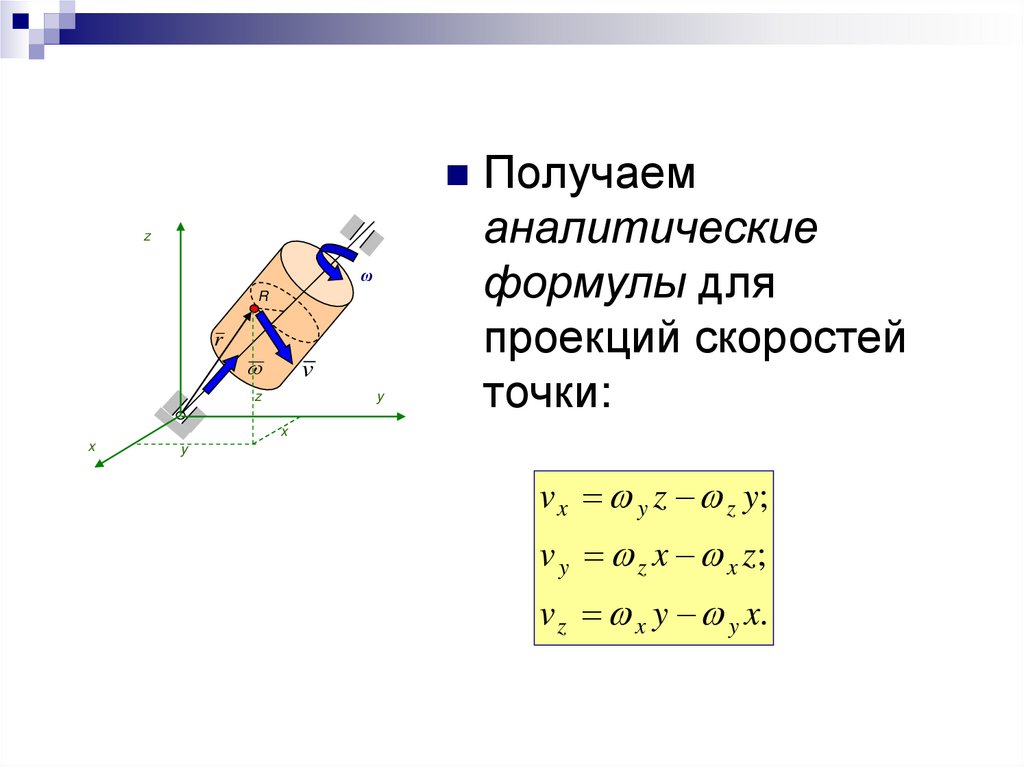
Получаем
z
ω
R
r
v
z
y
аналитические
формулы для
проекций скоростей
точки:
x
x
y
v x y z z y;
v y z x x z;
v z x y y x.

28.

Преобразования вращательных движений –
изменение величины и направление угловых
скоростей вращающихся звеньев в различных
передаточных механизмах:
фрикционное зацепление,
зубчатое зацепление,
ременная и цепная передачи

29. Фрикционное зацепление

v2
Скорости входящих в контакт
v1
ω2
ω1
R2
R1
точек колес при отсутствии
проскальзывания равны:
v1 v2 ; 1 R1 2 R2 .
1 R2
2 R1
Передаточное число, характеризующее изменение
скорости вращения при передаче вращения от одного
звена к другому – отношение угловой скорости
ведущего колеса к угловой скорости ведомого:
i1 2
1 R2
2 R1

30. Зубчатое зацепление

Число зубьев каждого из колес
прямо пропорционально радиусу
ω
колеса.
ω
Окружные скорости входящих в
R
R
контакт точек поверхностей зубьев
по-прежнему равны.
Полученные соотношения остаются
справедливыми, в том числе и для
случая внутреннего зацепления.
Радиусы делительных окружностей связаны с шагом
зубьев соотношениями: 2 R1 z1h 2 R2 z 2 h
С использованием чисел зубьев каждого из колес
1 z 2
имеем:
2
1
2
1
2
z1

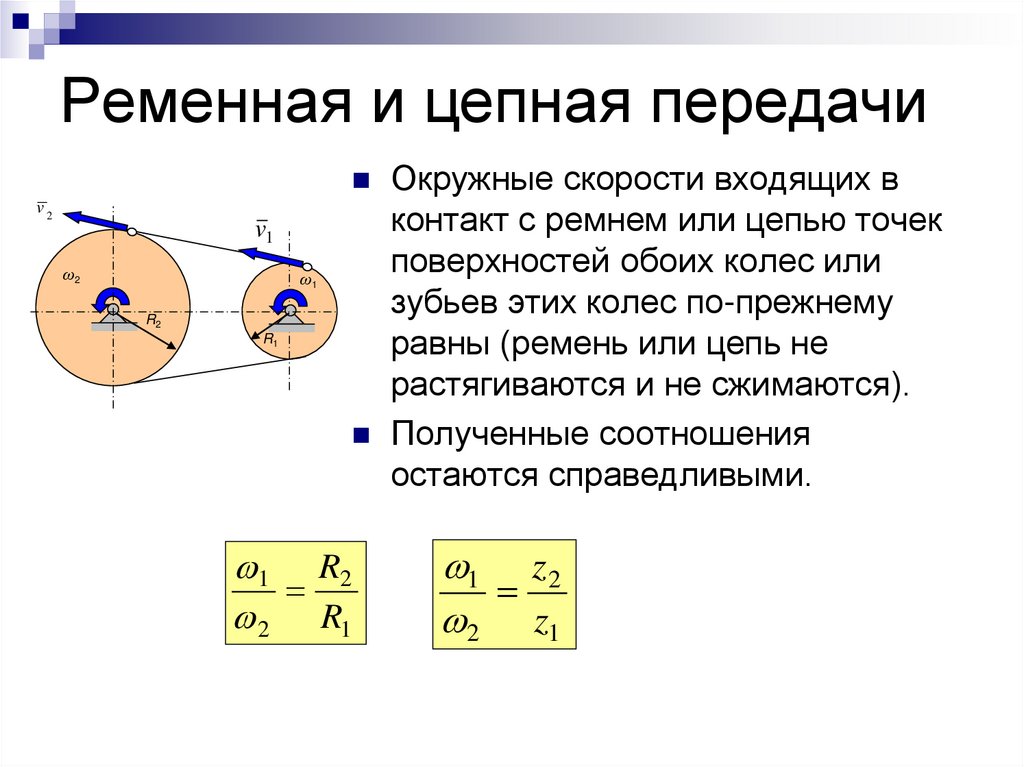
31. Ременная и цепная передачи

Окружные скорости входящих в
контакт с ремнем или цепью точек
поверхностей обоих колес или
зубьев этих колес по-прежнему
равны (ремень или цепь не
растягиваются и не сжимаются).
Полученные соотношения
остаются справедливыми.
v2
v1
ω2
ω1
R2
R1
1 R2
2 R1
1 z 2
2 z1

32. Спасибо за внимание!

Продолжение следует…