Similar presentations:
Кинематика
1. ГЛАВА I. МЕХАНИКА §§2‒3. Кинематика
О. И. ЛубенченкоНИУ МЭИ
Кафедра физики им. В. А. Фабриканта
2020
2. §2. Кинематика материальной точки
2Кинематика — раздел механики, изучающий механическое движение без
рассмотрения его причин.
I. Закон движения
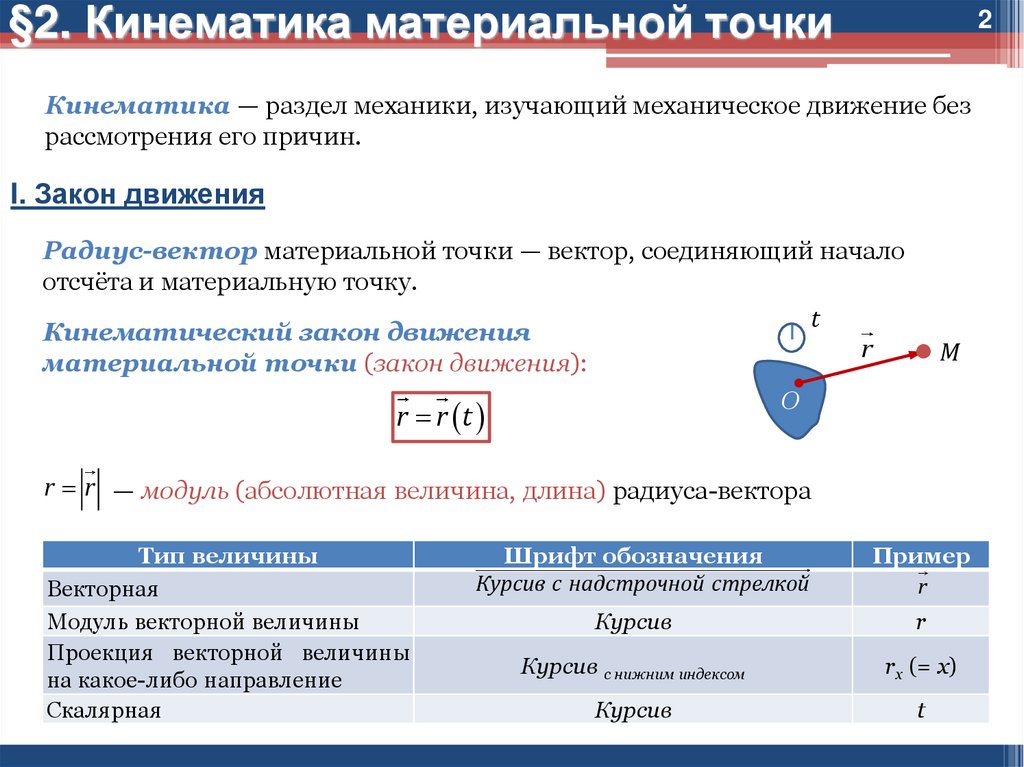
Радиус-вектор материальной точки — вектор, соединяющий начало
отсчёта и материальную точку.
t
Кинематический закон движения
r
M
материальной точки (закон движения):
O
r r t
r r — модуль (абсолютная величина, длина) радиуса-вектора
Тип величины
Векторная
Модуль векторной величины
Проекция векторной величины
на какое-либо направление
Скалярная
Шрифт обозначения
Курсив с надстрочной стрелкой
Пример
r
Курсив
r
Курсив с нижним индексом
rx (= x)
Курсив
t
3. §2. Кинематика материальной точки
II. Системы координат1. Декартова система координат
r
k
O
x
i
r xi y j zk
t
z
j
M
y
i , j , k — орты декартовой системы координат;
образуют правую тройку векторов.
x x t
y y t — кинематический закон движения
материальной точки в координатной
z
z
t
форме
Длина (модуль, абсолютная величина) радиуса-вектора
r x 2 y2 z2
3
4. §2. Кинематика материальной точки
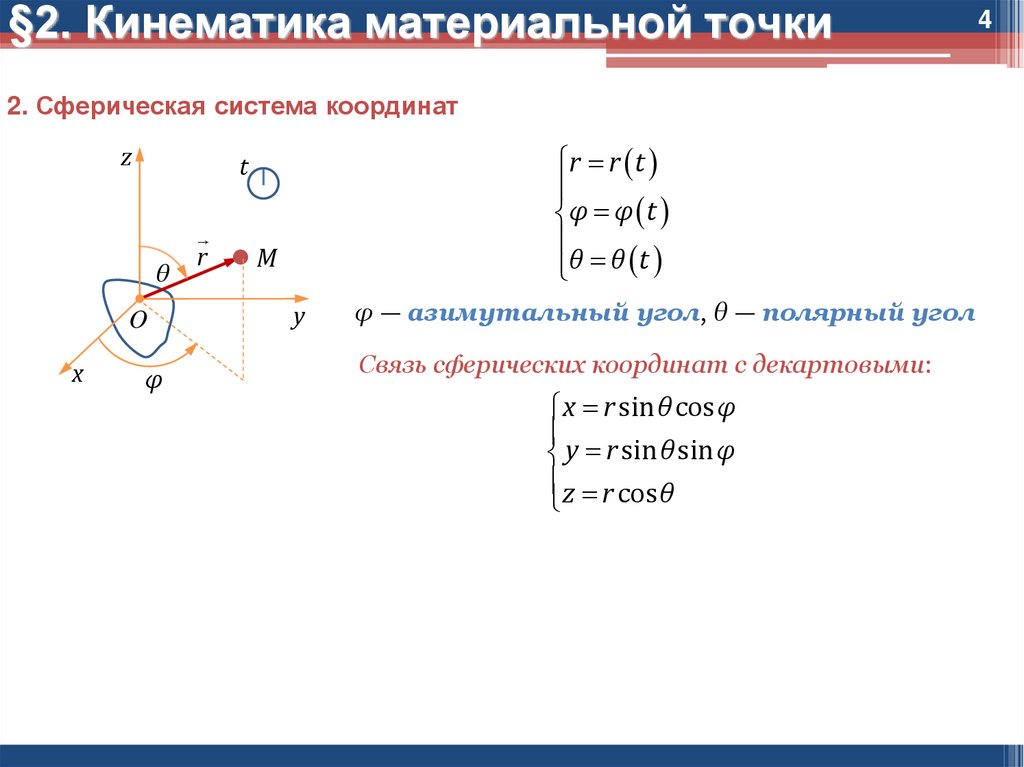
2. Сферическая система координатz
θ
O
x
r r t
φ φ t
θ θ t
t
φ
r M
y
φ — азимутальный угол, θ — полярный угол
Связь сферических координат с декартовыми:
x r sin θ cos φ
y r sin θ sin φ
z r cos θ
4
5. §2. Кинематика материальной точки
3. Цилиндрическая система координатz
M
r
z
y
O
x
ρ ρ t
φ φ t
z z t
t
φ
ρ
Связь цилиндрических координат с декартовыми:
x ρ cos φ
y ρ sin φ
z z
Частный случай: полярная система координат (при z = 0)
Результат решения задачи не должен зависеть от выбора системы
координат!
5
6. §2. Кинематика материальной точки
III. Кинематические параметры1. Перемещение
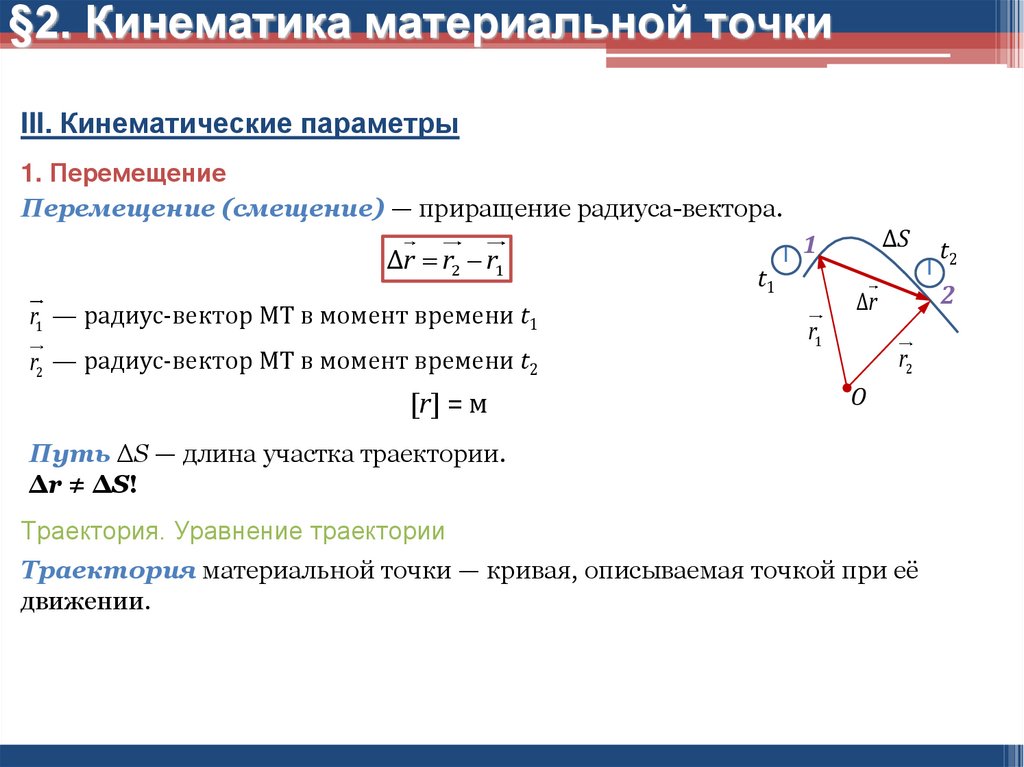
Перемещение (смещение) — приращение радиуса-вектора.
Δr r2 r1
r1 — радиус-вектор МТ в момент времени t1
r2 — радиус-вектор МТ в момент времени t2
[r] = м
ΔS
1
t1
2
Δr
r1
t2
r2
O
Путь ΔS — длина участка траектории.
Δr ≠ ΔS!
Траектория. Уравнение траектории
Траектория материальной точки — кривая, описываемая точкой при её
движении.
7. §2. Кинематика материальной точки
Для того чтобы найти уравнение траектории, нужно исключить время изкинематического закона движения в координатной форме:
(для двумерного движения)
x x t
y y x
y y t
2. Скорость
Скорость — векторная ФВ, характеризующая быстроту движения.
Средняя скорость
v
Δr
Δt
м
v с
Δt = t2 – t1
Мгновенная скорость
Δr dr
r rt
Δt 0 Δt
dt
v lim
Вектор мгновенной скорости направлен по касательной к траектории.
8. §2. Кинематика материальной точки
Средняя путевая скоростьvпут
ΔS
Δt
Δr
Δx i Δy j Δz k
lim
Δt 0 Δt
Δt 0
Δt
Δx
Δy
Δz
dx dy
dz
lim i lim
j lim k i
j k
Δt 0 Δt
Δt 0 Δt
Δt 0 Δt
dt
dt
dt
v lim
dx
v
x dt
dy
v
y
dt
dz
v
z dt
v v2x v2y v2z
v
dr
dt
9. §2. Кинематика материальной точки
Обратная задачаДано v t , найти r t .
За малое время dt материальная точка совершает перемещение dr v dt .
Просуммируем все малые перемещения, т. е. проведём интегрирование по
времени:
t
r r0 v t dt
0
r0 — начальный радиус-вектор
3. Ускорение
Ускорение — векторная ФВ, характеризующая скорость изменения скорости
материальной точки.
Среднее ускорение
a
Δv
Δt
м
a с2
10. §2. Кинематика материальной точки
Мгновенное ускорениеΔv d v
d2 r
a lim
v vt 2 r rt
Δt 0 Δt
dt
dt
d vx d 2 x
ax dt dt 2
dv y d2 y
2
a y
dt
dt
d vz d 2 z
2
az
dt dt
a ax i a y j az k
Обратная задача
Дано a t , найти v t , r t .
t
v t v0 a t dt
0
t
t
t
0
0
0
r t r0 v t dt r0 v0t dt a t dt
r0 — начальный радиус-вектор, v0 — начальная скорость
11. §2. Кинематика материальной точки
ПРИМЕР РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ1) Равномерное движение: v const
a 0
t
r r0 vdt r0 vt
0
2) Равноускоренное движение: a const
t
v t v0 adt v0 at
0
t
r r0
0
at 2
v0 at dt r0 v0t
2
IV. Криволинейное движение
Орты естественной системы координат
τ1 v1
τ — единичный вектор, направленный по
t1
t2
1
касательной к траектории по направлению
n2
v2 движения
n1
n — единичный вектор, направленный по
2 τ2
нормали к траектории в сторону её вогнутости
v vτ τ 0n vτ a aτ τ an n
a
d v dv
dτ
τ v
dt dt
dt
12. §2. Кинематика материальной точки
τ1ρ — радиус кривизны траектории
Δl ρΔα
ρ
O
Δα
Δl
ρ
τ2
Δα
τ1
Δτ
Δτ
Δτ τΔα
Δτ τ2 τ1
Δl
ρ
Δτ
Δl
n
ρ
При Δt → 0
dl
dτ n
ρ
dv
v2
a
τ n
dt
ρ
dv
aτ
dt
v
dτ dl
v
n n
dt ρdt
ρ
v2
an
ρ
aτ — тангенциальное (касательное) ускорение
an — нормальное (центростремительное) ускорение
a aτ2 an2
13. §3. Кинематика твёрдого тела
I. Виды движения• Поступательное движение — движение, при котором любая
прямая, соединяющая две точки движущегося тела, перемещается
параллельно самой себе.
• Вращение вокруг неподвижной оси (вращательное движение)
— движение, при котором все точки тела движутся по окружностям,
лежащим в параллельных плоскостях, таким, что центры этих
окружностей лежат на одной прямой, называемой осью вращения.
• Плоское движение — движение, при котором все точки тела движутся
в параллельных плоскостях.
Плоское движение = поступательное движение + вращательное движение.
• Сферическое движение (вращение вокруг неподвижной точки)
— движение, при котором все точки тела движутся по сферам, центры
которых находятся в одной точке, называемой центром вращения.
• Другие случаи – сложное движение.
14. §3. Кинематика твёрдого тела
II. Угловые кинематические параметрыВекторы
полярные
(истинные)
имеют точку приложения
r v F p
аксиальные
(псевдовекторы)
не имеют точки приложения
Δφ ω M L
1. Угловое перемещение
Вектор углового перемещения Δφ для малых
z
угловых перемещений
Направление — по правилу правого винта.
Δφ
Δφ k
k
A
r
O
Δφ
A’
Δφ Δφz k
Угол φ — скалярная ФВ, характеризующая поворот
тела.
Закон вращательного движения твёрдого тела
φz φz t
15. §3. Кинематика твёрдого тела
1[φ] = рад (радиан)
π
рад
180
2. Угловая скорость
Угловая скорость — векторная ФВ, характеризующая быстроту и
направление вращения.
dφ
ω
dt
ω
рад 1
с
с
3. Угловое ускорение
Угловое ускорение — векторная ФВ, характеризующая быстроту и
направление изменения угловой скорости.
рад 2
ε с2 с
При вращении вокруг неподвижной оси Δφ ω ε k
dω d 2 φ
ε
2
dt dt
16. §3. Кинематика твёрдого тела
4. Частота вращенияЧастота вращения — скалярная положительная ФВ, характеризующая
быстроту вращения, равная числу оборотов тела вокруг оси вращения за
единичный промежуток времени.
ν
ω
2π
ν
об 1
с
с
5. Период вращения
Период вращения — скалярная положительная ФВ, характеризующая
быстроту вращения, равная времени, за которое вращающееся тело
совершает один полный оборот вокруг оси вращения.
T
1 2π
ν ω
T с
17. §3. Кинематика твёрдого тела
III. Связь между линейными и угловыми кинематическими параметрамиz
t + Δt
ω
O
r
v
⊗M
ΔS
ΔS rΔφ
ΔS rΔφ
v
ω r
Δt
Δt
При Δt → 0 v ωr
t
Δφ M
z⊙ r
v ωr
0
v ωr sin ω, r
d v d ωr
dω
dr
aτ
r
ω εz r
dt
dt
dt
dt
v2 ω2r 2
an
ω2r
r
r
dr
a εr ω
dt
a εr ωv εr ω ωr
Для сложного движения v vC ω r r C
r C — радиус-вектор центра масс
vC — скорость центра масс














 physics
physics








