Теоретическая механика. Кинематика

1.

ТЕОРЕТИЧЕСКА
Я МЕХАНИКА
КИНЕМАТИКА

2. Лекция 6

Сферическое движение твердого тела –
одна из точек тела остается неподвижной
во время движения. Остальные точки
движутся по сферическим поверхностям,
центры которых совпадают с неподвижной
точкой.
Углы Эйлера – используются для
описания сферического движения
твердого тела посредством ввода двух
систем координат.

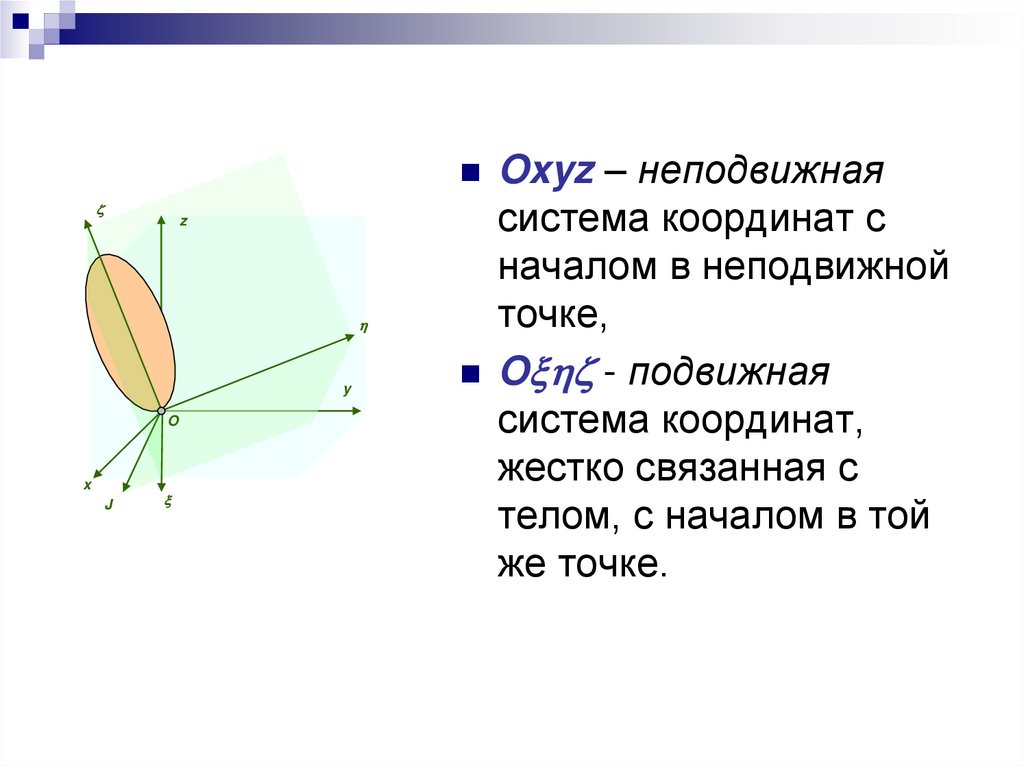
3.

Oxyz – неподвижная
z
y
O
x
J
система координат с
началом в неподвижной
точке,
O - подвижная
система координат,
жестко связанная с
телом, с началом в той
же точке.

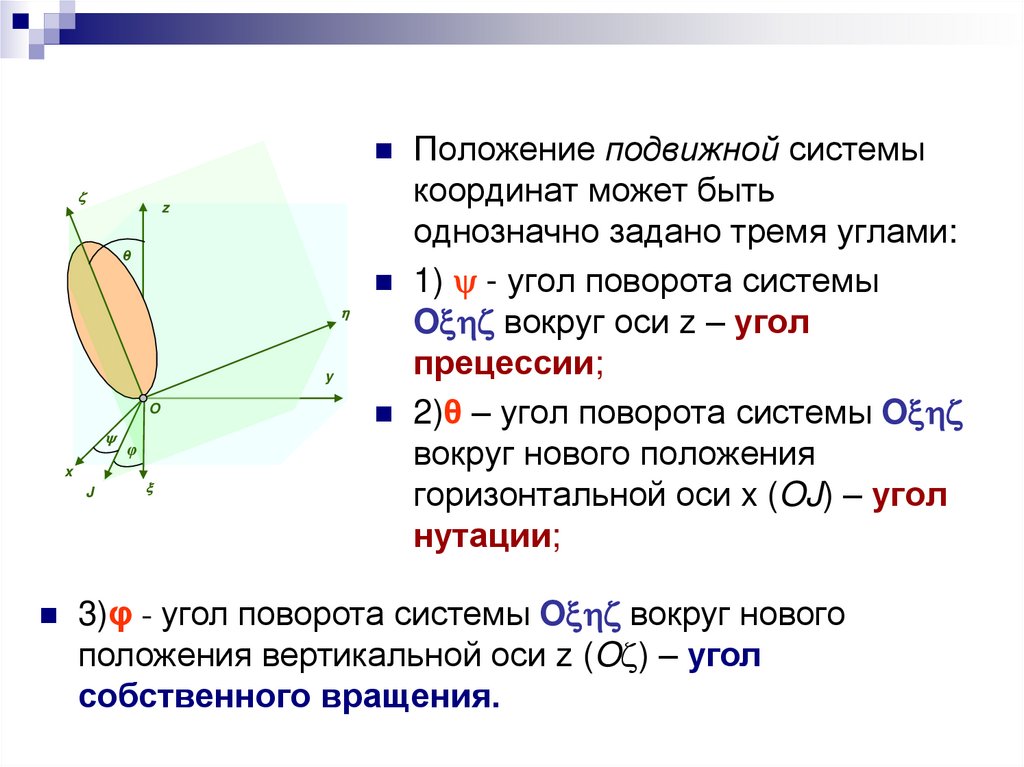
4.

Положение подвижной системы
координат может быть
однозначно задано тремя углами:
1) - угол поворота системы
O вокруг оси z – угол
прецессии;
2)θ – угол поворота системы O
вокруг нового положения
горизонтальной оси x (OJ) – угол
нутации;
z
θ
y
O
x
J
φ
3)φ - угол поворота системы O вокруг нового
положения вертикальной оси z (O ) – угол
собственного вращения.

5.

Уравнения
z
θ
y
O
x
J
φ
сферического
движения твердого
тела:
(t );
(t );
(t ).

6. Теорема Эйлера

Твердое тело,
O
имеющее одну
неподвижную точку,
можно переместить из
одного положения в
другое одним
поворотом вокруг
некоторой оси,
проходящей через эту
точку.

7.

Рассмотрим дугу большого
A
O
B
круга AB, находящейся на
сферической поверхности.
Дуга большого круга – дуга
наименьшей кривизны на
поверхности (часть
окружности, полученной
сечением плоскости,
проходящей через центр).
Далее будет подразумеваться,
что все дуги есть дуги
большого круга.

8.

Пусть AB
A
O
B
D
C
A1
B1
переместилась в
положение A1B1.
Проведем дуги AA1 и
ВB1.
Из середин С и D дуг
AA1 и ВB1 проведем
дуги, перпендикулярные
к дугам AA1 и ВB1.

9.

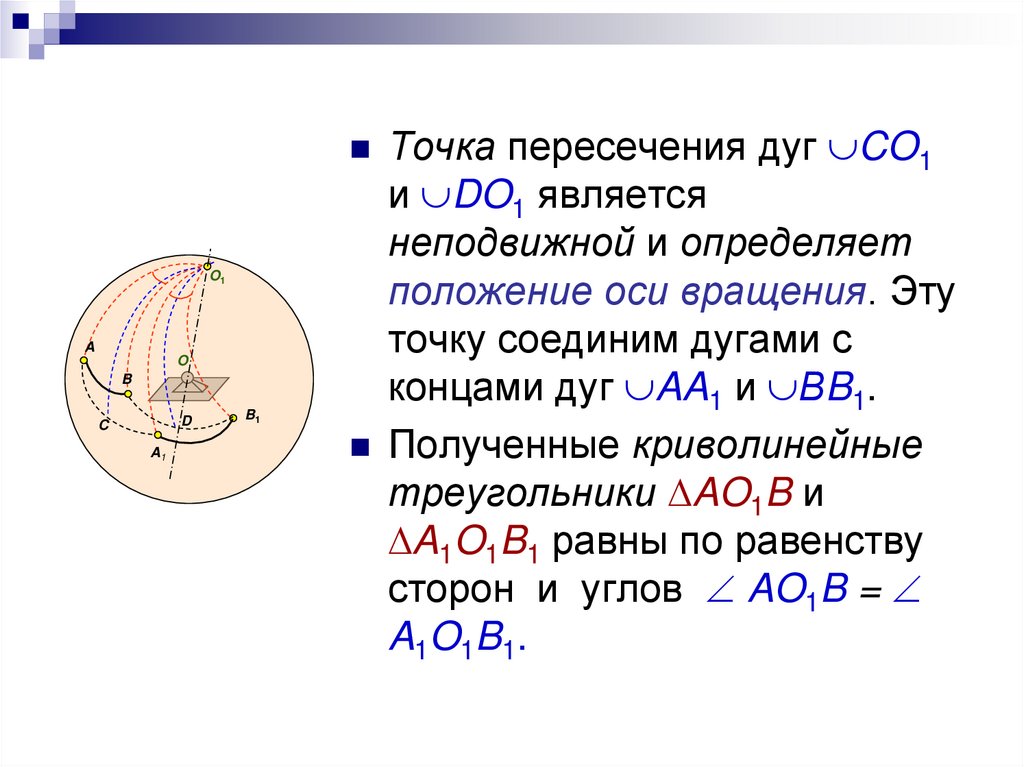
Точка пересечения дуг CO1
O1
A
O
B
D
C
A1
B1
и DO1 является
неподвижной и определяет
положение оси вращения. Эту
точку соединим дугами с
концами дуг AA1 и ВB1.
Полученные криволинейные
треугольники AO1B и
A1O1B1 равны по равенству
сторон и углов AO1B =
A1O1B1.

10.

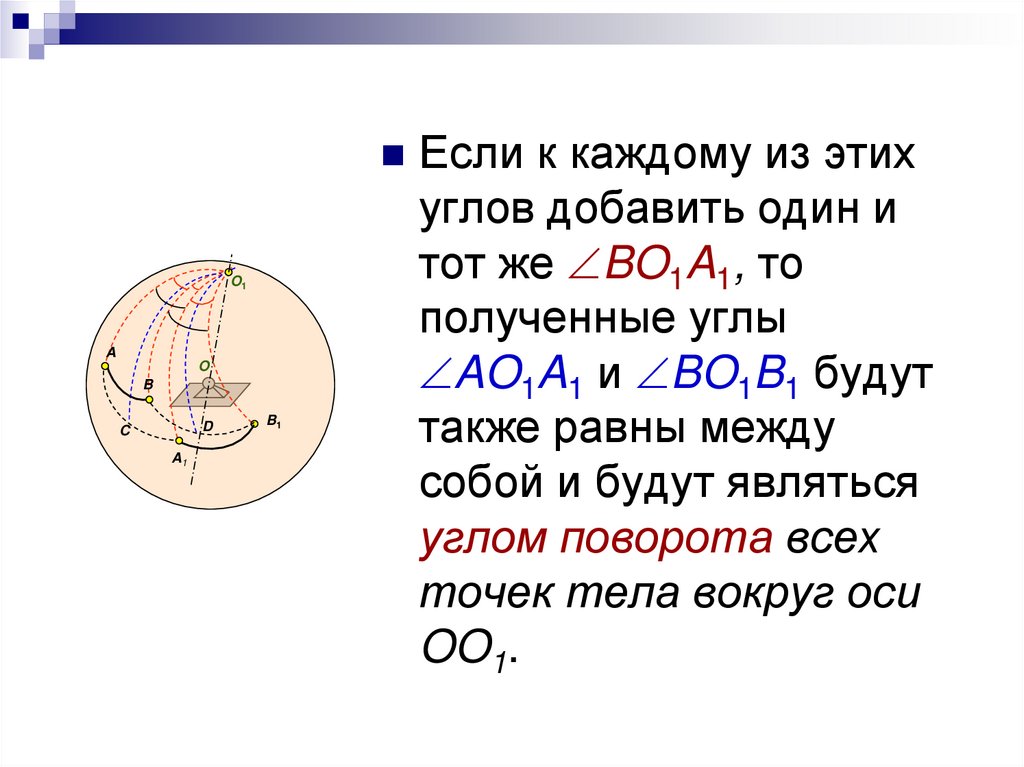
Если к каждому из этих
O1
A
O
B
D
C
A1
B1
углов добавить один и
тот же BO1A1, то
полученные углы
AO1A1 и BO1B1 будут
также равны между
собой и будут являться
углом поворота всех
точек тела вокруг оси
OO1.

11.

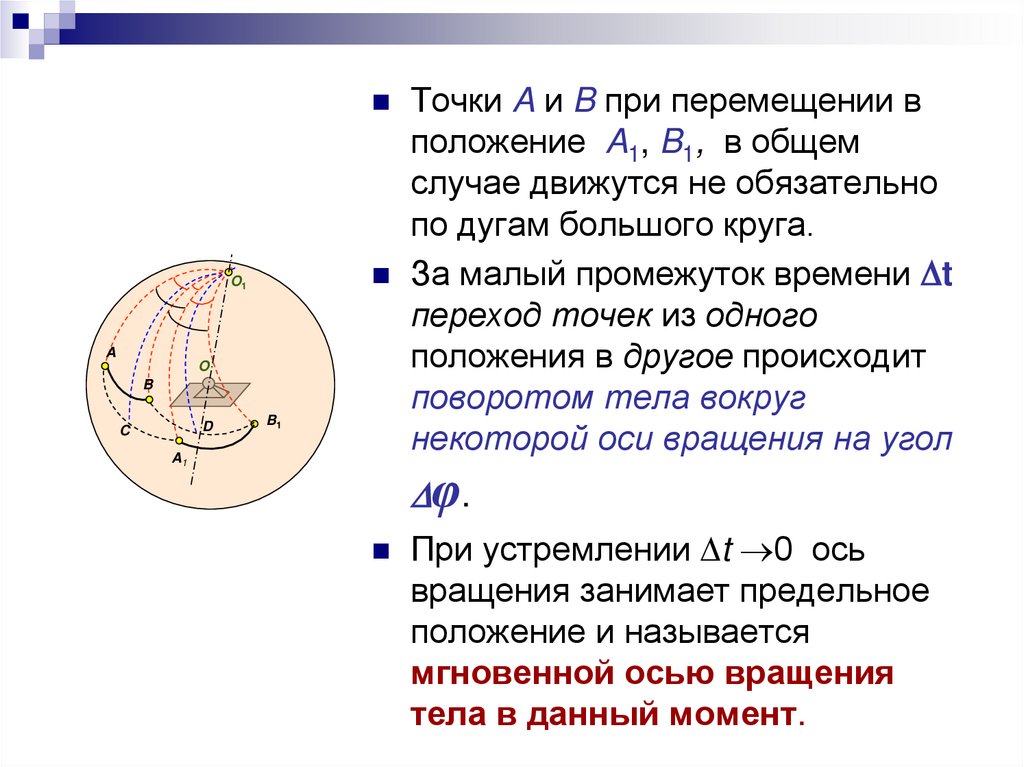
Точки A и B при перемещении в
положение A1, B1, в общем
случае движутся не обязательно
по дугам большого круга.
За малый промежуток времени t
переход точек из одного
положения в другое происходит
поворотом тела вокруг
некоторой оси вращения на угол
O1
A
O
B
D
C
A1
B1
φ.
При устремлении t 0 ось
вращения занимает предельное
положение и называется
мгновенной осью вращения
тела в данный момент.

12.

Угловая скорость
O
сферического
движения твердого
тела – вектор,
направленный вдоль
мгновенной оси
вращения, модуль
которого равен:
Δ d
Δt lim 0
.
Δt
dt

13.

Угловое ускорение сферического
движения твердого тела –
характеризует изменение вектора
угловой скорости:
O
t
;
t1 t Δt 1 Δ ;
1
ср
Δ
ср
Δt
- среднее угловое
ускорение в интервале времени t
Угловое ускорение в момент
времени t:
Δ d
Δt lim 0
.
Δt
dt

14.

Вектор угловой скорости с
O
началом в неподвижной точке
при движении тела изменяется
подобно радиусу-вектору точки,
движущейся в пространстве по
некоторой траектории.
Вектор скорости этой точки
направлен по касательной к
траектории и определяется
выражением:
v
dr
dt

15.

Траектория конца вектора
O
угловой скорости с
началом в неподвижной
точке при движении тела
описывает кривую,
называемую годографом
вектора угловой скорости.

16.

Сравнивая выражения для
u
O
d
.
dt
E
вектора углового ускорения тела
и вектора скорости точки можно
установить, что угловое
ускорение тела геометрически
равно линейной скорости конца
вектора угловой скорости.
Прямая, по которой направлен
вектор углового ускорения,
называется осью мгновенного
углового ускорения (E).

17.

Скорость точки твердого
z
h
v
r
O
x
Ω
y
тела при сферическом
движении – определяется
как вращательная скорость
вокруг мгновенной оси:
v r
v r sin( , v ) h Ω .
i
j
v r x
x
y
y
( y z z y )i
z ( z x x z ) j
z
( x y y x)k
k

18.

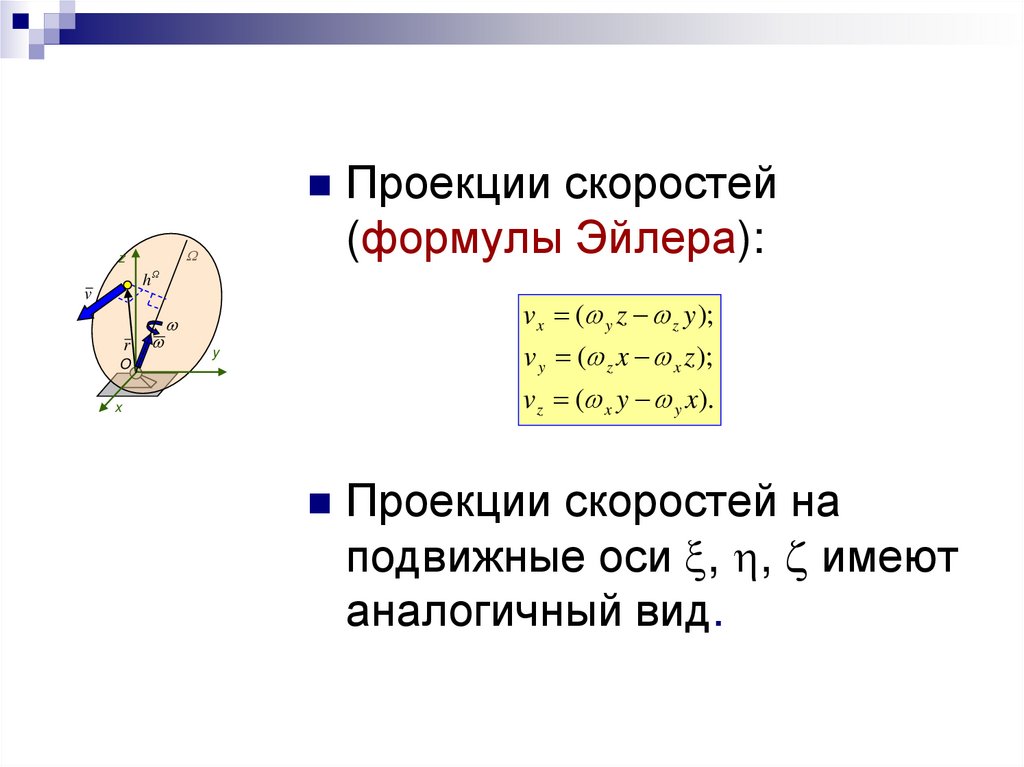
Проекции скоростей
(формулы Эйлера):
z
hΩ
v
r
O
x
y
v x ( y z z y );
v y ( z x x z );
v z ( x y y x).
Проекции скоростей на
подвижные оси , , имеют
аналогичный вид.

19.

Мгновенная ось вращения
z
h
v
r
O
x
Ω
y
в данное мгновение –
геометрическое место точек
с нулевой скоростью.
Уравнение мгновенной оси
получается приравниванием
проекций скоростей нулю:
v x ( y z z y ) 0;
v y ( z x x z ) 0;
v z ( x y y x) 0.
y z z y;
z x x z;
x y y x.
x
x
y
y
x
z
.

20.

Ускорение точки твердого тела
при сферическом движении:
z
h
v
r
O
x
a
Ω
dv d
d
dr
( r )
r
r v aврE aосΩ .
dt dt
dt
dt
Ускорение точки равно
y
геометрической сумме
вращательного ускорения
относительно оси мгновенного
углового ускорения (E) и
осестремительного ускорения
относительно мгновенной оси
вращения ( ).
Ω
a aврE aос
aврE r
Ω
aoc
( r )

21.

Модуль вращательного
ускорения равен:
E
aвр
hE
z
hΩ
v
E
a врE r
O
x
h
E
y
где hE – длина перпендикуляра,
опущенного на ось мгновенного
ускорения E.
Вектор вращательного ускорения
направлен перпендикулярно
радиусу вращения (hE) в сторону
дуговой стрелки углового
ускорения.

22.

Модуль осестремительного
ускорения равен:
z
hΩ
v
a врE r
O
x
Ω
aос
2 hΩ
h
Ω
aос
E
E
y
где h – длина
перпендикуляра, опущенного
на мгновенную ось вращения
.
Вектор осестремительного
ускорения направлен по
радиусу вращения (h ) к
мгновенной оси вращения.

23.

h
v
a врE r
O
x
Модуль полного ускорения
z
h
E
Ω
Ω
aос
E
равен:
y
E 2
Ω 2
E Ω
Ω
a (aвр
) (aoc
) 2aвр
aoc cos( aврE , aoc
)

24.

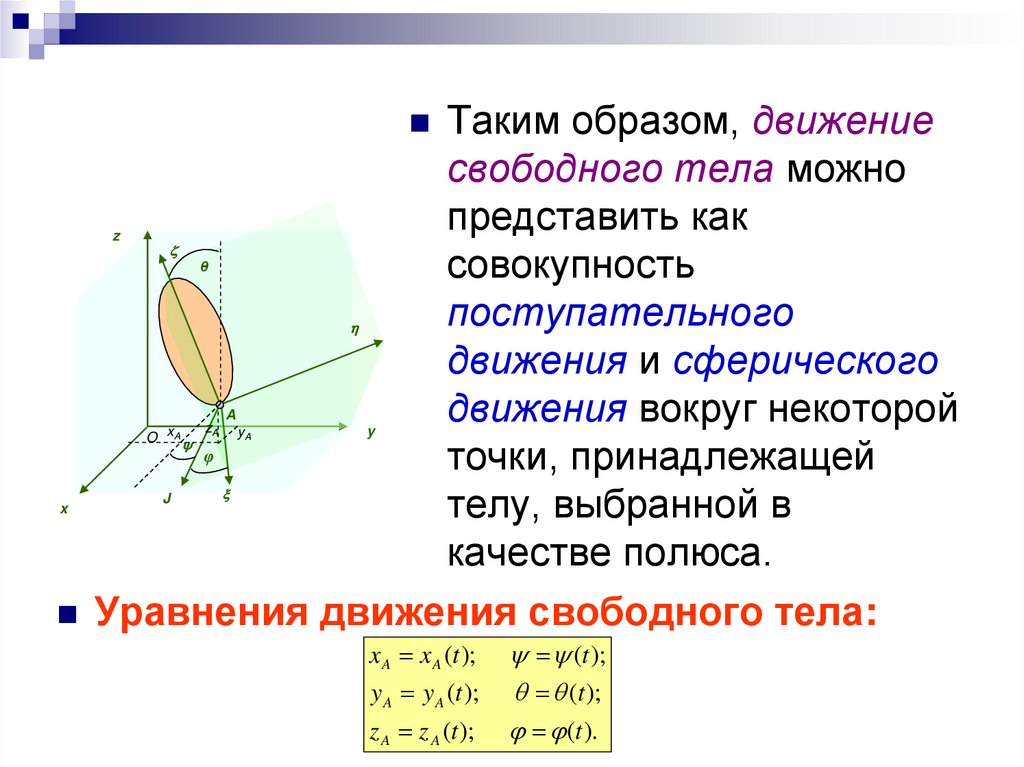
Общий случай движения твердого
тела – Положение тела в пространстве
однозначно определяется положением
трех его точек, не лежащих на одной
прямой. По трем точкам можно
построить треугольник, который и
будет далее представлять тело в
пространстве.

25.

Разложение движения
C1
B1
A1
C’
C
A
свободного твердого тела
– Как и в случае плоского
движения существует
бесчисленное множество
способов представления
движения свободного тела в
виде совокупности двух,
более простых движений.

26.

Например, можно перевести
C1
B1
A1
C’
C
A
тело из исходного положения,
обозначенное треугольником
ABC, в другое положение,
соответствующее треугольнику
A1B1C1, поступательным
перемещением в положение
A1B’C’, а затем поворотом
его вокруг некоторой оси,
проходящей через точку,
выбранной в качестве полюса,
например, точку A1.

27.

Или, напротив, вначале
C1
C’
B1
A1
A
B’
C
B
повернуть треугольник ABC
вокруг некоторой оси,
проходящей через точку,
выбранной в качестве полюса,
например, точку A, чтобы
стороны треугольника ABC
стали параллельными
сторонам треугольника
A1B1C1, а затем перевести
треугольник AB’C
поступательным движением
в положение A1B1C1:

28.

Таким образом, движение
z
θ
O xA
x
J
zA
A
yA
φ
y
свободного тела можно
представить как
совокупность
поступательного
движения и сферического
движения вокруг некоторой
точки, принадлежащей
телу, выбранной в
качестве полюса.
Уравнения движения свободного тела:
x A x A (t );
y A y A (t );
z A z A (t );
(t );
(t );
(t ).

29.

Скорость точки свободного
B
z
rAB
rB
rA
O
x
A
y
тела – Скорость любой точки
тела равна геометрической
сумме скорости полюса и
скорости этой точки в ее
сферическом движении вокруг
полюса.
Радиусы-векторы точек A и B
связаны между собой
соотношением:
rB (t ) rA (t ) rAB (t ).

30.

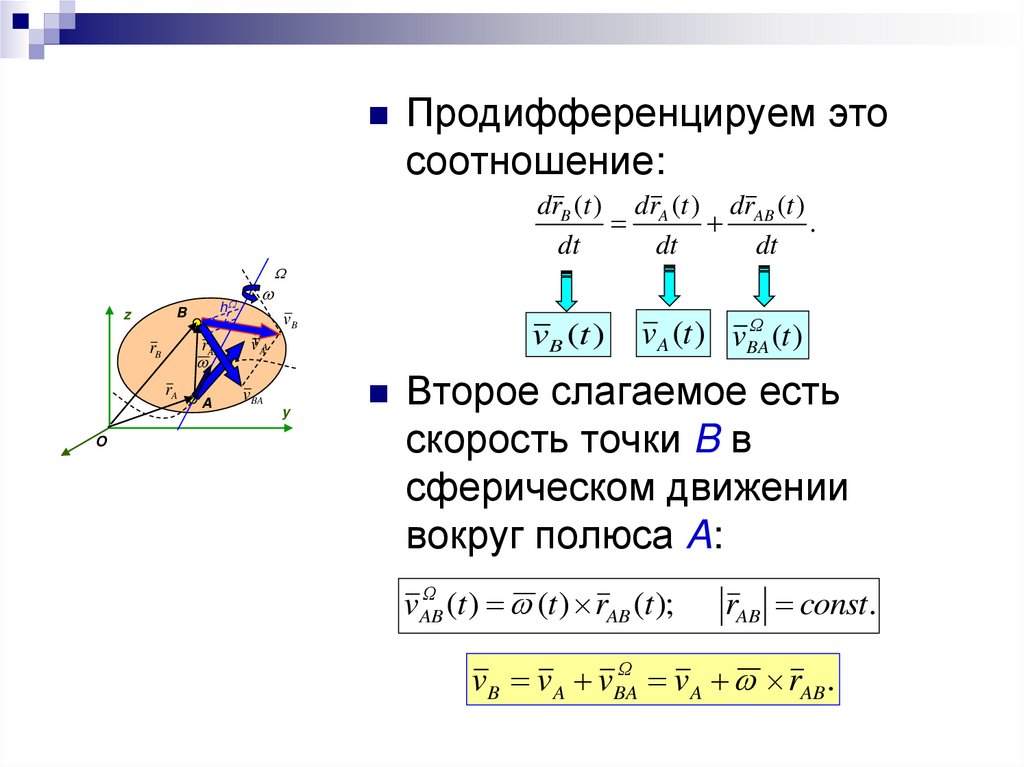
Продифференцируем это
соотношение:
drB (t ) drA (t ) drAB (t )
.
dt
dt
dt
rAB
rB
rA
O
h
B
z
A
vB
vvAA
vBA
y
vB (t )
Ω
v A (t ) vBA
(t )
Второе слагаемое есть
скорость точки B в
сферическом движении
вокруг полюса A:
Ω
vAB
(t ) (t ) rAB (t );
rAB const.
Ω
vB v A vBA
v A rAB .

31.

Полученное соотношение полностью совпадает
с теоремой о сложении скоростей для плоского
движения.
Разница состоит лишь в том, что используется
не центр вращения, а ось мгновенного
вращения .
Отсюда имеют место и аналогично
доказываются следствия о равенстве проекций
скоростей точек на ось, проходящих через эти
точки, и о пропорциональности отрезков
линии, проходящей через концы векторов
скоростей.

32.

В дополнение к этим двум следствиям
из теоремы о сложении вытекает третье
следствие:
Скорости точек свободного тела,
лежащих на прямой, параллельной
мгновенной оси, геометрически
равны.
Справедливость утверждения следует
из равенства скоростей этих точек
во вращении вокруг мгновенной оси.

33. Независимость векторов угловой скорости и углового ускорения от выбор полюса.

2
1
A
vA
vO 1
r1
1
O1
r2
vO 2
O2
2
Запишем теорему о
сложении скоростей для
одной и той же точки A с
использованием
различных полюсов O1 и
O 2:
v A vO1 1 r1 ; (a)
v A vO 2 2 r2 ; (b)

34.

Свяжем между собой
2
1
A
vA
vO 1
r1
1
r2
vO 2
r12
O1
O2
2
полюсы O1 и O2 радиусомвектором r12 и выразим
скорость второго полюса
через скорость первого:
r1 r12 r2 ;
vO 2 vO1 1 r12 .
Подставим это выражение
в формулу (b):
v A (vO1 1 r12 ) 2 r2 . (c)

35.

Приравняем правые части (a) и
2
1
vO1 1 r1 vO1 1 (r1 r2 ) 2 r2 .
A
vA
vO 1
r1
1
r2
vO 2
r12
O1
O2
(c), и учтем соотношение между
радиусами-векторами:
2
После некоторых сокращений и
преобразований получаем:
1 r1 1 r1 1 r2 2 r2 .
1 r2 2 r2 .
Отсюда следует равенство
угловых скоростей: 1 2 .

36.

Продифференцируем
полученное равенство:
d 1 d 2
,
dt
dt
2
1
Итак, векторы угловой
A
vA
vO 1
r1
1
r2
vO 2
r12
O1
1
O2
2
1 2 .
2
E2
E1
скорости и углового
ускорения не зависят от
выбора полюса.
Выбор полюса влияет лишь на
величину вектора скорости
поступательного движения
при разложении движения
свободного тела.

37.

Ускорение точки свободного тела –
Ускорение любой точки тела равна
геометрической сумме
ускорения полюса и
ускорения этой точки в ее
сферическом движении вокруг полюса.

38.

Запишем теорему о
z
rAB
A
O
x
h
B
vB
vA
сложении скоростей:
vB vA rAB .
Продифференцируем
vBA
y
это соотношение:
dvB dv A d
dv
d
dr
( rAB ) A
rAB AB .
dt
dt dt
dt
dt
dt
Ω
aB a A rAB vBA
.

39.

Ω
aB a A rAB vBA
.
E
a BA
hE
B
z
a
Ω
BA h
E
hE
aA
O
x
rAB
E
aBA
A
y
Ω
aBA
2 hΩ
Здесь вектор aA – ускорение
полюса.
Второе слагаемое –
вращательное ускорение точки
B в сферическом движении
относительно полюса A.
Третье слагаемое –
осестремительное ускорение
точки B в сферическом движении
относительно полюса A.

40.

Геометрическая сумма
B
z
Ω
aBA
h
E
hE
aA
O
x
rAB
E
aBA
A
y
вращательного и
осестремительного
ускорений точки в
сферическом движении
есть полное ускорение
точки в сферическом
движении вокруг полюса:
сф
E
Ω
aBA
aBA
aBA
Таким образом:
сф
a A aB aBA
.

41. Спасибо за внимание!

Продолжение следует…