Теоретическая механика. Кинематика. Лекция 4

1.

ТЕОРЕТИЧЕСКА
Я МЕХАНИКА
КИНЕМАТИКА

2. Лекция 4

Плоскопараллельное
движение твердого тела –
движение, при котором
каждая точка тела
движется в плоскости,
параллельной некоторой
неподвижной плоскости.
Сечение тела одной из таких плоскостей есть плоская
фигура, остающаяся в этой плоскости пр и движении
тела.

3.

Теорема о плоскопараллельном
движении твердого тела –
плоскопараллельное движение
твердого тела однозначным образом
определяется движением плоской
фигуры, образованной сечением
тела одной из параллельных
плоскостей.

4.

Выберем две точки на
M1
r1 M 1 M 2
M2
O
r2
произвольных двух
сечениях тела,
находящиеся на одном
перпендикуляре к этим
плоскостям.
Проведем к каждой точке радиусы-векторы
из неподвижной точки O и свяжем их между
собой вектором M1M2:
r2 r1 M 1 M 2

5.

M1
r1 M 1 M 2
M2
O
r2
При плоском движении тела
вектор M1M2 не изменяется
по величине, остается
параллельным самому себе
(движется поступательно) и,
следовательно, точки этого
вектора описывают
тождественные
траектории и имеют в
каждый момент времени
одинаковые скорости и
ускорения:
dr2 dr1
d 2 r2 d 2 r1
; (M 1M 2 const ); v2 v1 , и
2 ; a2 a1 .
2
dt
dt
dt
dt

6.

M1
r1 M 1 M 2
M2
O
r2
Таким образом, при плоском движении
тела движение каждой точки одной из
плоских фигур определяет движение
соответствующих точек,
находящихся во всех других смежных
параллельных плоскостях.

7.

Следствие: Поскольку положение плоской
фигуры однозначно определяется
положением ее двух точек или отрезка
прямой, проведенной через эти точки, то
плоскопараллельное движение твердого
тела определяется движением
прямолинейного отрезка, принадлежащего
одному из сечений тела параллельными
плоскостями.

8. Разложение плоскопараллельного движения плоской фигуры на поступательное и вращательное движения

Плоскую фигуру или отрезок
B
A2
B2
A
прямой можно перевести из
одного положения в другое
бесчисленным множеством
способов, меня
последовательность
выполнения
поступательного и
вращательного движения
между собой, а также выбирая
различные траектории и
точки в качестве полюса

9.

A1
B
xC
A2
yC
A
B1
B2
Таким образом,
плоскопараллельное
движение состоит из двух
движений:
поступательное и
вращательное, и его
всегда можно разложить
на эти два движения.
При этом поступательное зависит от выбора полюса
и траектории движения, а вращательное,
характеризуемое поворотом вокруг выбранного
полюса, не зависит от выбора полюса (для любого
полюса величина угла поворота и направление
вращения – одинаковы).

10. Уравнение движения плоской фигуры:

Выбирая в качестве
полюса любую точку,
например, A,
поступательная часть
движения будет
описываться уравнениями
движения этой точки.
Вращательная часть движения описывается
уравнением изменения угла поворота вокруг
полюса: x A x A (t );
y
B
xA
A
yA
x
y A y A (t );
(t ).

11.

Уравнения движения
y
B
xA
A
yA
x
любой точки плоской
фигуры, положение,
которой задается
координатами локальной
системы отсчета,
связанной с фигурой:
xC x A (t ) xC cos (t ) yC sin (t );
yC y A (t ) xC sin (t ) yC cos (t ).

12. Независимость угловой скорости плоской фигуры от выбора полюса

Выберем два произвольных
D
A
A
B
B
С
A B
прямолинейных отрезка,
изображающих положение
плоской фигуры и два полюса
на этих отрезках
Углы наклона отрезков к горизонтальной оси
различны и связаны между собой
соотношением:
B (t ) A (t ) .

13. Независимость угловой скорости плоской фигуры от выбора полюса

D
A
A
B
B
С
A B
Продифференцируем
соотношение:
d B (t ) d A (t )
, (α const ).
dt
dt
Отсюда следует, что угловые скорости
двух отрезков равны:
CA DB .

14. Независимость углового ускорения плоской фигуры от выбора полюса

D
A
A
B
С
A B
B
d CA d DB
.
dt
dt
После повторного
дифференцирования
следует, что угловые
ускорения двух
отрезков также равны:
CA DB .

15.

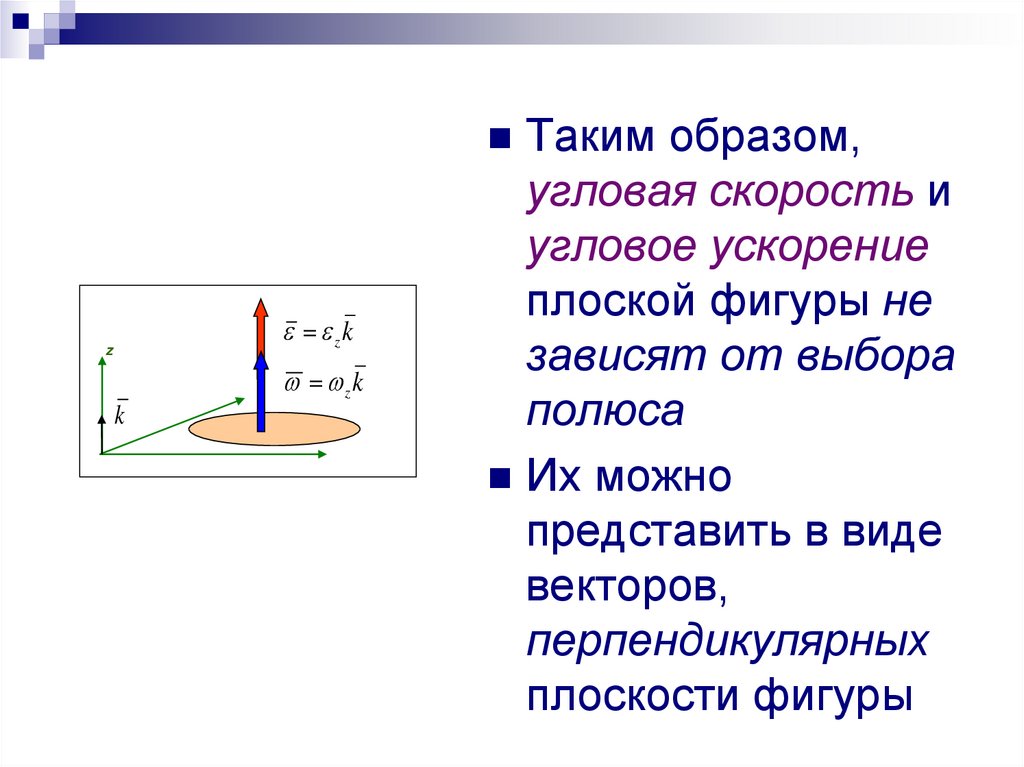
Таким образом,
zk
z
z k
k
угловая скорость и
угловое ускорение
плоской фигуры не
зависят от выбора
полюса
Их можно
представить в виде
векторов,
перпендикулярных
плоскости фигуры

16.

B
rAB
rB
rA
A
O
Теорема о сложении скоростей –
Скорость любой точки плоской
фигуры равна геометрической
сумме скоростей полюса и
вращательной скорости этой точки
вокруг полюса

17.

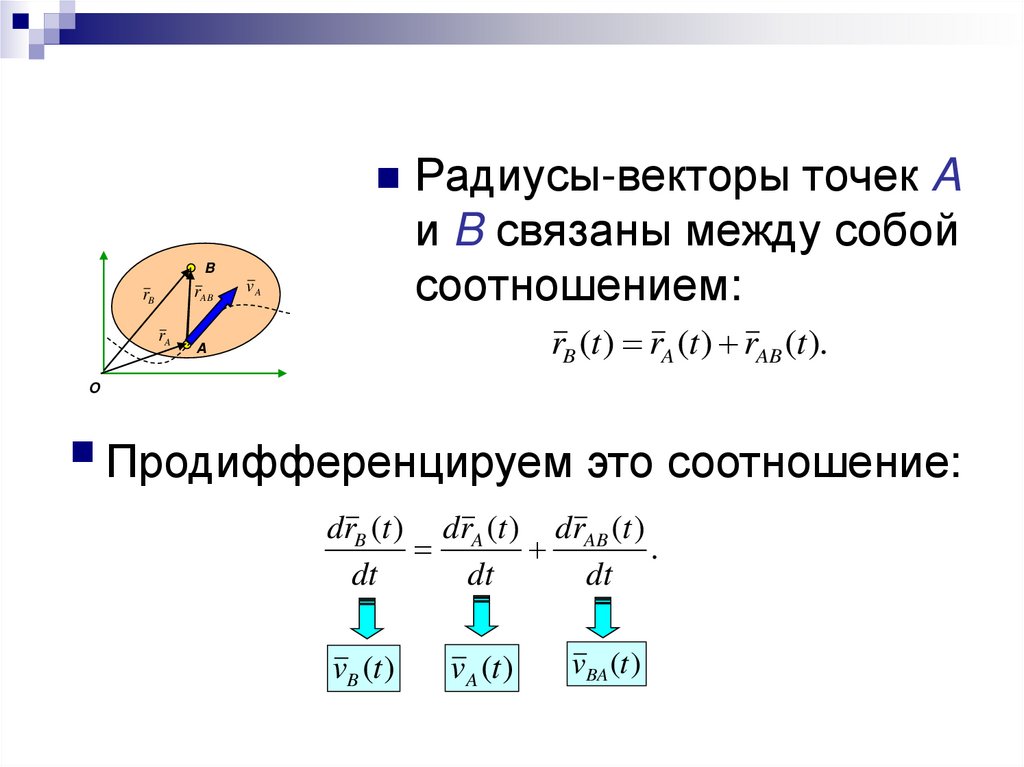
Радиусы-векторы точек A
и B связаны между собой
соотношением:
B
rAB
rB
rA
vA
rB (t ) rA (t ) rAB (t ).
A
O
Продифференцируем это соотношение:
drB (t ) drA (t ) drAB (t )
.
dt
dt
dt
vB (t )
v A (t )
vBA (t )

18.

Второе слагаемое есть
vB
vBA
B
vvAA
A
вращательная скорость
точки B вокруг полюса
A:
vBA (t ) (t ) rAB (t );
rAB const.
Таким образом, скорость точки B равна
геометрической сумме скорости полюса A и
вращательной скорости точки B вокруг
полюса:
vB vA rAB vA vBA.

19.

Следствие 1 – Проекции
vB
x1
vA
vBA
B
vA
A
скоростей точек
плоской фигуры на ось,
проходящую через эти
точки равны.
Спроецируем векторное соотношение
на ось x1:
( x1 ) :
vBx1 v Ax1 ,
(vBA x1 ).

20.

Следствие 2 – Концы
vCA c
vC
vBA b vB
A
C
B
vA
vA
vA
векторов скоростей
точек плоской фигуры,
лежащих на одной
прямой, также лежат на
одной прямой и делят
эту прямую на отрезки
пропорциональные
расстояниям между
точками.

21.

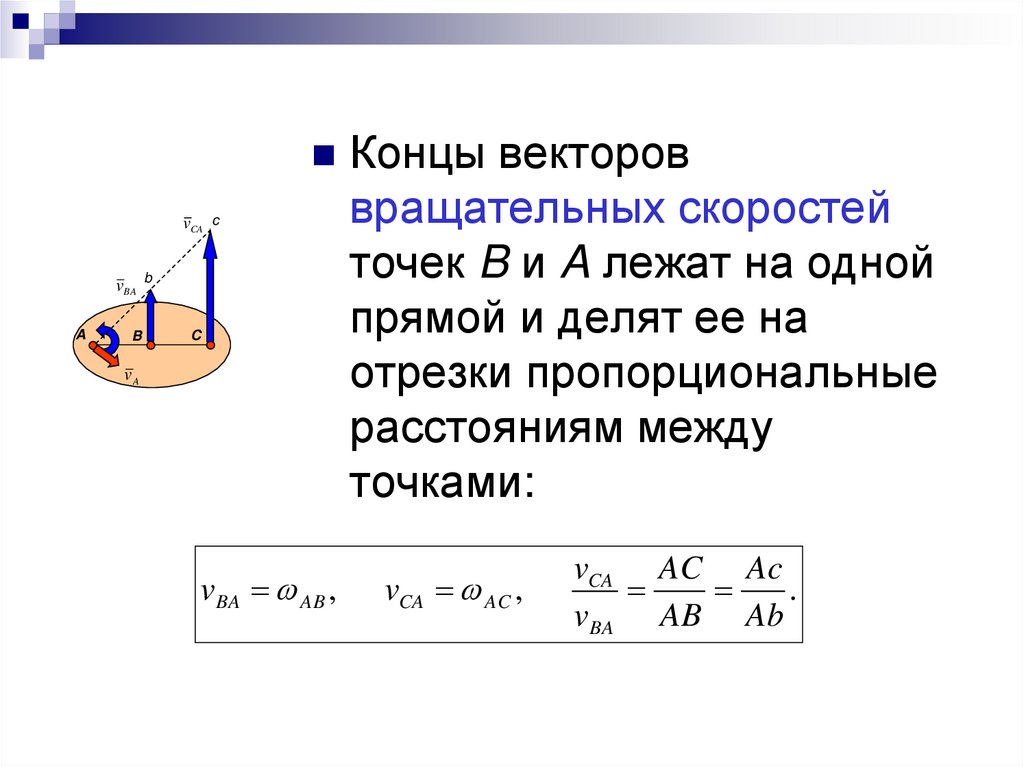
Концы векторов
vCA c
vBA b
A
B
C
vA
vBA AB ,
вращательных скоростей
точек B и A лежат на одной
прямой и делят ее на
отрезки пропорциональные
расстояниям между
точками:
vCA AC ,
vCA AC Ac
.
vBA AB Ab

22.

Концы векторов скоростей
vCA c
vC
vBA b vB
A
C
B
vA
vA
vA
полюса A лежат,
изображенных в точках B и C
также лежат на одной
прямой.
Нетрудно доказать из подобия
треугольников, что концы векторов
скоростей точек B и C также лежат на
одной прямой, и делят эту прямую на
части, пропорциональные расстояниям
между точками.

23.

Мгновенный центр скоростей (МЦС)
– При движении плоской фигуры в
каждый момент времени существует
точка, жестко связанная с плоской
фигурой, скорость которой в этот
момент равна нулю.

24.

Пусть известна скорость
P
A
vA
одной из точек фигуры и
угловая скорость вокруг этой
точки.
Запишем векторное
соотношение для скорости
некоторой точки P согласно
теоремы о сложении
скоростей:
vP vA rAP vA vPA.

25.

Зададим значение
vPA
P
vA
A
скорости этой точки P
равной нулю:
vA
vP 0.
Тогда получаем:
vPA rAP vA .

26.

vPA
P
vA
A
vA
Т.е. вращательная скорость искомой
точки должна быть равна по модулю
скорости точки A, параллельна этой
скорости и направлена в
противоположную сторону.

27.

Это позволяет найти
vPA
P
vA
A
vA
положение МЦС (точки P), а
именно: МЦС должен
находиться на
перпендикуляре к скорости
точки A, отложенном в
сторону угловой скорости, на
расстоянии:
AP
vA
.

28.

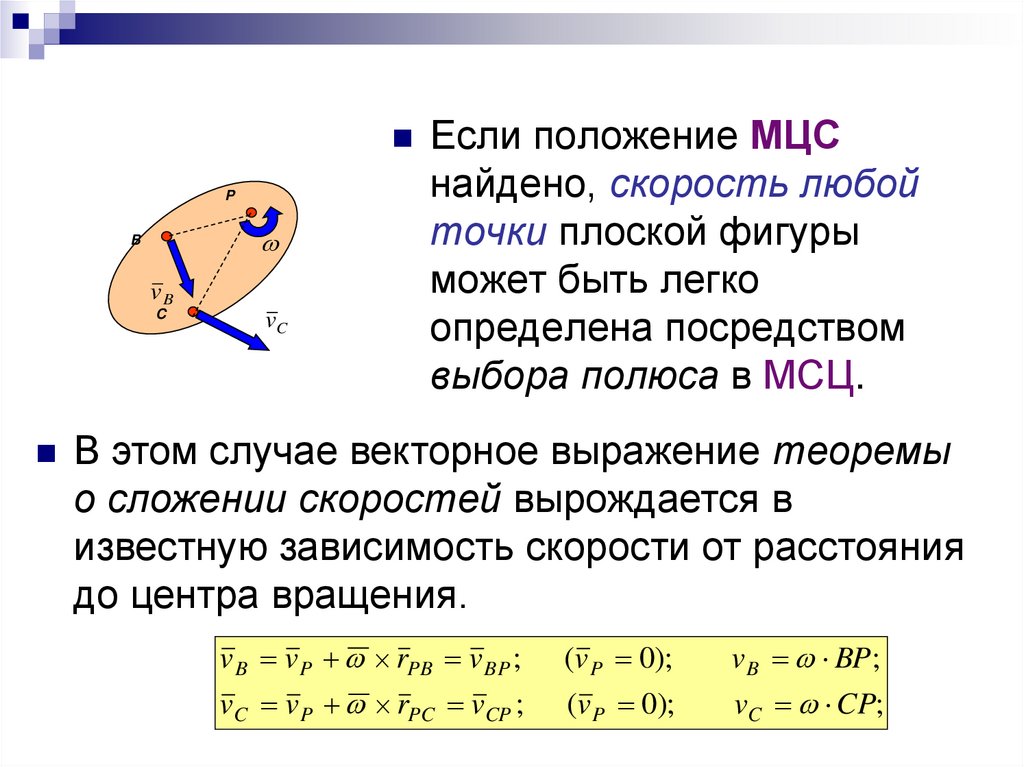
Если положение МЦС
P
B
vB
C
vC
найдено, скорость любой
точки плоской фигуры
может быть легко
определена посредством
выбора полюса в МСЦ.
В этом случае векторное выражение теоремы
о сложении скоростей вырождается в
известную зависимость скорости от расстояния
до центра вращения.
v B v P rPB v BP ;
(v P 0);
v B BP ;
vC v P rPC vCP ;
(v P 0);
vC CP;

29.

P
B
vB
C
vC
Другими словами, можно утверждать,
что в любой момент времени тело
не совершает никакого другого
движения, кроме как
вращательного движения вокруг
МЦС.

30. Спасибо за внимание!

Продолжение следует…