Similar presentations:
Плоскопараллельное движение твердого тела (тема 3)
1.
Плоскопараллельное движение твердого тела – движение при котором каждая точка тела движется в в плоскостипараллельной некоторой неподвижной плоскости. Сечение тела одной из таких плоскостей есть плоская фигура, остающаяся в этой
плоскости при движении тела.
Теорема о плоскопараллельном движении твердого тела – плоскопаралллельное
движение твердого тела однозначным образом определяется движением плоской
фигуры, образованной сечением тела одной из параллельных плоскостей.
M1
Выберем две точки на произвольных двух сечениях тела, находящиеся на одном перпендикуляре к
этим плоскостям:
M
M
Проведем
к каждой точке радиусы-векторы из неподвижной точки O и свяжем их между собой вектором
1
2
r1
M1M2:
r2 r1 M 1 M 2
M2
O
r2
При плоском движении тела вектор M1M2 не изменяется по величине, остается параллельным
самому себе (движется поступательно) и, следовательно, точки этого вектора описывают
тождественные траектории и имеют в каждый момент времени одинаковые скорости и ускорения:
dr2 dr1
d 2 r2 d 2 r1
; (M 1 M 2 const ); v2 v1 , и
2 ; a2 a1.
dt
dt
dt 2
dt
Таким образом, при плоском движении тела движение каждой точки одной из плоских фигур определяет движение соответствующих точек,
находящихся во всех других смежных параллельных плоскостях.
Следствие: Поскольку положение плоской фигуры однозначно определяется положением ее двух точек или отрезка прямой, проведенной
через эти точки, то плоскопараллельное движение твердого тела определяется движением прямолинейного отрезка,
принадлежащего одному из сечений тела параллельными плоскостями.
Разложение плоскопараллельного движения плоской фигуры на поступательное и вращательное движения – Плоскую фигуру
или отрезок прямой можно перевести из одного положения в другое бесчисленным множеством способов, меняя последовательность
выполнения поступательного и вращательного движения между собой, а также выбирая различные траектории и точки в качестве
полюса:
Таким образом, плоскопараллельное движение состоит из двух движений:
поступательное и вращательное, и его всегда можно разложить на эти два движения.
A1 y
При этом поступательное зависит от выбора полюса и траектории движения, а
Уравнение движения плоской фигуры: Выбирая в качестве полюса любую точку, например,
вращательное, характеризуемое поворотом вокруг выбранного полюса, не зависит от выбора
B
A, поступательная часть движения будет описываться уравнениями движения этой точки.
полюса (для любого полюса величина угла поворота и направление вращения – одинаковы).
Вращательная часть движения описывается уравнением изменения угла поворота вокруг
B
xC
A2
полюса:
Уравнения движения любой точки плоской фигуры, положение
yC
x A x A (t );
B2
A
xA
которой задается координатами локальной системы отсчета,
связанной с фигурой:
y
y
(
t
);
A
A
A
xC x A (t ) xC cos (t ) yC sin (t );
yA
(
t
).
x
10
yC y A (t ) xC sin (t ) yC cos (t ).
B1
2.
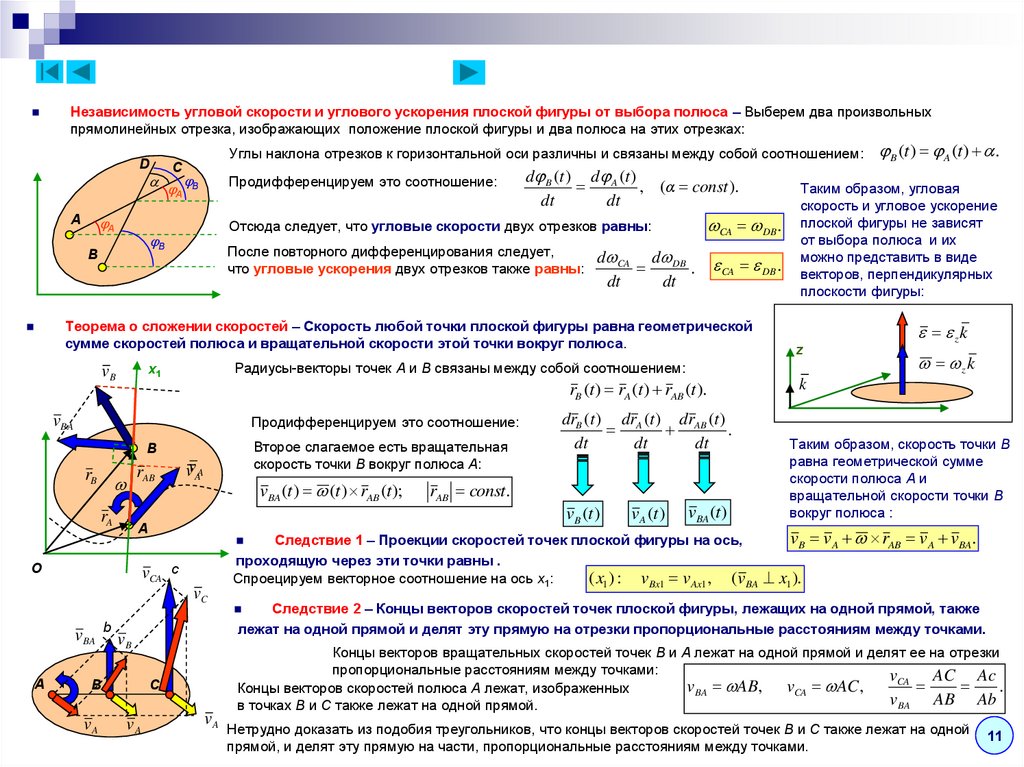
Независимость угловой скорости и углового ускорения плоской фигуры от выбора полюса – Выберем два произвольныхпрямолинейных отрезка, изображающих положение плоской фигуры и два полюса на этих отрезках:
D
A
A
С
A
Углы наклона отрезков к горизонтальной оси различны и связаны между собой соотношением:
B
Продифференцируем это соотношение:
После повторного дифференцирования следует,
d CA d DB
.
что угловые ускорения двух отрезков также равны:
dt
dt
CA DB .
Теорема о сложении скоростей – Скорость любой точки плоской фигуры равна геометрической
сумме скоростей полюса и вращательной скорости этой точки вокруг полюса.
rB (t ) rA (t ) rAB (t ).
vBA
Продифференцируем это соотношение:
Второе слагаемое есть вращательная
скорость точки B вокруг полюса A:
B
rB
rA
rAB
vvAA
vBA (t ) (t ) rAB (t );
vC
vBA b vB
vA
C
vA
rAB const.
vA
vA (t )
vBA (t )
Следствие 1 – Проекции скоростей точек плоской фигуры на ось,
проходящую через эти точки равны .
Спроецируем векторное соотношение на ось x1:
( x1 ) : vBx1 v Ax1 , (vBA
vCA c
B
drB (t ) drA (t ) drAB (t )
.
dt
dt
dt
vB (t )
A
O
Таким образом, угловая
скорость и угловое ускорение
плоской фигуры не зависят
от выбора полюса и их
можно представить в виде
векторов, перпендикулярных
плоскости фигуры:
zk
z
Радиусы-векторы точек A и B связаны между собой соотношением:
x1
vB
A
CA DB .
Отсюда следует, что угловые скорости двух отрезков равны:
B
B
d B (t ) d A (t )
, (α const ).
dt
dt
B (t ) A (t ) .
z k
k
Таким образом, скорость точки B
равна геометрической сумме
скорости полюса A и
вращательной скорости точки B
вокруг полюса :
vB vA rAB vA vBA.
x1 ).
Следствие 2 – Концы векторов скоростей точек плоской фигуры, лежащих на одной прямой, также
лежат на одной прямой и делят эту прямую на отрезки пропорциональные расстояниям между точками.
Концы векторов вращательных скоростей точек B и A лежат на одной прямой и делят ее на отрезки
пропорциональные расстояниям между точками:
vCA AC Ac
vBA AB, vCA AC ,
.
Концы векторов скоростей полюса A лежат, изображенных
vBA AB Ab
в точках B и C также лежат на одной прямой.
Нетрудно доказать из подобия треугольников, что концы векторов скоростей точек B и C также лежат на одной
прямой, и делят эту прямую на части, пропорциональные расстояниям между точками.
11
3.
Мгновенный центр скоростей (МЦС) – При движении плоской фигуры в каждый момент времени существует точка, жесткосвязанная с плоской фигурой, скорость которой в этот момент равна нулю.
Пусть известна скорость одной из точек фигуры и угловая скорость вокруг этой точки:
vPA
Запишем векторное соотношение для скорости некоторой точки P согласно теоремы о сложении скоростей:
vP vA rAP vA vPA. Зададим значение скорости этой точки P равной нулю: vP 0.
P
A
vA
vA
Тогда получаем:
vPA rAP vA . Т.е. вращательная скорость искомой точки должна быть равна по
модулю скорости точки A, параллельна этой скорости и направлена
в противоположную сторону.
Это позволяет найти положение МЦС (точки P), а именно: МЦС должен находиться на перпендикуляре к
скорости точки A, отложенном в сторону угловой скорости, на расстоянии:
AP
vA
.
Если положение МЦС найдено, скорость любой точки плоской фигуры может быть легко определена посредством выбора полюса в
МСЦ . В этом случае векторное выражение теоремы о сложении скоростей вырождается в известную зависимость скорости от
расстояния до центра вращения:
v B v P rPB v BP ;
(v P 0);
v B BP ;
vC v P rPC vCP ;
(v P 0);
vC CP;
Другими словами, можно утверждать, что в любой момент времени тело
не совершает никакого другого движения,
кроме как вращательного движения вокруг МЦС.
P
B
vB
C
vC
12
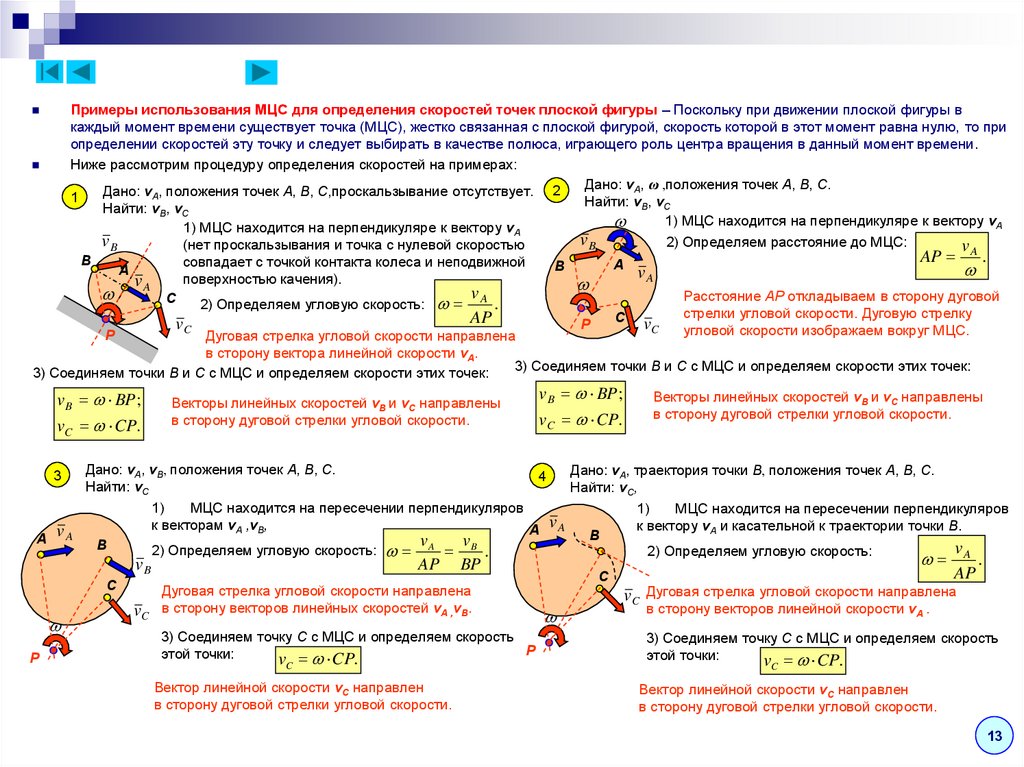
4.
Примеры использования МЦС для определения скоростей точек плоской фигуры – Поскольку при движении плоской фигуры вкаждый момент времени существует точка (МЦС), жестко связанная с плоской фигурой, скорость которой в этот момент равна нулю, то при
определении скоростей эту точку и следует выбирать в качестве полюса, играющего роль центра вращения в данный момент времени.
Ниже рассмотрим процедуру определения скоростей на примерах:
Дано: vA, ω ,положения точек A, B, C.
Дано: vA, положения точек A, B, C,проскальзывание отсутствует. 2
1
Найти: vB, vC
Найти: vB, vC
1) МЦС находится на перпендикуляре к вектору vA
1) МЦС находится на перпендикуляре к вектору vA
vB
vB
2) Определяем расстояние до МЦС:
(нет проскальзывания и точка с нулевой скоростью
v
AP A .
B
совпадает с точкой контакта колеса и неподвижной
A
B
A
vA
поверхностью качения).
vA
v
Расстояние AP откладываем в сторону дуговой
C
2) Определяем угловую скорость: A .
стрелки угловой скорости. Дуговую стрелку
C
AP
vC угловой скорости изображаем вокруг МЦС.
vC
P
P
Дуговая стрелка угловой скорости направлена
в сторону вектора линейной скорости vA.
3) Соединяем точки B и C с МЦС и определяем скорости этих точек:
v B BP ;
vC CP.
3) Соединяем точки B и C с МЦС и определяем скорости этих точек:
Векторы линейных скоростей vB и vC направлены
в сторону дуговой стрелки угловой скорости.
v B BP ;
vC CP.
Векторы линейных скоростей vB и vC направлены
в сторону дуговой стрелки угловой скорости.
Дано: vA, vB, положения точек A, B, C.
Дано: vA, траектория точки B, положения точек A, B, C.
4
Найти: vC
Найти: vC,
1)
МЦС находится на пересечении перпендикуляров
1)
МЦС находится на пересечении перпендикуляров
vA
к
векторам
v
,v
,
к
вектору
vA и касательной к траектории точки B.
A
B
A
v
B
A A
vA
vB
B
vA
2) Определяем угловую скорость:
2) Определяем угловую скорость:
.
3
vB
C
P
vC
AP
Дуговая стрелка угловой скорости направлена
в сторону векторов линейных скоростей vA ,vB.
3) Соединяем точку C с МЦС и определяем скорость
P
этой точки:
v CP.
C
Вектор линейной скорости vC направлен
в сторону дуговой стрелки угловой скорости.
BP
C
AP
.
vC Дуговая стрелка угловой скорости направлена
в сторону векторов линейной скорости vA .
3) Соединяем точку C с МЦС и определяем скорость
этой точки:
v CP.
C
Вектор линейной скорости vC направлен
в сторону дуговой стрелки угловой скорости.
13
5.
Примеры использования МЦС для определения скоростей точек плоской фигуры5
B vB
Дано: vA, vB, vA║vB, положения точек A, B, C.
Найти: vC
1) МЦС находится на пересечении перпендикуляров
A
v A к векторам vA и vB. Эта точка находится в бесконечности.
C
2) Угловая скорость обращается в нуль (мгновенно
поступательное движение):
vC
Дано: vA, vB, vA║vB, положения точек A, B, C.
Найти: vC
6
vC
3) Скорость точки C равна геометрически скоростям точек
A и B:
v v v .
C
A
B
Дано: vоA,сложении
vB, vA║vB, ускорений
положения точек
A, B, C. любой точки
7 Теорема
– Ускорение
Найти: vC
плоской фигуры равна геометрической сумме ускорения полюса
1) МЦС
находится
на пересечении перпендикуляров
и ускорения этой точки
вокруг
полюса.
к
векторам
v
и
v
.
Эти перпендикуляры сливаются
v
A
B
A
vCСкорости
точек
A и B связаны между собой соотношением:
A
в одну линию.
v
v
A
P
vC CP.
v2)
v A vBA положение
v A rAB
.
B
Определяем
МЦС
AB
Дуговую стрелку угловой скорости изображаем
в сторону векторов линейных скоростей vA ,vB.
3) Соединяем точку C с МЦС и определяем скорость этой точки:
Вектор скорости точки C направлен параллельно векторам
скоростей точек A и B (в ту же сторону).
vB
B
C
v A vB
0.
1) МЦС находится на пересечении перпендикуляров
к векторам vA и vB. Эти перпендикуляры сливаются
в одну линию.
v
v
2) Определяем положение МЦС A B
AP BP
(проводим линию через концы
векторов vA и vB) и угловую
v vB
A
.
скорость:
vA
A
B
AP BP
(проводим
линию через
концы
CПродифференцируем
это соотношение
по времени:
P
v vB
векторов vA и vB) и угловую
A
.
d
v
d
v
d
v
d
B
B
A
AB
vB
скорость:
BA a A ( rAB ).
dt Дуговую
dt
dt
dt скорости изображаем
стрелку угловой
в сторону векторов
линейных скоростей
vA ,vB.
Второе слагаемое дифференцируем
как произведение
двух функций:
3) Соединяем
точку Cd
с МЦС и определяем
скорость этой точки:
dr
d
( rAB )
rAB AB rAB v BA .
Вектор линейнойdt
скорости vC направлен
dt
vC CP. dt
в сторону дуговой стрелки угловой скорости.
Получили сумму вращательного и осестремительного ускорений
рассматриваемой точки относительно полюса. Таким образом,
Пример
использования
МЦС при исследовании работы
ускорение
точки
плоской фигуры:
кривошипно-шатунного механизма – См. решение задачи М.16.28
вр
ос
“Теоретическая механика
и задачах.
Кинематика” (электронное
aB вaпримерах
A a BA a BA a A a BA .
пособие автора www.miit.ru/institut/ipss/faculties/trm/main.htm ),
Вектор линейной скорости vC направлен
в сторону дуговой стрелки угловой скорости.
Следствие – Концы векторов ускорений точек плоской
фигуры, лежащих на одной прямой, также лежат на одной
прямой и делят ее на отрезки, пропорциональные расстояниям
между точками.
Концы векторов ускорений точек aBA и aСA
aCA b
лежат на одной прямой Abc и делят ее на
aC отрезки пропорциональные расстояниям
между точками:
a BA a
a 2 4 AB,
BA
A
aCA 2 4 AC.
aB
C
B
aA
aA
aA
Концы векторов ускорений полюса A,
изображенных в точках B и C, лежат
также лежат на одной прямой.
Нетрудно доказать из подобия треугольников, что концы векторов
суммарных ускорений точек B и C также лежат на одной прямой,
и делят эту прямую на части, пропорциональные расстояниям
между точками.
14
6.
Мгновенный центр ускорений (МЦУ) – При движении плоской фигуры в каждый момент времени существует точка, жесткосвязанная с плоской фигурой, ускорение которого в этот момент равна нулю.
a PA
A
Пусть известно ускорение одной из точек фигуры, угловая скорость и угловое ускорение вокруг этой точки:
Q
aA
Запишем векторное соотношение для ускорения некоторой точки Q согласно теоремы о сложении ускорений:
aQ a A rAQ vQA a A a PA .
Тогда получаем:
aA
Угол между вектором полного ускорения точки
при вращении относительно центра равен:
aQA a A .
arctg
a Q 0.
Зададим значение ускорения этой точки Q равной нулю:
.
2
Т.е. ускорение искомой точки при вращении вокруг полюса должно
быть равно по модулю ускорению точки A, параллельно этому
ускорению и направлено в противоположную сторону.
a
A
Это позволяет найти положение МЦУ (точки Q), а именно: МЦУ должен находиться прямой, составляющей AQ
.
2
угол к вектору ускорения точки A, проведенной в сторону углового ускорения, на расстоянии:
4
Если положение МЦУ найдено, ускорение любой точки плоской фигуры может быть легко определено посредством выбора полюса в
МСУ . В этом случае векторное выражение теоремы о сложении ускорений вырождается в известную зависимость полного ускорения от
расстояния до центра вращения:
2
4
aB aQ rQB vBQ aBQ ;
(aQ 0);
aB BQ ;
aC aQ rQC vCQ aCQ ;
(aQ 0);
aC 2 4 CQ;
Таким образом, при определении ускорений точек плоской фигуры в данный момент времени
можно считать, что тело совершает вращательное движение вокруг МЦУ.
Внимание: На самом деле в данный момент тело вращается вокруг МЦС,
положение которого в общем случае не совпадает с положением МЦУ.
Примеры использования МЦУ для определения ускорений точек плоской фигуры
1
Дано: aA, , , положения точек A, B.
Найти: aB
arctg
1)
МЦУ
находится
на
прямой
,
составляющей
угол
2
к вектору ускорения точки A, проведенной в сторону
углового ускорения, на расстоянии:
aA
Q
AQ
.
2
4
A
2) Соединяем точку B с МЦУ
aA
aB и определяем ускорение этой точки:
B
a 2 4 QB.
B
Q
B
aB
aC
C
a
.
A
Если = 0 и 0, то = 0 и AQ 2 .
Ускорения всех точек
будут направлены в точку Q (МЦУ).
a
Если 0 и = 0, то = 90о и AQ A .
Ускорения всех точек
будут перпендикулярны отрезкам, соединяющим
точки с МЦУ, и направлены в сторону углового
ускорения.
15
7.
Примеры использования МЦУ для определения ускорений точек плоской фигурыДано: aA, aB, положения точек A, B, C.
Использование МЦУ связано с геометрическим построениями и
Найти: aC
решениями косоугольных треугольников, что не совсем удобно
1) Запишем теорему о сложении ускорений
в общем случае. Можно решить эту задачу алгебраически
и найдем ускорение точки B во вращении вокруг
aA A
с помощью проекций:
полюса A:
a
a
a
.
1) Запишем теорему о сложении
B
A
BA
B
y
a
ускорений для точек B и A:
a
C
A
A
2) Определим угол между вектором aBA и прямой
C
вр
ос
B
AB и направление дуговой стрелки углового ускорения:
a BA
a B a A a BA
a BA
.
ос
ос
a
a
BA
CA
3) МЦУ находится на пересечении прямых, повернутых
aB
и изобразим компоненты ускорений:
C
на угол от векторов ускорений точек A и B в сторону
Q
вр 2) Спроецируем уравнение на
вр
aCA
дуговой стрелки углового ускорения:
a B a BA
координатные оси:
x
4) Соединяем точку C с МЦУ и определяем ускорение
этой точки из одного из соотношений:
вр
вр
ос
ос
a
aA
a
a Bx a Ax a BAx
a BAx
a Ax AB cos( a BA
, x) 2 AB cos( a BA
, x),
и направляем вектор ускорения под
B C .
вр
вр
ос
ос
AQ BQ CQ
углом к отрезку QC в сторону
a By a Ay a BAy
a BAy
a Ay AB cos( a BA
, y ) 2 AB cos( a BA
, y ).
дуговой стрелки углового ускорения.
3) Из этих уравнений можно найти угловые скорость и ускорение.
2
aA
4) Запишем теорему о сложении ускорений для точек С и A:
вр
и изобразим компоненты ускорений:
aC a A aCA
5) Спроецируем уравнение на
координатные оси:
ос
aCA
.
вр
вр
ос
ос
aCx aCx aCAx
aCAx
aCx AC cos( aCA
, x) 2 AC cos( aCA
, x),
вр
вр
ос
ос
aCy aCy aCAy
aCAy
aCy AC cos( aCA
, y ) 2 AC cos( aCA
, y ).
Пример решения – См. задачу М.18.13 “Теоретическая механика
в примерах и задачах. Кинематика” (электронное пособие автора
www.miit.ru/institut/ipss/faculties/trm/main.htm ),
16





 physics
physics








