Кинематика твердого тела. Простейшие движения твердого тела

1. Простейшие движения твердого тела

Кинематика
Кинематика твердого
твердого тела
тела
Простейшие движения твердого тела
• Поступательное движение
• Вращение вокруг неподвижной оси
(вращательное)

2.

Поступательное
Поступательное движение
движение
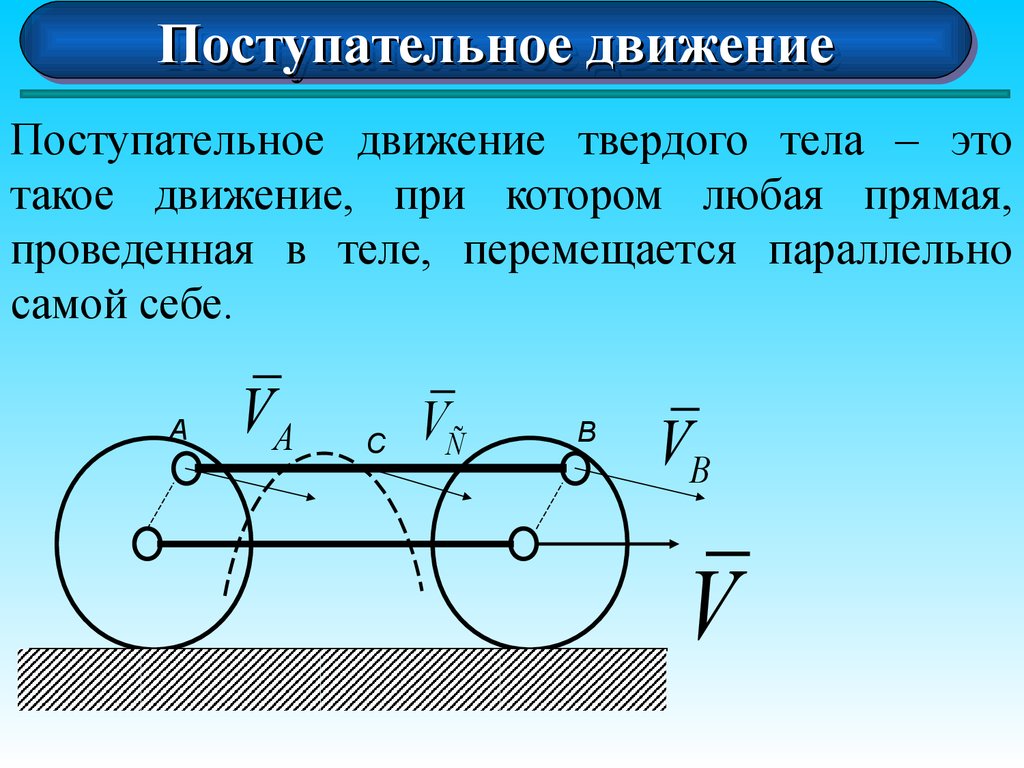
Поступательное движение твердого тела – это
такое движение, при котором любая прямая,
проведенная в теле, перемещается параллельно
самой себе.
А
VA
С
VÑ
В
VB
V

3.

Поступательное
Поступательное движение
движение
VA = Vc = VB
a A = aC = aB
При поступательном движении все точки тела
описывают одинаковые траектории и имеют в
каждый момент времени одинаковые по модулю и
направлению скорости и ускорения.

4.

Вращательное
Вращательное движение
движение
Вращательное движение твердого тела
• Вращательное движение твердого тела – это
такое движение, при котором две точки тела
остаются неподвижными.
• Проходящая через эти точки прямая называется
осью вращения.

5. Закон вращательного движения:

Вращательное
Вращательное движение
движение
Положение тела при вращательном движении
однозначно определяется углом поворота φ
Закон вращательного движения:
j = j(t )

6.

Вращательное
Вращательное движение
движение
•Основные кинематические характеристики
вращательного движения:
Угловая скорость ω
[рад/c]
Угловое ускорение ε [рад/c2]
Z
z
z

7.

Вращательное
Вращательное движение
движение
dj
=
= j&
dt
d
&= j
&
&
=
=
dt
Вектор угловой скорости лежит на оси вращения и
направлен в сторону, откуда видно, что тело
вращается против хода часовой стрелки.

8.

Вращательное
Вращательное движение
движение
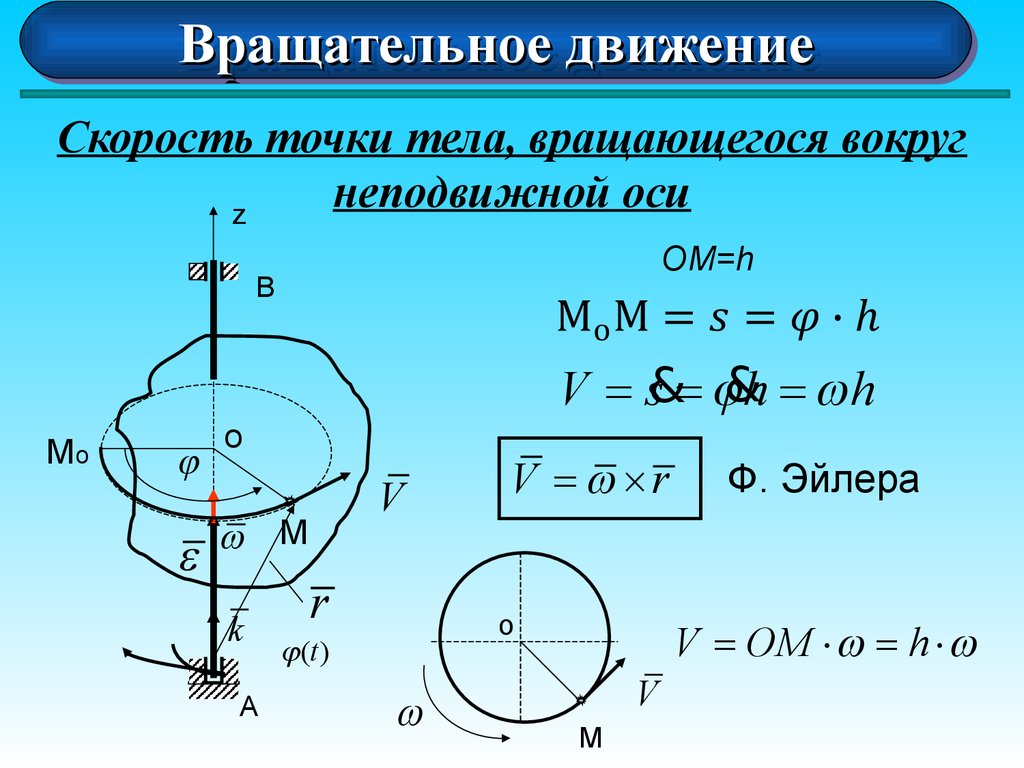
Скорость точки тела, вращающегося вокруг
неподвижной оси
z
ОМ=h
B
V = s&= j&h = h
Мо
j
о
V
М
k
A
r
V = ´r
о
j (t )
Ф. Эйлера
V = OM × = h ×
V
М

9.

Вращательное
Вращательное движение
движение
Ускорение точки тела, вращающегося вокруг
неподвижной оси
a = at + an
at = V&
t = R
a
О
R
R)
(
V
an =
=
= 2 × R
R
R
2
2
at
an
М
V
a = a +a = R +
2
n
2
t
4
2

10.

Преобразование
Преобразование вращательного
вращательного движения
движения
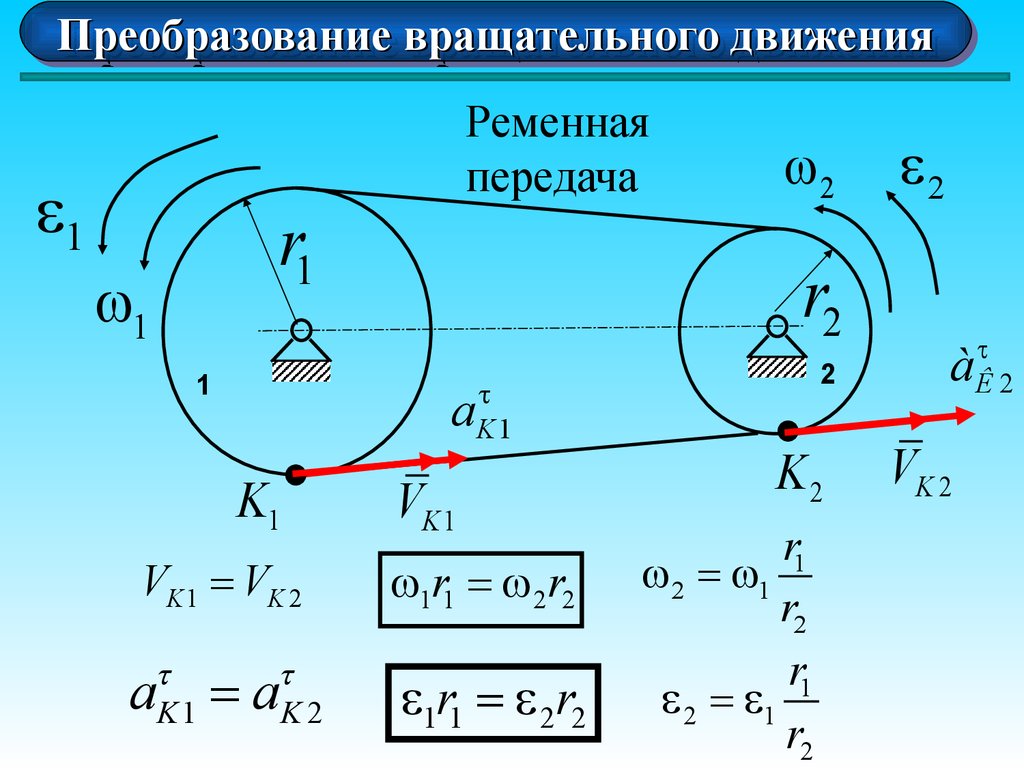
1
Ременная
передача
r1
1
1
VK 1 = VK 2
t
K1
r2
a
K1
t
K2
a =a
2
t
K1
VK 1
1r1 = 2 r2
1r1 = 2 r2
2
K2
r1
2 = 1
r2
r1
2 = 1
r2
2
àÊt 2
VK 2

11.

Преобразование
Преобразование вращательного
вращательного движения
движения
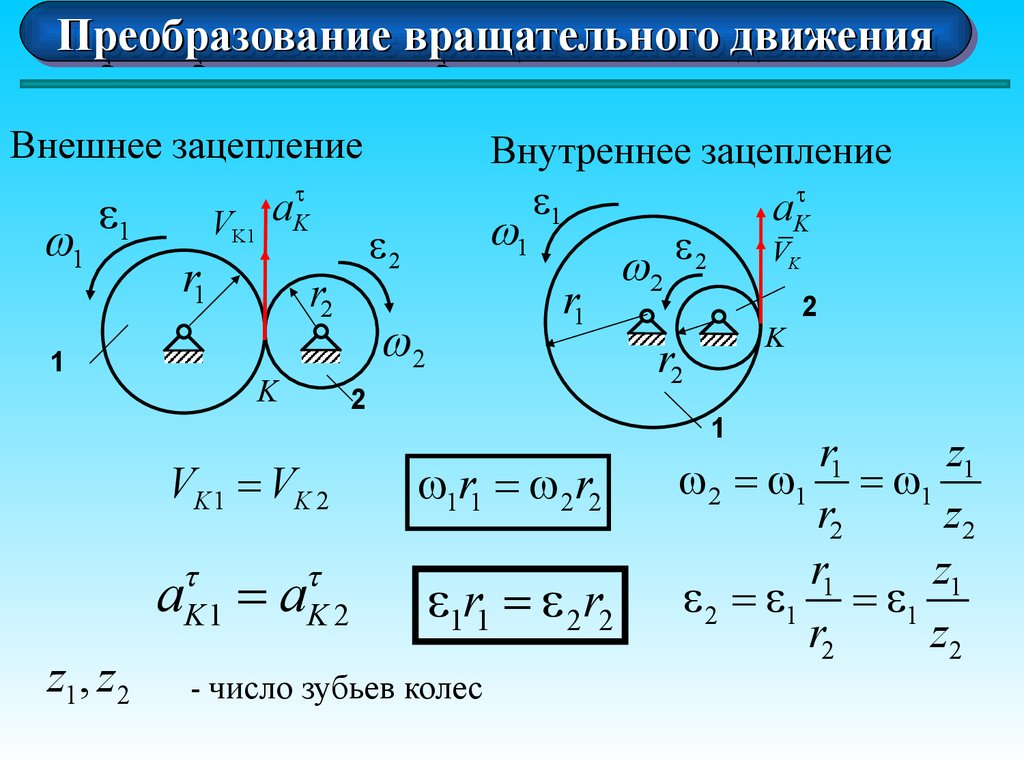
Внешнее зацепление
1
t
a
VK1 K
1
r1
1
2
2
VK 1 = VK 2
1
1r1 = 2 r2
t
K1
t
K2
- число
зубьев колес
a =a
z1 , z2
2
r2
K
Внутреннее зацепление
1
aKt
1
2
VK
2
r1
2
K
r2
1r1 = 2 r2
r1
z1
2 = 1 = 1
r2
z2
r1
z1
2 = 1 = 1
r2
z2

12.

Сложное
Сложное движение
движение точки
точки
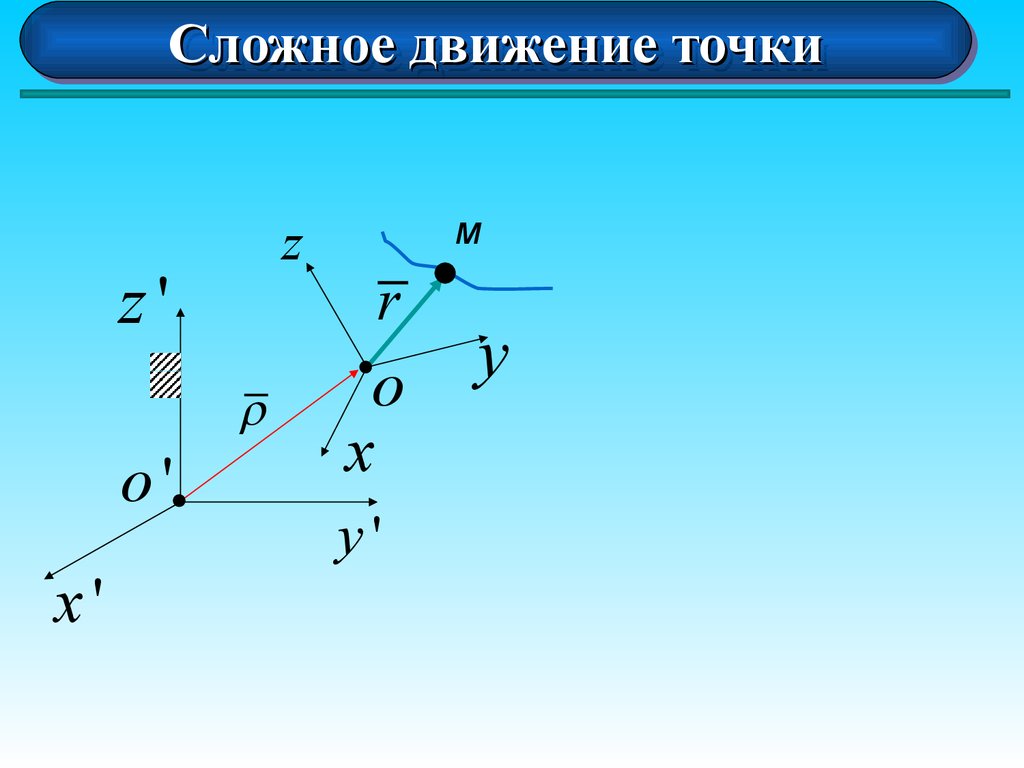
Сложное движение точки
Сложное движение точки - такое движение,
которое может быть составлено из двух
(нескольких) простых.
Движение рассматривается в двух системах
отсчета: основной (неподвижной) и движущейся.

13.

Сложное
Сложное движение
движение точки
точки
z
z'
r
o'
x'
м
r
o
x
y'
y

14.

Сложное
Сложное движение
движение точки
точки
Движение
точки
относительно
основной
(неподвижной) системы отсчета называется
абсолютным.
Движение точки относительно подвижной
системы отсчета называется относительным.
Движение подвижной системы отсчета (и
неизменно связанных с ней точек пространства)
называется переносным.

15. Абсолютная скорость точки - скорость относительно неподвижной системы отсчета. Относительная скорость точки - скорость относительно подв

Сложное
Сложное движение
движение точки
точки
Абсолютная скорость точки - скорость
относительно неподвижной системы отсчета.
Относительная скорость точки - скорость
относительно подвижной системы отсчета
Скорость неизменно связанной с подвижными
осями точки, с которой в данный момент
совпадает
движущаяся
точка,
называется
переносной скоростью.

16. Теорема о сложении скоростей:

Сложное
Сложное движение
движение точки
точки
Теорема о сложении скоростей:
V = Vотн + Vпер
Абсолютная скорость точки равна геометрической
сумме переносной и относительной скоростей

17.

Сложное
Сложное движение
движение точки
точки
Скорости и ускорения при сложном движении
обозначаются
Va ,
aa - абсолютные
Vr ,
ar - относительные
Ve ,
ae - переносные
Сложение векторов скорости по теореме косинусов
Va
Ve
j
Vr
Va = Vr + Ve
Va = Vr2 + Ve2 + 2VrVe cos j

18. Теорема Кориолиса

Сложное
Сложное движение
движение точки
точки
Теорема Кориолиса
a = aотн + апер + аКор
Абсолютное
ускорение
точки
равно
геометрической сумме переносного ускорения,
относительного ускорения и ускорения Кориолиса

19.

Сложное
Сложное движение
движение точки
точки
Ускорение Кориолиса характеризует изменение
относительной скорости точки в переносном
движении и переносной скорости точки в
относительном движении.
Кориолисово ускорение равно удвоенному
векторному произведению переносной угловой
скорости на относительную скорость точки
aКор = 2 пер ´ Vотн

20.

Сложное
Сложное движение
движение точки
точки
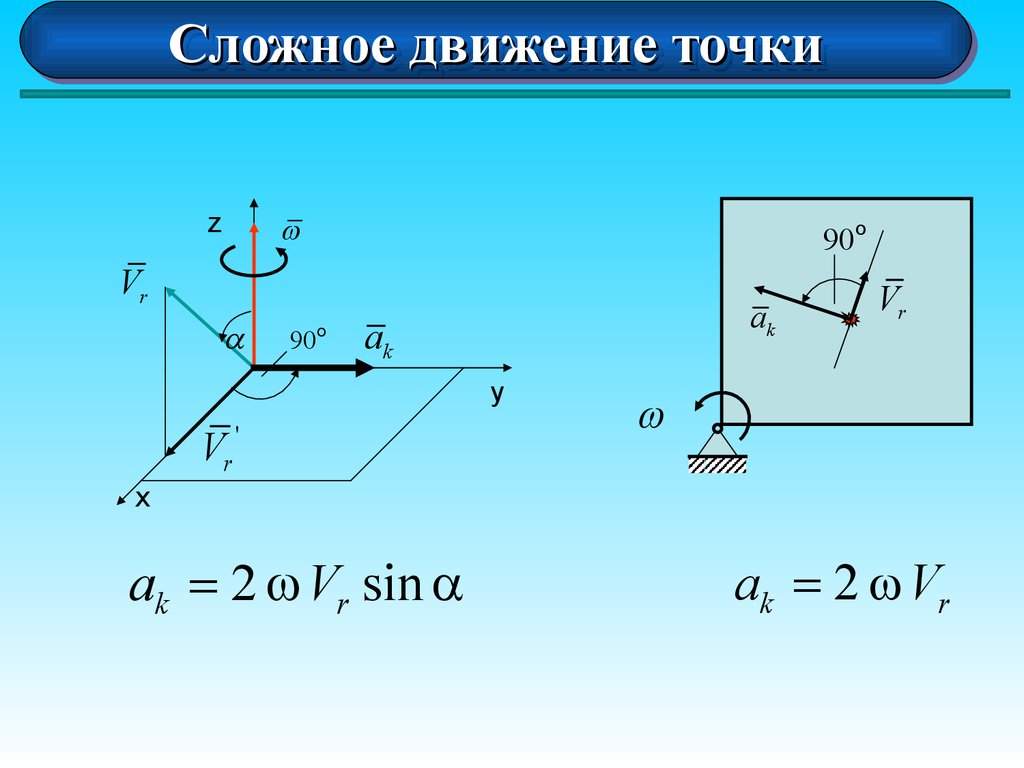
В численном виде, ускорение кориолиса равно
ak = 2 Vr sin( ^ Vr )
Правило Н. Е. Жуковского
Чтобы найти направление вектора ускорения
Кориолиса, необходимо спроецировать вектор
относительной
скорости
на
плоскость,
перпендикулярную , и повернуть эту проекцию
на 90 в сторону переносного вращения.

21.

Сложное
Сложное движение
движение точки
точки
z
90o
Vr
a
90o
ak
ak
y
Vr
'
Vr
x
ak = 2 Vr sin a
ak = 2 Vr

22.

Сложное
Сложное движение
движение точки
точки
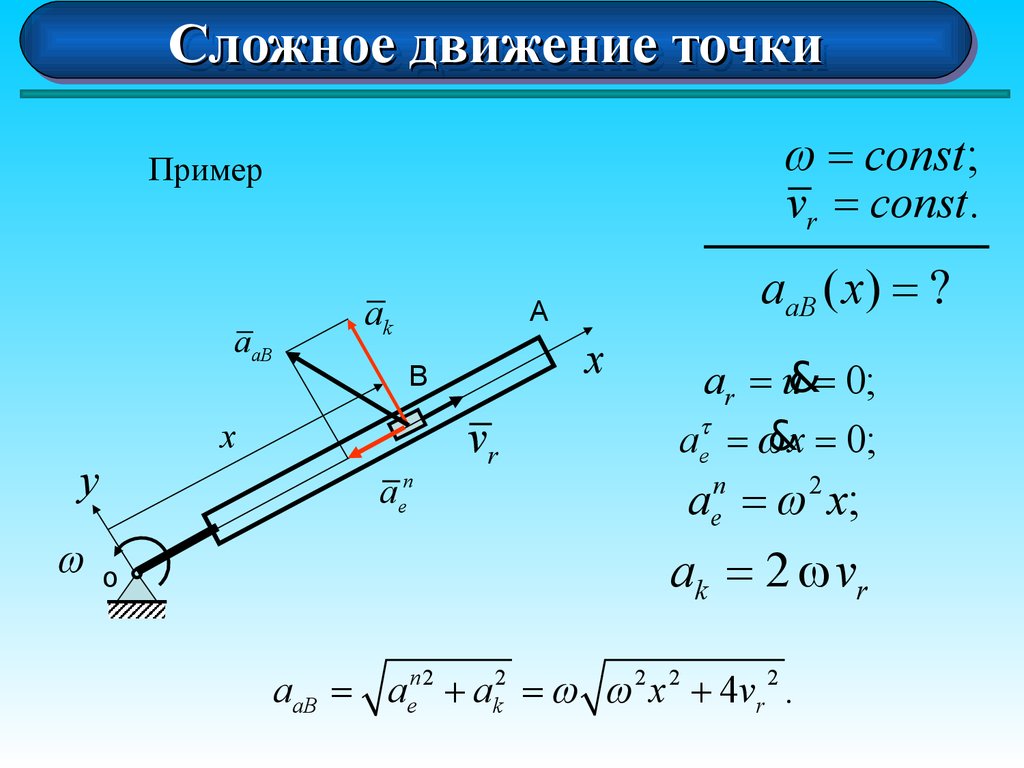
= const ;
Пример
aaB
ak
x
В
vr
aen
о
aaB ( x) = ?
А
x
y
vr = const.
ar = u&= 0;
aet = &x = 0;
a = x;
n
e
2
ak = 2 vr
aaB = aen 2 + ak2 = 2 x 2 + 4vr 2 .

23.

Плоское
Плоское движение
движение твердого
твердого тела
тела
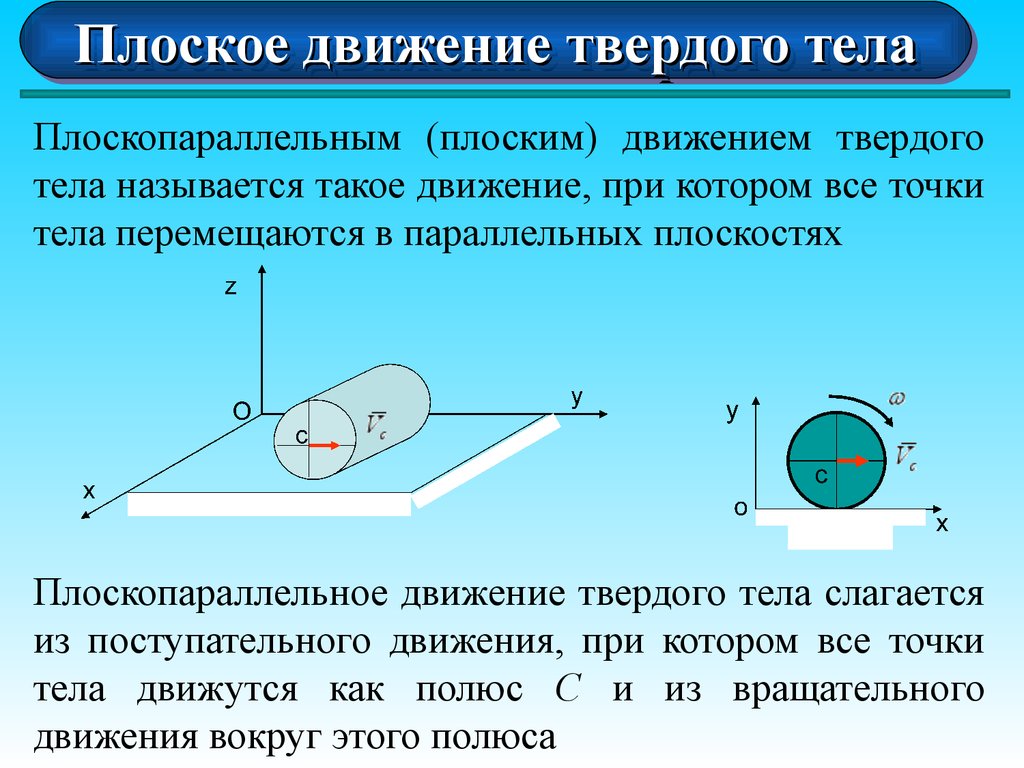
Плоскопараллельным (плоским) движением твердого
тела называется такое движение, при котором все точки
тела перемещаются в параллельных плоскостях
Плоскопараллельное движение твердого тела слагается
из поступательного движения, при котором все точки
тела движутся как полюс С и из вращательного
движения вокруг этого полюса

24.

Плоское
Плоское движение
движение твердого
твердого тела
тела
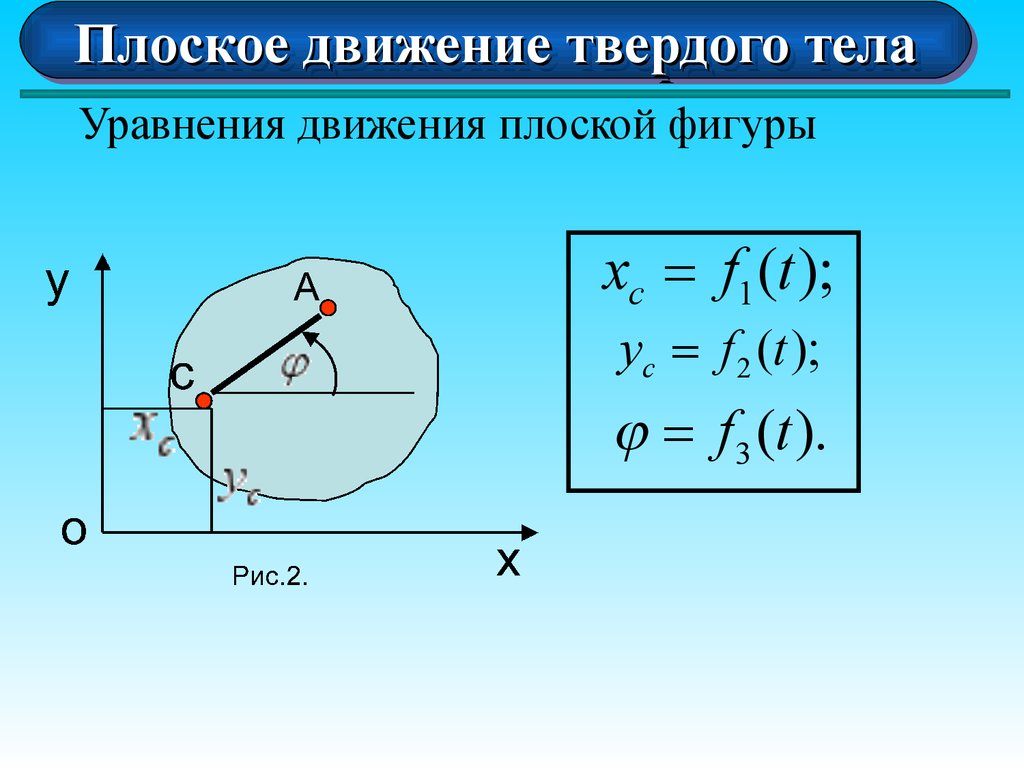
Уравнения движения плоской фигуры
xc = f1 (t );
yc = f 2 (t );
j = f3 (t ).

25.

Плоское
Плоское движение
движение твердого
твердого тела
тела
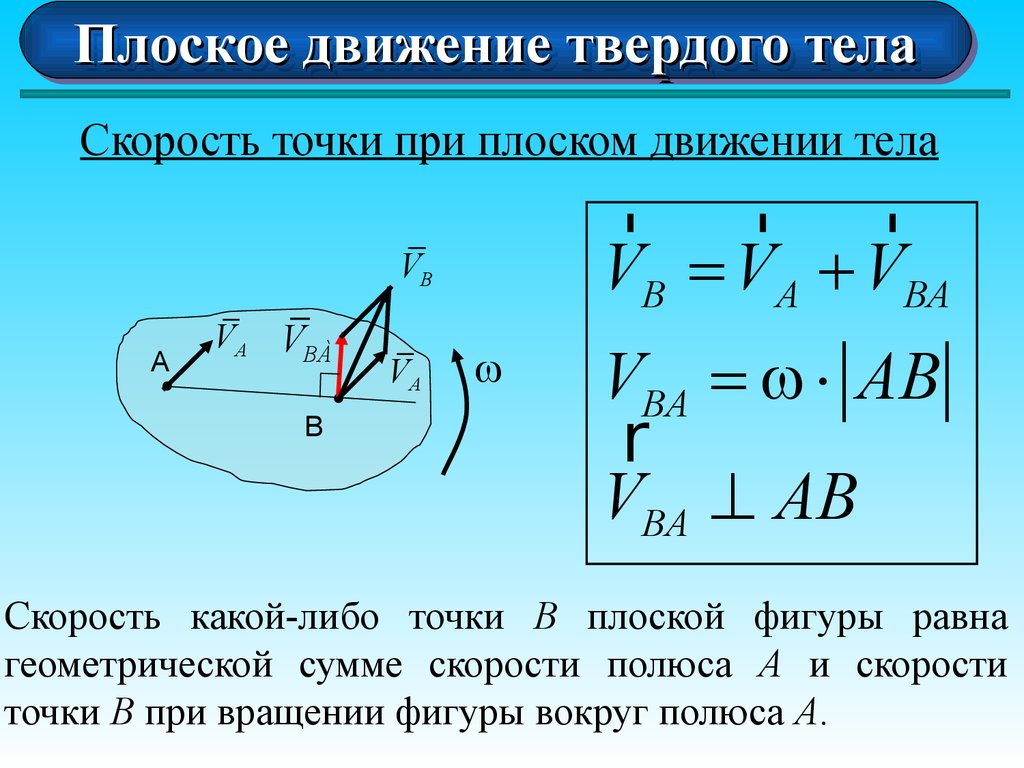
Скорость точки при плоском движении тела
r
r r
VB = VA + VBA
VB
А
VA VBÀ
В
VA
VBA = × AB
r
VBA ^ AB
Скорость какой-либо точки В плоской фигуры равна
геометрической сумме скорости полюса А и скорости
точки В при вращении фигуры вокруг полюса А.

26.

Плоское
Плоское движение
движение твердого
твердого тела
тела
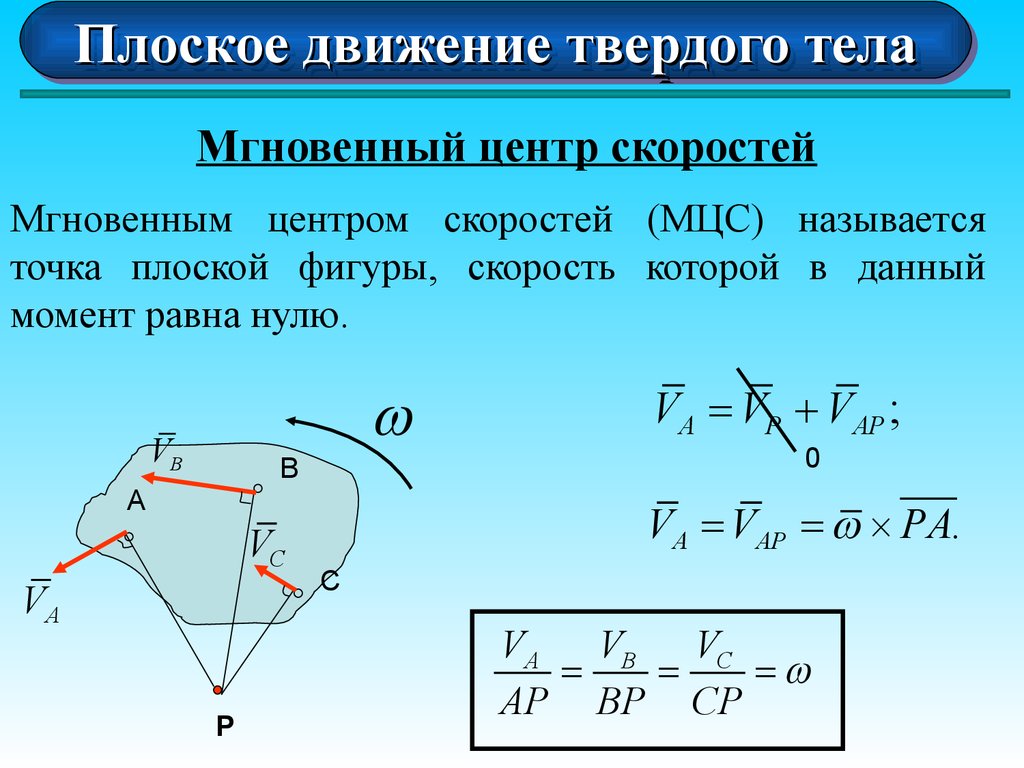
Мгновенный центр скоростей
Мгновенным центром скоростей (МЦС) называется
точка плоской фигуры, скорость которой в данный
момент равна нулю.
VB
B
A
VC
VA
P
VA = VP + VAP ;
0
VA = VAP = ´ PA.
C
VA VB VC
=
=
=
AP BP CP

27.

Плоское
Плоское движение
движение твердого
твердого тела
тела
Свойства МЦС:
•Скорости всех точек фигуры перпендикулярны отрезкам,
соединяющим эти точки с МЦС
•Модули скоростей пропорциональны расстояниям точек
до МЦС
•Угловая скорость тела равна в каждый данный момент
времени отношению скорости какой-нибудь точки к ее
расстоянию до МЦС

28.

Плоское
Плоское движение
движение твердого
твердого тела
тела
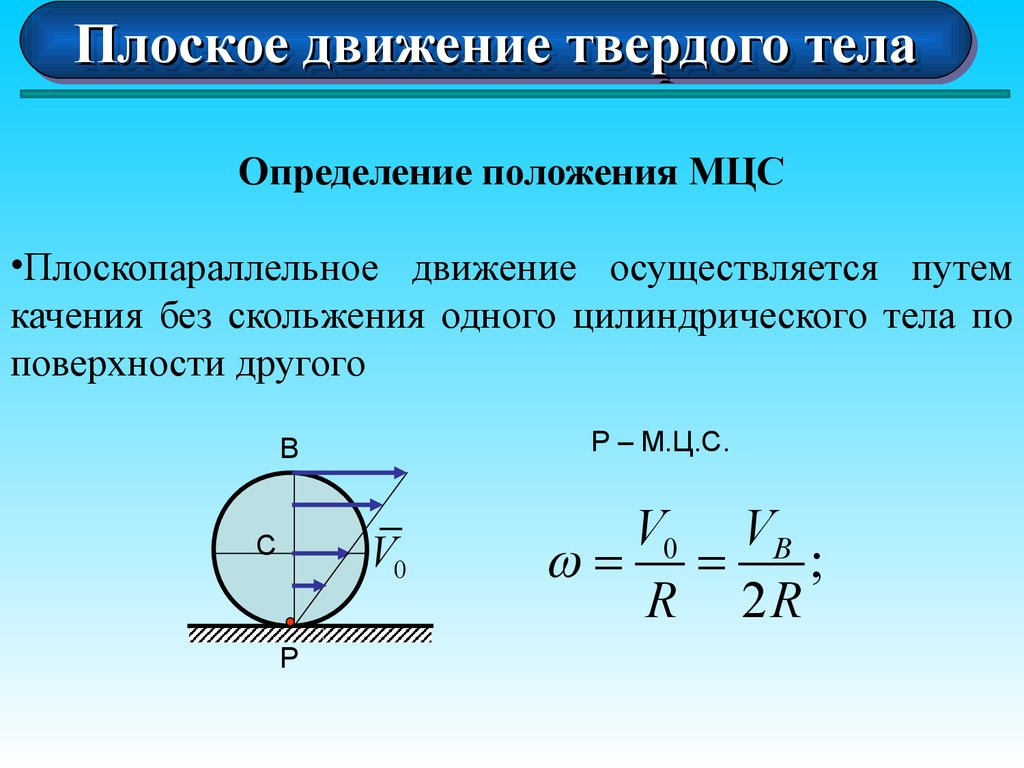
Определение положения МЦС
•Плоскопараллельное движение осуществляется путем
качения без скольжения одного цилиндрического тела по
поверхности другого
P – M.Ц.С.
B
V0
C
P
V0 VB
= =
;
R 2R

29.

Плоское
Плоское движение
движение твердого
твердого тела
тела
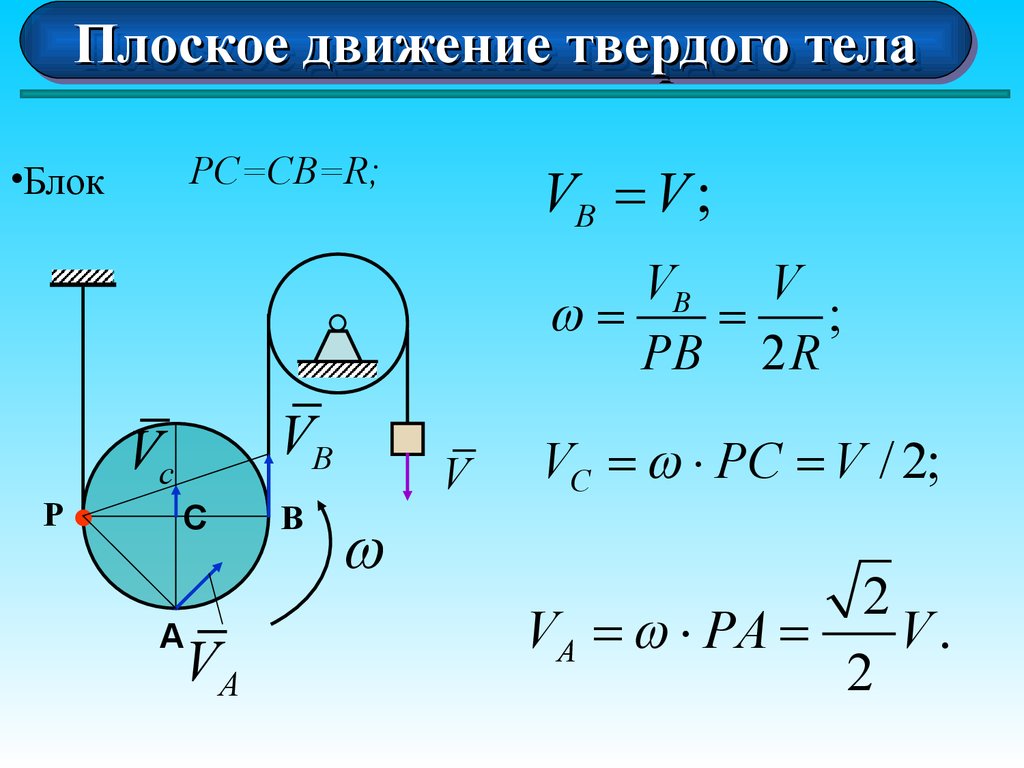
PC=CB=R;
•Блок
VB = V ;
VB
V
=
=
;
PB 2 R
VB
Vc
P
С
A
VA
B
V
VC = × PC = V / 2;
2
VA = × PA =
V.
2

30.

Плоское
Плоское движение
движение твердого
твердого тела
тела
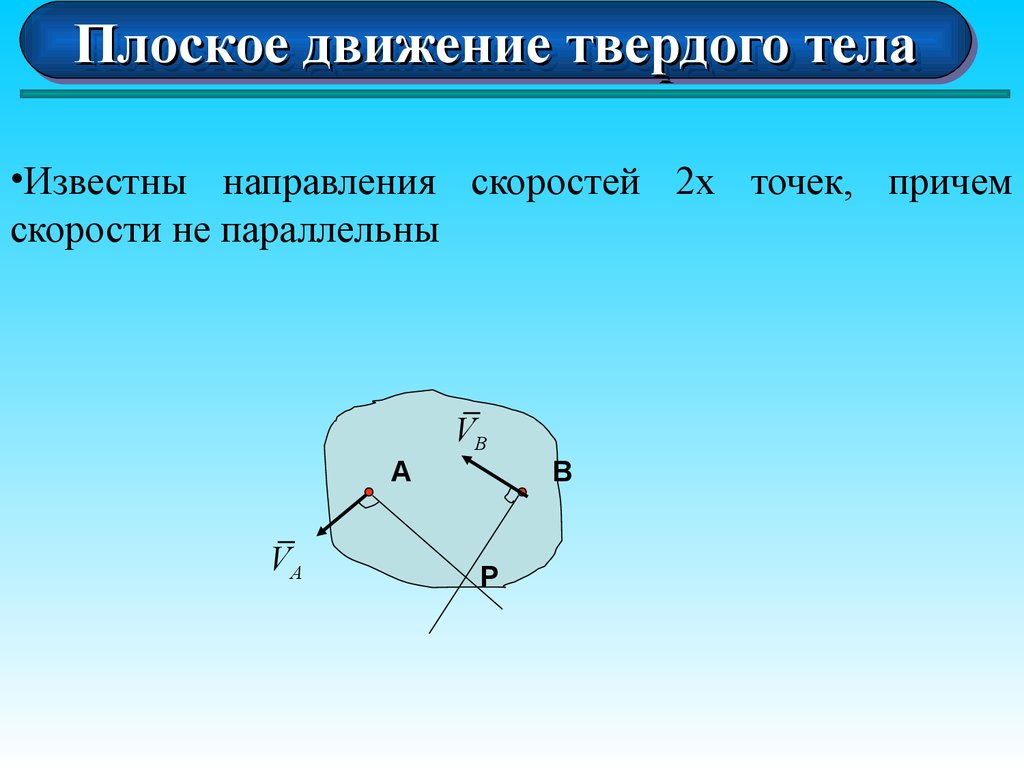
•Известны направления скоростей 2х точек, причем
скорости не параллельны
VB
А
VA
В
Р

31.

Плоское
Плоское движение
движение твердого
твердого тела
тела
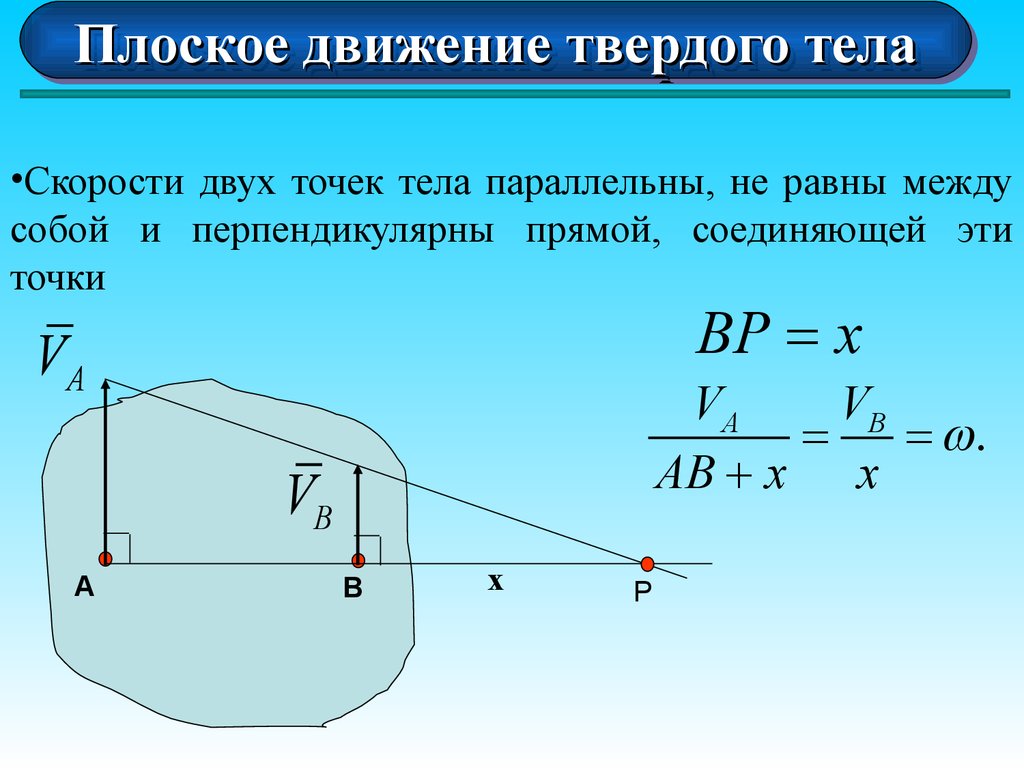
•Скорости двух точек тела параллельны, не равны между
собой и перпендикулярны прямой, соединяющей эти
точки
BP = x
VA
VA
VB
=
= .
AB + x x
VB
А
В
х
Р