Кинематика твердого тела. Простейшие движения твердого тела

1. МЕХАНИКА

Механическое движение,
виды движения и его
характеристики.

2. МЕХАНИКА

Наука об общих законах
движения тел.
ЗАДАЧА МЕХАНИКИ
Основной задачей механики
является определение
положения тела в любой
момент времени.

3. Механическое движение

Перемещение тела в
пространстве относительно
других тел с течением времени.

4. Разделы классической механики:

Статика изучает законы
равновесия системы тел.
Кинематика рассматривает
описание движения тел.
Динамика изучает влияние
взаимодействий между телами на
их механическое движение.

5. Основные понятия кинематики:

1.Материальная точка
2.Система отсчета
3.Перемещение
4.Траектория
5.Путь
6.Скорость

6. Материальная точка

Тело, размерами которого в
данных условиях можно
пренебречь, называют
материальной точкой.

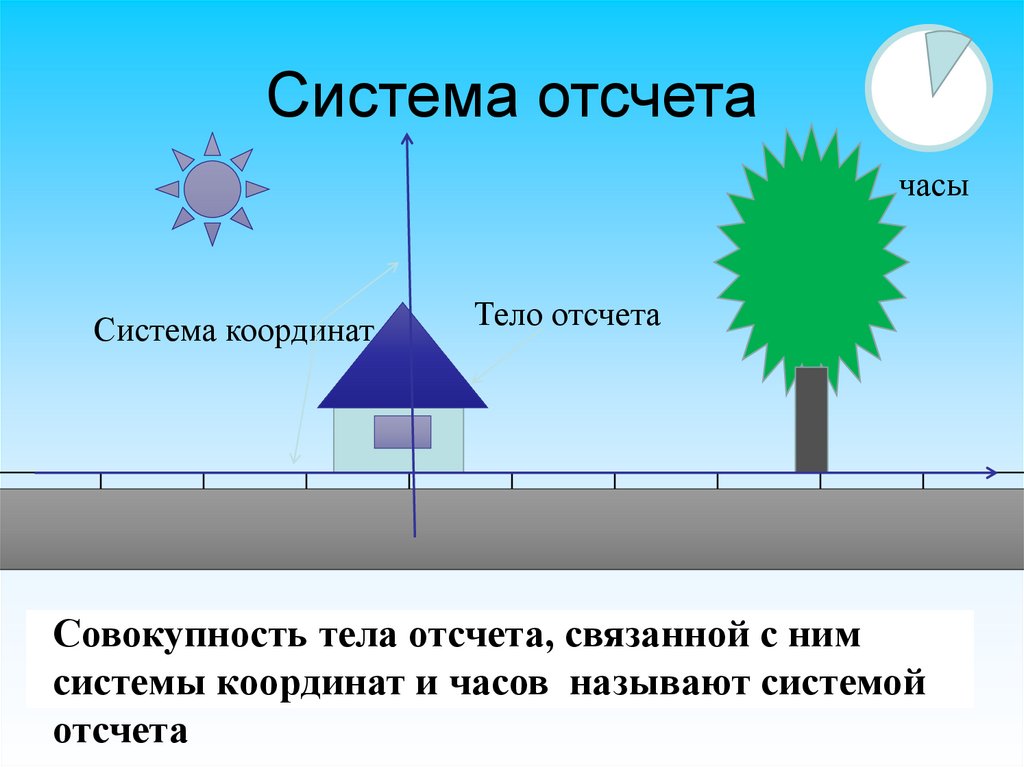
7. Система отчета

Система отчета состоит из тела отсчета,
по отношению к которому описывают
движения тел, связанной с ним системы
координат и часов
Виды систем координат:
Одномерная
Двумерная
Трёхмерная

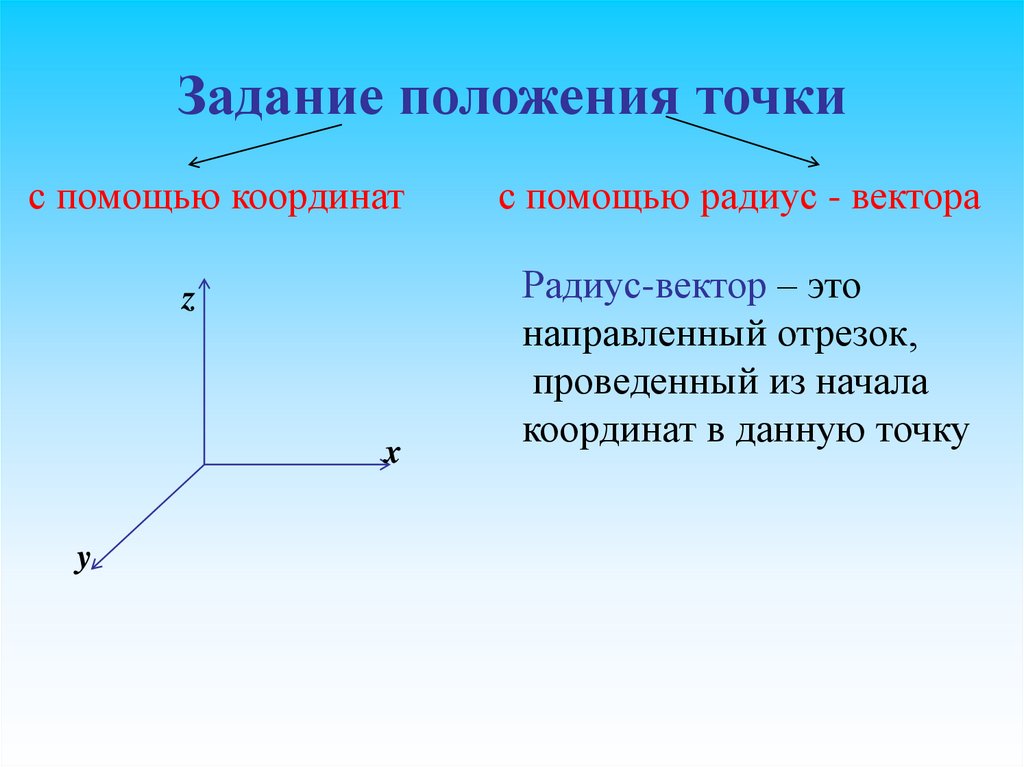
8. Задание положения точки

с помощью координат
z
x
y
с помощью радиус - вектора
Радиус-вектор – это
направленный отрезок,
проведенный из начала
координат в данную точку

9. СЛОЖЕНИЕ ВЕКТОРОВ

Система отсчета
часы
Система координат
Тело отсчета
Совокупность тела отсчета, связанной с ним
системы координат и часов называют системой
отсчета

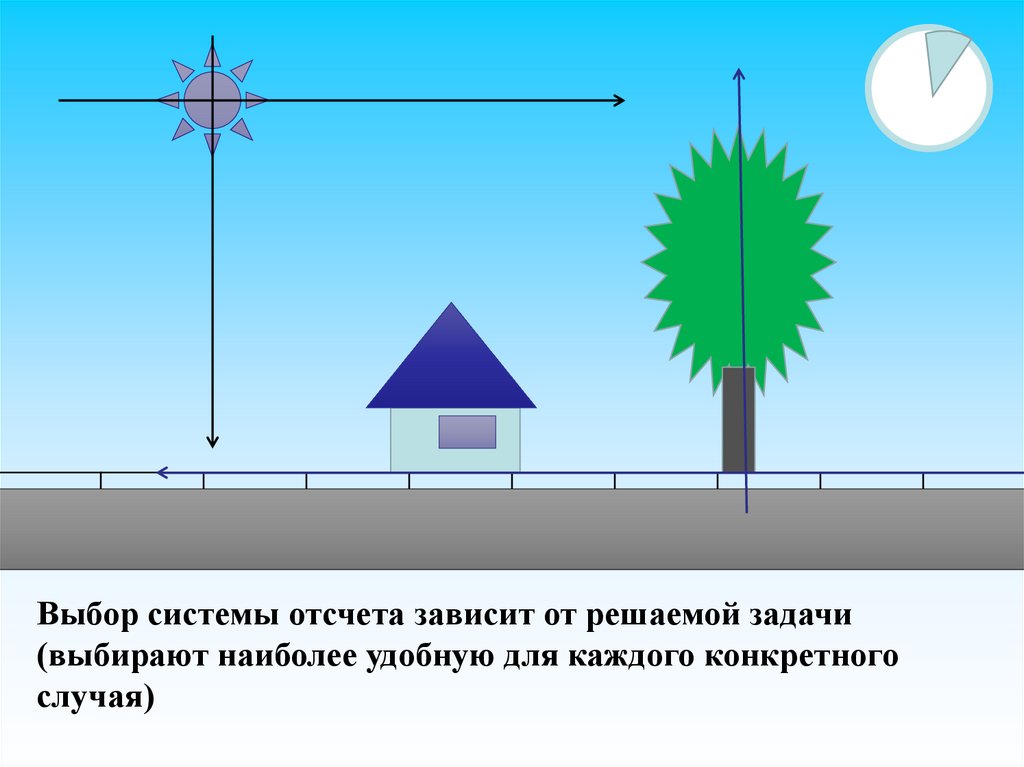
10.

Выбор системы отсчета зависит от решаемой задачи
(выбирают наиболее удобную для каждого конкретного
случая)

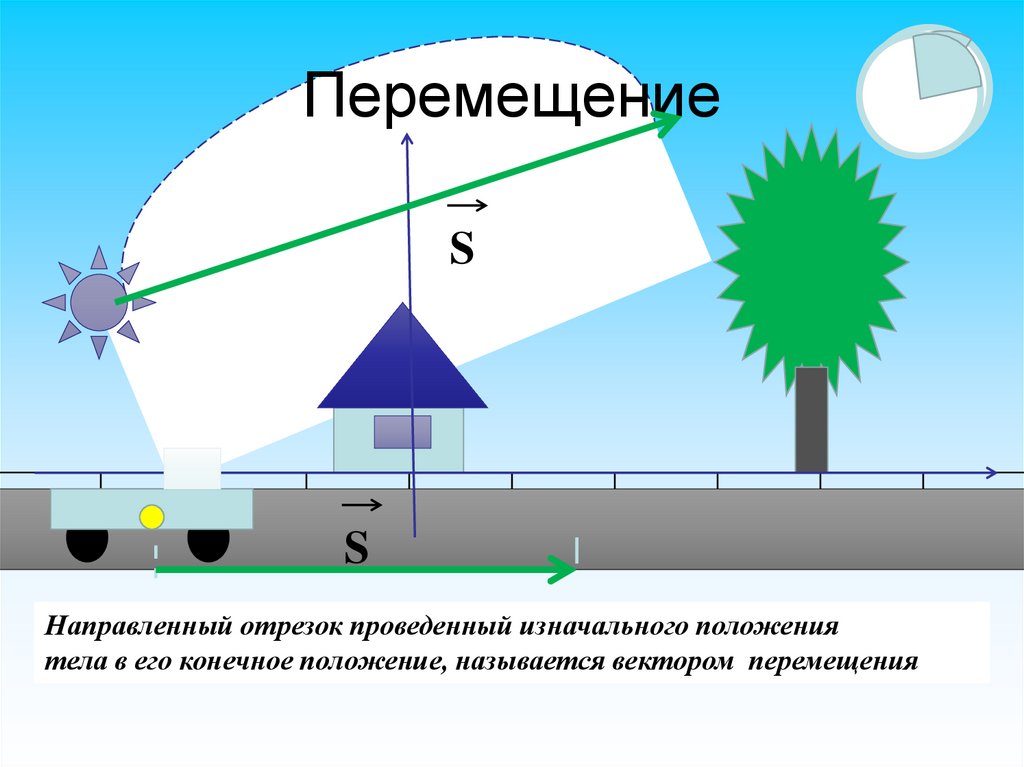
11. СЛОЖЕНИЕ ВЕКТОРОВ

Перемещение
S
S
Направленный отрезок проведенный изначального положения
тела в его конечное положение, называется вектором перемещения

12.

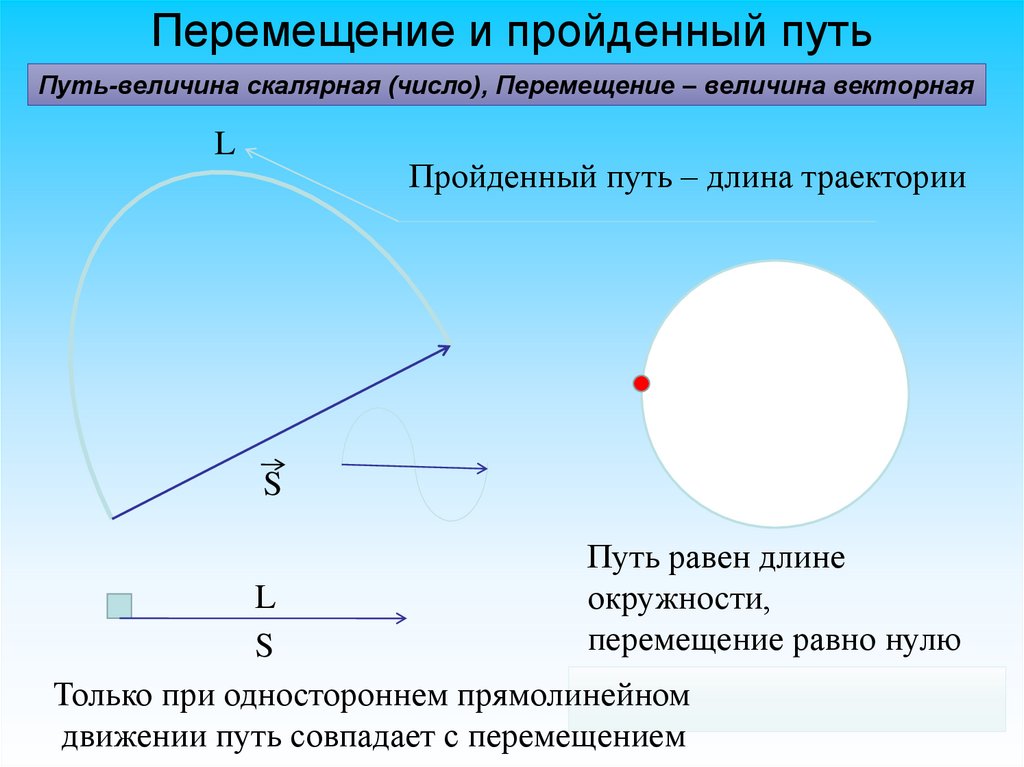
Перемещение и пройденный путь
Путь-величина скалярная (число), Перемещение – величина векторная
L
Пройденный путь – длина траектории
S
Путь равен длине
окружности,
перемещение равно нулю
L
S
Только при одностороннем прямолинейном
движении путь совпадает с перемещением

13. вычитание ВЕКТОРОВ

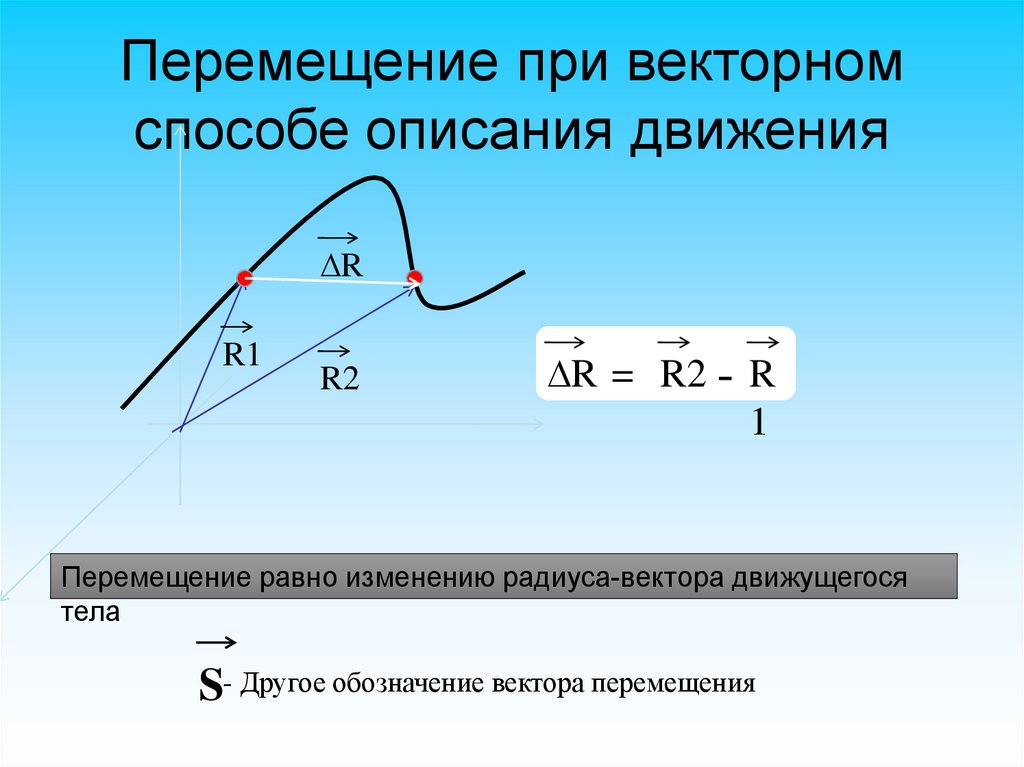
Перемещение при векторном
способе описания движения
∆R
R1
R2
∆R = R2 - R
1
Перемещение равно изменению радиуса-вектора движущегося
тела
S- Другое обозначение вектора перемещения

14.

Перемещение
вектор, соединяющий начальное
положение материальной точки с его
конечным положением.
Траектория
линия, описываемая в пространстве
движущейся материальной точкой.
Путь
длина траектории, по которой
движется тело в течении некоторого
промежутка времени.

15. Положение точки в пространстве

КИНЕМАТИКА
Скорость – это векторная физическая
величина, характеризующая быстроту
движения тела.
Ускорение – это векторная физическая
величина, показывающая быстроту изменения
скорости тела.

16. Вектор и его проекции на ось

Мгновенная скорость
это скорость в каждой конкретной точке
траектории в соответствующий момент
времени.
Средняя скорость
величина, характеризующая движение
тела за весь промежуток времени.

17. КИНЕМАТИКА

ПРОСТЕЙШИЙ ВИД ДВИЖЕНИЯ:
Прямолинейное движение

18. КИНЕМАТИКА

РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ
ДВИЖЕНИЕ
-движение, при котором тело за любые равные
промежутки времени проходит равные пути.
S
S
S
t
t
t

19. КИНЕМАТИКА

Равномерное движение
• Движение, когда за любые равные
промежутки времени тело совершает
одинаковые перемещения. Это
движение с постоянной скоростью.
• Скорость –векторная физическая
величина, равная отношению пути ко
времени, за которое этот путь
пройден.
S
V
t
S Vt
• х = х0+Vхt - уравнение координаты
тела при равномерном движении.

20. КИНЕМАТИКА

Равномерное движение
• (1) – тело движется в сторону
выбранной оси
• (2) - тело движется в противоположную
сторону

21. Система отсчета

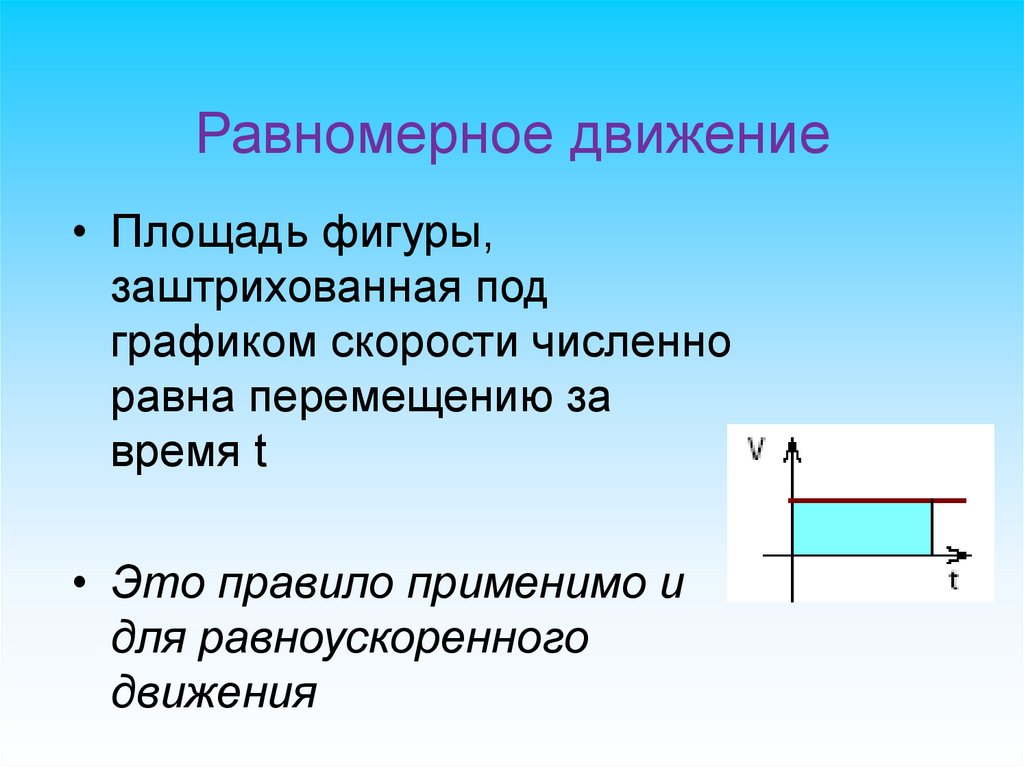
Равномерное движение
• Площадь фигуры,
заштрихованная под
графиком скорости численно
равна перемещению за
время t
• Это правило применимо и
для равноускоренного
движения

22.

КИНЕМАТИКА
Чтобы количественно охарактеризовать это различие
между равномерными движениями, водят физическую
величину – скорость движения.
Скоростью равномерного движения называют
отношение пути, пройденного телом, к промежутку
времени, за который этот путь пройден:
Так как согласно определению равномерного
движения, за двойное, тройное и т. д. время
будут пройдены двойной, тройной и т. д.
пути, за половинное время – половинный
путь и т. д, то значение скорости получится
одно и то же, за какой бы промежуток
времени и на каком бы участке пути ее ни
определять.
Таким образом, при равномерном движении
скорость – постоянная величина,
характеризующая данное движение на
любом участке пути и за любой промежуток
времени: v=const

23. Перемещение

КИНЕМАТИКА
Связь между путем, временем и перемещением в
формуле скорости можно представить в виде
треугольника:
Из треугольника можно
выразить каждую из величин.

24. Перемещение и пройденный путь

Основные свойства скорости
• Скорость величина векторная, то есть
она имеет направление (вектор
скорости совпадает по направлению с
вектором перемещения).
• Скорость равномерного движения
показывает какое перемещение
совершает тело в единицу времени.
• В системе «СИ» скорость измеряется в
(м/с)

25. Перемещение при векторном способе описания движения

КИНЕМАТИКА
При равномерном прямолинейном движении:
Ускорение:
Скорость:
Перемещение:
Пройденный путь:
Координата:

26. Перемещение

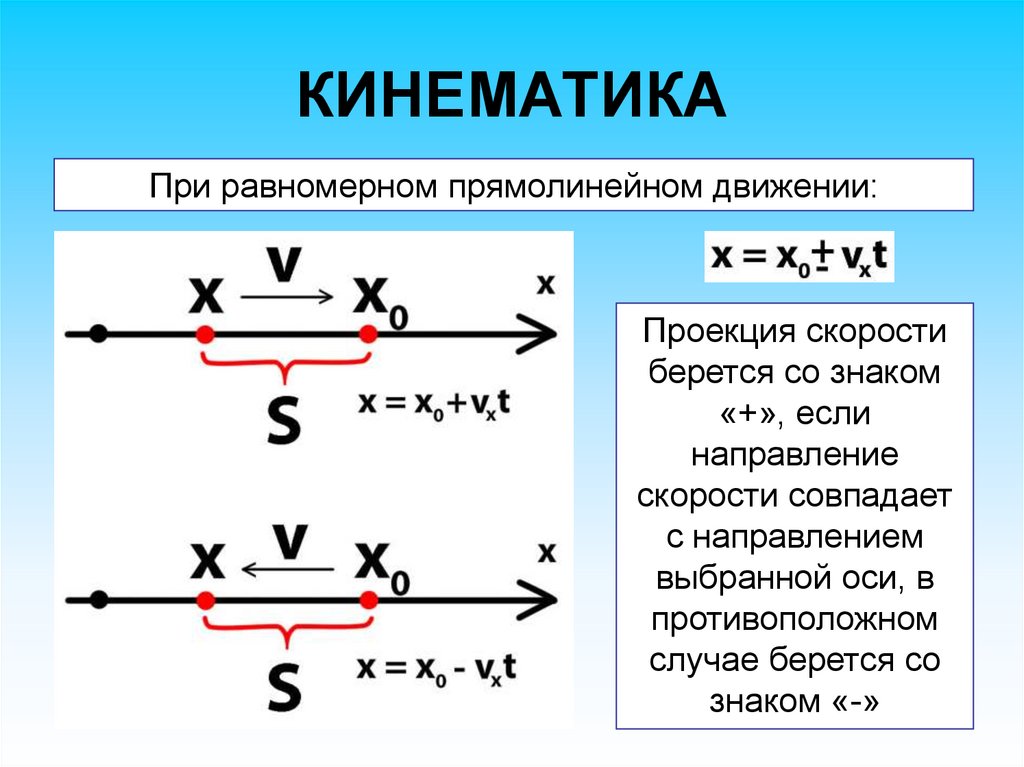
КИНЕМАТИКА
При равномерном прямолинейном движении:
Проекция скорости
берется со знаком
«+», если
направление
скорости совпадает
с направлением
выбранной оси, в
противоположном
случае берется со
знаком «-»

27. КИНЕМАТИКА

НЕРАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ
ДВИЖЕНИЕ:
- движение, при котором тело за любые равные
промежутки времени совершает неодинаковые
перемещения.
Неравномерное движение характеризуется
средней скоростью vср.

28.

КИНЕМАТИКА
РАВНОПЕРЕМЕННОЕ
ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
- движение, при котором модуль
скорости за любые равные
промежутки времени изменяется на
одну и ту же величину

29. КИНЕМАТИКА

РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

30. КИНЕМАТИКА

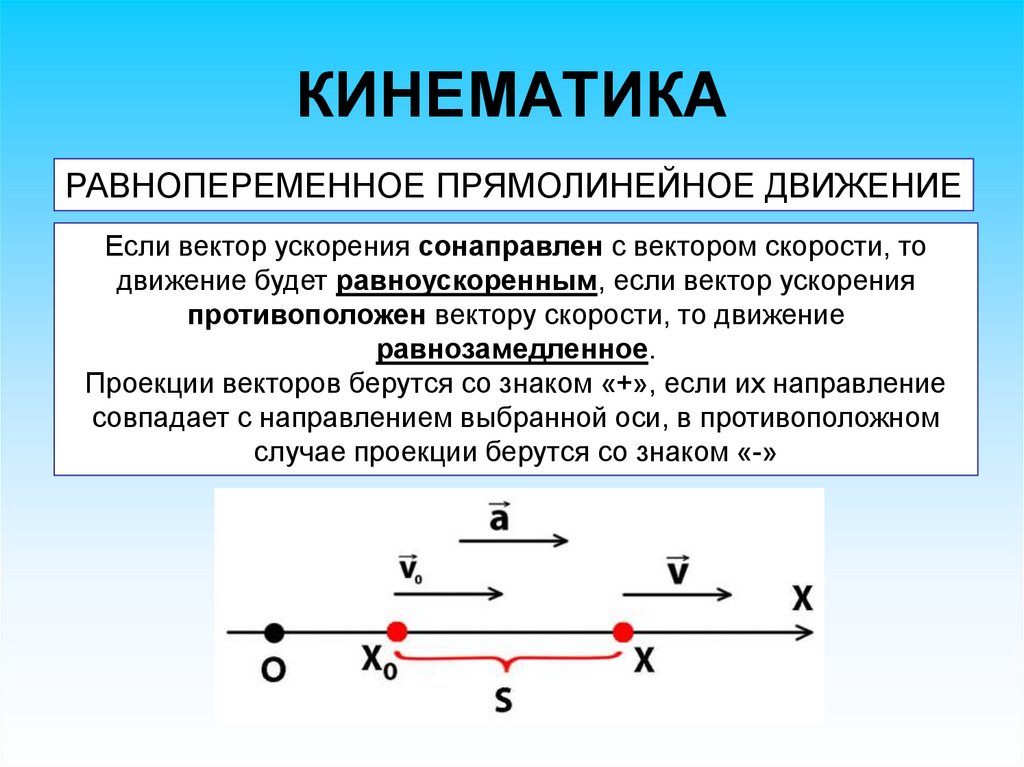
РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
Если вектор ускорения сонаправлен с вектором скорости, то
движение будет равноускоренным, если вектор ускорения
противоположен вектору скорости, то движение
равнозамедленное.
Проекции векторов берутся со знаком «+», если их направление
совпадает с направлением выбранной оси, в противоположном
случае проекции берутся со знаком «-»

31. Равномерное движение

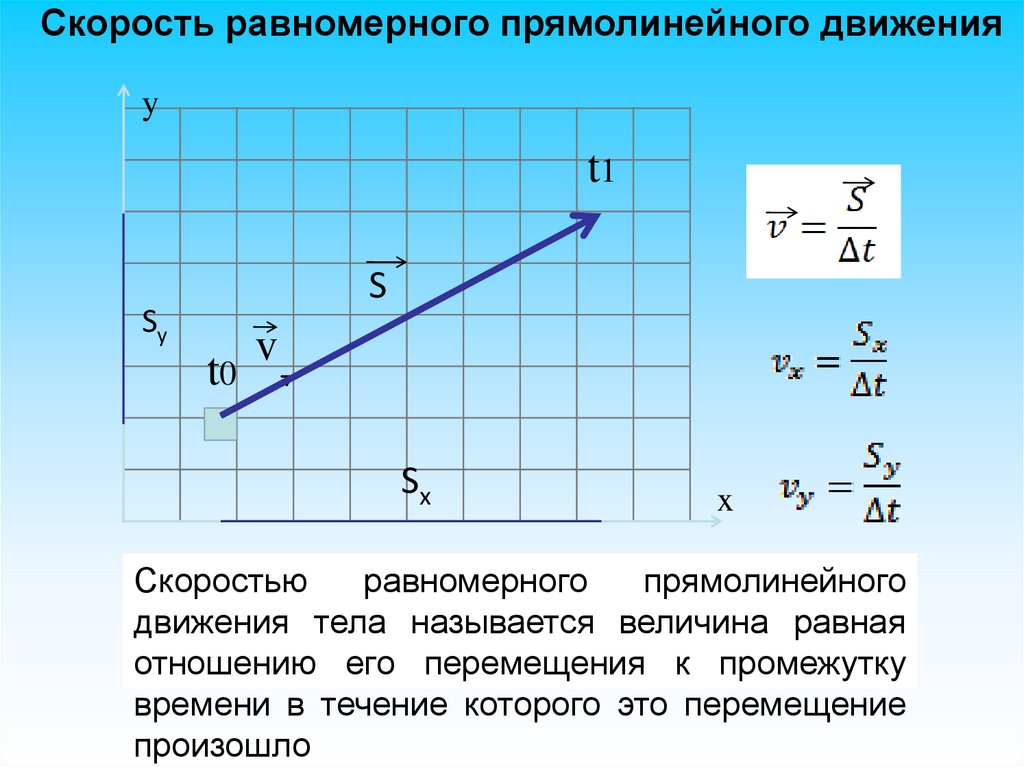
Скорость равномерного прямолинейного движения
y
t1
S
Sy
t0
v
Sx
x
Скоростью
равномерного
прямолинейного
движения тела называется величина равная
отношению его перемещения к промежутку
времени в течение которого это перемещение
произошло

32. Равномерное движение

S= vt
Sx = vx t
Sy = vy t
Перемещение тела при равномерном прямолинейном
движении равно произведению скорости тела на
время его движения

33. Равномерное движение

Основные свойства скорости
• Скорость величина векторная, то
есть она имеет направление
(вектор скорости совпадает по
направлению с вектором
перемещения).
• Скорость равномерного движения
показывает какое перемещение
совершает тело в единицу
времени.
• В системе «СИ» скорость
измеряется в (м/с)

34. КИНЕМАТИКА

Движение, при котором тело за любые равные
промежутки времени совершает одинаковые
перемещения. называют ПРЯМОЛИНЕЙНЫМ
РАВНОМЕРНЫМ.
s
v
t
скорость равномерного движения –
[м/с]
Движение, при котором за равные промежутки
времени тело совершает неравные перемещения
называют неравномерным или переменным.
скорость неравномерного движения:
Направление скорости при:
прямолинейном движении –
неизменно
криволинейном движении – по
касательной к траектории в
данной точке
v2
v1
v
v3
s
vср
Δt
vv
4

35. КИНЕМАТИКА

Ускорение - величина, характеризующая изменение
скорости
при
неравномерном
движении
тела.
Средним ускорением неравномерного движения в
интервале от t до t + ∆t называется векторная величина,
равная отношению изменения скорости ∆v к интервалу
времени ∆t:
Δv
a
Δt
При свободном падении вблизи поверхности Земли
где
g 9,8 м
с
2
a g

36. Основные свойства скорости

Неравномерное движение
• Средняя скорость
S (весь)
Vср
t всё
S1 S 2 ... s n
Vср
t1 t 2 ... t n
• Мгновенная скорость
Vмгн
S
; t 0
t
• Физический смысл производной: Производная
перемещения (координаты) – есть скорость.
S´=V,
Производная скорости – есть ускорение.
V´=a

37. КИНЕМАТИКА

Равноускоренное движение
• Движение, когда за любые равные
промежутки времени скорость тела
изменяется одинаково. Это движение с
постоянным ускорением.
• Ускорение – векторная физическая
величина, равная отношению изменения
скорости к промежутку времени, за
которое это изменение произошло.
V - V0
а
t
V
a
t
V V0 at

38. КИНЕМАТИКА

Равноускоренное движение
at 2
2
• х = х0+Vхt+
- уравнение координаты
тела при равноускоренном движении.
• Перемещение при равноускоренном
движении:
at 2
V V
S V0 t
2
S
2
2
0
2a
• Если V0=0 и за первую секунду тело
проходит путь S1, то S1: S2: S3= 1:3:5 …

39. КИНЕМАТИКА

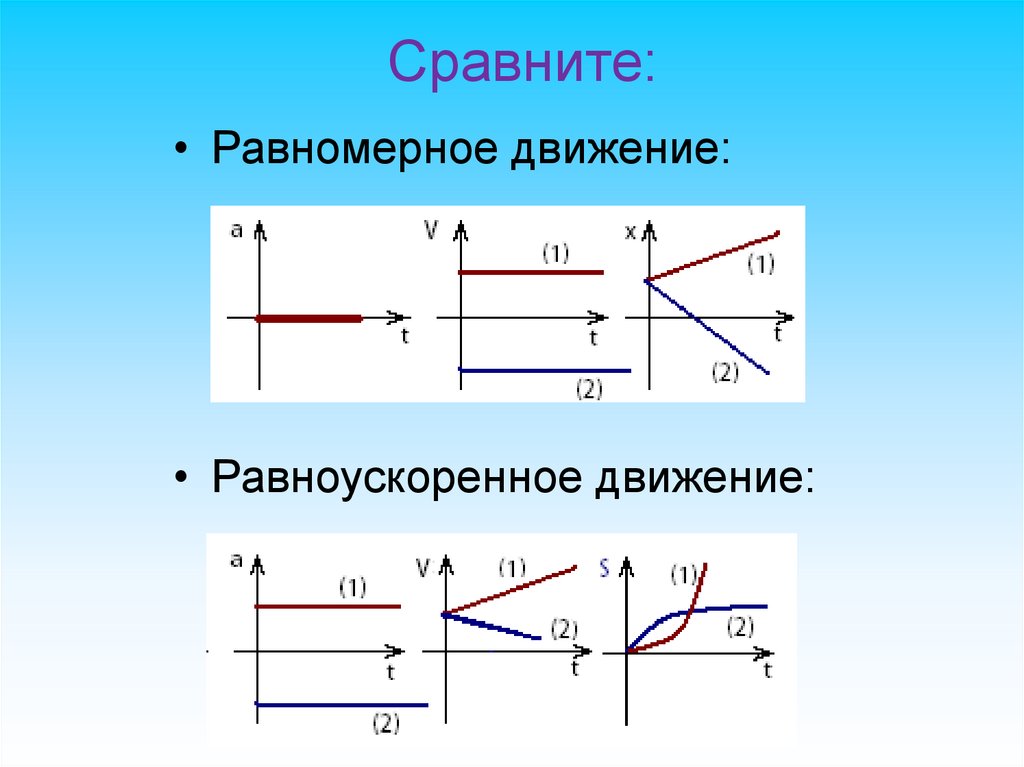
Равноускоренное движение
• (1) – тело набирает скорость,
• (2) - тело тормозит.

40. КИНЕМАТИКА

Сравните:
• Равномерное движение:
• Равноускоренное движение:

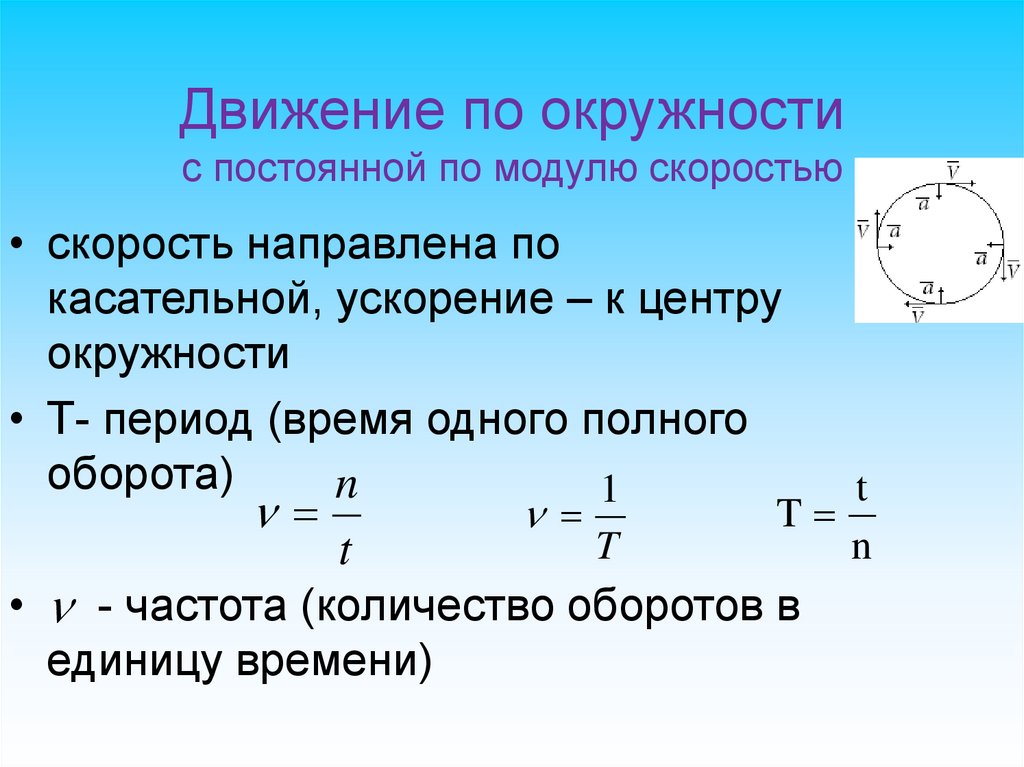
41. КИНЕМАТИКА

Движение по окружности
с постоянной по модулю скоростью
• скорость направлена по
касательной, ускорение – к центру
окружности
• Т- период (время одного полного
оборота)
n
t
1
T
n
T
t
• - частота (количество оборотов в
единицу времени)

42. КИНЕМАТИКА

Движение по окружности
с постоянной по модулю скоростью
• Длина окружности
l 2 R
• Скорость при движении по
окружности
2 R
V
T
- угловая скорость,
2
2
показывает, на какой угол
t
T
поворачивается тело за 1с.

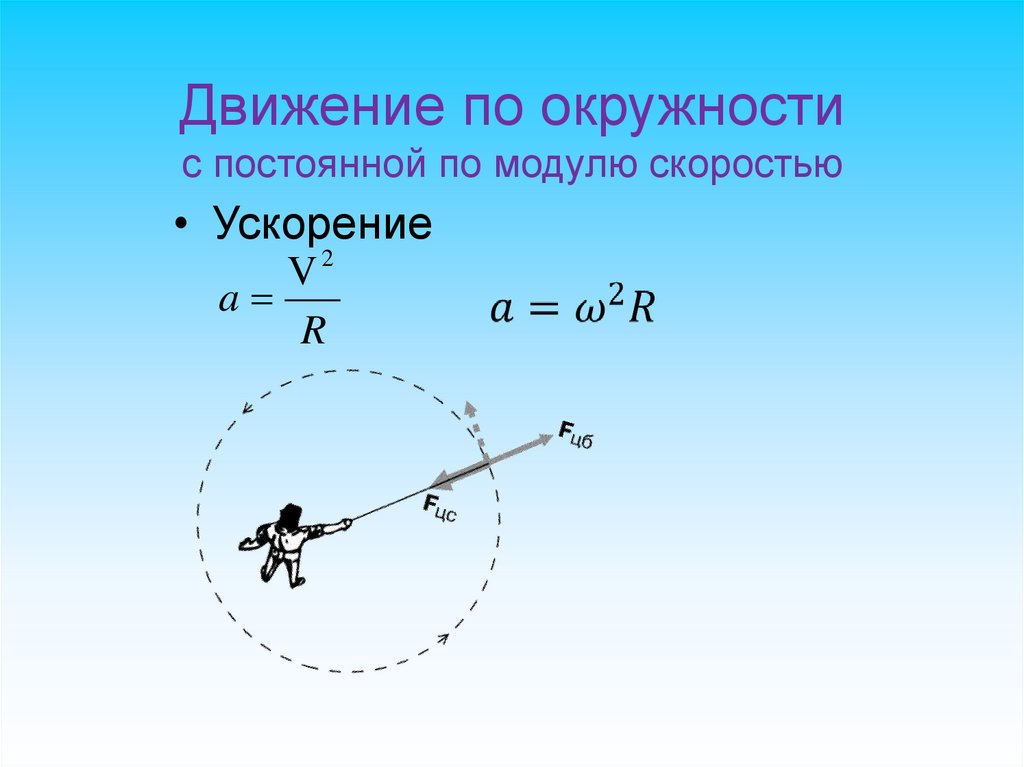
43. Скорость равномерного прямолинейного движения

Движение по окружности
с постоянной по модулю скоростью
• Ускорение
2
V
a
R

44.

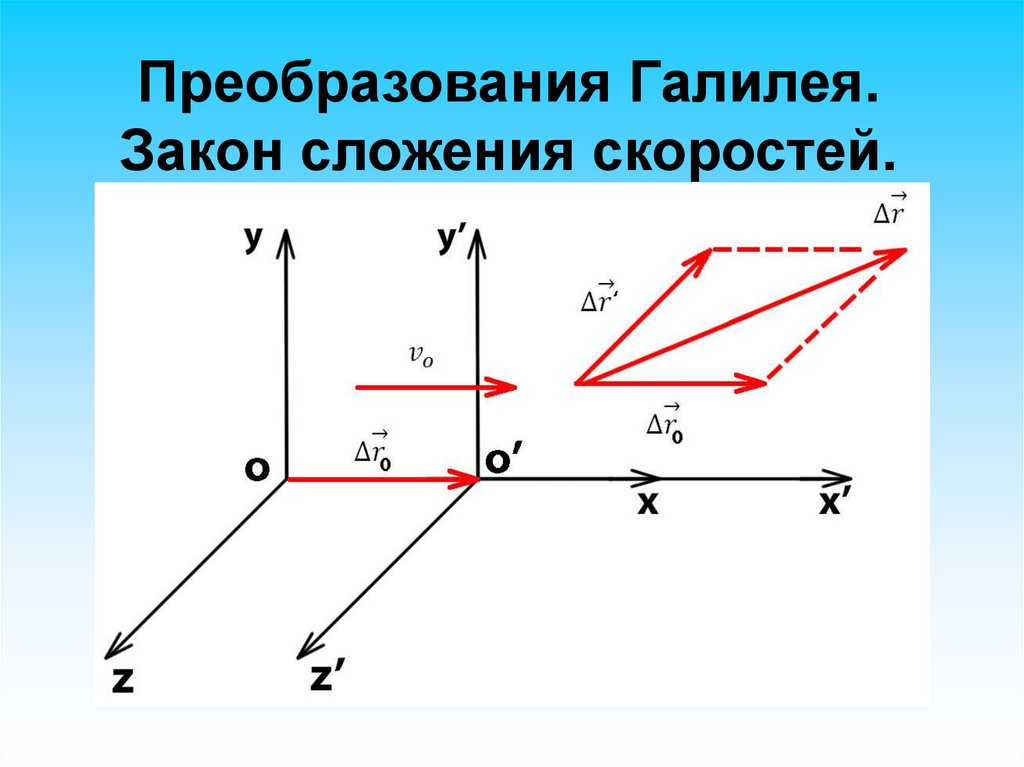
45. Основные свойства скорости

Преобразования Галилея.
Закон сложения скоростей.
Позволяют связать между собой координаты некоторой
материальной точки в двух разных инерциальных системах
отсчета при относительно небольших скоростях движения.
Инерциальной системой отсчета называется система отсчета, в
которой тело, свободное от внешних воздействий покоится или
движется равномерно и прямолинейно.
Преобразования Галилея удовлетворяют принципу
относительности:
любая из инерциальных систем отсчета может быть принята за
неподвижную, а преобразования координат в этой системе отсчета
задаются преобразованиями Галилея с учетом знака скорости
движения системы отсчета.

46.

Преобразования Галилея.
Закон сложения скоростей.

47.

Преобразования Галилея.
Закон сложения скоростей.
Перемещение тела за данный промежуток времени
относительно неподвижной системы отсчета равно
геометрической (векторной) сумме его перемещения
относительно неподвижной системы отсчета и
перемещения подвижной системы отсчета
относительно неподвижной за этот промежуток
времени:
Скорость тела v относительно неподвижной
системы отсчета равна геометрической
сумме его скорости v’ относительно
подвижной системы отсчета и скорости v0
подвижной системы отсчета относительно
неподвижной

48. Неравномерное движение

Преобразования Галилея.
Закон сложения скоростей.
КЛАССИЧЕСКИЙ ЗАКОН СЛОЖЕНИЯ
СКОРОСТЕЙ:

49. Равноускоренное движение

КИНЕМАТИКА
РЕШИТЬ ЗАДАЧУ:
1. Автомобиль прошел первую половину пути со скоростью 10 м/с,
а вторую половину пути – со скоростью 15 м/с. Найти среднюю
скорость.
2. Велосипедист проехал за 5 секунд 40 метров, за следующие 10
секунд 100 метров, и за последующие 5 секунд 60 метров. Найти
среднюю скорость прохождения всего пути.
3. Автомобиль прошел расстояние от пункта А до пункта B со
скоростью v1 = 80 км/ч и обратно со скоростью v2 = 40 км/ч. Найти
среднюю скорость автомобиля.

50. Равноускоренное движение

Кинематика твердого тела
Простейшие движения твердого тела
• Поступательное движение
• Вращение вокруг неподвижной оси
(вращательное)

51. Равноускоренное движение

Поступательное движение
Поступательное движение твердого тела – это
такое движение, при котором любая прямая,
проведенная в теле, перемещается параллельно
самой себе.
А
VA
С
VÑ
В
VB
V

52. Сравните:

Поступательное движение
VA Vc VB
aA aC aB
При поступательном движении все точки тела
описывают одинаковые траектории и имеют в
каждый момент времени одинаковые по модулю и
направлению скорости и ускорения.

53. Движение по окружности с постоянной по модулю скоростью

Вращательное движение
Вращательное движение твердого тела
• Вращательное движение твердого тела – это
такое движение, при котором две точки тела
остаются неподвижными.
• Проходящая через эти точки прямая называется
осью вращения.

54.

Вращательное движение
Положение тела при вращательном движении
однозначно определяется углом поворота φ
Закон вращательного движения:
(t )

55. Движение по окружности с постоянной по модулю скоростью

Вращательное движение
•Основные кинематические характеристики
вращательного движения:
Угловая скорость ω [рад/c]
Угловое ускорение ε [рад/c2]
Z
z
z

56.

Вращательное движение
d
dt
d
dt
Вектор угловой скорости лежит на оси вращения и
направлен в сторону, откуда видно, что тело
вращается против хода часовой стрелки.

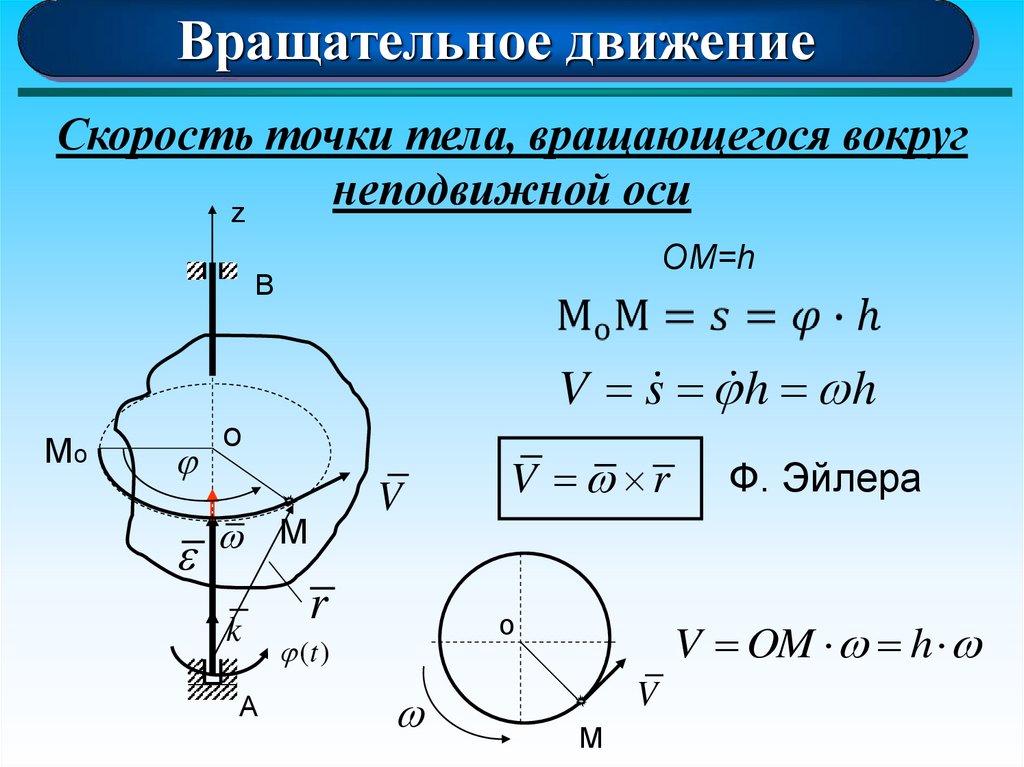
57. Преобразования Галилея. Закон сложения скоростей.

Вращательное движение
Скорость точки тела, вращающегося вокруг
неподвижной оси
z
ОМ=h
B
V s h h
Мо
о
V
М
k
A
r
V r
о
(t )
Ф. Эйлера
V OM h
V
М

58. Преобразования Галилея. Закон сложения скоростей.

Вращательное движение
Ускорение точки тела, вращающегося вокруг
неподвижной оси
a a an
a V R
a
О
a
an
R
V
an
2 R
R
R
2
2
М
V
a a a R
2
n
2
4
2

59. Преобразования Галилея. Закон сложения скоростей.

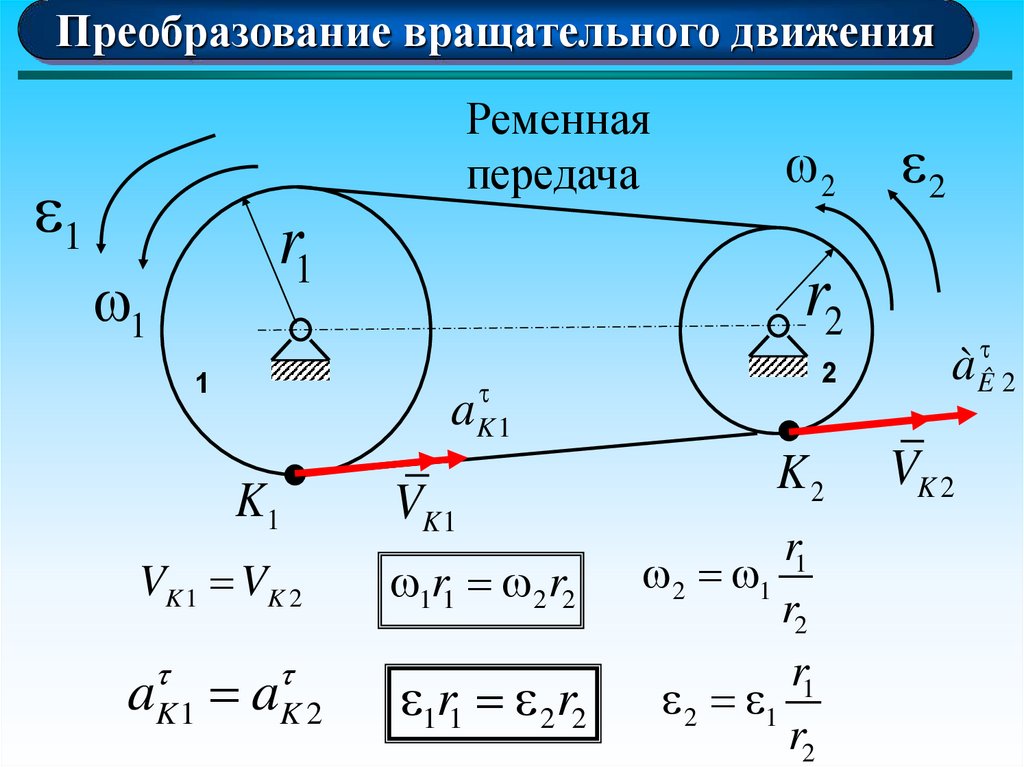
Преобразование вращательного движения
1
Ременная
передача
r1
1
1
VK 1 VK 2
aK 1 aK 2
2
r2
a
K1
2
2
K1
VK 1
1r1 2 r2
1r1 2 r2
K2
r1
2 1
r2
r1
2 1
r2
à
VK 2
Ê2

60. Преобразования Галилея. Закон сложения скоростей.

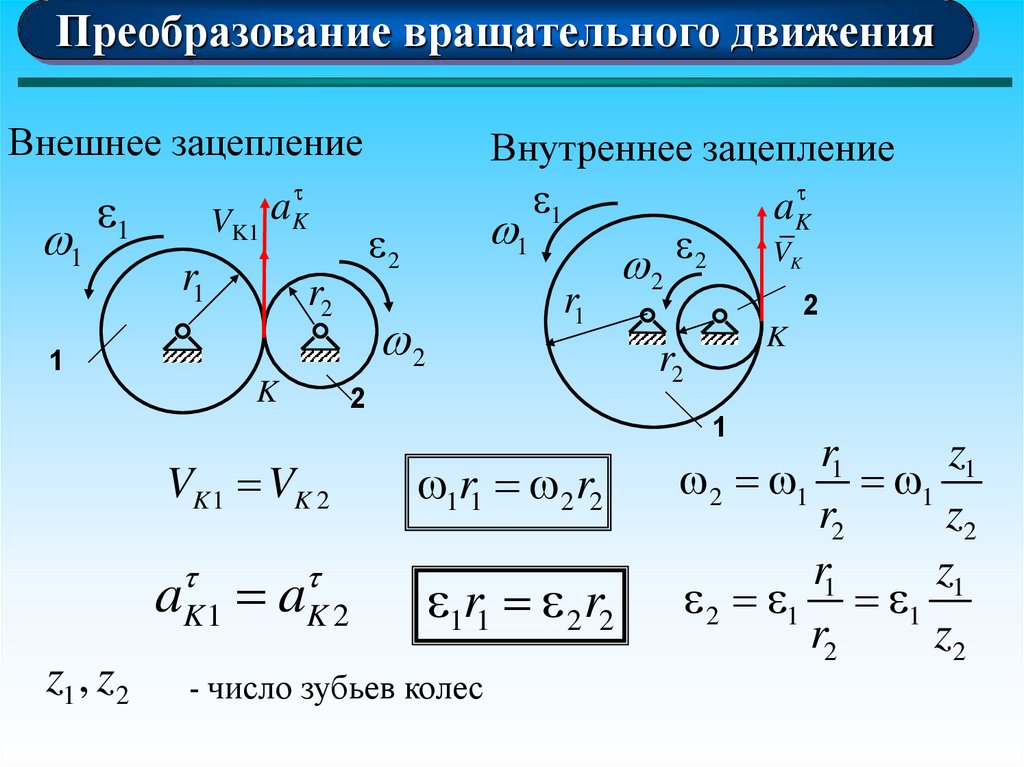
Преобразование вращательного движения
Внешнее зацепление
1
a
VK1 K
1
r1
Внутреннее зацепление
1
aK
1
2
VK
2
r1
2
K
r2
2
r2
2
1
K
2
1
VK 1 VK 2
aK 1 aK 2
z1 , z2
1r1 2 r2
1r1 2 r2
- число зубьев колес
r1
z1
2 1 1
r2
z2
r1
z1
2 1 1
r2
z2

61. КИНЕМАТИКА

Сложное движение точки
Сложное движение точки
Сложное движение точки - такое движение,
которое может быть составлено из двух
(нескольких) простых.
Движение рассматривается в двух системах
отсчета: основной (неподвижной) и движущейся.

62. Простейшие движения твердого тела

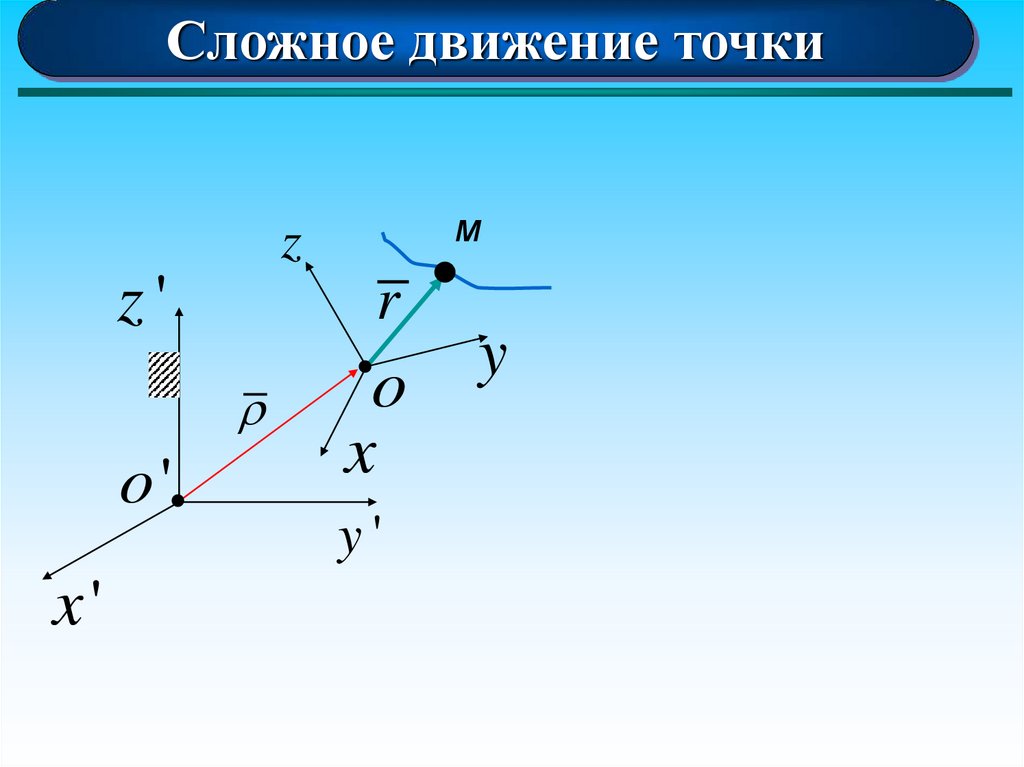
Сложное движение точки
м
z
z'
r
o'
x'
o
x
y'
y

63.

Сложное движение точки
Движение
точки
относительно
основной
(неподвижной) системы отсчета называется
абсолютным.
Движение точки относительно подвижной
системы отсчета называется относительным.
Движение подвижной системы отсчета (и
неизменно связанных с ней точек пространства)
называется переносным.

64.

Сложное движение точки
Абсолютная скорость точки - скорость
относительно неподвижной системы отсчета.
Относительная скорость точки - скорость
относительно подвижной системы отсчета
Скорость неизменно связанной с подвижными
осями точки, с которой в данный момент
совпадает
движущаяся
точка,
называется
переносной скоростью.

65.

Сложное движение точки
Теорема о сложении скоростей:
V Vотн Vпер
Абсолютная скорость точки равна геометрической
сумме переносной и относительной скоростей

66. Закон вращательного движения:

Сложное движение точки
Скорости и ускорения при сложном движении
обозначаются
Va ,
aa - абсолютные
Vr ,
ar - относительные
Ve ,
ae - переносные
Сложение векторов скорости по теореме косинусов
Va
Ve
Vr
Va Vr Ve
Va Vr2 Ve2 2VrVe cos

67.

Сложное движение точки
Теорема Кориолиса
a aотн апер аКор
Абсолютное
ускорение
точки
равно
геометрической сумме переносного ускорения,
относительного ускорения и ускорения Кориолиса

68.

Сложное движение точки
Ускорение Кориолиса характеризует изменение
относительной скорости точки в переносном
движении и переносной скорости точки в
относительном движении.
Кориолисово ускорение равно удвоенному
векторному произведению переносной угловой
скорости на относительную скорость точки
aКор 2 пер Vотн

69.

Сложное движение точки
В численном виде, ускорение кориолиса равно
ak 2 Vr sin( ^ Vr )
Правило Н. Е. Жуковского
Чтобы найти направление вектора ускорения
Кориолиса, необходимо спроецировать вектор
относительной
скорости
на
плоскость,
перпендикулярную , и повернуть эту проекцию на
90 в сторону переносного вращения.

70.

Сложное движение точки
z
90
Vr
90
ak
ak
y
Vr
'
Vr
x
ak 2 Vr sin
ak 2 Vr

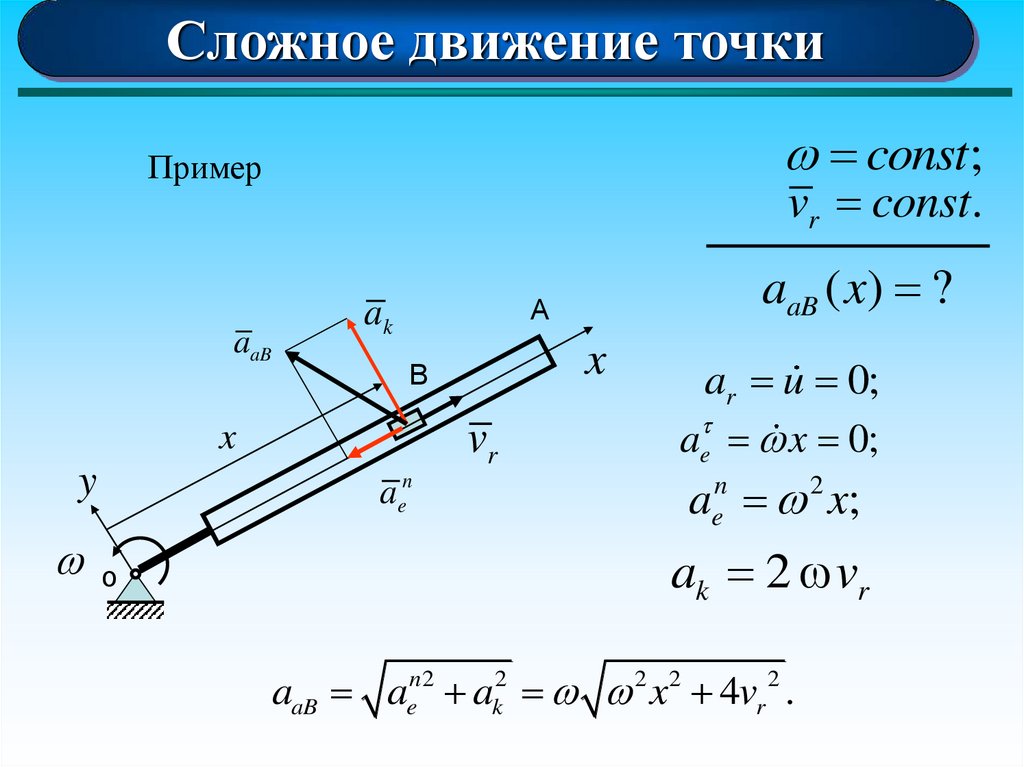
71.

Сложное движение точки
const;
Пример
aaB
vr const.
ak
vr
aen
о
x
В
x
y
aaB ( x) ?
А
ar u 0;
ae x 0;
a x;
n
e
2
ak 2 vr
aaB aen 2 ak2 2 x2 4vr 2 .

72.

Плоское движение твердого тела
Плоскопараллельным (плоским) движением твердого
тела называется такое движение, при котором все точки
тела перемещаются в параллельных плоскостях
z
y
O
c
x
Vc
y
c
c
o
Рис.3.
Vc
x
Плоскопараллельное движение твердого тела слагается
из поступательного движения, при котором все точки
тела движутся как полюс С и из вращательного
движения вокруг этого полюса

73.

Плоское движение твердого тела
Уравнения движения плоской фигуры
y
xc
yc f 2 (t );
c
o
xc f1 (t );
A
f3 (t ).
yc
Рис.2.
x

74.

Плоское движение твердого тела
Скорость точки при плоском движении тела
VB VA VBA
VB
А
VA VBÀ
В
VA
VBA AB
VBA AB
Скорость какой-либо точки В плоской фигуры равна
геометрической сумме скорости полюса А и скорости
точки В при вращении фигуры вокруг полюса А.

75.

Плоское движение твердого тела
Мгновенный центр скоростей
Мгновенным центром скоростей (МЦС) называется
точка плоской фигуры, скорость которой в данный
момент равна нулю.
VB
B
A
VC
VA
P
VA VP VAP ;
0
VA VAP PA.
C
VA VB VC
AP BP CP

76. Абсолютная скорость точки - скорость относительно неподвижной системы отсчета. Относительная скорость точки - скорость

Плоское движение твердого тела
Свойства МЦС:
•Скорости всех точек фигуры перпендикулярны отрезкам,
соединяющим эти точки с МЦС
•Модули скоростей пропорциональны расстояниям точек
до МЦС
•Угловая скорость тела равна в каждый данный момент
времени отношению скорости какой-нибудь точки к ее
расстоянию до МЦС

77. Теорема о сложении скоростей:

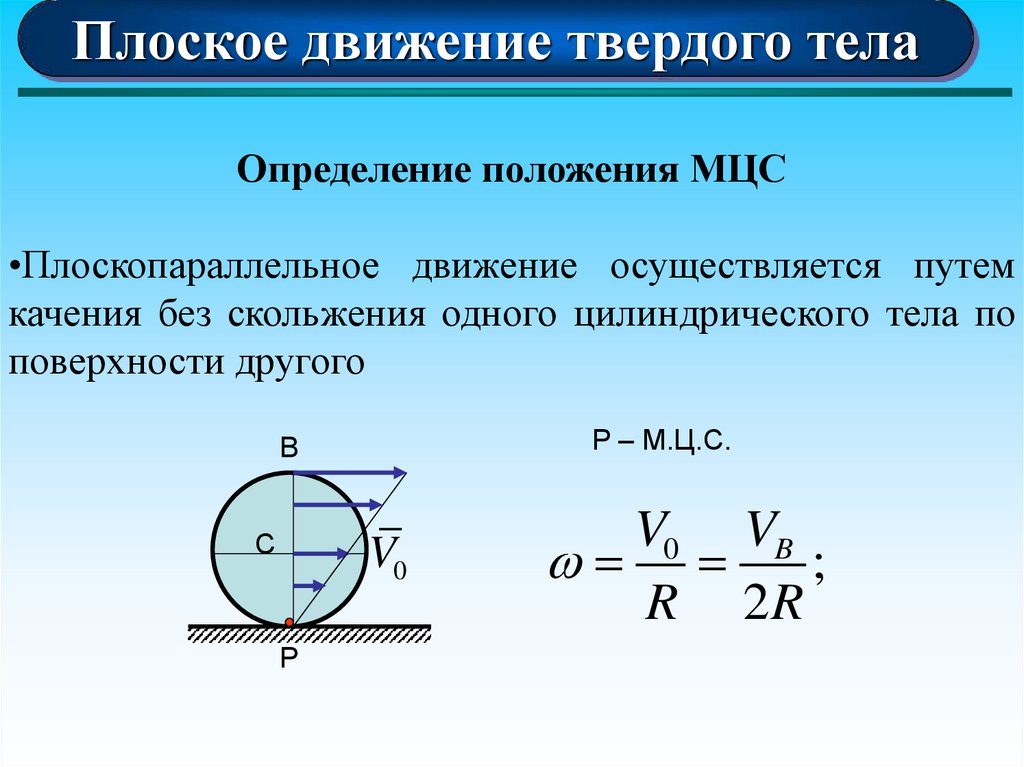
Плоское движение твердого тела
Определение положения МЦС
•Плоскопараллельное движение осуществляется путем
качения без скольжения одного цилиндрического тела по
поверхности другого
P – M.Ц.С.
B
C
V0
P
V0 VB
;
R 2R

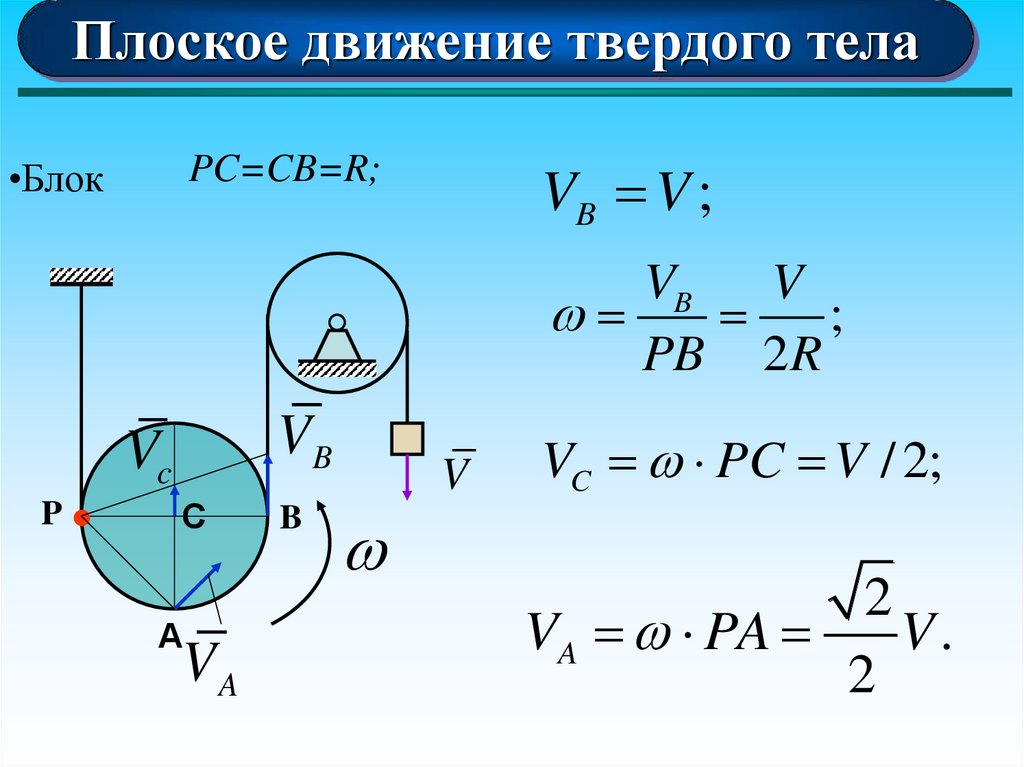
78.

Плоское движение твердого тела
VB V ;
PC=CB=R;
•Блок
VB
V
;
PB 2R
VB
Vc
P
С
A
VA
B
V
VC PC V / 2;
2
VA PA
V.
2

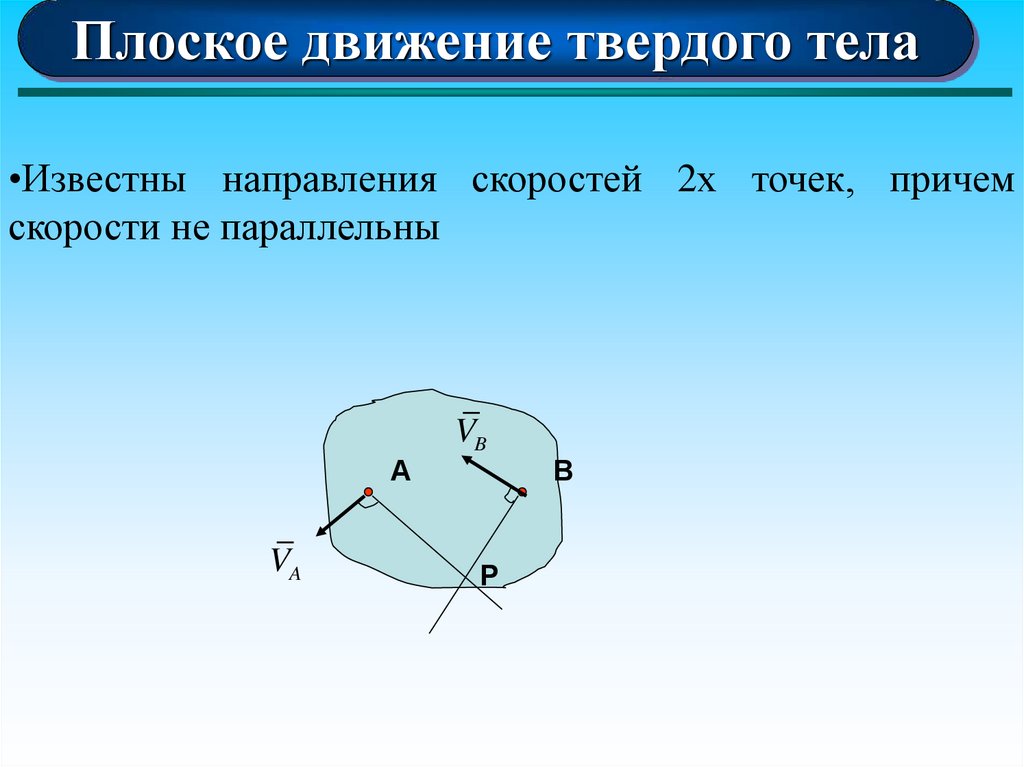
79. Теорема Кориолиса

Плоское движение твердого тела
•Известны направления скоростей 2х точек, причем
скорости не параллельны
А
VA
VB
Р
В

80.

Плоское движение твердого тела
•Скорости двух точек тела параллельны, не равны между
собой и перпендикулярны прямой, соединяющей эти
точки
BP x
VA
VA
VB
.
AB x x
VB
А
В
х
Р